{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"<a id=\"top\"></a>\n",
"# **3.1 Nonlinear bond - softening and hardening**\n",
"\n",
"[](https://moodle.rwth-aachen.de/mod/page/view.php?id=551816) part 1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/start_flag.png\" alt=\"Previous trip\" width=\"40\" height=\"40\">\n",
" <b>Starting point</b> </div> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"By saying that we want to capture the _material behavior_ we mean\n",
"that we realistically describe the **constitutive relation** between the strain and stress which is **valid for\n",
"any material point** of the considered volume. With the focus on a one-dimensional interface between two material\n",
"components we can reduce this task to the relation between bond stress and slip.\n",
"In Tour 2, we assumed the constitutive bond-slip relation constant. However, as we have learned\n",
"in trip [2.1 Pull-out of elastic fiber from rigid matrix](../pull_out/2_1_1_PO_observation.ipynb)\n",
"this stick-slip interface behavior cannot realistically describe the experimentally measured\n",
"response of steel-concrete pull-out with varied length of the bond length $L_b$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/destination.png\" alt=\"Previous trip\" width=\"40\" height=\"40\">\n",
" <b>Where are we heading</b> </div> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To improve the quality of the model, in this notebook we introduce and investigate more complex shapes of bond slip laws and their effect on the observed pullout response. This extension will enable a more **realistic \n",
"prediction of a wide range of pull-out and crack bridge tests**, including \n",
"steel rebars, carbon textile fabrics or carbon fiber reinforced polymer (CFRP) sheets.\n",
"Using the models, we will perform automated studies of the pull-out response that can demonstrate the different phenomenology behind hardening and softening constitutive behavior.\n",
"These studies indicate how validated models can support the definition of engineering design rules. "
]
},
{
"attachments": {
"9086d2ee-b436-406a-aae8-44f90e71f5b3.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1AAAAEcCAYAAADJHlUPAAAABHNCSVQICAgIfAhkiAAAABl0RVh0U29mdHdhcmUAZ25vbWUtc2NyZWVuc2hvdO8Dvz4AAAAqdEVYdENyZWF0aW9uIFRpbWUARnIgMzAgQXByIDIwMjEgMTc6NTc6MzYgQ0VTVHJHkO0AACAASURBVHic7N15dFT3fffx99zZN82i0b4LIQlJ7GDMYqgNlMUmLia266WpszTJk+a06XOSrmlzntMkbZrnOe0faZrHfeI43u3YxjbBWAdjMGbfESCBhNC+bzOj2Wfuvc8fF42RwTbYLAZ+r3M4gHTnbnM1up/7+/2+P52qqiqCIAiCIAiCIAjCp5Ju9A4IgiAIgiAIgiDcLESAEgRBEARBEARBuEwiQAmCIAiCIAiCIFwmEaAEQRAEQRAEQRAukwhQgiAIgiAIgiAIl0kEKEEQBEEQBEEQhMskApQgCIIgCIIgCMJlEgFKEARBEARBEAThMokAJQiCIAiCIAiCcJlEgBIEQRAEQRAEQbhMIkAJgiAIgiAIgiBcJhGgBEEQBEEQBEEQLpMIUIIgCIIgCIIgCJdJBChBEARBEARBEITLJAKUIAiCIAiCIAjCZRIBShAEQRAEQRAE4TKJACUIgiAIgiAIgnCZDDd6BwRBEARBEG5WqVSKsbExxsfHycnJwW63X7NtDQ4O0tXVxejoKMlkEpvNxuLFizEajddsm180qVSKjo4OOjs7qaiooKioiEQigd/vZ3x8nPz8fKxWa3r5ZDKZXr6qqoqCgoIbuPfCrUK0QAmCIAiCIHxG4XCYffv28cwzz9DZ2XlNtqGqKrIss23bNv7lX/6F7373u3znO9/hRz/6EbFY7Jps84sqFovx5ptv8t3vfpf33nsPAL/fzwcffMBTTz3F4ODgpOXD4TCvv/463/nOd/jggw9uxC4LtyDRAiUIgiAIgvAZhcNh9u7dy0svvcTChQuZNm3aVd+GoiiMjIzwq1/9CoPBwLe//W3mzp2Lw+GY1NpyO9DpdHg8HkpLS3E6nQAEAgF27drFSy+9xPr16ykpKUkvL0kSXq930vKC8HmJACUIgiAIgvA5KIpCKpVCVdVrsn5Zlunp6SEYDLJs2TKWL19OeXk5er0evV5/Tbb5RSPLMoqiYLFYuO+++1i8eDFZWVnp73/ce2C327n//vtZunQp2dnZ13u3r6pkMokkSbfNe/5FplOv1U+7IAiCIAi3pEQiQX9/P9u3b6e1tZWRkREAfD4f1dXVrFy5ErfbjcGgPacdHh6mvr6eY8eOsW7dOoaGhjh48CCBQACfz8eqVauYMWMG/f397Nmzh4aGBuLxOMXFxaxbt47y8nIsFsukfWhtbWXPnj2cOHECv9+PxWKhtLSUlStXMmXKFGw2G6C1Tvzud79jYGCAdevWMWPGjEnr+fWvf00gEGDhwoUsXLiQQCDAli1bOHbsGMuWLSMSiXDw4EH8fj8ul4uFCxeyaNEisrOzaWtrY+PGjfzmN7/h3LlzLF68mIKCAkwmE9XV1fzVX/3VJ57HtrY29u7dS0NDA6Ojo5hMJkpLS1mxYgUVFRU4HA56enrYuHEj7777Ljt37qSoqIiqqiqKiopYsmQJ9957LyaT6ZLrHxwc5MCBAzQ0NDAwMEAsFiMjI4PKykqWLl1KeXn5pPFTY2Nj7N69m6NHj9Lf308ymcRut1NQUMDatWuZOnUqvb29bNu2jRMnTvDAAw9w8uRJzpw5QzweJycnh8WLF7N48eL0+QeIx+P09PTw7rvv0tLSwvj4OFarlaqqKlasWEFJSUl6P1paWtLX1UMPPcSBAwdobm4mIyODRYsWsWzZMrZv387777/PvffeS1ZWFq+99hrPP/88586dY+XKlfh8PsxmM3PnzuWxxx5LL79+/XoWLlwIaGGkv7+fbdu20dTURCAQwGKxUF5ezqpVqygtLcVsNqf3v7u7m/r6etra2hgfH0ev1+PxeJg2bRoPPPAAZrMZSfr4kTGdnZ3s37+fAwcOEAgEyMzM5K677iIQCNDT00NRUREPP/wwANu3b2ffvn14vV6qq6vZvn07/f39TJs2jVWrVlFdXU0oFOL06dNs27aNrq4uUqkUXq+XGTNm8Ad/8AdkZ2cjSVL6Z6+trY1HH32U0tJSJEni5MmTvPvuu/T393P33XezcuVKJEnC7/fz9ttv09bWxoYNG6iqqsLv97Nr1y6OHj3KwMDApOvi3nvvpaKi4rYahweiBUoQBEEQhCuUSCRob2/nxIkTjIyMkEql0t3Mjh07xsjICPfffz9FRUUAhEIh9u3bx8aNGxkbG8PhcDAyMoLf7+fIkSO0tbVx33330d/fT1NTE6FQiGAwyL59+4hGozz00EPU1NQAWhGB3t5ennvuOQ4dOkQymcThcJBKpTh8+DDt7e08/PDDzJ07F4vFQiwWY9euXbS0tDBnzpyLAtTu3bvp7+8nNzeXhQsXEo1GOXjwIK+99hpdXV2UlJSQSCTQ6XS0trZy5swZdDody5YtQ6fTpVuBJv5tNBoxGo3p8HgpsizT29vLiy++yP79+4nFYjidTmRZ5vjx47S1tfHggw+yYMGC9Hp1Oh3ApG180g07QF9fH42NjbS2tpJMJpFlmVAoRHNzM729vdx3333MnTs3vfzbb79NfX09wWAQh8OBTqcjEokwMDDA3LlzKSsrY3R0lA8++IA33niDcDhMRkYGkiShKAqNjY2cOnUKg8HAnDlzcLlcRKNRmpubee655zh58iRmsxmTyUQ8Hufs2bO0trbyzW9+k+LiYsxmM0NDQ7z//vts27aNeDyOJEmkUin0ej2qqpJKpTh16hQbN26kqqoqHRQmzpHBYEifH71eTyKR4MSJE7z++uvMmjWLhQsXEo/H6ejo4Omnn6ahoQFJkrBYLCSTSVpaWmhpaeGb3/wmFRUVWK1WOjo6eOWVV9ixYweZmZkYjUZ0Oh1+v594PP6JIRa0ILtlyxa2bNlCMBgkOzubVCrF5s2baW9vx+/3s2jRonSAOnPmDG+99RaSJLF48WLi8TgGgwGdToeqqgSDQY4cOcIzzzzDuXPncLlcGI3G9M9kR0cHX/va1/B4POh0Os6cOcM777zD9OnTKS4uRpIkGhoa2LhxIx0dHciyzPLly5Ekia6uLrZu3Up3dzcbNmyYdF0EAgGcTmf6uujv72fevHmUlpaKACUIgiAIgvBJdDodZrOZOXPm4PP58Hq9yLJMa2srr7/+Ov/93//N1KlTyc7OTj/FB60AwJkzZ1i7di1r164lkUhQX1/Pb3/7WwYGBpgyZQq1tbXMmDGDQCDAL37xC958800qKyuZOnUqRqORWCxGfX09L7/8MhUVFWzYsIGamhpGR0d59dVX2bhxIxkZGeTk5FBRUfGZjzEajdLd3c2SJUtYsWIFFouFAwcO8Hd/93ds376dkpISamtrWb16NWfPnmVoaIivfOUr3HPPPQCfeEOdTCbZtm0br7zyCnl5eaxfv54ZM2YQDAZ59dVXefvtt7FareTn51NWVsaXv/xlCgoKOH36NMuWLeNP//RPKSgowGKxfGJQMxgMTJ06laqqKnJzczGZTAwPD/P6669TX1+PzWajpqYGi8WCqqq88MILhMNhVq9ezT333IPVaiUQCHDq1Cl8Pl86xMmyTDgcpr29nW9/+9ssXLiQWCzGu+++y89//nNefvllsrOzycjIoK+vjy1btvDb3/6W++67j9WrV1NUVERfXx/19fW88MILTJ06lS996Uvk5uam1z8+Ps7Zs2d54oknmDNnDna7/ZLHWlZWxqpVqzh37hy9vb18+9vfZtasWQDp4/qooaEh6uvrefLJJ1m1ahVr1qyhvLyc0dFR3n33XZ555hnKy8txuVwUFRXR0tLCSy+9RHl5OY8++iglJSXpbpWBQOBTg+yhQ4f4/e9/z9jYGI888ggLFiwgHA7z5ptv0t3dTTwev+g1iUSCYDBIIpHgK1/5CoWFhSiKQkZGBmfPnuWNN95g8+bNPProo6xYsYKMjAyOHTvGW2+9xa9+9Svq6upYsmQJHo+HgoICJEni2LFjrFmzBlVVOXfuHKFQCIvFwokTJ9Ih9ezZswwPD5OTk0NJSQmKovD8888TiURYs2YNd99996TrIjMzM31d3E5EgBIEQRAE4YrYbDbmz59PbW0t0WiURCKBoii43W5sNhvf/OY3aW5uZubMmembYtC6Qq1fv56HHnqIwsJCkskkVVVVvPrqqzQ2NvLII4/w+OOPYzKZiEQi+P1+fvzjH9PZ2Uk4HMblchEOh3nmmWfQ6/X8yZ/8CQ888AB6vZ5UKsXcuXPZsGEDe/bsYcaMGZ8rQMmyzLp161i/fn36GPLy8njuuedobW2lvb2dWbNm4XQ6sdvt6S5dOTk5n7heVVWJx+O88MILyLLMI488wmOPPYZer0eWZWbOnElbWxsHDhxg1qxZVFZW4nK58Hq9GI1GHA4HPp9v0vifj1NTU0N5eTmRSIR4PI6iKGRmZvLwww9z+vRpTp8+TW9vL+Xl5elWsZkzZ3LnnXdSW1uLyWTCaDSyZMmSi9atKApf+cpXWLp0KT6fD4DVq1dz4sQJNm3axLp166isrKSpqYm33nqLoqIifvjDH1JcXIzBYEBVVcrLyzl+/DivvfYad9xxR/o8q6qKyWTi29/+NkuWLMHtdqe3GwqFJu2HyWTC6XRis9nSBSMufA/8fv9F57+9vZ2XXnqJrKwsvv/97zN9+vT0PtXU1LBv3z62bNnC3LlzKSgoSLeI3n333cyePZvs7GyMRuOk1ruPe68Btm7dytDQEOvWrePP//zP09+faNHbsWPHJc9vXV0dX//615k+ffqkdZ46dYodO3ZQU1PDP/3TP+F2u9HpdMyaNYusrCz+4i/+gpdffpnq6mpcLhe5ublkZWXR0NCALMuoqkpbWxsej4fKykoOHz7M2NgYPp+P1tZWEokEZWVlWCwWUqkUPT09zJkz57Kui9uFCFCCIAiCIFyxeDzOa6+9xubNm2lqamJsbIxYLEYqlSIYDDIwMEAwGJwUoIxGIzU1NeTl5QFaC4nH48Hr9VJcXExhYWG6K5Ber0/fxAWDQYLBIE6nk3A4TGNjI6tXr053R5pYPjc3l5kzZ3Lo0CG6u7s/1/GZzWbKysouKjyQl5dHS0vLRTfyl0tVVaLRKE1NTSxcuJCysrL0MUiSRE5ODtOnT2f37t10dHR8rmOQZZmdO3fy5ptvsn//foaGhohEIiiKQigUwuv1Mjg4SHl5OQaDgbKyMvbt24csywwNDTF79uyPDaGSJDF79uxJ4cbhcHDnnXfy8ssv09fXRyAQYGBggO7ubh5++GHcbvekAghut5s777yTN998k2AwOGn9Ey2cGRkZn+scfJSiKAwPD3P27Fm+/OUv4/P5Ju2Tw+Fg2bJlvPHGG/j9fiRJwu1243K5+K//+i8ikQhLliyhpqbmskIskA4rE91QJxQWFlJeXs6JEycueo1OpyM3N5fq6upJX0+lUgwODhIMBtNjry7c97KyMqqrqzl27BjhcBiA/Px88vLy+OCDD4jFYgwMDDAwMEB1dTVz587l4MGDHD16lCVLltDa2oqqqun3feK62Lt3b/q6mDVr1ud6OHErEAFKEARBEIQrMjg4yDPPPMPLL7/MjBkz+PrXv47P50OSJEZGRvjRj35EIpEglUpNep3dbp802F6n0yFJEmazmYyMDMxmc7o7kE6nw2KxpMfATPwJhUIkk0k8Hg9Wq3XS8hMlrmVZJhqNfq5jtFgsF40z0ul0GI3G9L58Fhcew0SL3aWOYSJofR6vvPIKL774IkC6G6DJZCIcDvPkk0+SSqVIJpPp7f/1X/81b7zxBgcPHuSnP/0pkiSlC0jce++96TFtkiRht9sxmUyTwofBYMDr9aaLEYyOjhIOhxkYGODll19m165dk8bKxGIxent7GR4ennQ+DQYDGRkZ6bFGV1M8HicUCjE6Osobb7zBoUOHJoWQRCJBb28vQ0NDxONxdDodM2fO5B//8R/53e9+x6ZNm3jllVdwuVzMnDmTtWvXsmbNmo/d3vj4ONFoFLvdflEZdUmScDqdOByOi15ntVov2W0xFosRjUbR6/VkZWWlrxn4sGutx+Oho6MjfU5zc3OpqKjg7bff5uTJk3R0dGAwGCgpKaG0tJTS0lIOHTpETk4OfX19uN1uKisr0+v927/9WzZu3MihQ4f4yU9+giRJFBYWsmbNmknXxe1EBChBEARBEK7I2NgYr732GtnZ2axdu5Z58+bhcDhIJpOcPn0ak8l00diTiQH+kiRNuimeCFET3/vo1ycGzquqiiRJmEwmdDpdurXroyZuei+88ZzonqUoykXLf9x69Hr9Jce2fN4b+guPIR6PX3LbE5PjftL4psuxdetWYrEYq1at4v77709XRmxvb0+3HF34Ps2cOROHw8GSJUvo6emhvb2dpqYmnn32WfR6Pffee2/6NYlEgmQyiaIo6RA1MTZKURTMZnN6jJbVaqWmpoYFCxZcVE1x4j0pKyubdI4miiZc7QCl1+sxGAyYzWaqq6tZsGDBRcFm4nqrra0FtOqS99xzD3l5efT19dHV1UVLSwvNzc309PSQlZVFXV3dRccGWhdDg8GQDqsflUwmL/n1C4uTXMhgMGAwGFAU5ZIBW5Zl4vE4JpMpff1mZmamWzoPHz5Ma2srTqeTwsJCfD4flZWVHDx4kNzcXEZHR5k1axbl5eXpdU5cF3fddRc9PT20tbVx+vRpnn32WQwGA2vXriU/P/8yzv6tQwQoQRAEQRAu28QYnpaWFh5//HHq6uooLS0FYGRkhLa2ts/cOvNp9Ho9drud3NxcOjs7GRkZQVGUdBW4icIGVquVzMzM9Gs8Hs+ksVoTy8diMYaHhy85iP9K92tibMmnkSQJm81Gbm4u3d3dDA0NXXQMnZ2dmEym9NiiKzWxH+3t7fh8PmbMmMHUqVPT39+7dy/j4+MX3fBbrVbq6uqoq6sjGo3S29tLQ0MD3/ve9zh06BCzZ89OV8OLx+M0NzeTn5+fDmORSISjR4+mW0c8Hg9utzu9zIMPPjipGMWFLuwK+FlMtFR+2ntgMBjS++RwOPijP/ojiouLL7lPLpcr/Rqfz8ddd90FaA8QWlpaePnll3n11Vc5fPgwFRUVHxugsrKy6OjouKhb6UQXx4+O0/okJpMJl8uFyWTi1KlT6WOeCOTDw8N0dXVRWlqa3h+r1UpOTg65ubkcPHiQ1tZW5s2bR1FREW63m+rqat5++228Xi+pVIqCgoL0z8/E6z96XRw/fpy//Mu/TF8XIkAJgiAIgiB8AkmScDgc6bFJsViMZDJJc3Mz9fX1n7vr2Sdt1263s3TpUnbt2sWBAwcoKCjA6/USjUY5duwYp0+fnjRGY2JOpk2bNtHW1sbAwABut5vx8XEaGhro7u7+XONs9Ho9LpeLVCpFf38/AwMD6ZYXu91+yWOwWq0sWbKE9957j/3791NWVkZmZibxeJzjx4/T1NTElClTLhr/cqXsdjvxeBy/308kEkGv1zM8PMz27dvp7e1Nj+FRFCUdiCwWS7r7nN1up6KiArPZnJ7IdqK1SZIk3nnnnXR3L1mWaWhoYNu2bZSVlVFYWIjdbqekpITZs2dz/Phxzp49m+6uKUkS8Xg8PU7H4XBM6kp3JYxGIxkZGSSTSfr6+hgaGkoXOvgovV5PXl4eixYtYvfu3bS0tJCRkYHH40GSJBKJRHp8m81mS5+zifM10W00OzubvLw8dDodyWTyksFtogVtojDIwYMHWbx4MdnZ2SSTSY4cOcLp06fTLY6XQ6/XU1JSQnl5Ofv27ePAgQPpCpU9PT3s2bOH4eFhHnnkkfR1rdPp0kHp0KFD9Pb2smbNGgoLC9NfHxgYYN++fRQWFlJYWJhu5fqk68JisSDLMrIsf6b37WYmApQgCIIgCJdNp9ORkZHBsmXLOHLkCPv27cNgMBAMBtm2bRvHjx8nkUhcs+3bbDa++tWv0tTUxKuvvkpPTw8zZ85kZGSEF198kVQqxfLlyyeVsr777rt56qmn2LFjB263m+nTp9PV1cXTTz9NKBT6XK0fZrOZyspKbDYbO3bsQFGU9BP8+fPnX/I1JpOJxx57jMbGRt58800GBgaYN28egUCAF198kVAoxLJlyz61ytvHmWhNmT9/Plu3bmXXrl0UFxdjsVjYvXs3+/fvZ2xsLL38RHGAn/3sZ+nJkD0eD+FwmF27dpFMJqmpqaGgoIDBwcH0uLWdO3ei1+upra0lHA6zc+dOWlpa+OEPf5iesHXatGls2LCBffv28ZOf/ITly5dTWVmJ0WhkdHSUjo4ObDYbTzzxxGcuTGC325kyZQoWi4UtW7bg9/vJyckhLy+PkpKSi5YvKyvj8ccfZ8+ePfz7v/87d911F7W1tZjNZvx+P+fOncNms/HHf/zHFBUVsWvXLp5++mnuuusu8vPzMZlMtLS08MEHH5CTk8Mdd9xxydanCatWreLUqVPs3r07fX2Gw2F+//vfpycJvnAs2aepq6tjzZo1/PSnP+V//a//xZo1a3C73Rw6dIjdu3dTUVHBQw89NKkVye12U1NTw0svvYROp6OoqIjc3Nx0sRSPx0NrayuzZs2isLAQ+PC6+Nd//Veys7Oprq7G7XYTCoXYtWsXqVSK2tpaCgoKruDdujWIACUIgiAIwhXJzc3lhz/8IT//+c958skn+bd/+ze8Xi933HEHP/vZz/izP/uza7Zts9nMHXfcwT//8z/z0ksv8d577/Hyyy+nuxl961vfYvHixemn70ajkZKSEv7u7/6O5557jh//+MekUimmTp3K448/DvC5Al9GRgbLly/ngQce4N1332Xz5s1IksTSpUt59dVXL/kag8HAvHnz+NGPfsQrr7zCe++9x2uvvYbZbKa2tpa/+Zu/YenSpekuZJ/VN77xDYxGI2+99Ravv/46JpOJ2tpavvWtb/HrX/86vdxEKC4uLmbPnj1s2rSJcDiMzWajqKiIH/zgB6xdu5a8vLx0gHI6nfzDP/wD27dv5z/+4z8IBAIUFRXx/e9/n0cffTTd/dDlcrFixQqeeeYZfv3rX7N582aeeuqpdDe/adOm8eUvf/lzHavX62XlypVs2LCBnTt38sorr2AymVi3bh0///nPL1re6XSycOFCnn/+eX7zm9+wY8cOXnjhBYD0mKANGzaQmZmJ2WzG5/PhcDh4/vnnGR4eRlVVfD4f8+fP53vf+x5z5sz5xABUVVXFN77xDZxOJ5s2beKNN96goKCAhx9+mOzs7HRgu1x5eXk88MADuFwunnrqKX7xi1+QSCTIzc1l5cqVfO1rX7toctuJohc6nY4pU6aQk5OTbvGz2WzMmzePHTt2MGXKlHQguvC62Lt3L2+99Vb6uiguLuYHP/gB9957b7qq5u1Ep15Oh11BEARBEITzFEUhmUzS3d2N3+8nmUxiNBpxuVz4fD6am5vJzs4mOzsbm82WrrY2OjrK1KlTJ90sp1IpTp06hdVqJTc3Nx18FEUhEolw9uxZ3G43OTk5WK3W9OvGx8cZHBzE7/eTSCTQ6/U4HA7y8vJwOp0XFWDw+/3p0uqKoqTHIU2Mo8rKyiIrK4tEIkFPTw9jY2OUlpbi9XrT65iYQygcDqePb6LgQFdXF6Ojo+nuWC6X66Ky1R8VCoUYGhpibGyMeDye7ho5cQwTN8ATZcdbW1vJzMycdPP7SZLJJIODgwwPDxOLxdDpdNjtdnJychgYGECSJPLz88nIyJg0MWw8HkeWZSRJwmKxkJOTg8fjwWQycfToUX7xi1/wzjvv8M4772C1WvH7/aRSKaxWK1lZWWRnZ086/7IsE4vF6OvrS08OC1pLnN1ux+fzpbuHBYNB+vv7CYfD1NXVXdQNT5bldFfJgoICcnJyUFWVVCpFV1cXfr8/XUjE6/VSXl6eXr64uHhSt8VYLEZ/f3/6mEEL3DabDZ/Ph8vlwmAwMD4+nt6nC/c9IyODrKysywp/4XCYoaEhhoeHSSaTmM1mzGYz//mf/0ljYyNPPPEETzzxBAD9/f0MDQ3hdDrT4wsv9d4GAoH0fk3MneXxeMjNzcVisUwa1zUxOXFTUxMWi4XS0lI8Hg+gPUA4d+4cfr+f/Px8srOz05MQf9x1YbVayc7OTl8XtxsRoARBEARBEITLMhGg6uvr2blz56RqbcKlJRIJGhoaGBwcpLCwEKvVytjYWHqOrqKiIv7+7/+eurq6G72rwmW6rl344vF4evIuk8lEbm5uemZtQRAEQRAEQbjVKIpCU1MT77//Pna7HZ1Ol662mJeXx6pVq5gyZcqN3k3hCly3ABUMBmltbWX//v0MDw9jMpkoKChg6tSpTJkyZdJAN0EQBEEQBOGLx+l0Mm3aNMLh8KQulcLH0+v1ZGZmYrPZ6OrqIhKJYDabqaurY8WKFSxYsECcy5vMdenCp6oqBw4c4MUXX6SpqYlVq1YxNjbGoUOHcLlcPPTQQ6xevXrSjOKCIAiCIAiCIAhfNNelBSoajXL06FHa2tp48skn05VZhoeH2bhxIy+++CLJZJL169fflgPRBEEQBEEQBEG4OVyXANXV1UUoFKKqqor8/HwMBgM6nQ6TycR9992H0WjkqaeeYvbs2ZSUlHzmidRAq+YzPDyMLMt4PJ4rKgspCIIgCIIgCILwSaTrsZHh4WFSqRRFRUUYjcZ0Nz2j0UhxcTFlZWWcPn2a+vp6/H7/pNdOlFC83J6GwWCQF198kY0bN9LT03PVj0UQBEEQBEEQhNvXdWmBMpvNZGRkXHKAXCwWIxKJoNfr2bJlCzU1NYyMjDA2NkZfXx+hUIhp06ZRW1uLw+H41G1Fo1F2795NIpFgxowZTJ069VockiAIgiAIgiAIt6HrEqAKCwsJhULpScou1N3dTVtbG9OnTycWi7F//35sNhvDw8P09vamw1VFRcVlBShFUQiHw7S3t+P3+1EUBUm6Lg1tgiAIgiDcYlQVZFklkVBIJBRkGRIJhWRSRZZVZBkURUVRtOUURUVVtddNmKiPpdOBXq9Dp9Oh12v/1ut1GI06TCYdTy4vOgAAIABJREFUBoP2b4tFSi8nCMIXz3UJULm5ueTm5l70dVVVaW1tpbW1la9+9au43W7q6+sZGRmhpqaGRx55hOrqaiRJuuwPEVmW061XIyMjxGIxMQ5KEARBEIRLUtULw48Whib/GyIRmcHBBKOjSaJRleHhJIFAikhEJhJRiMVk4nGVSEQhldJen0p9mKAkCSRJC0gmk4TJpIUku13CatXjchnw+Qw4nXo8HiMFBSYcDj16vYQkgcGgS4ctSUIEK0G4wa7rRLoflUwm6e7uZmRkhOXLl2MymZg3bx6qqmIwGDAajVfceqQoCiMjI0ydOpWRkRF6enpENz5BEARBEC5JUaCnJ0Z3d4KBgQSDg0na26OMj8sMDiYJBrVx2DabhMtlxG6XyMoykpFhwOczYrfrsVolTCYJi0XCaJxoSfrw/mWiZSqVUonHFRIJ7e9QSCEalQkGU7S1RRkbSzE+rv3fbJbw+YwUFZmpqrJRWGimrMyCz2fCYhEBShBupBsaoJqamvD7/UybNi09M/PnqcCnqiqpVAq/38/q1avp7u6mqamJKVOmiG58giAIgnAbk2WV7u44nZ0xBga0sNTaGiMcljEYdNhseux2PQ6HnpISCyaThMdjwOvVQpLRqHWv0+s/7G430So00TIkSRMtRBe3Eqmq1rVvomVLUSCV0oJVMql1EUyltJA1Pi4TCHwYps6di7JrV4BYTMHlMlBWZmHqVCtFRRbKyy2YzRKSJEKVIFwvNzRAnTp1ikgkwrx5865KwEmlUkSjUcxmMwsXLmTz5s2cOHGCu+66C4/HcxX2WBBuPaFQisHBJIODSSIRmfnzndjtevHLWBCEm1YyqRAIpOjtTdDbG2dgIMnwcJJkUutWZzCA2SxRVmbB6dS60Dkcemw2PTabhN2ux2SScDgkHA4DZrPE9ew1l0wqRKMK4bBMOCwzMpJiZCSZ/n8oJHP0aJj33w/gcOgpL7dQXW2jtNSC2228rvsqCLejGxagFEXh3LlzpFIpZsyYcVXWGY/HCQaD+Hw+qqureeONN+js7GRoaEgEKEE4T5a1p5sjI0m6u+N0dcXo7dW6rYBKRYUFq1U8zRQE4fqLxWSA84Hl8j+DZFnrEjc2lqKnJ05vb5zh4SShkJwew6SqKpmZJnw+Ix6P1v3O5zPi9RqxWnXo9V+cnipGo4TRKJGRod2mVVRoX1cUlbGxFN3dcc6di9HWFmV0NEVHR4yhoQSnThkpKDBTUmKhsNCMwaATn+WCcA3csAAVDAYZHR3F5XJRVFR0VdYZi8UYGRkhLy8vPYluIBCgr6+PysrKq7INQbgZRSIfPrUcHZ345RulsTHC2FgSo1HC4dCTlWW8qHqUIAjC9dLRESMSUSgqMuPzmT5xWVWFWExraRoeTpxvSU/Q1hajry+BqqoUFJiprrZTUGCipMSM223EZPriBKUrJUk6MjONZGYamTnTQSqlMjSkHfPBg+McOjTOsWMhKiqs1NXZyc01kZNjxm4XD8UE4Wq6YQHqzJkzmEwmCgoKMBiuzm5Eo1EGBwfTE/ZaLBZ6eno4d+4cy5YtuyrbEISbgTYBtdYNJJVSOXMmQlNThFOnwpw4EcbvT2EySVRX21izJpM5cxxUVFhxOm9or15BEG5jqZTC1q1+zpyJsGqVl/vuy7xomYlxRBOFGDo7teCwb1+Qrq4Y5eVWlizJ4OGHsyksNN/UYelyGAw68vLM5OWZWbjQRU9PjD17AtTXj/Hqq0PMn+/k3nt9TJ9uw243YDCIECUIV8MNu1tqb2/HZrNdsrz5ZxWJRBgaGqKkpASTyYTVamVkZITW1tartg1BuBlEIgqdnTH27Aly+PA4HR0xxsdlLBaJwkIzy5a5WL7cS1GRGYdDnx4YLQiCcKOcOhWhpSVCR0eU9vboJZeRZZWRkSSbNo3y/vt+IhGZ6mobGzZkMWOGHatVwmzWur/p9df5AL4A8vLMrFvnY9kyD0eOBHnnnTH+/d+7mTvXzvr1WUybZr/RuygIt4Qb2oXPYDBgt0/+Yd67dy8Oh4Pi4mJcLtcVrTMUCtHX18fixYsxmUyYTCZCoRD9/f3E4/HPVeFPEL7ozpyJ0N4e4/TpMK2tUcbGZMbGUrjdBmbMsFNVZWPKFK0ErsOhJzPTiMUiunUIgnBjqapKIqGydesokqSjuNjC2Fhq0jKJhEJra5TduwMcPjyO02lg3jwHNTV2ysqs+HxGMjL0l6x+d7uYmKTXatUKYCxc6GLKFBtHj2rd+n796z7uusvN2rWZGAw6UWhCED6HGxag8vLyaGxsZPfu3UiSRCgU4tSpU3R3d7N69WpKSkqueJ2hUCg975PJZEKv12Oz2VBVlc7OTjEflHDLUFWtel5vb5yzZ2OcPRuhuzvByIhWSc9ikSgtNbNihYecHCM5OSZyc014vQbM5tvwsawgCF9IE93xtmwZpbs7zqxZDsrLrUiSVjAhFJLZvz/ImTNRwuEUFovEokUuCgvNFBSYyc83Y7frRRj4CL1eh9ttxO024nIZyMsz0dAQZteuAGNjKdas8eLzGUXPA0H4jG5YgKqtreXs2bN0dnaye/dukskkg4OD5Ofnk5OTg8ViuaL1ybJMKBRidHQ03YUPwOfzYbfbaWxsFAFKuGlpY5pU/H6t5PjAQIKenjgdHTFaW7U5TbxeIzk5RmbMsFNSYmHKFCuVlTZMJlGFSRCELx5VVQkEUhw5EuK99/xUV9tYuNBFebmVQCDFwYPjNDdHaG6OkEpBcbGZ2bMdTJ/uEJVCr0BOjvbwLD/fzDvvjPHBB37MZh1Ll7rJyzOJ8ygIn8ENC1BlZWWsX7+eEydO0NnZidPp5Etf+hJVVVXYbLYrXl80GmV8fByDwYDX60V/vvNzTk4ODoeDxsZG7r///qt9GIJwzUw8mQ2FZILBJKOjKdraYjQ2RmhrixIIpDAYJNxuAwsXZjBjhoO6Ohv5+WYsFtHKdK1FozKSpE2oebt2GRKEz0pVVYLBFMePh3jttSHcbgN/+IceSkosjI0laWgIs3XrGP39caZPt3PnnRkUF1uQJB3Dw0mcTj0ZGXoMhlu7SMTVYjRKlJdbefhhA/G4zI4dAWw2PUuWuMjMNN7o3ROEm84NLblVUlLymbrqXcrQ0BB+v5+KickSzsvKysLpdNLU1IR6vjazuNkRvoi08uHaLPSyrP3d0RHn+PFxDh0KceJEiGhUwWjUUV1t4447PMyc6WTWLAc225XNmSJ8dqqqkkyqNDdHsFj05OdrY8rE+ReEy6OqKrGYwpEjIV57bRhFUfkf/yMfn8+I359i27YxNm8exW6X+Iu/KKCw0EJfX5y9ewN0dycIh2Vmz3awZEkGHs8nlzoXPiRJOnw+E//zfxbzv/93J3v2BLBYdKxY4RVd+QThCt0yNYsHBgYYGxu7aL4nr9eLw+Ggra0NRVGQJPG0Svji8vtTHDkyTlNThEOHxhkYSBKLKVgsOqZNszFzppOFC53k5JiwWLTqeUaj+MV3PckybNkyysaNQwwPJ1m+3MM3v5mH3X7LfJwKwjUViym89dYI77/vJy/PxLe+lY/Xa6CxMcLvfjdIX1+COXMc+HxGtm4d49ixMAYDFBaaycszkZ9vpq0txrx5zht9KDetRx/N5pe/7OH48RA1NTaKiqw3epcE4aZyy/zG9/v9JJNJFixYMOlJsF6vx+Vy4fV6aWpqoqKi4orHVwnCtaCqKooCra1R2ttjNDVpczWNjmqFIFwuA3fc4aSmxk55uQWXy4DLZcDjMVyVbmPNzRFGRpLk55soKRG/PC+Xqqo0N4cJBmXcbgNer5FU6tNfJwi3O1VViUQUXnllkIaGMFVVNtau9ZKRYeD99/28884oPT1x4nGFPXsCFBWZqaiw8thj2eTkGHG5jFitEgaDjmRSxeMRXc+u1MSvjexsEzNnOmlpiXDoUEgEKEG4QrdMgKqsrMTtdlNeXj7pxlKn0+FyuSguLubYsWMUFhaKACXcMKmUwuhoiq6uOH19WgW93t44Y2MpolEFs1lHba2d4uIPn7Tm55vxeg1XfaDv3r1BOjpiLFniEgHqCqgq+P0yZrOOBQsyWLQoA4tFtGwLwidRFJVIROb114c5diyE12sgJ8fE6dMRNm8epbExxPBwirIyC1OmWHC7jXi9BoqKLBQUaN1kxXinq8dolJg920FXV5xTp8KsXu3FYhFdwQXhct0yAaq8vJzy8vJLfs/tdlNWVsaRI0dYuXLldd4z4XaWSqmEwzJDQwnGxrQKel1dMTo7YwwNJc/P02QkO9tIQYGZsjILZWUWSkos13yOpubmCB0dcWprb76JFVMphYEBraUuO9uEy3V9P8pkGUwmbVD21KlXXvRGEG43iqIyPq6NbwqHFZxOPSMjSc6cSXLyZJhkUuHOOzOYPdtJdbWN/HwTRqMITNdSUZEZn8/IyZMJurvjVFSIB2mCcLlumQD1STweD+Xl5bz55ptEo1FUVRVPWYSr7nyNEuJxmXBYq543Npaiu1vrntfdnaCvL04spt08ZGUZmTNH66JXWWklK8t4XZ+wyrKKqnLTzZ8y0Q3o3XfHGB9Pcc89blwuxw3Yjw/fc0EQLoc2Se7QUJJkUkVRVCoqtElwDQa47z4fBQViwvvrxWLRU1Bgoq0tyrFjIcrLLUiSKLQlCJfjtglQFRUVtLa2kkgkbvTuCLcQVdVCiFY1T2txam+PcuJEmKNHQ+kxTXq9jqwsIzU1dmbPdjBzpp3ycis63Y37ZaXX6zAYbr45ohRFZXQ0xbPP9lNUZL4hA8n1em0/FEUkKEG4HAaDRF6emX/+57IbvSvCBQoLzfh8BvbtC7JqlRe7XRIV+QThMtwWAUqn01FQUMBPfvITsrOzb/TuCLcQRYHBwQSNjRGOHw/R0BBiaChJJKLgcOipqLBQVeVl5kwHRUVmnE6tAITRqLvhLT+plIpOBzdbYcpgUKaxMUw0qjB1qg2v9/oPJDebdciydg4FQRBuViUlFurqHBw9Gubpp/t59NFsfD5RGl4QPs1tE6CcTidr1qzB4XCI5mnhM1MUlXhc4ezZKKdPR2hpidDVlWBsLEkoJJOba+KOOzKYOtVKaamZzEwTTqcel8uAxfLFerKXSqlI0s0ZoE6eDCPLKtOn28nK+vQANTG/ll6vtbhNvI+RiExm5pXdLOh0WtcXWdbm6xIEQbhZmc0SM2c68HqN2GwSTqeYhF0QLsdtEaAADAaDaH0SPpNkUmFoKElXV5yOjhhdXXF6e+MMDGjdQT0eA9OnOyguNlNQYCIry0Rurgm32/CFHgStBSjdFyrUfRqt+5426Dw310RpqQWH48Nf+KqqhZr+/gQOhx6HQ8/4uEJjY4gDB8ZZtcpLcbGZM2ci7N8fJBZTWbnSw9SpViyWy79xMJslUikl3QKVTCqMjibp7k5QXGzG4zGIimGCIHzhSZIOt9uI233b3A4KwlUhfmIE4SMURSUaVRgeTjA4mGRgIEFnZ5y2Nq3kuCyruFxGSkos50vuWikutlBcbMZg+PzzM10viYSCXs8XNkBpRRq0ubK0ljIdgUCKc+di9PYmmDfPgcfzYUhNJhWGh5McOjROe3uMggITs2c7kWXYsSPAli0jzJxpJ5FQ2LbNT339KAaDDqtVoqDAfFGAmth2R0csPYbNZtOj0+mw2SQURTuHo6NJWlujHD48TkdHnDlzHNx5ZwZFRZeeLmHiuFQVMWBbEIQbTvsIEp9DgnAlRIASbnsTrRbhsEI4LBMIpOjvT9DYGObkyQgDAwlkWcVmk8jJMTFnjpOqKhtVVVYyMq7+/EzX2kTluFhMwWrVYzRe/f1XVZVYTCEQSGG16nE69emuc9GogtH4yQUs4nEFvz/F8HCSaFTB4zGQnW2krS3GoUPjyLJKTY0Nq/XD8NTfn2DnzgBPPdVHOCxTUmLBYJAoK7PQ35/AaJRwOAwcODBOQ0MISQKDQUdjY4R4XLnoHKkqdHXF2Lx5BIdDz113uaio0EqWTxzP0FCSAweCvPeenwMHxlEUld7eOJmZxo8NUOGwVs4+FJKpqrJiMom5VwRBEAThZiIClHBbmmhdmBjHMjqa5MSJCIcPj3PiRJiurhigddVasMDJHXdkMH26VjnvZgtMH6WeT1CRiHK+qIU06evJpHZOJEkLORe2UF143pTzmUOn4/zYItLnRpZV2ttjvPPOKLW1dhYtysBu15NIKDQ0hCgoMJGdbbpEq8+Hr926dZQ33xwhGEwxd66Thx/Oor09zp49AcxmiYoKGxaLHlXVqvLt3OnnySf7cTh0gOF8C5E27slolDAYdKRSKo2NEXQ6mDPHSW9vgmhUuagcuapqY6SefnqA3bv9FBVZyMkxUVFhQ6fjfPdMHXv3Bjl8eJyhoRTz5jnw+2VCIZlIRL7kuU+lVE6cCPHcc4M0N0d45plp5OSYbnhBEeEmMHGRplJa9Rq9HgziV7ggCMKNID59hdtSIJCitTXK8eNhGhpCtLfHCIUUFEUlJ8fEhg0+amsdVFbacLn0mM0SJtONr5x3tUSj2vgds1mHyfThQSWTKs8+28/eveMUF5tZs8bL/PkZ6e8rCjQ2htm7N0hraxRFUfF6Tcydq5Vmz8kxp5c7dy7GwYNBhoaSeDwGamvtnDkT5uc/72LRIhfr1mVSVXXxJLTvvTfGW28N09oaJTvbSGWllbNnozz9dD/xuHo++EmUl5vPV8NT2bcvyOuvD+Ny6fnzP8/nV7/qJTfXRHa2EZ1Ou89MJFT27AnS1xenrs5OVZWNzs5h7JeYR9jvT7Fp0wj79wcJBGSmTpWw2T4c05SVZcRs1tHeHiM318SqVV4eeyyb//N/uojF5I+9TvbsCbBxo3Zss2c7sdnEgG3hCigK/O53cO4czJ0La9bc6D0SBEG4LYkAJdzyFEXrTtbZGaelJUJLS5SurhgjIylCIRmjUUdFhZUpU6yUlFjIyzORmWkkI8OQ7qp1qwQn0Fp4gkEZWQabTY/FIp0vvBDnt7/t59ChEKGQzMhIgqwsI/PnZ6CqKqGQzMaNw+kQoqoqHo+R5uYYx4+Ps2yZmxUrPEydasNg0DFvnpN33hllYCBBb2+CoiIze/YEGRlJUlFhJTv74up5u3cHqK/XXrNokYs1a7wMDSX5v/+3l5YWrVVQr4eMDCMOhwG9XmsF2rnTj8WiY/16H729CWIxhaoqK2VlFiIR5Xzrk8LBg0F0Oigvt+L1GohGZQoLzegvyDHDw0n27g2wceMQVquE2SxhNH4YNHU6KCuzMHOmE5/PRF2dnXvu8eDxGAiFZMxm6ZIFKT74wM+mTcMcPx5ClrUWrvHxFDabdNO3agrXmKrC+Dj85jeweTP09moD6FauvHatUKmUtl3jNZomIJGAHTtgyxZYuhRWrwar9dps60KyDO+/D3v3QkUFfPnLTPoAEARBuAwiQAm3pERCYWAgQXd3PP2nvz/BwECCREIbz1RaaqG01EJmppG8PK1yXmbmRKGAG30E144sq4yNJVEUFbtda13r6orx9tujbN/uZ/ZsJzodnDsXpa8vQTKpACpvvz3Ku++OotdLLF7soqTEgsMhMTqaYscOP/v3B3G7DZSXW9HrdeTkmCgqMtPQEGJwMEEgkOLw4RBZWUZKSsxkZBgu2Cft/dq6dZSenjgzZzq4/34flZU2TpwIYTBIJJMKZrOE223A7daq3AWDMvv3B+nvTzBtmp3KShu//GUvGRkGKiutZGUZ6eqKp7vvdXfHmTfPSUGBiXhcC9Y+nzHdTXFsLMnhw0HefnsEWVZZvTqT7dvH0mOiQAtQLpeRVau8RCJa6frCQjOhUIrR0SR5eeZ0a5WqauOz9u0LsmnTMG1tMWw2LbB2dsbZvTvA8uWej513JZFQ6O6Oc+5clERCZcUKD0ajdEtfnze9jg44cwaiUSgrg9raiWoh2vdjMQgEYGTk8tanqjA6qt3wb94MZjOEw1BfD14vzJ4NDgdX7aJQVTh2DNrawOWCmTPB57s6675QZ6d2PFu3wtmzWqvavHnaMV2rQKOqcPw4vPeedg6nTbt65024fKoKjY1w6JAW1DdsgIyMm29OjQmqqrUOJ5PaA4frFci1/vTads1m8SDgOhMBSrglJJMKoZDM8HCS4eEkg4NJOjpidHTEGBhIEI+rOBx68vK0UuPFxRYqKqyUl1uxWG7SD+3PSJZVhoeTyLKK06knElE4dizCe++NkZtr5ktfyqS3N8HwcJJkUmt56u2Ns3nzCDqdjmXLXNxzj+d8kQSVZFJrTamvH6OlJUoyqaA//0Gem2uioYELqhnGWLAgA7fbkA4tiqJ1y9u2zc/Jk2EqK6384R96qauzEw7LnD4dIRqVmTLFis2mhSaHQwsRzc0RzpyJ4HYbmDbNxtmzUc6cifBHf+Q7/95qVfMMBh2KAvG4SkmJ5XzLWQRZhrw8EwaDjlBI5ujREO++O0ZfX4K1azNZtcrDqVPh83NGaYO+dDodej3U1X3Y9y+ZVAgGZcJhGbfbgN2uzRMVCKQ4fjzMxo1D9PXFqa62UVpqoa8vwa5dAQ4eHGf+/IxJ96cTc1Z1dcU5ezbKiRNhOju1roJ33+2+Zg0CwlUyMgInT0JrK3g8cOedsGQJOJ3aDU40qoWHM2c+fV2qCmNjcOqUFqC8XqipAZNJCzjPPKN9b+ZM7WtX4wa0t1cLNV1d2vYOH9a2mZV19VqjolHYt087Bz6fdowvvQQnTkBVFWRnazeEV8vE04+ODvjgAwiFYNEirQVKBKjrZ+J9OHkSNm3SWh8NBrjjDqiuvvoBSvvQ18Ky13vtAlogoIXyWAzmz4eSEu3n8VpSVe2z5sAB7e/Vq7WfG+G6EQFKuCkpinbjHg5rN62joyk6O2M0NoY5fTrC4GASnQ7sdj0FBWamTbNRUWFl9mwnGRn627rLVCqlMjiYIJVSsVgkWlsjfPBBAICHH85i1iwHfn8ARVHR6WB8PMXvfz/CwECCBx/MYsUKD4WFExXmtK5tubkm7HY9qZSanhsJwOczYjTq6O2N09wcIRZTqauzT5q7KZFQaG+P8frrwzgcelas8DB7toNYTOHcuSjvvecnEpH50pd8GAxaSXJJ0qGqcPDgOKOjSebMcWK1SmzcOITXa+Duu90UFGg3YBNFLkD7/VlUZMZqlRgdTWI06igoMCPLcOZMmPr6UZqboyxc6OLxx3OwWiUyMgy0t0fp6oozOprE6734JjKVUhkaSpJKkQ6HPT1xGhrCvPjiAIFAijvvzOD++33U1Tloagpz6lSEYDBFMqmdL1nWWsRGR7UHADt3+jl4cJxgMEVZmZXaWvv5MvnX4qoQrpqsLKirg0hECx/79mk3cgsWQGbmRKUULqpccilDQ9pT+pMnobAQ1q7VWpuqqrQwcPw4bNumLVtTA3b7Zw8EqZQWZN55R+teN3euFvhOntRahxYs0FrU7PbPfiM6cewnTkBTk3ZTu2KFdrO5b58WBru7tWOpqNAC6NWQSGjrra/XQuCdd8Lixdq5FC4tmQS/HwYGtPcnO1s7XxNdRidaXEZHSVcU+jSKAsGg1hX18GHo69PWvX279j2P5+q2ooTD0NOjPQyYNUtr5TIYrm5oTqXg9Gn427/V1v2Vr8Af/AHk5Fy7EKWq2kOII0fgl7/U3odZs0SAus5EgBJuGhMV4BRFa/Ho6Ulw6JBWBe3MmSgjIyn0enA4JBYscFFba2P2bCcVFTd/5byrKZVSGRhIIssQCMg0N0c4dy7KPfe4ue8+rSkkHE6RSoHJJBGNquzY4Scnx8TcuRkXhKcP5zPq708QjcrYbNKkwghutwGrVU93dxxFUTEYdNTUfBigVFVrDduyZZShoQQPPlhAXZ0DnU7HuXMR/t//6+fUqTB5eSYqK60kEioGQ5BwWEZVVc6ejWKxSCQSKgcPhujri/Pgg1mUl1uxWrVtSNKHAcrpNJCVZUJVVcbGUhgMkJ1tpL09xrPP9tPcHGHpUjd/9md5OJ3ax+P/Z++8w+uqrrT/nnNu701XV11WtSRLlrvlisHGgA0G02JIgDAJKTPwkDaTycxkyMzH8DGpk5kBvoSQkEBCwIBtwGBjG9xwQ+6WiyzJ6uWq6/Z7yvfH8lWxJVcJFe/f8/ixJV+ds885+16td6+13p2ZqcOZM5ShMxoFPPjgxb+kJAno7pagKIBOx+PcuSAOHfJjy5YOcJyChx6Kx8qVTiQk9Ik6lYpihpiNfleXiJMn/Xj//XZ89lkXRBHIyzNg1SonFi+2w+MZ4RVNxvCQkkJ/li6l0rTnngO++13gmWfI9MHhoAB+7txLHycaBV5/nQLOmTOBX/6Sslj9xcvRo8Dzz1Mg9dhjQFHRtQWIskyB8Nq1QGsr8J3vAPfcQ+faswd46ikKEpcvB0pKAIPh6s8RK3NqaQHef59E4COPAEuW0P9/+9vAunUUEJ48SVm7VatI8HDctQW9sdrbhgbgRz+iY333u/QcRjpDMN7p7ATWrwf++7+B1FTgq18l0RkXR/NCFEkAvf02zdHLoSiUDfrkE/q5/HzKOu3bR+Jj+nQqR7Xbh0fgyDJlOPftozk9aRItArjdfXPqeumfIW5tBbKzgV//GvjLXygrnJIyMj2K0Si9Hw8dIlH77W+TYGN8oTABxRg3eL0RnDoVxKFDPhw/7us1CzAaBeTk6FFYaMLkyWQEodcL0Gi483vsjPbIxxb0ey8CAPjkkw5IEmWF1qzpEwahkNx731paIujsFLFsmQNO58CPjJh4OnbMB42GQ0aGfsD9tljIpKKlJQKfT0JcHPWbabV9PUJeL2VbsrMNKCoyweFQ48iRHrz5phcHD/ZAkoCcHAOcTjV8PgkmEwmynh4JwaCEzk4R+/d3Q5aBwkIT7r03DjZb3zh5vi9WyszUwmIREA7TflSBAPUnbdnSgc5OEcuXOy/6+VtusZ8X7GFuG0n7AAAgAElEQVTY7YN/ZKpU5MzH88Bbb3mhUnEAFGRkaPHIIx4UFRlhsfRlrhSFXAHNZg6BgIxt2zqwZUsHjh3zIxJRMG2aGcuW2ZGfb0BcnHpQUwrGGIfjgPR04Cc/AX7xC1p1DwSABx+k3qLL8ec/A++8A+TkAH/3dySeLvwwy8mh4PPppylw+8Y3SOBcLc3NwMaNJPZ+/GMyp4idr6SEAsKf/Qz46U+B+++nP1dyDf2JGWH84z/S1ytXUkDbn2XLgKQkEnI/+xmwYwddW0rKtZX0KQpl0P73fynY/I//IGHG6mAvj90O3HIL3feTJ2ker1wJfOlLQGEhZYqcThI+4fDlj9fcDLz5Jgn1Rx8lgaFWk1A/fpz+b9IkyqQkJV3/+A8epNK2pCRaXNi8mRYDbr+dxmw2X/85enpojp47B3zzm3RfamooK3zoEN27VavoXg1nj+LHH1NGNSuLhG1+PsumjgJMQDHGJJShpt6b06eDOHUqgNraELzeaK9omjnTjKIiE+Lj1XA41LDbVbBYVDAY2MaklyIalVFTE0IoROWPJSUW3HmnE25334psMCifL30D/H7pfHWFasCmuyQCZLzySiMqKkJYuNCK6dNNA+69w6GG0SggGqU9ogoKaPPbWEawvT2Ks2eD8Plk3HOPFXa7gJ07O/Hhh204eNCHUIjKnPLzjXC51LDZVMjPN+DIER9efLEBjY1RdHZKiERkOJ1qJCdrUFrag1BIRnGxGSkpWggC15uNSkvTw2wmkxCzmVzzPvigDYLA4d5747BkiQ2JiZoBe18lJGiwcqUTgYAMh2Pwj0y1mkdSkhZr1rhx5kwQPM8hK0uH4mITMjL0MJkGlo1KEs3vlhYFL73UAJ9PAs8D8+ZZMHeuBYmJWiQkaGA2C1CpbqwevQkDx5FyT0qi4OrVVynw8fuBr3xlaGOGUIgCsHXrKKO0ejUJiMHK5rRaIDMT+Id/AF56iYSOKAILF155wFZfTxmhN98EnngCuPlmWs2OlVKZTBSgff/79Jpt26iH6LHHAJvtys5Bu1ID/+//0fkef5zGeKHrntFIphsGA63mb9lC2a+bb6bsV3Y2oBt8g+qLkCQKmN94g0oQ/+mfKOtnsbC+pytBEIDERODWW6lHKSODSiBfew144AESIQYDCZ7LlfCdOkWlodXVwN//PT17l4uegyj29aOtW0fzZNas6xNRsRLRhAQyqJg6lcT52rUk1lQq+n5m5rWfQxSBd98lIbNyJc1pi4VK6+bMIafHnTtp24FvfpP6ooajr+/tt4Hycrqmhx6icmG9/srfF4xhgwkoxpggVmnR1hZBfX0YNTXknNfQEEZ9fQShEGUecnIMSE/Xwu3WIClJe94JThgQ8DKGJtZnU18fRiSiID1dhzlzLCgsNA0I1MNhGQAHk0mA2Uz3t7IyiPZ2EXFx6t7XchyJE49Hi/Z2EUeO+KDV8ucNJqiEj0QAB72eR2Gh8Xx2hujpkdDUFIEkyYhEZLz7bitOnPCjs1NESooWWm0UyclaFBYae7M/M2eacfZsEEeP+hGNKnC71QiFZEQiCk6cIFMJvV5AfLwGSUkaGAwCkpPJGS83Vw+bjTYPnjPHjFCIfvHn5ekxaxYJl/7jA6iMMXY9QyEIHMxm6t+aOtUEnufgdqsRH68ZIJyo4iOKysrg+ZI/CaKoICeH+vOmTjUhK0t/fs8xNqcnBIJApUr3308ZpQMHKLhfswbweAb2fAQCFGy+/DKVTS1fToJiqIwJx1HgtHAhlcZt3EgiR5LIGry/+99geL0U2G7fTuVTa9ZQ4Nr/fDxPgd+0afT1+vV0DQDw5S+TiLpUmZKiUCnj+vVUTnXffTS2uLjBx2Yw0P1yuSjDsW8flWJVV5Nr3oIFtNIfu/7BCIdJ6H34ITX4P/wwNdnHjDwYl4fj6LnHx1PZm91Oz3L3bsqOAtQnd7k+tfJy4LPP6O+HHyax4XYPnDNuN80jr5fMV3btIpF2te6P0SiJ5Q0baOw330x/LBbKbul0NCfOniUTi9WrSYhcTU9fLFj5+GNyq0xIoAWRrKy+13g8NL9tNspQvf46larOmUOi9Gp7CGPlj1u30rxOSaHM1rx5w2u2wrgqmIBijBqKQmVUnZ0iWlrIPa+mJoTKyiAaGsLw+WTodDwSEzVISjIhPV2HyZMNSEvTQaNhq/LXQjgso7VVPO9kJ2DhQitmzjTDar24NE9RFGg0PBISNCgoMKKsLICPP25HTY0BBoPQ654XjcrgeaCqKgS9nkdeXp87nV4vYNIkHXJy9LBYhPNCrS/oUau5Xsvvzz/vgdcbhc2mwpw5FmRm6tHQEMakSbRHVyyLlJtrwH33xWH//h4oCuBwqBAOy2hqivQ65bndtI9XzEgkP9+IlSudKCoywWJRQavlMX26qddoIjlZe91ziuc5JCfrBvSI9cfvl1BdHcLRo37s29eNUEhGYqIWixfbMH++Bbm5hgHW7owJxvTpFJSuX0+ZEUnqyy7pdPR1XR2tkvf0UKBZXHz5AInnaQX6rrtIgG3bBvz1r/T9OXOGducLBGgfpp07KQh+/HEKMgcTJbHvxa5h3Tr6WZWKSqKSk4ceZ3Mz9b18+imJn/vuI2F0KWEnCBS433knZSO2bqXAfccOukd1dRS8OxwDxV6sz2rXLhKrfj+wYgWdU6NhmadrheNI5NxzD93jbdso26lWUy/bUM++oYGyVgcPklD52tcGt6nneRIi991HmdpduyjzuWrVxX1/QxEOU/ncn/5EYvuuu6gEsX+p6cyZNNfff5/eg3/5C83hrKwr24MsNr/276f5Jctk7DJz5sDXabUk9t1uOv/mzSTcqqvpPZ2be+UZNkWhfrR9+yj7p9PRZ8OCBUw8jTLstzXjCyNmOBAMyvD7Jfh8EhobwzhzhqyaKytDiERk6PUUtBcVmZCXZ0RJiRlGo4plmYaBSERGd7cIm02FwkIjFi+2ISPj4l8ctM8SCS6HQ4MHHojDX/7Sgo8/7sCnn3ZCpxMgSWTdzXEcjEbK0hQWmpCQ0FcKyHHAjBlmCAKHaFRBVtbAHimnU40pU0yYPNkAv19GTo4BS5bYMHu2GXFxgzd5WywqlJRYUVIysAdDFBVEIiSgtFq+d76oVEBmph4/+EHqgNcbjSpkZIzsR2DM+KSzU8SZMwF8+GE7Dh3ywe+XoFJxKCmx4L774pCczH4R3hBMm0YB1bvvUk+UolApUXo6BUn799PeSP/wD/Taq+nTsFgog2QykYB64QUKsGL9EbEgVFGo/OjQISoHslopk5Sff+XXYDRSEPzyy7Tqv3QplXgZjQNfGw5T9mH3bhJZ3/3uwLFcDpWKfu7RR8nZbONGCn4PHKAxz51L/x8ztRBFsnf/7W9JkD7wAHD33aznabhwuUjkGI3AH/4A/O53VMqZm0sCJPbhrihUirplC4netDTgyScpK3MppkyhTO2f/0x/nE4yrrhc5lAUqTT0gw8os/T971Pp4WDGCpmZlAmLiwN+8xuaJ1/5St81XIpolEThiy+SOP/Sl2gBYTBhzvN0jq98hQTWa6+RiNq3j94vCxdSNir2XhqMmEnF3r00Vlmm+zh9OivZGwMIzzzzzDOjPYiRYuvWrdBoNCguLobFYhnt4dyQKOetemm/NwWBgIRjx/zYtKkDf/lLC955pxV793ajtTWK7Gw9Fiyw4rHHEvDQQ/GYP9+GrCw9tNob23Z8OOF52hNJUcgZLiNDP6CvqT9ebxQ8z2HOHDNycw0oLjbD6aQ+KLWag92uxuTJBsyfb8FDD3mwejVZoMcyRTHsdjXy8oyYMsUIjhtYmka9QxqsWOHEbbc5cfvtDkyebIDRePVlNjzPQa3moVbzY2K+kHhS0NMjYf36VrzyShNOnvQjPV2HKVOMOHcujAULrMjLu7brZYxT7HYK1hITqTE/IYHK9Q4epKAxI4P6fq7EwvvCHZ61Wjp2WhplCf78Zwq2+u/hFI1SqdR3vkPCY80aEieDHTvGhQGi09nXq/Szn/U16yckDHxtVRUJxXCYepCGKl+KrezHfnawgNRmo0B03jwa///5PxRcJibSSj/HkRPaj39MLm/f+AZlIZh4Gl70esrYZGWROUpFBf3b4+l7brJMpajPPUfz+ZvfpEWCC+k/d2MkJdHzrK6mRYCpU2n+arWDz4vYfkgffQT8/OfAP/8ziZpLiTWDgd5zqanAf/4nLV6kpfXNo6HO09RErpeHD5Oxyx13XFmG2O0m0TRtGgm93/+eMnNpaSRKY2Ko/3ljZXsbNwK/+hX93//8D2W2WOZpTMAEFGNEkWWgtjaMPXu68fbbXrzyShM+/rgDJ074YbOpUFJiwT33uPD1rydi6VI7iovNiI/XsB6QEYLnAbOZStri4jRQqwe/z3a7GsXFJsyYYYbZTKVwJpOAjAw9ZsywYMECKxYssGL2bAsKCoxwuzXQ6a7dvIPjSJRRy8bEeO5+v4TDh3147rka7NrVBatVhQcfdGPFCidEUUFpqQ+LF9uQmam7SHQyJjhaLQWKWi0FUufOAWfOUCD4b/9GK+dXkqXp6aEA1unse31s5bu4mPpONm+mIC0tjT6QKypoFVulorK9RYsGt/QWReofamsb3HFPqyVTh6lTqeRqzx76fl4ejSEUomCzu5tKjkpKhl5pj0RI8KlUFNxeqqfKZCLxVlJCma1Nm6ikLxymvpQNGyiDt3jx9e2LxRiamAPfokV0z/fuJWGVnU332+cjswiPh8r+pk0b/NlHo/TsLxS5djsJL1kmG3WNhsT5YPPQ76eM7tq1VK65Zg39/OXeP2o1vc/mzqWs5uHDNPcmTRp8rI2N9LqXX6b36KJFgztjXgqbje7FggU07hdeINMMl4uur/+YZZlKDNeuJfH5n/9JiwXDZcHOuG6YgGIMKzH3vLNng9i5swsbNrTho4/asGdPNxoaonC7KTC/4w4nli61Y+ZMC3JyDPB4NDCZBOj1wvnNQtkHxEjAcVyvK50gDH2fyfSBnkcsayQIHLRa2ufJaKQ/er0ArZa/rmcWO/6F2anxTHNzBDt2dOLNN72orQ1j4UI77r7bhblzrdDpeFRWBnH4sA/LltmRkqKDTsd6+m4oYsYMsczTnj0kWO64g/o2rnQvp4YG6sV4800qwbPZ+jYZs9vJ5vzUKXIlq6khB7JXX6XXfO1rJEKs1sHPJUm02envfkfHcjovNpfQ6SgITUqi1fm9e2mFPT2dyqn27qUAdeXKoR37Yhuy+nzUH9bdTQLQYLj4tTFrUKORzpuVRfexrKzPHOCxx8hxLbZf0UQjGKRA/uhReibDYcfdn717aa7wPJWFDgbH0VxwOmkOl5VRtlGno+f8xhtUjnr//SQWBhujLFN555/+RPPHYukTLioV/Uxqat9Gux0dJDT6Z5ZCIZr7W7fSnPva10iIXIlRSGx/C7ebzl9ZSWNua6MyP52u730RCNAiweuvU9/iypU0jqs1JIktELhcNN60NJqze/ZQr2BCQt8937SJyhHtdrquyZOH1w6dcd2wHijGsNDREUVtbQgVFSFUV4fQ3BxFXV0YigLYbAIKC41ITdUhPV2H+HgNEhPJFW0slFoxGMNJXV0Y27d3YMeOLnR3S7j7bhcWLLAiI0MPo1HAuXNB+HzUO2axqC5y/WPcIAgCBVCrVpGAiI8n8XSlG7y2t9MGnqWlFFTv3ElBbVJSnzvftGlkdfzBB8CRIyQ8EhLImWzRoqHFk6JQQHnwIAmijRsp2zV9OgXNMTiOjjF/PgmZrVuBzz+njNqxY1RyN38+ZSIGw+ulALK7m5z1MjLo5/x+GuNQP8fzdN65c+m+paVRBk+vp4yH2z14cOv30z0az5votrVRwF1TQ1/fd9/l3RavhupqsgD3eOjZxRwPLyQmoOfPp0zl+vXUU9fQQD14S5eS/Xn/+dL/HAA9I4OBrL7vuouES0w46/W0APDgg/T18eN9P5OVRXN+3TrKXLrd1O92tbbkPE8ZzUWLSNxs2UKirquL3jcJCfT9Q4fIBMVqpQzXhS6CVwPH0TXm5VFGKT6e3rt799L7Zt48Mtp46y26BytXUpaXCacxBxNQjGtCkhT4/bRPU2MjWY+fORPstWd2OmnD1OxsclDLzNQhMVELtXoCrggyGABkWUF7exSfftqJbds6IUkKbrvNgZUrHbDb1b2mFpGIcl5AodfinXEDs2QJBXFqNQmIK6GlhYK648cpwE1OJgFhNlNg1795/qabSDAcO0Z/z55NzfpDZWcUhWzD9+yhFf477qAekQMHSOgVF1/c66TXU+DndlMmaPt2ElRLltDK+WDBX3c3ZVE+/5wCYrudelfee4+uRRAosB1KDAF9wXR6OpXwyTLdywvPJ4qUITtxggLX1NRBDzemkaQ+8SQI9KxPnCAXx1mzrjxrORShEN33hgaaA/X19Bxjz3yw3qDYXmfLltHPbdhA4igcJkEUE/MxZJmuYedOEmiFhSQWYvuLBYPUwxcr1RMEKqn78pcpU3XsWJ9Ff2Ul9T15PINvyhy7Jp+P/r6UfbjBQILd5aL5F3PJXLqUMkLbt9P9eOABGs9wwPN9cz4lhTJOBw7QogLP07hXryazCdbHNyZhAopxRcQc9AIBCT6fjK4uEbW1Yezc2YHSUh+iUeX8fkBqzJ5tQXGxCVOnGmEyMfc8xsRHURREozI++6wLGzfSxrx33unEqlUuaLUDf2lHIjICAblXQLH3xw2O1UqB2uWINdy3t5OT1/79VC719NMkVl55hbJMPE/CJVY2JQgUhC1cePnjxwLnTZtI4MybR4GlLFMp3+7dlMWJCZv+wbEg9BlYrFhBgXJOzuBlYKJIWY6DB2m8d91FAkCvp6Bx61b6I8t0/gvtyi9EpRo6IxCNUnnU5s10Todj/AmomPHHzp1USrZ0KV3DZ59RWVlcHAXhQxktXAqqu6dM4Jtv0n2+7z7Kwnz8MWVCTKY+u/3Bjm800nNqbqZs5cMP0zzo7xQny32lcLHyQ4eDxv7008Czz1KpniSRsDKZ+n42OZkyQm+8QQLn9GkqTS0poXPNmHHxuEIhyuhUVdE1eTyXLunkeRKKcXE0t198kUS3Xk/iMDeX5ulww/O0YXZGBi12vPUWvY+/9jX6mrWfjFmYgGIMScxBjwySFITDCvbt68aOHV04dMiHxsbI+QUiHUpKrJg/34rcXD1MJjatGDcWoqigrS2K3/++CbIMPPqoB3fc4bxIPAEkoHw+6fweWExAMa6AmLiRZSqTOn6cgsf77+8TDo8/TiJq/37KCtx669COYoMdX5ZJHP3Hf9Aq+91395VvCQLwxBMUvG7ZQlmGJ5/sK4Xrfw6djswEsrMHPw9AbnmbNtHPffe7A8WRwUAbCLtc5OIWDFIWLD7+2sRBczNlxd57j65t8uSrO8ZoE7uGd9+lP88+S4JBo6EMRk8P8F//RSIkI+Pq7lHsuR87Brz0Eh3vBz+gDCNAGaT16+nYzz9Pgnio/bQmTwa++lUqq1ywYKClfcxRrrycTBi+8x16Tey5WyzAv/878NOfkgCLREjw93dlTEuj/raCAhLyjz5K2dTBjCUUhcxS3n2Xeqf++Z+vvF8pKQl45BEqV/3JTygbdeutNAdHMhNkMlEmcdaskTsHY1jhFKW/V+nE4kc/+hFMJhMeffRRJF3ppmWMXmRZgdcbxcGDPdi3rxunTgXR1SWC54HERA2Ki02YPt2M5GRtrwGERsOxvibGDUd7exSbN7fjN79pxIMPxuH2251ITtYO+l7Yt68br73WjMbGMH7721zYbGpW3s64NLH9YJ5/nlboly+nkqX+LmCKQlmDDz+kzM7NN1Np1ZX0akQilIH44Q8pu7FsGQXjF9ol+3wUbO/aRSLoBz+gLNiV9oPIMmXQfvELCtJvu436Vi7MDFC5AwXBv/kNlenddtvVi5/KSsqiHDoEfO97156lGU1OnqTsWXV132bHsX2volHKGL76Kv377rsv3tT1UkSjdH+2b+8TzS5X3/OMZe927ybjii99qc99bqjjhcN944vd51CIsirPPUeW5rNmDXTKiy0QtLf3lXBOndrX/xQ7jijSsYJBOodON7gwOnaMsmkWCy0ypKRcXZ+YLNN1tLbS/bVaqUz0SjbbZdwwsFQBo5dYpqm6OoSTJ/04dSqImpoQ2tqi8PkkJCRoUFJiQWamDsnJWjidajidauh0zAyCcWMTjVIGSpIUeDwa2GyqId8TkYiMcFiGyRRzOPyCB8sYX0SjJCTWrqWAcMECygxdWNoTM3RYuJCCxW3bKOCbMePSTm2BAAmu994jkXLzzbTaP9heMyYT9U+p1dT0/n//L/Dtb1OAernVeUmissBf/ILKpObPpzK0wcqqYo32OTmUddi0iYwwuroG73UZjLIy2sS1rY2yFenp198n9EUiSVSyd/gwPcdHHqH70d/GOmYa8uCDlJn87DMSFNOmXf744TDNqYoKEivz51+c5YuVvt10Ez2nvXvpGSxdSmVuF6JWXzwPolGaXxs3Uq/S9Okkuvs/95jYcjr7+o7KyiijumZN3ya9KhXNwf7lfRdeU1kZOVMmJdF7ITn56t3yeJ7OmZzc5+Y4no1HGCMCE1A3OIoC+HwiGhsjqK4OoaYmhNraMGprwwgGZVgsAvLzDUhN1SM5WYO0NB3cbs1VbfwpywoaGsKoqwsjKUmLxEQNBGHwWmRZVnD0qB91dWG43dRPxWCMdbRaHqmpOqhUHM6eDSI/3wiLZfCP12hUQSQiw2gUxk0sxxglolHqF4k57C1ZQnblQwWQHEfN8vPm0Ur9xo0UPBYVDV7q1NNDJUqff04i6M47KWC+lBgym2kMWi0FrO++S+fLzx/8HACt6Le2UhaD46j8MCfn0huCxjYGnjGDznPgQJ/de0nJpcsTT57sMyVYsIAyHuPFAlpR+jJDJ0/2uQ0O5YanVlNmbulSyhQdOEDiMzd38NdLEonm99+nHqHs7D4xOxgqFYmlm28mEXH2LJk3LFx4eUMFWSaXyL17KbN1xx3U9zSUoOE4moeCQNd1/DiJvFtuoXl5KSHk91OJ4Pr1JAQXLKB7cK1uebHx9O/jYjD6wQTUDYgkKQgGJXi9UXi9ffbjZ88G4fVGYTYL5/dr0iE314DcXANSU+lD5Fp+/4TDMo4f92Pnzi7ccosdbrfmos/BWCFpeXkQGze2obo6hJISKxNQjHGBwcCjsNCISZN0OHLEh0mT9PB4NDCbL/6IFUUFkYiCuDgmoBiXwO+n1fR9+0gI3HknBcqXCwh5nlbfV6ygDWZjWYkpUwZmrTo76diff06C7J57SHxdyaQ0GGgsTifw+9+TwAsEqAl/MNvq1lYK7A8fpoxCQcHQIrA/sbHMn0+B7J49dD0c19cH1H+80SiVun36KWW75szpy8iNBySJnvuePfRsUlJo/FdSujh7NonmQ4foeWg0lEnsf+2iSGVy27eTg9/MmSTOhrKLjxHLDt1+e59VvSjS95OShhbcFRV0HZEI2fUnJl7ZfUhMpFJBg4HKFzmuT+QNNv+7u6nsb9cuGssddwz9WgZjmGCz6wZBkhSEwzL8fgldXSLq6sIoLfXh+HE/vN4IOI6D06nGnDkWTJ9uwrRpJjid6msuzVMUBbIMhEIyvN4ITp8OoKzMjzlzzLiw605RFEgS4PVGsXatF6WlPUhO1iI19RKrkwzGGEKj4ZGYqMXy5U68+WYLSkt7kJamRXGx+SKTCFFUzrtW8hNm42DGMBJzRTt2jDJIZjP1nlyNfTLP00r/d79LfVMxEVVcTAFmIECCZuNGsvW+//7Bhc+lUKupj+nJJ8mxLGZ5PWcO9bfE8PlIOO3eTUFxcfHgm+RejhkzqPRryxbgj38kAZaRQcfieQrSm5qoFNHrpX6eGTPGl3jq7KSM45/+ROVuixf3GTpcDo7rE4tbtlAv3AMP9PWoxZz8Dh6kfZqefpqexZUI2RgaDWWDrFYqkwuHKfN1YW+ZopCo2bSJnsuiRTTPrgabjX5OEMiZLhSi3r/ExIHCKBCgTF2sXPNf/qWvB4vBGEGYgJqgXOgN4veLKCsLYOfOTuzZ04OamjA4DkhN1aKkxIrFi22YPdsMjWZ4ftnIMpUGHjniQ0eHiNbWKLRaAUlJugHZJ7JHV9DTI+LXv67Fvn09yM834L774rBo0RA71zMYYxC1msM997hw4oQfe/d2QafjkJmph9VKq7N9fdAyolH5vIAaxQEzxh6x8q1jx4Cf/5zKpu6/n8qfrpZYH8cPf0jN+x98QIFvSgqJp5deImvo5cuvLojuD8dRVus736GgfMMGsnx+7LG+CX/gAJVwJSTQtVwPmZnk7qbRAP/4j8CPf0wiQKMh8bRuHQmQH/1ocHOKsUpMcOzaBfz3f9P4Z868egtrnqdMjcEA/M//0PO+7TYS0zHnw3XraD5kZFxbeZpGQyWUSUnAv/0blfTF3PFiiCKJuKYm6p+aN+/qzxM715IlfZnOxkbquesv9o8fJ7EoisAzz4w/kxDGuIUJqAkK9TZJOHbMh717e3DihA8tLVGEwwqMRgH33uvC4sU2JCRoYDYLMBgEqNXD+6HT2Sni7bdb0d4uIhSSeveJuvB3WnV1GK+91ox9+3pQUGDAvffGYcaMSzQ9MxhjFEEAVq92nV888OOdd1rx1a8OXEGWJMpC6XTjJLhjfHF0dNBK+l//SvvbzJ1LK/HXg0ZD7m3vvUcGDllZVOL11FOUobmWbNCFqNVUYuh2U5D+T/9ErnfnzlE5ms1GYm04cLmoPNHlIve51lZq9N+5k/79L/9y8QauY526OrpvMeEcy6xdCxxH2Z6nnqLnrSj0zEtLqbzx2Wfp+NdripCQQILl3XdpL6qlS0nw+3xUtrdxI5lbXKnpx6XIyQG+8hUq53v+eRLs8fH0zLdsobHcey8zemB8oTABNXb58R0AACAASURBVMHweiMoLw/i6FE/yssDaGuLorU1CpdLjZISK7Ky9EhO1sLj0SAhQTNiDno8DzidGtx9twsHD/pw6JAPBoMAp1PTW7YUjco4etSHDRvaUFpKmad7741DcbH5qkwqGIyxQGxeZ2XpMX++Fd3dInbv7sKUKUZMnWqEVitAlhVIEpW3ajQsA8XoR3Mz7eH02WckNmbPJpFwtQ5iFxLricrLo1Knzz8HvvWtvpK44cjSxBwAZ86kDMCuXcD//i9lDKZMoeD6aksEh0KlomPNm0flYZ99RsIpNZVKHVNTx49hBEDPZOtWMvRYvZr6nYbaa+lK4DjKPObmAn/zN2TCsHUrPf977rnYye9az6HRkEvdypU0b0tLgZoa6rtau5a+f7UlgkOh0/WZYuzeTRm0mTOp7yk7mwwjrmWfMAbjOmACapwjSQoCAQmnTgVw9mwQ9fVh1NSE0dwcgSBwSEvTYdYsM9LT9Zg0SYekJC2s1pF/7BzHwWQSMHeuFS0tERw/DlitQu/Goj6fiNLSHmze3IEzZ4KYOtWEZcvsmD7dPKR7GYMxHjAYBMycaYbXG8GmTR145x0vPB41EhKopy/We80E1A2OJPWJpvZ26t84e5bKnlJSgJaW4Q0I6+upB6a1FaitJXEzEhMwEKBzlZWR5TVAouqzz4b/XK2ttL9QbS3dw4QECuQvxZQpJCKuN7N3rXR2Usapu5u+3rGDxp+SQnPicuO/UmKb5FZV0b9zc6ln6fPPh+f4/REEuq5jx0i8RaMkdM+coTk9XIRCJKZi88vjoWxaczO9XwYj5qRXWDi+hDVjzMMi1XEI7akYRWeniPZ2EVVVQRw40IPTpwMQBDKDyM83YvJkPfLzjcjM1I/aXk16PY9QSIYkKbDbVVAUBe3tIg4e7MEHH7Shvj6MoiITVq1yoqDACJWKlTUxxj9JSVrMmWNBVVUIn33WjalTTVi61A6LhbJQHMdBrWZ7QN3whEIUDDY3U/DscNBKutc7/OcSRQo2J0+mc44kLheVboVCJJ5qa0fuXAUFtMeTolDJ4OVISqIAf7Tw+WiD38ZG+rqxke6X1Uo23MNFrJ8uMZFKHI1G4PTp4Tv+hbhcJJjr6igjVFtL/XDDjShS9nTbNspEdnZSH9SlsFppnlxvNpfB6AcTUOOEmFOdzyeiq0vCkSM+nDoVQFVVCOXlARgMApKSNJg+3Yw5cyzIytLDYBj9DwsyiJAgioDJJKC+Poz9+3vw5pstCAQkLFliw733upGWxvZaYEwceJ5DdrYBK1c6ceJEAG+/3YrkZB0KCgyQJAUcx36X3/AIAgmav/3b0R4J44vEaKRsk9FIX2dljez58vNH9vgXnismmtXqkTPxkGXa2ywYpF4xvf7SrzcYWPaJMewwATVOkCSgtTWKTZvasGFDG+rrI+A4IDlZi5Urnbj5ZhuysvTQ68dWVCaKCnw+CYoC9PRI+OUv67BnTzccDjUeeSQey5c7vpCSQgbji0av5zF5sgFf/rIbL7zQiHXrWsFxrl4b//FiEMZgMIYRm416gxgMxriGRa5jGFFUcPp0APv3d+PIET9qakLw+SQ4nSqsWuXE9OkmZGWRTbLJxJ/vqRhbKywtLVH09EhobIzA5xMRCMiYNcuMBx6IQ0GBEWazasyNmcEYDjiOg9WqxuLFNpSW+nDiRADbt3dCFGUAgErF5j2DccPBft8xGBMCJqDGGD6fiMrKEM6cCeD06QDq6sJobxehUnGYPNmAggIjUlO1SEjQIC5ODZNJddFGnWOJY8f8aGiIIBCQEArJkGUFDQ1hnD4dhNOphlbLj4lSQwZjJFCpqCfxoYfi8fLLDThypAeBgAxB4MbkggeDwWAwGIzLwwTUGECWFTQ1RXD2bBCnTgVQWRlCQ0MIoqjA7dZgzhwL0tN1SE/XYdIkHcxmYdyYLVRUBNHaGoXDoUJKihaCwKGrS8SOHZ2org4iN9eIvDwDsrL0MJsFFlAyJhyCwKGgwIhVq1xYv74Vhw/7kJCggcejZovRDEY/AtEABE6ARtCw3wXXSG1XLdqD7ciPy4eKZxUeDMZI8YUIKFmWIUkSOI6DSsU0G0B7IHV2imhpoX2azpwJ4OhRKtMzm1WIj1cjN9eIwkIjsrP1cLnG5wZxbW0RAAqKiky45RYbBIFDbW0Yp08HUFERQnl5CCdO+DFzpgnZ2QYkJmphsQhQq8eHQGQwLgd97gGLFlkhioDdrobVKiA9Xc/K+BiMfuyt24tQNIRMRyayHFkQeFadcLUcbT6KA/UHYNPZkGRJggC2MMlgjAQjrmZkWUZ9fT1aWlrAcRzMZjP0ej2MRiOMRiPUavVVvbmV8x3Y4/EDQZIUhMMy/H4JXm8UJ074sXdvN86cCSAaVWC3q1FcbMLChTbMnGmCyaQatwGWoigQRQVdXdL5TXwtWL68byPFtrYI9u3rwfbtnTh2zI/S0m7k5RmxZIkdBQUGuN0a6PU8E1KMCYNGI2DpUjsWLbJCURQYjWwxicHoz/tn3sfhpsO4Kf0mPFb8GFIsKQDG5+/74UZRFIiyiKgcRVSKQlIkyIpM3zv/tSRL2Fu3Fx+Uf4AkaxJWZK9AnCEOakE92sNnMCYcI/4bPBwO49lnn8Xvfvc78DwPh8OB2bNnY/ny5Vi2bBkyMjIg3CB+vn6/hIMHfdi6tQP793f39jbNnm3G4sU2zJhhRnKyFhw3/vtMZRlobo6gvV2EzaaCxzPwA9zhUOO22xxYvNiG8vIg3n67Bdu2deKzz7pRUGDArbfS/yUmakfpChiM4UcQyJ2PwWBczNNzn8Yrh17Bp+c+RXugHT9d/lOoOLbQAACyIqPZ34yqjirUdtXCG/CiI9SBZn8zarpq0B5sR7OvGc2+ZgTEAH609Udo8bXg8WmPI8GcMNrDZzAmHCP+yaTVavHYY4/B4/GgoqICGRkZ0Ov12LJlC9566y0UFBRg1apVWLx48aDZKEVRoCgKTpw4gT179mDPnj2Ij4/Hc889B2Dsr0z5/SJOnw5i795uHD7cg6amKERRRnKyFg8/7MaMGWZYrSqYzSro9fyYNoS4WqJRBYIApKfrkZo6cJ8GjqNNRPV6Hrm5enzrW0lYvToOn3zSidLSHrz+ejNOnQrge99LYb1RjAkDm8cMxtB4TB48Mf0JeEwerD+9Hs988gx+uPCHMGlM4DDx3zuxLFNFRwVOek/iXOc5NPmaUN9Tj/K2cviiPsQZ4mBUG2FQG2DSmmDT2lCSXAKH3gGrzoqPKz/GX479BXqVHrOTZsOkMY32ZTEYE5IRF1A8z2PKlCmIi4tDV1cXzGYzFEXB7NmzcfLkSZw6dQqvvPIK3n33XeTl5cHhcEAQBITDYfT09KCtrQ21tbXo6uqC0WhEWloaSkpKRnrY10VdXQg1NWFUVARRXh5EU1MEXm8ENpsKM2eakZOjR2amHsnJWrjdavA8N+ECK44D4uLU+PrXE+FwqOB0Dl5CwPMc9HoBOh0Pl0sNm02F5GQtSkt7WPkeg8Fg3EBoBA08Zg+WZy6HpEh4p+wd/HLPL/GVoq8gzZoGfgJtniYrMvxRP862nUV5ezlqumrQ6GtEs68ZYTEMm94Gg8oAvVqPyc7JmJE4A3GGOJi1ZugEHTSCBlqVFjqVDka1EXq1HmfaziAiReAxefBA/gMoii+CXn2ZTWYZDMY18YXkxk0mE0ymgasgOTk5KCgowPHjx3Hw4EHU1taiuroaNTU1AKh3CqAVW6PRiNTUVEyaNAlTpkxBTk7OmBIcoZCM9vYo6urCqKwM4dy5IJqaomhri0CSgMREDQoL7Zg0SYf0dD2SkjSw2yd2TTLPczCZVJgzx3JFr+c4DhoNh0mT9DAaBaSn6yBJCrTaifMLk8FgMBiXhud4pFpTcUfWHQhEAthVswvBaBCL0xZjWsI0xJviR3uI14QkS/D6vTjXdQ41XTVo9jWjJdCCsBhGKBpCSApBURTYdXa4jW6kWFPg1Dth1Vnh0DvgNrrh1DvB8/yAbJyiKBAVETurd+Ljio9xynsKHpMHt2XdBqfeCRXPSiAZjJFgVN9Z8fHxiI+PR0lJCWpqalBeXo6Ojg5Eo1FoNBpYrVbEx8fD4/HA4/FAqx39fhgqKQS6ukR0dYno7JTQ0hJBdXUYp075cfp0EGo1B7tdhfR0HbKz9SgsNCE/38D2fblC3G4N3O7x6TrIYDAYjOtD4AWk2dLw9RlfB8/x+PTcp/D6vajtrsWMxBnIcmTBrDGPi9+niqIgLIVxsOEgDjcfRlVnFdoCbegJ90CURUyyT0KGIwMekweJ5kRk2jPhMXmuyIEwKkXREezAgcYDWH9qPXrCPdAKWpi1ZqRYUyZUxo7BGGuMiaUJg8GA3NxcpKenQ5ZlaDSaMWF3ft7wD9GojGhUQSQiIxyWEQhIOHkygLKyAM6cCaKxMYxIRIHBwCM1VYcZM0yYOdOMzEwdTKbRvw4Gg8FgMMYTPMfDprPhe/O+hxmJM/Da0dfwyqFXsKtmF9ZMWYMCdwFcBhe0Ki14buwKBQUKukPdePnQyzjRcgLZzmzclH4TZifORq4r95r2vFIUBSExhPrueuyt34v/2vdfyLJn4WvTv4ZDjYewpWrLCF0Ng8GIMWai+2g0irKyMnR3dyM7OxtJSUmjPaReamvDOHMmgFOnAigr8+P48QBkmTJR6ek6zJljQWGhCfPmmWG1qqFScRPCSY/BYDAYjNFmUdoiTPdMx6fVn+Llgy9jzTtrsCR9Cf5+/t9javzUMd/no1Vp8cjUR+AxepDpyATPUTXKtRpjKFDwecPnePHAi9h6biuenvM0vlz0ZSRZknCi5cQwj57BYAzGmBBQiqKgo6MDzzzzDIqLi+FyuYZdQMky7UsUDsvQ6YbeX6irK4rGxigqK4M4dMiHioogurslhEIyAAVms4BFi6woKDAiN9cAl0sFo5Ec9IxGAYLAnLYYDAaDwRgueI6HSWvC4rTFyHXm4lznOWyp3IIfbvkhMu2ZWJGzAovSFsFlcI32UC+CAweTxoSZiTOh5tXXvSfT4cbDeLPsTZQ2lCLZkozXV7+OgjjKxsWEGYPBGHnGhIBqbW3Ftm3b0NLSguLiYiQmJg7r8RUF8Hoj+MMfmpGaqsXChVYkJ5NJQSAgoaYmjKqqIM6eDaK5OYrubgldXSLa26OwWlWYPDnmmKdBXJwadju5yjkcamg0E89Bj8FgMBiMsQTP8bDqrDBrzEi2JMNj8mBm0kxUtFdgc8VmbK7YjFmJszA/dT7SbGnQqXRjwvqc4zgInHDNduIKFPSEe3Ci5QS2VG7BydaTcOgduDvvbkzzTEORm5z2WBzCYHyxjLqAkmUZdXV1WL9+PRYsWIAZM2bA4XAM6zkiERktLRFs3NiOkhIzdDoehw750NoaRSAgo7ExjKamCHw+CYLAwelUIz/fAJtNhcREDdLSdPB4NLBaVTAYboxNfxkMBoPBGGvwPA+jxoipnqnIj8vH6bbT2F+/H2fazuCE9wROtZ6CTWdDojkRk2xk0JBkSQKP8ZWdCYth1HXXoay1DGXeMtR21UJWZKTb0jEvZR5mJc4at46EDMZEYNQFlM/nQ3l5OU6ePImnnnoKLtfwpOAlWUJErUd9B4/PD/WgzcvD75fQ2BjB5s0d6OigTJPJJMBsFmC3q1BQYERiohZpaTpkZuoQF8ec4BgMBoPBGIuoBTWmuKcgz5WHJl8TdtTswJaKLShtLIVOpUOGLQOT4yYj1ZoKt8ENs9YMs9YMu85Om/OOEUGlKAoC0QDagm1oDbSiK9SFtmAbarpqcLb9LJp9zXCb3Fg9eTWKPcWw6+xQCaMevjEYNzSj/g6srq5GWVkZMjIyUFRUBKPRCIA+UKLRKHp6ehAMBiFJEjQaDSwWS+9rLkU4GoTPEI/dh/w4crwWQrgHgIAzZ3ywGTmkJKkxY54BOTl65OYaMCldf74cL3YEGQiFRuy6GYwbCkEA1BN77zMGgzE6CLyAJEsS1kxZgzVT1qC0oRTbq7fjlPcUNp7ZiKrOKkxxT0GKJQWT7JOQH5ePdFs6tCotNLwGOjVtTKvm1RftszScKIoCWZERlaOISlGExBAiUgQhMYS67jocbj6M0oZSVLRXoC3YhlxXLpZlLMPfzf475MXlAcCYKEtkMBhjQEBVVVWhqqoKt99++wDrclEUUV5ejjfeeANbt26F1+tFYWEhHnvsMdx1112XPW4k4IMSMSMaUKMrEoIi1EKHdGSlBfHtFWpMz1DACxFwXBf4CMCVj+RVMhg3OHFxQFraaI+CwWDcAExLmIai+CIoUBAWw2jwNeDTqk9xrOUYPij/AL/a9yv4wj7kuHKQbc/GgrQFyI/LR6Y9Ey7jyBlRyIqM9mA7KjsqUdVRhR3VO3DCewJn289C4AXkxeUhz5WHeVPn4eZJNyPZnAy1oL6iPaEYDMYXy6gLKK/XC6/Xi1mzZg0QUE1NTdi5cyc2bNiAiooKFBYWoqysDHv37sWSJUtgNpsveVxTRS2iurch5RyBozsbgvdmBJCOz7RvoPNUGRafBEq6rZgcMMApspVxBmNEmTsXWLMGsNtHeyQMBmOCw3M8eIGcdlW8CunWdKzOW43bs29HSAyhM9SJ6q5qnPSeRFugDZsrNuN3B3+HoBiEU+9EliMLLqMLHpMH8YZ42PQ2OPQOuAwuGNQG6FQ6aAUteJ7vzSpFxAhERURXqAudoU50h7vRHmxHXXcdmv3N8Pq9qOqoQrO/GSpBhUnWSchx5mB13mokW5KRZE6Cw+CAXqWHTqWDRWu5pj2iGAzGF8OoC6hQKASfzwdRFNHV1QWO46DRaGA0GuFyuRCJRFBSUoKamhq0tbVBURSor6AUSJWSCskqI2pvhzVOj0m2adjXBkzyJKFWdwCvByvwkQpwG/VI1DqRac9EpiMT2Y5sJJgToBO0X8DVMxg3CAkJgH5s79XCYDAmHjzHQ6vSIk4V1/s9URaR7chGobsQvogPHcEOtAXa0BXuQk+kBz3hHgSjQZS3leNgw0GEpTBkRYYsy5AhQ8WrIHACOI6DAgWKokBSJCiKAg4cBF6AWlBDw2tgUBug4lVwG93IcmTBorXApDHBoXfAY/LAorXAprPBpDFdt8U5g8H44hh1AZWQkACn04nXXnsNFosFHMchLS0NkydPhiRJMJlM+PrXv46f/OQnSElJQXZ2NjSaKzB3iI8Hp7IgJPPQ6YHpdgP2A5iXtBC6HDsa5ZOo6apBlb8Fx6N+6FT1SDDJSLNEkGzpQpI5CYnmRMQZ45BgSoBFa2EfbgwGg8FgjHNUvAp2vR12fV9GXJZlhKUwOkIdaPQ1ojNIWaTWQCt6Ij0IiSEEIgFE5AgiUgSiLEKBAoD6klS8CipeBb1KD71aD4PaAJPGBJfBBZPGBLvOjgRzAlx6FzSqkTOoijfGI8+VB7Pm0lU6DAbj+hh1AVVUVIRbb70Vn3zyCSorK8HzPCKRCERRRGtrK9xuNzIyMuByuTBr1izMmDEDPD/4JrgXoo6oEQ6GIOsakCzWAshEhiUbt06dDc7UgbPtZ3Gm7QxOtZ1CRXsFWv2tqOqsQkSKwKq1ItmSjDRbGnKcOUi2JMNtdMOpd8Kms8Gqs/auQDEYDAaDwRi/8DwPPU/iJ9E89F6UiqIgKAYRkSKQFRkcOPAcTxknQTPqccGU+ClwGBxw6B3McILBGEFGXUBlZWUhKysL3/rWtwZ8/9NPP0VZWRmSk5Px8ssvw2g04pZbbsGUKVOu+NhCVIAoAQE+gijIUS8aVaDIQKI5AQnmBCxMWwhFURCRIjjbfhZHm4/iUNMhHGk6gtKGUuyu3Y2wFIZFY0GOMwczEmdgmmcaprinwKK1QK/WQyNooBW0UAtqcGAb6zIYDAaDMRHhOA4GtQEGtWG0hzIo+XH5yI/LH+1hMBgTnlEXUEPBcRxaW1uxZcsWWCwW/PznP0dJSckVZ58AQBVRQRAFRBBBN98FAAiHFcjyxa/VCBpMdk3ubeqMSBH0RHpwtOko9tbvxeGmwyjzlmF79XYIvACe41HgKsC0hGmYljAN0xOmY4p7CvQq1ufBYDAYDAaDwWBMVMasgCoqKsKTTz6JJUuWID8/H5MnT4bZbL6q7I4gCuAlHhInIioEAAChkARRVAa8LnZMgRMggOxCNYIGerUe81LnochTBH/ED1/UB6/fixMtJ1DmLUNVRxW2V2/HpopNMGqMMKlNyHRkIs+VhwJ3Aaa4p2CSbRLrnWIwGAwGg8FgMCYIY1ZAWa1WFBUVIT09HU6nE4IgXFX2CQB4mQcv81A4EaIQBACEQjIkSbnMT5KoUnEqWLQWWLQWAFT7HJbCyHPloTXQitZAK7wBLxp6GnCu8xxqumpQ112HU62n8NHZj+AyuuDUO2HX2XtFVY4zBw4Dq01mMBgMBoPBYDDGI2NWQPE8D4PBAIPh2uuMOYUDp3BQOBkSHwXPA5HI4CV8V3Q8joNOpUOKNQUp1hQA5NzTFe5CbXctGnoaUNtdi9quWtR316PB14DShlL0RHqwQ78DOc4cZDuzke3IRqYjE2nWNLiNbvAcz/qmGAwGg8FgMBiMccCYFVDDgtLvL06GRsMhGpUhy5fPQF0pPM/32qEWxRcBoN3GG3sacbL1JI41H8Nx73FUd1ajzFuG0sZS2HV25LpyMc0zDRn2DNh0tEmf0+CEVWdlfVQMBoPBYDAYDMYYZUILKIVToHDnN7bjeGi1PKJR5YpK+K4HnuORZElCkiUJSzOWQlZktAXbsK92H442H8W++n3YVrUN7595HyExhBRLCmYkzsCC1AWYljANiaZEcvZTaaFT6aDm1RB4YUTHzGAwGAwGg8FgMC7PhBZQMTgAKo6HTscjElEgSV/0+Tk49U4sz1qOpZlLEZWiaPI1YWf1Tnxc+TF21OzA22Vv452T70DgBRhUBhTGF2Jx2mLclH4TCtwFcOgdX+ygGQwGg8FgMBgMxkVMbAF1vq2I4wAVOKhUHCRJgTKyCaiLh8FxtNmewEMNNbSCFmm2NNh1dixMW4iucBe6Ql2o7KjE542f40jTERxpOoLTrafxxok3YNaY4TF5MCtxFhamLURRfBEsWgt47upMNRgMBoPBYDAYDMb1MbEF1HkUAAoHqNU8JAnD2gN1LXAcB42ggcvogsvoggIFUSmKwvhCzEyaiaaeJjT7mtEZ7kRlRyVOtJzAiZYTOOk9iU+rP0W8MR4plhTkxeWh2FOMHGcOtIKWGVEwGAwGgzEMKIqCyspK1NXVISkpCVlZWSN2rsrKSuzbtw+HDh1CV1cXNBoNnnzySeTk5IzYOccie/bswc6dO5GSkoI1a9ZAFMXeZ5CZmYm0tLQBr9+9ezd27NiB7Oxs3HfffaM06ksjiiI2bdqE0tJSLFy4EEuWLLnuYx49ehQ7duyALMt46qmnrukYH3/8MQ4cOICpU6dixYoV1z2mG5EJLaA4hTI/igLIvAJBGJ0M1OXgQILKbXTDbXQDHvq+L+JDdWc1TrWeQnlbOep76tHoa0SZtwz76/cjrjoO+e58ZDuy4dQ7keXIQoI5AfHGeFi0FiaoGAwGg8G4Ro4ePYqtW7di0aJFIyagQqEQPvnkE3zwwQcIhUJwOBwQRRHytdoFj2Pq6uqwc+dOFBYWYs2aNYhGozh48CC2bt2Ke++99yIBVVNTgx07diASiYxZASXLMg4fPox169bB5XINi4Bqbm7Gvn37IIriNQuo48eP47333oOiKExAXSMTWkBR6glQoECCDEHgIMtjT0ANhUljQoG7AAXuAiiKgpAYwum209hbtxcHGg6gurMapQ2l2FKxBVpBiyJPEXKduchx5vSWCJq1ZsQb46FVaVnJH4PBYDAYV0hNTQ327NmD1NTUETtHR0cHdu/ejcbGRnz1q1/FwoULoVarkZiYOGLnHEsoigJFUcBxHFJSUrBo0SKkpPRtE1NZWYndu3dj7ty5F/1sWloabrrpphHNDo4V+t8nj8eDkpISSF90Qz9jABNaQMX2gZIhQ4QEQcC4EU8XwnEc9Go9ij3FKPYU45v4JtqCbTjSdARbK7fiaPNRHGw8iG1V2yArMuIMcSiML0RBXAFuz74dSeYkGNQGaARN75/YcRkMBoPBAKjkKBAIIBwOQxRFKIoCnueh1WphNBqhVqt7f28oigKfz4dgMAidTgdBEOD3+yGKInieh9FohF6vh6IoCAaDCAQCkGUZKpWq9/94fuDCXjQaRSgUQiAQ6A0Q1Wo1DAZD7zlidHd3IxKJQKfTwWQyDThOT08PwuEwtFotzGYzAPSOVa1WQ61WDxirTqeDwWCARqOBJEno7u7uPX5XVxfq6+sBAIIgwOVyQaUaOnwSRRHBYBDBYBCiKA56DbIso7u7G6dPn0ZLSwscDgfy8vJgtVqh1+uh0WiGPL4kSQiFQr3Hl2UZPM9DrVZDr9dDp9MNuK+SJCEcDiMQCCAajfYG4iqVqne/TVmW4fP5EAqFBjyz2LFjr+t/3Yqi9M6XUCgESZJ6j2symaDVanvHIYpi7/FNJlPvNUiSBLVaDYfDgaKiImRmZkKtVkMURXR1daGnpwfRaBQdHR2or6/vPb7L5cLUqVORnZ190b3qP6b+999oNEKr1fbOIUVRIEkS/H5/73wH0HsvLRYLVCrVkHGSLMu99zUSiQy4rzqdDkaj8aLn5vf7B8w7vV4/4Hn3fw6x+xd7LwiCALvdjuzs7IsEdmxuq1QqaDSai+a2Xq+HVqsdck7FCAaD8Pl84DgORqMROp0OkiTB5/MhHA73vicFQYBKpYLVaoUgCDdkLDmhBVT/faAkjFPldAnsOjsWpi7E3OS5kGQJnaFOHGg4gM8bPsf+uv34sPxDbCzfiF/t+xVSLCmYGj8Vc5LnYHbSbExLmAY1rwaHG2/SMxgMBmNwqqursXbtWmzbtg2VlZUIBAJw+0W6YgAAIABJREFUu92YN28eHn30URQVFUGn0wGggPC3v/0tNmzYgJtvvhnJycn4wx/+gPLycsTFxeGRRx7B3XffDUmSsHbtWrz55pvo6OhAVlYWHn/8caxYsQJ2u33A+SsrK7Fhwwa8++67qKyshFqtRmFhIR566CEsW7YM8fHxva994YUXsGfPHixfvhzf/va3Bxznt7/9LXbt2oWSkhL84Ac/AAD88Y9/xDvvvIOioiIUFBQMGOttt92GBx54ALNmzUJrayt++ctf4k9/+hOam5tx9uxZvPDCC1CpVPB4PHjvvfeQnp4+5D08d+4c3n//faxduxZnz56FWq1Gfn4+HnzwQdx+++1ISEhAKBTC888/j7Vr16K6uhoAsHPnThgMBjz44IN46qmnkJmZOejxm5ubsW3bNqxbtw5lZWVob2+H0+lEcXExVq9ejdtuu21A8N7Z2YnNmzfjr3/9K44fP47u7m5YrVZkZWXh4Ycfxr333gufz4df//rX+Oijj3q/fv/993vF3Ze+9CWsWbPmojFVVVXhtddew5YtW1BTU9N7rX/7t3+LkpKS3ufb0NCAF154AR999BGeeOIJ1NfX48MPP0Q0GsXdd9+N73//+/joo4/wxz/+EYWFhXjiiSfw61//Gq+++iq6u7vx4x//GM8++yw0Gg1yc3Px3nvv4YMPPsCrr76KuXPn4ic/+cmAOfzWW29h48aNqKysBM/zyM3NxTe+8Q0sWrQIbrcbAAmtxsZGvPTSS9i+fTtqa2shyzLi4uKQl5eHf/3Xf0VGRgbUavWgz6Gnpwe7du3Cq6++ikOHDqGnpwdGoxHp6elYtWoV/uZv/mbAz7a1teHtt9/GH/7wB5w+fRoulwt33nknHnjgARQV0T6ioVAIL774It577z3ccsstMJvNWLt2LZqamnDnnXfi6aefRkVFBV599VWI4v9n77yj4zjPe/3MzPa+2AIseiMqK9ibKBaRlGiJlBwVS7blWLLlONdx4nOuEyfnOFLsJDeRT3J8c31cpFix1SxLVqFE2RYlmkUixSYRLCgEQfSyKLtYANt3Z+4fK6wEkeqiSILz8ODwkJid/eabD9jvN+/7/t4UTzzxBACPPfYYTz/9NLNmzWLx4sX893//N21tbeTk5HDNNddwyy23sHz58vdcs1Ps2rWLH//4xxiNRr761a9y3XXXMTAwwE9+8hP27dtHb28vsizj9Xqpq6vj3nvvpaSk5D3naCYzowXUO8WBMgMFlCiIGWc/KbNwjVoja0vXsih/EbfPvp3B8CCto62cGjpFy0gLRweOsr93P1adFbvBzvLC5VS5qpjtnU1VThU5JtUqXUVFReVKZmhoCEEQWLZsGZs3b0aSJILBIHv27OFHP/oRd95557SaiXg8zsjICM888wxz585l3bp1XHvttezevZtHH32U06dP4/F46O7u5gtf+AKxWIyXX36ZRx55BEVR+NKXvpQ9V0tLCz/96U/Zv38/xcXFbN26lUQiwZ/+9Cf+67/+i56eHu655x5ycjKfVbFYLPtk/N3E4/FsZOHdY925cyexWIyvf/3rOBwO3nzzTV555RVkWcZut1NcXMytt96aFR4rVqxg27ZtmUwQoxG32/2e83f69GkefPBB/vSnP1FQUMD1119PMplk7969/PznP6e7u5tvfetb2O12br31VgoKCnj44YcRRZHbb7+dgoICiouLs5v88zE2NkY0GmXWrFksX74cvV7P+Pg4R48e5Ze//CW9vb18+9vfzh7/5JNP8vzzz6PVarnnnnuwWq2Ew2G6u7sBspHGWCzG4OAgTz75JOvXr+cf/uEf0Gq1vPHGGzzzzDMoisLNN99MTU0N8Xicjo4O/u7v/o6hoSFqamq44YYbiMViHDp0iH/8x3/kO9/5Dhs3bsTlcqEoCpFIhIGBAR5++GFWrVrFt7/9bVwuFzk5ORgMBpLJZDaS4vF4uOWWWxgdHeVPf/oT119/PevXr0cURaxWK0ajkUQikY3WQCZ62d3dzT/+4z9y9uxZKioquPbaa5Flmddff51///d/JxgMsnXrVrxeL6Ojo3z/+9/n7NmzLFiwgFtuuSW73tvb2z+wFu2ll17ikUceIRqN8rWvfQ2r1Uo0GqW/vx9RFEmlUllhEY/H2b59O3PmzGHVqlVs2rSJY8eO8fzzzyNJEhaLhfLy8uy69vv9PPvss6xcuZKvf/3ruN1ubDYbLpeL1tbWbIRpikQiwcjICN3d3SQSCe666y6cTieNjY3s2rWLdDqN0+mkpqbmvNcyPj7O9u3b+cUvfkFJSQlbt25l5cqVDA0N8fd///d0dXWxaNEibr311uwcnT179oqt14MZLqAU4W3RJJAxkNDrZ27ERSNqcBqdOI1OFJtCtVxNvaeeVUWrGJgcwB/20zXWxanhU/SGennl7Cvs6dyDy+TCY/KQZ8mj3ltPubOccmc5bpM7m+qnoqKiojLzKSkpwWQyIUkSVqsVSZKYnJzE6/Xy6KOPcvToUZYvX54VMZDZvOXn57NmzRqWLVuGwWCgpqaGH/zgB+zatYtrrrmGL3zhC1RVVSHLMpIk8eKLL3L06FFuuummbLTkj3/8I4cOHaKsrIx77rmHiooKUqkUFRUVPPjgg+zevZs5c+bwuc997mNfXzKZxOfzcdVVV3H11VdjtVqpqqqitbWVtrY2GhsbqayspKamhvLycmw2G1VVVWzatAkgK6Lei1deeYUDBw5QUFDAX/7lXzJr1ixSqRSzZs3ioYceYu/evcyfP5+tW7dSU1NDNBrlpZdeQhAEVq9eTUVFRTYN673Izc1l1apVLFq0CIfDgU6nIxqNUlFRwdNPP83evXu59dZb8Xq9KIrC8ePHmZyc5KabbuKGG27AaDQSi8UYGRnB4XCg1+uJRqPZe1lWVsbq1atZuXIlWq2W6upq2traeO2116ioqKCqqopAIMAjjzxCU1MTN998M5s3b6awsJBEIkFDQwP33nsvu3btori4mJUrV2bHHo/HmTVrFuvWraOhoQGTyYSiKOdEMEwmE9XV1ZSXl3Po0CHq6+uz92Aqxe7dRCIRHn/8cRobG1m/fj3btm2juLgYWZZZtGgRP/zhD9m7dy/l5eWsXbuWiYkJdu7cyYYNG9iyZQuzZ89GFEUmJyfx+/34fL73TNVMp9OcPn2a/v5+tm3bxp/92Z9lRV0gEECn02UjtVPzWlBQwOrVq1m+fDlGo5EVK1Zw3333ceLECU6dOpUVUFPrtKioiDVr1rB69WpsNhvpdPqctMB3kkwm8Xq9XHXVVaxbtw6bzUZ1dTXt7e20t7fzxhtvnFdA9fb28sILL/Doo49SVVXF1q1bsz/jra2tvPTSS2zZsoUtW7ZQV1c3bY5yc3PfN511JjOjr1oRFBRBQURAo4gkkxknvishVVMQBLSSFp/Vh8/qYx7zSMtpRiIjNI800zveS3ugnZ7xHgYnB2kabuJg30Fe63mNYnsxpY5SCm2F5Fny8Jg8FNgK8Jq9GDVGJFH64AGoqHyKDIWHiKViWHVWnEbnB79ARUXlY5Gbm0ssFstuuKLRKMlkEr/fz9DQED09Pfj9/mkCSlEU5s6dy+bNm8nPz0dRFHJzc3nooYdoamrC5/OxcePG7EZr1apV7N+/n8HBQYLBICaTiXQ6zYEDB5BlOWv3PFU/4/V6OXr0KHv27OHQoUOfSEAJgkBdXR3r1q3LRnmqq6uZNWsWBw4coKOjI1s3MlUvYzAYsnVU78VUPc2hQ4eIxWKsXLmSdevWZettcnNzOXHiBC+++CL79+9n27Zt2bqrqboys9n8ge8D4HQ6SaVStLW10dTUlK3BCQaDDA8PE4lE6OrqwuPxZF+TSqWy9TdWq5XCwsLzpiHKsszy5ctZunRp9h7X1NSwdu1aHnjgAU6fPk04HCYYDPLMM89k7+3y5cvRaDQoikJJSQnPP/88LS0tnD17dpqAUhSFNWvWTDv/+Zia96l7YDQa33dupurxnnvuORwOB+vXr2fVqlXZMZWXl2ftxFtaWrJueFORt8nJSZLJJB6Ph4KCAqqrqz/wPsDbdU0TExOYTCby8vKmuQUmEons+8ybNy8rNBVFoaysjLq6Opqbm+np6TnnehoaGlizZg15eXkfaiyCIFBVVcWGDRuyqa5VVVVUVVXR399Pe3v7Oe/R3t7Os88+y44dOygsLOT2229n4cKFOByOaZGlTzJHM5UrRECJaJFIpRREUUAUrwAFdR4kUSLXkkuu5e0c8sHJQdoD7ZwaPsUJ/wnaAm00DzdzqO8QkijhNDgpsmfqp2a5ZlFgLcCut2PVZ9IA7Xo7AsIVWUCocuGRZZnxxDgvnXmJgckB5ufNZ03pGjUyqqJygejo6GD79u0cPXqU0dFREokEqVSKZDLJyMgIExMTjI2NTXuNVqvF5/NlN3rvFAPFxcUUFhZOe0rtcrkwm83E43HGx8fJz88nFosxMDCAy+WirKxsmgmCzWajpKQEnU6XTTv7uOh0Olwu1zkpcjZbpvXHxMTExz53PB5ncHAQh8NBRUXFNMOLqbkwGo3ZmqePy+DgIHv27GHnzp0MDg6SSCRIJpOkUil6e3vJyclheHgYRVHQaDTMnz+fzs5Odu3aRSgUorKykrKyMgoKCvD5fDgcjuy5NRoNhYWFuFyuae9ZXV2NVqtldHQ0uw7a2tooKSmhvb19miNcKpVCkiQGBwcJBALTzqPT6SgsLDyn9u2TMiVk2traWLRoET09Pezdu/ecY0ZGRhgeHs6mAl577bU0Nzfz7LPP0tbWlu035fP58Pl87xkJlCSJmpoaioqK2LdvH7FYLDuvRUVF5OXlTUv11Gq1FBQUZM0fpvZMbrcbQRCYnJycdn6tVkteXt77pnK+G51OR05OzrQ6QcisPVEUz1nbqVSKAwcO0NzcDMA///M/U1tbm42wiqKIzWbjuuuuo7W1lWeeeYbTp09TXl5OaWlpdo6uxPonmOECCiHzJQoCkiKRTl85EagPS54ljzxLHiuLV2YcdZQUezv30jTcxNGBozQONrK3ay8vt79MUk5SmVNJubOcGndN1ozCqDGiFbVoJS1aUYtG1KhRKpVPjKIoxNNx9nfv50cHfkTTcBNfmf8V5njnkGf9cE/kVFRUPhqPPPIIzz77LDU1Ndx9991UVlZiNBoJBAL87d/+Lel0+hz75CmHr3c76k25vL075U2r1SJJUnbTD2Qd5aYcw97NlAPcVL3LO1HOY687Zfv8bnQ63Xk3fFNi5511JR+VqWvQ6/WYTKZzvm80GtFqtdl0uY/Lrl27eOihhwiHw3zjG9+gvr4eq9XK5OQkDz30EK+++irJZDJ7/M0330xubi5PPfUU27dvZ3h4GKvVylVXXcXtt98+rTeRXq9Ho9Gccy/fOfZQKJR19Nu7dy9Hjx49x51PluVsuuYUgiBgtVrR6XSf+kPXdDqddas7cOAAjY2N54ifdDqNoijZMbndbn74wx/yq1/9ildeeYXXXnuNeDyOz+fj+uuv5+677yY/P3/aNbyTjRs34nA4eOKJJ3jppZd47LHH0Ov1LFmyhFtuuYUbbrghe51TTnvn+xmZGts7mXIMfPfx74dOpzuv4HuvtT0VWVYUhYULF5Kfn5+N2E2N2+v18q//+q889NBD7Nq1i1dffZV4PJ6t77v77rvJy8t7zzmaycxsAfUOBECWQRRRBdT7oBE0rC5ZzYqiFdwp30kynWQkOsJrXa9xavgUJ4dOcqT/CH848we0khadpKPSWUllTiUNvgYW5C2g0lVJoa3wYl+KygxgLDbGD/b+gEJbIaFYiGA0yGB4UBVQKioXiD179lBRUcEdd9zBxo0bkSQp8zAjHv9Im7mPypRF+lSa2buZSh96Zw3IlBA6n1CKxWLnNZe4kExdQyQSOSeiABAOh0kkEu9bx/JhOH78OOl0mjvuuIPbbrstayPd1dV13noUu93O5s2bWbt2LZFIhPb2dl588UW2b99OMpnE6XRm0/mm5j+ZTE7bjI+OjhKLxTCbzbhcLhKJBBqNhi1btnDTTTed0+R2iqmeThcaSZIwm82Iosj69eu56aabqKqqOu+xPp8v+xqv18tf/dVf8Y1vfAO/388bb7zBjh07+NGPfoTH4+HGG2+koKDgvOcxm82sXr2aJUuWEI/HOXv2LDt37mT79u08+OCDeL3eD+V8d7EwGo1s3bqV0tJSHnjgAb773e9y3333UVJSkhVQGo0Gr9fLX//1X/PNb36TwcFBjh49yo4dO7j//vvxer1s27YtO6dXEjNbQAnv/CtjIiGKagTqvZj6gdFJOpDASKYXhFVvJceQw7qydUwkJphITNA/0U/LSAtnAmfon+jnQO8BXut5DYvOglVnxWf1UeuupcHXQLWrmnxbPg6D4wNGoHKloigKaSXN3q69lNhLqMipYDQyyq6OXXSMdXDH3DtIyamM8+Rn1BA6Laf57zf/G4PGwJKCJdS4z+9epKIyE5gSIZOTkxQUFGC327N9Y2RZ5uDBgwwPD0+rq/m0EAQBg8FAaWkpx48fp6WlhS1btmSfagcCAVpbW4nH49OaprpcLpLJJKFQKNsnBzL20gMDA+ekGn5UNBoN6XT6Q0el9Ho9paWlvP766zQ1NZFKpbKCJhgM0tbWRiQS+US1I1P9mYCse90Up0+fPqfOBcj28dLr9VgslmwNVFNTE8PDw/T29k6rhzp58iRnz56dZjiwf/9+IpEIubm5uN1uwuEw8+bNo7e3F4fDQX19/XmjEJ80vWuqJ9QH3YMpJ7t58+YxNDSE0Wh8zzFN3RNBEJAkKdvjymQy4XK5cLlcPPnkk5w9e5bx8fH3FFCiKGajPhaLBZPJhM/no6+vj8OHD9PZ2XlJCyhBECgsLOTzn/88Go2GBx54gPvvv5+vfe1rzJ07NyvM3z1Hbrcbp9PJ7373O9rb25mYmFAF1IxGyUSgBEGNQH0UBEFAJ+nwmD14zJkPTkVRCCfDNPgaGImMMBoZZTA8SN94Hz3jPfSGeuke6+bk0En2dO3BY/LgNXspshVRaC+k1l1LmaMMu8GetWBXubJJyklODp3k18d+zbaabZQ5yvCH/exs30mNq4YSewkmrQmDxoBV98FF1p8GCgr7uvbRFerizYE3uan2JlaXrP5M3ltF5WJRWlrKwMAALS0t1NfXI4oiJ0+e5Pe//z2Dg4PU1dV96u8pCJk62g0bNtDV1cVLL72Ex+Nh/vz5JBIJdu3axZEjRygtLeWqq67Kvm7OnDlYrVZOnDjBvn37WLBgAZOTk+zYsYNTp059onQ8yBg/aLVazpw5w8GDB7OOY1P/f75rWLNmDW1tbbzyyiv4fD4WLVpEMplk9+7d7N+/n8LCQtatW/eJx9XY2MixY8fYsGEDNpuN1tZWdu7cSVNT0zSzhVAoxK5duwiHw5SXl+NwOBAEgebmZkZGRvB4POfU6uzduxen08lVV12FwWCgqamJP/zhD5SVlTF79mz0ej1ut5uvfOUr/OxnP+O3v/0tgUCAqqoqjEYjkUiE/v5+UqkUs2fPfs9I0AchiiJ5eXmIokhzczNHjhzB4/Gg0+nOqQ0SBAGLxcKXvvQlfv7zn/Pcc88Ri8Wora3FZDIRjUYZGBggkUhkjRX6+vp4+umnqa2tJS8vD4PBQCgUorGxEVmWycvLO28qJmRE+uuvv05PTw9VVVXk5OQgCALt7e309fVhMpnOqUW6FDEYDFRWVnLjjTcSiUR45ZVX+NWvfsVtt93GvHnz6O/v5+mnn2b27NnZOQoEAhw/fhxFUfD5fO/rSjmTuWIElALIsvKWeFIV1CdBEAQsOgsWnYVyZ8Z2U0EhEAnQO95Ld6ibrlAX7cF2BicG8Yf9dI51sr9nP0atkVp3LaWOUopsReRZ88g151JgLcBtdiMJV2ZH6yudRCrBy2df5kzgDJFUhFg6RneomyMDR7h9zu0ICCTSiUw01PjZ9SuryKng5NBJTgydYH7efFVAqcxYpn7vXn/99Wzfvp19+/Zl7ZiHh4fJycn5xKlnH8Tq1avp7e1l9+7d/Pa3v+XgwYOkUinOnDmTrbmYM2dO9vja2lpWr17NgQMHePTRRzl06BCCIDAwMIBGo8FisXyi8dTV1VFfX093dzcPPPBAthfPPffcc47JwhQrVqygr6+PnTt38tRTT3H06FHS6TTt7e14PB62bNnC/PnzP/aYpnp09fX10dzczAMPPIDNZsum2OXk5Eyrf0omkzQ1NXH8+HFycnKydTUDAwM4nU7WrFnDrFmzsscbDAYcDgednZ309vaSSqXo6OjAYDBw7bXXMn/+/Ky5wA033EBnZyctLS08/fTTuN1udDodsiwTj8cpKSl5z9S+D4NGo2HevHnU19fT3NzML37xC1wuF7m5uXz9618/53ij0ch1111HT08Px44d45lnnuG1115Dr9cjy3LWSjw3NxdZlgmFQuzZs4cTJ05gsViyNV5DQ0Ns2rTpHLv+d5JMJmlra2PXrl0cOnQIg8GAKIoMDw8DsHbtWurr6z/2tX+WTImou+66i1gsxptvvokoiiQSCUwmE7t376apqSmbohqNRvH7/dk5+rQNQS4XpHvvvffeiz2IC8Uf9/2R44HjuHMMLGQOjR21+Hw6Fiyw4vWqLl6fJgICJq2JPEse1e5qFhcsZlPlJubnzafKXUWeJQ+tpCUUD3F27CwH+w5yuP8wx/3HOTt2lmA0yHh8nLHYGJOJSZJyEhERjfh2qF1lZiLLMoFYgP888J+UOEpYW7oWvaRnb9de9nTt4bsrv4s/7OeY/xiVOZVsqtz0ma0Hn9WHVtRS6ihlXt48ShwffzPwXkSSEcZiYyTSCbSS9jNLUVRROR+lpaWIokh/fz8nT56kv78fl8vFrbfeSjqdpqSkhAULFpCbm4uiKPT09GR7/9TW1k47V0tLCw6Hgzlz5kzrcROJROjr68Plck2zs3Y4HBQVFWG327NNQcPhMLW1tdx6661s2LBhmmOc0WjE4/EgCAJnzpyhpaWFyclJ1q5di8/nw+12U11dzbx584BMv5t4PM7s2bOZO3futLH29fWRSqWorKxk4cKFQCZFUKPRMD4+Tnd3N729vYyPj7Nhw4b3tNS22+1Zl7mpa5icnKSqqoqbb76ZTZs2TdtwTk5OMjAwgNfrZenSpdhstg+8R7m5udjtdkZHR2lsbOTMmTMYDAauueYaSkpKkCSJFStWUFxcjCRJTExMEAqFGBwcpK+vj0AggNvtZsuWLWzcuJHCwkLC4TD79++nvb2dL3/5y5SXl9PS0kJ/fz92u53Pf/7zXHfddRQXFwOZlDmbzZaNSAUCAXp7exkeHiaVSuHz+Vi8eDHV1dVYrdZsk16A9evXnzfly+/3Mz4+TmVlJUuXLkUUxez9DYVCdHd309fXRyKRYNOmTQQCASYmJqipqWHRokVZYVdbW4vZbCYYDNLb24vf7yeRSJCbm8vChQupq6vDbrejKErWVXJgYIChoSHS6TRVVVX8+Z//OQ0NDe8rwqPRKOPj4/j9fnp6eggEAthsNtavX8/1119PeXk5sizT29tLMpmkoaHhnD5MXV1dKIpCTU0Nc+fOJZ1O09fXRzKZZPHixeeN3o2OjjI2NobH42HDhg1AZv1ORdwWLFgw7fj+/v5sf68lS5YA5/4sSJKE0+mksrKSkZERRkdHsdvt1NbWEg6Hp82RLMtUV1dn5+hCP1i5VBGU81VfzhD+5l/+hofbH6a6ws7dyhd4ZNfNzJ9v5qtf9VFff2Xe8IuJoihEkhH2du+lcbCRg70HaRpuYiQ6QjwVR0CgzlPHbO9sGvLfMqTIqcw6/GlETcbhT41SXTak5XQmteV9rO6jySgnh05y3WPX8b1V3+PmupvpHOvkoWMP0TnWybO3Pcv/HPsfdnXsYn3Zer619Fuf8VVcGKZcBk8OnaRpuAmrzsrigsXkmnPRiBp1jauoqHxmDA0Ncf/99/P888/zb//2b2zduvViD0lF5ZJmRqfwCUpm45ZCIULyg1+gcsExaU2sK13HVcVX8Y1F3yCSjNA91s3Ojp00DzdzsPcgTzY9yZNNT6KX9DgMDubnzWeBbwFzvHOY7Z1Nsb0YSbjyLDMvR0aiIxgkA1a9FeE9UmdHIiO8fPZlTBoTDXkN5Fny2NO5h/ZAO9eUX4NW1NIZ7MSkNeE1f/ieGJc68XSc37f9nv/z6v+hK9SFJErM8c7h/mvup9ZTi0aY0b+eVVRUVFRULltm9Ce0IAsIskAamQRpRBEUJfOl8tkz9URdr9GjJ+PuZNPbcBgcFNgKCCfDBKNBBiYH6Ah20BZoozvUzaG+QxwZOIJZa8aqt+I1e6lwVDDbO5siexE17ppsiqDKhUFWZM4EztAd6mY8No5G0pBnyaPWU4tJazpH0CbTSfZ17+PBNx5kYGKAHGMOedY8cgw51Hpq2VC2Aa8lI4ZGIiPsPLuTFcUryLXkMhIZ4XTgNEk5ybqydQiCQFugjVxLLvnW/Itx+Z86qXQK/6SfHx/8McWOYr7a8FXGYmO8ePpF/vXVf+WnW36KTW9To1AqKioqKiqXIDNaQImyiKAIyMgkSSFJArJ8/p4RKhcHURAxaU2Y7G873YQTYQLRAMORYUYjo3SOdRKIBegN9dI73stwZJjeUC+vdr+K3Wgn15yL2+TGY/ZQai8l35pPoa0Qn9WHSWtSa0o+AbIiMxwe5ndNv+NA7wEmEhMZRxYBJEHCZ/VxbeW1LCtchsv0dlG1IAgUWAto8DXQYeggno4TToSZjE8ST8dZWrAUL14m4hOcDZ7lTOAMX5z7RdwmN03DTfSO95JvzWeWaxadwU4GJgdY4FvwkWqQZEUGmHb/o8koA5MDRJPRrHB/J5FkhI5gB92hbjZWbEQUxAsiYoKxIHu69tA11sUX536Rz1V9jkA0QCgW4rETj9Ey4AHyAAAgAElEQVQ51km1qxqD1vDBJ1NRUVH5hFgsFrZt28b8+fOnGXWoqKicnxktoARFQFAEFAVSShpJyjjxqfrp0sasM2PWmSmyv92AbzIxmbFHH++mJ9RDd6ib/ol+RiIjdAQ7OO4/joCAVW/FZ/FRZCuiwFaA1+zFY/aQa87FbrCTZ8nDoDGooupDMpmY5Lj/OA+88QDF9mKK7cXYDXZScoqh8BAnh04yMDGAXqNnWeEyIskIzcPNdI51Ek6GEQWRVSWryDHmkEglmExkmktadJnC3P6Jfk4MncCoMbKkYAk2vY2m4SaC0SDz8uZh1Bg50HsAAYESewkek4fx+Hg2GlZoK6TCWYHTmCnKVhQlaz+uk3SUOcrwmD1MJCY4OXSSU0OnaA+2E01GKbIXsbZ0LYsLFgMQT8U53HeY51qeYzgyzNLCpdj0tmmpdLIik0gn0Em67BpSFAVZkZEV+UPXLo1GRnm5/WXKneUs9C0k15yLTW9jUf4ifnbkZ/SEeihxlKgCSkVF5TPBZDKxcuVKVq5cebGHoqJyWTCjBRRK5ktGIYWMRiOSTitqBOoyxKKzUOOpocaTcbCRFZlYKkZ7oJ3m4WbOBM/QHmjnbPAsXaEuTg6fJJaMYdKayLflU+mspMBWwBzvHHKMOVj11qwVu0Vnwag1ZqINqsX9NILRIMcGj9ER7OD+a+5naeFSrHoraTnNaHSUl9pf4t7d97KrYxdmrRl/2M/jJx6nY6yDaDKKVW9lTckarq++noUlC9Fr9NlzK4pCx1gHJ/wnaPA1UGQrIq2kaR1tRVZkFvkWEU1FefnsyxTYCvBZfAyHhzk6cJQ/tv+RAz0HuKb8Gr48/8tZAZWSU/jDfn525GfUuGu4btZ1RFIRDvcf5oXWF2gLtCEgEEvHkHol/JN+FuUvQkGheaSZR088yhMnn8Bn9TEaGc0KPYBYKoZ/0k/zSDOri1dj1BoZjY7SP95PIBograSz6+v90kllJeM6+MbAG3y+7vO4jK5Ms0JRQifpUFBIKSn195SKioqKisolyowWUFMpfCklTVxIotUKpFIKsnyxR6bySZlK/ZuTO4c5uW+nGyTTSfon+znaf5SmoaZM1GHkFEf7j5KSU6TkFFadlfKccubmzmWOdw713nqqXFWYtCa0ohZJkLKOf3BlW6in5BSxdAyjzkipsxSzLuNeKYkSXrOXz9d+nj2dezjcd5hANMBkYpLWkVa+MOcLuE1u9vfs55mWZ+gd7+W+tfdl+4ZBxkRhSvD+ryX/C52k40zgDF1jXbhMLub55hGIBtjTuYc759+JKIj88tgv+eWbvyQUCzGRmKDUUcpEfCJ7znAizNPNT3N86DhrStYgCAIPNz7MTw7/hBJ7Cd9c/E3Wla+jM9jJ4ycfp3mkGcgIxZ8d+RmvnH0lG0UyaAzTBHX/RD9PnHyC/3vo/7LvK/vIMebw+7bf8/DxhznYexBJkPjxtT/m2sprs02nz0csFWM4PEzvRC8L8hZg1WfskEfCI7QH2tFLegpsBdPEpoqKioqKisqlw4wWUIKcSeFLIRMlgdEokkyqAmomoxE1FFgL8FZ6uab8GpJyklgyxnB0mFNDpzjSf4QzgTO0jrby+InH+Y3wG7SiFqveyqycWcz2zqbOU0edp46lhUsRubJT/RwGB2WOMoLRIGcCZ/Cavdj0b/cpkQSJlUUrOdh3kDcH3mRL1Rb+ad0/satjFz878jOWFy2nzFlGIBpgd+fuaQKqPdBO03ATJq2JDeUb0Ek6DvcfJpFOUO4sR0Bg59mdxOU4JY4SHjnxCIf7DlPnrqPUWcoTJ5/gzvl3Mts7O3vOaCrKrrO7mJc7D4vewm9P/pYdbTu4sfZGvn/V93EYHOg1elqGW4in4tmmvP9x4D842HeQlcUrMWlN7Ovah81gm5bq2TLSwotnXuS6yuvon+jnvj33cbj/MFWuKr6z/DvsbN/JgZ4DLM5f/L4CKhgNZlz3BIlaT21WlB73H+eP7X+kKqeKckc5Rs2V2d1dRUVFRUXlUmdmCyhFQCdLiHKacSmKwSAQjcqk02pqzExFEAQ0wtvRIwDZIOMyuSi0FrK0YCmRZISJxASjkVF6J3ppGW6hY6yD/ol+Xjj9AjtO78Cis5BjzKHWXUutp5Y6Tx2zXLPwWX1XVJqfTW+j2lVNqaOUF1pfoNhWTJ23Lvt9SZRYW7aWZ1ufpWusi8HJQdpG23jh9AtsrNzIyqKV2bqj0cjotHOfGDrBUHiIublz8Zq9iILI4b7DmLVmqnKqGI2MsrtzNwt9C3ny1JMk5AQ3199MnbuOx08+zqqSVVS7q7NpdgqZvkqN/kY2VWzimeZnGImMsL58PX+55C/Js+RlTSEGJwcZiYwwyzWL35z8DTvadmTrod4YeANJlDBrzVkBFYqF6Ah20BPqYWnBUr7/p++TkBPcNvs2Pjfrc8TSMfZ37yclp7LmFe/FRGKC4cgwbpMbu8EOwPOtz/Orxl8Riof4zrLvYNFZrujIp4qKioqKyqXMjBZQACZZg0ZOEJAmKTZLBIMpUilVQF1JiIKYsU7X6Kc5xcVTcULxEINFmc30UHiIwYlB+ib76BrroifUw77ufbze9zpuk5tccy4FtgLqvfX4LD6qXFW4TW50ku4iXt2FRStpKbQVctvs29jeup3FBYvxWry4TW4gM7f51ny+1vA1Vpespn+8n9d7X6fUUcrtc26nxF5CW6CNeCqeFQuQcbs74T/BeHychb6F7OncQ+dYJwd6D4ACz51+Dm2bloO9BzHrzAyFhyiwFmDVWREFkfZgO3+z7G/INeciiRkL9WQ6STAaZDgyzJuDbxJLxVhRtIIvz/syVa5MN3cBISOGxjoYmBygxFHC/zv0/6hyVXHtrGtxGV00DjbyVuvf7HgHJwfpHOtkODLMvq59GDVGbqm/hc2Vm6nMqaR5uJlgLMh8w/wPXA+TiUmC0SA5phxaRlo47j/Oy2dfJplOcnPdzawpXaNa8quoqKioqFzCzHgBZVG0kBYY1UxQb5WIRmWSSVVAqWT6UXk13mnNWaPJKEORITqDnXSOdWYsrce78Yf9NA03cbj/MPt79uMxeahx11BgLcj2J/KaveRb8z+0E9vlgtPg5M9q/4xXu1/l5bMvY9PbuLr0apxGJ4IgoJW0bKzYyOKCxTx+8nH2dO7hqw1fZaFvIf0T/fSEetCImmmpdlN9vrrGumgcbKTR30jnWCf9E/34LD4C0QAiIuXOcg73H8Zr9uKz+rDoLLhMLq6bdR3rytZNSyeMp+IMhYdIpBOcGj7F5srN3Fh7Iw2+hmliaMo2vWe8B+eIE0mU+MLsL9DgayCWjGHVW4mlYpwcOpm1Eh+YGKAr1IWsyCTlJHfNuYvPVX8u25cqkU4wMDmAx+zBoDm/c14oFmI0OsoJ/wlOj54mGA3ycOPDjEZHseltXFVyFVtmbcmKUxUVFRUVFZVLk5kvoGQtqbTICJNYLBLxuEwyKSPLCqI4cza5Kp8ORq2REnsJJfYS1rAGyFhOnw2epWm4iUZ/IyeHTnJ69DSH+w8jKzK55lxqPZlUv4V5C/GYPdgNdmx6G1ad9bKKJiiKwkRigkgigiiKmLVmjFoj1e5qvjT3S/zPsf/hd82/QyNqWFW8Kut+p5W0xJIxRsIjKCisL1vPZHyS51qeo2+8j0X5i5jjfdvs40DPgYy4Gu8hFAsxN28uI+ERcs25bKrclHH701mZiE/w7T98m3pPPWtK1rC0cCnzcudxdenV5wjVeDrOaDSTJugwOLih6gaWFy4/x7K+K5RJNQwnwoSTYb678rtZMRZJRKjMqcRtcrOnaw/F9mIMWgOBWICx2BhljjLuariLW2ffOi2ipigK8VQ8OwaNqMnW30VTUcLJMN1j3XSEOjjSd4RTQ6dIK2nOBM6wqXITW2Ztoc5Td1mtFRUVFRUVlSuVGS+grLKWeEriDJOYrW9tdN4SUXq9dLGHp3IZ4DK5cJlcLC5YjIJCWk7TPNzM/p79HOw7SONgI8+2PMuTTU8iyzIN+Q0szl/MssJlLM5fjNvkRiu97e53oZqzfhooKBz3H+fYwDF0Gh217lqqXFUYNUZuqr2JYCzIrxt/zf377ycpJ9lWsy2T7CYIDEeHGY2OYtVbcZvc7Di9g0ePP0qDr4FtNduw6q3Znkn7e/cTioUoshcxP3c+/7HpP7jj6Tsod5ZzY82NLC9aDoB/0k+RrQhREKn11FLhrCCWiiEIAvF0HKPGmJ3PtJwmmowiILClagvzfPOyDnfvxKa34Ta6afA18M3F32Rbzbbs90w6EyuKViArMhPxiWzkSiSTqjjHO4dvLv7mOec0ao1U5FTwcvvLxFNxnEYnI5ERukPdnA2e5fToaVLpFCadCZRM9HNz5Wb+Zf2/4DA4zrseFDItF9JyGlmRSSvpbL8pWZHRS/qMU+AlupZUVFRUVFRmKjNeQJkUDTpFC4KCxhgHASIRmXhcQa+6BKt8DCRBotpdTZmzjJvrb2YyMUnfRB9H+o5wqO8QxwaP8diJx3j4+MOYtCa8Ji9ry9ZS76lnRfEKKp2VSMKlK96HI8Ps7tzN0YGjRFNRnEYnde46iuxF+Cw+6jx1HOo7xH8d/C9WF68mx5iDJEhoBS2iINI01MRtT93Gcf9xNlZu5Evzv8T8vPkApJU0HcEOWkdaWZi/EAGBNwbe4PnW52kcbGRz5WZ8Vl92LDa9je+v+T4/2PsDvvniN8m35FNsL8aizxhHfG/V96hwViAJEgaNgXxbPnmWPLZWb6XMUXbe61tRtIJ6Tz0pOZWNoL2TfGs+W6u3oqBg0poA2Fi5kdWlq9/zvhXbi/mX9f/Cfx74T55ueRpREMkx5FBoL+Tq0qu5q+Eual215Fny+GP7H3nk+CPUeGo+sF5qcHKQ9kA7ZwJn6BzrpHe8l86xTobCQ9xSfwv/e+X/fs+UQRUVFRUVFZULw4wXUHpFQqtoQJTRmOIIokwkkiYeV73MVT46AgIIoJN02c2vQ+/AbXJTai9lffl6grEgPaEeWkZaaBpqoi3Qxu+afscOzQ6cbzgpshVR7a7O2qVXOCsw6UyXhLufgMCKwhWU2EvwT/rpCfVwNniW8cQ4nWOdHBs8xsDEALFU7Jx6n1JHKZsrNxNNRpEEiS1VW1hRtIJqV/W0nkaSKNHga2B50XKiySgnhk7w4BsPkpAT1Lhr8JrerknTS3qWFy3nRxt/xHH/cTqCHQRjQVJyCrfJjUEyZFP0zDozS/KX8MhNj1DvrcesNZ/3Gg0aAzpz5t69O70PMlb4Gt30X41GrRGj1vie98ikNbEofxH/tPafmExMApk1YtQaMWvNWPQWrDorekmPSWsipaRwGTINdAVByPQvm+ineaSZ7lA3LSMZZ8hAJEAkFUEURLxmLzmGHOo8dawtW8tVxVehFdWUPxUVFRUVlc+aGS+gJARERUQUZUxWGVGEyck00agqoFQ+HURRxCSaMGlN+Kw+FBQmvZMszl9M30QffeN99I730hXqoi3Qlv3a1bELn9VHniWPWTmzKHeUU+IoodxZjlFrPO/m/kIjCAK5llxyLbkk00lCsRD+sJ9gLMhweJix2BjRVBStpKXEXjJtnFa9lSUFS3Cb3KTlNKXOUtxG9zTxJAoibpObO+beQb41n9bRVtxGN6/1vEZ5Tjn51nwM2rdFmSiKOAwOlhUuo8JZgT/sZyw2RjKdxKq3kmPKyaawaUQNLpOL1SWrP/A6P+rcfpC4lUQJm97GAt+C9z1OQSGRTjARnyAQDfB86/MMTg4yMDlA/0Q/oVgoO6c2vY1SeylukzubRurQO7Ab7OQYc/CYPFkHQhUVFRUVFZXPjhkvoJS3/kgS2B0iopQRULGYKqBULgwCAla9FaveSkVORabuLh2na6yLlpEW2oPt9I33MRQZon+in6ahJl7veZ08Sx4ljhKqXFXkmfMosBfgMXnwmDKmFJ+1oNJKWtxmN27zh3OFEwQBr3m6q+G7mRIGywqXAdA73ovT6CStpFmUvwiHwXHe6xQFMSvsLjcURSGtpOkc66RrrIsjA0cYDg+zq3NX1igjKScxao0U24spcZRQaCuk0FZIgTWzBqZSFlVUVFRUVFQuPjNeQKVRSAsKkiTgdumQxCThsKxGoFQ+MwRBwKAxUO2uptpdDUBaThNOhjncf5jDfYdpHGykaywTodreuh2rzkq9t55qdzW17lrKHeVY9VbsBjsmrQmLzjIj+k9JgoRO0qEVtSzJX4JNZ/vgF10GKIpCLBUjGA0SjAUzTYG7dnO0/yjHh44TSUXoGutidfFqFucvzq6NQlvhtCbQKioqKioqKpceM/6TOinIJIUUGklLbo4FjSZKOJwmFktf7KGpXMFMpXytL1vP+rL1yIqMf9JPo7+Rg70H2d+7n1e7X2VH2w7Schqz1kytp5Z1Zeuocdew0LeQAltBpl5H1GTNDS43R7YpVz6dpGOhb+F5XfMuFxQl018uJaeIp+O0jrTy+7bfs7d7L0f7jyIrMrO9s/GYPNj0Nn6y5Scsyl80I4SwioqKiorKlcSMF1Bx0sRIIYl6vHYnVssY8XjGhU9F5VJBIJP+tqZkDcsKl/GN1DcYi43RNNzEkf4jHOw9yJGBI5wcOolW1GLQGKjIqWBV8So2V2xmUcEi9NLlZyuZkBOklBT5toy73jvrpS5HxuPjvNLxCs80P8PBvoMk00kW5S/ivrX3saxwGRadhcdOPMYLp1/AolPT8lRUVFRUVC5HZryAiohp4lIas2hAr9Fjs2qIxxU1AqVySSEIApIgYRQzbm+Q6T/lNXuZlzePG2tvZCg8ROdYJ22jbTSPNNM51skjjY/wUvtLOAwOalw1lOeUU+WqotZdS4mjJNuj6VIlmoySSCeoddWi1+gvinHGJ0VWZMZiY+zt3MtTzU/RHerGaXBy2+zbWOhbSIm9BK/FS44xh0gygl6jRxAENILmkr43KioqKioqKudnxguomJAiJSnYxIzdsdWqwe9PqCYSKpc8GlGD0+jEaXRS7iwnLacZjY7in/TTP9FP33gfPeM9GXOCUBdvDr7Jof5D2PQ2fBYf+dZMVKfcWU6uJZcCWwFuk/uSsEufIhQLEYgEWJS/6JLujfVexNNxTg2d4rmW5zjUdwitqOXq0qtZkLeAOk8dJfaSaa6Ck4lJFEVBQEAUxUvqXqioqKioqKh8OGa8gIoLaRQBcoTMJsZq1dDTEycWU1P4VC4vJFHKutzNyZ2DoiiMx8dpD7ZzNniWzrFOOsc66Z/op2W0hb1dezHrzFQ4K8i35VPuKKfMWYbH5CHHmEO+NR+b3oZWuji9hFJyikAswGh0FK/Ze9lFnyLJCIf7D/NM8zMc6DlAtauazbM2s6ZkDXmWvPNajE/VfAGXpWBUUVFRUVG5XEmlFCYn00QiaYxGEYfj42eCzHgBlRBkBFHBLGYKtS0WkWRSJpGQURRQM2hULlcEQcBusNPga6DB1wBkREl3qJtDfYfY17WP4/7jdI51cmr4FKl0CrPOTJG9iFk5s1hauJRCWyFOoxOrzopFZ8GgMWDSmpAE6YKnl4UTYQLRAIl0Ap/VhyheXgKqdbSVXx/7NYf6DrG+bD3fXfVdvGbv+7royYqMrMiZlE21h5OKioqKisoFIZ1WSCQyrtvRqEwyKZNMKoyOpohG0xQW6rHbNR9bB1wBAiqNJChYhExxutkskUpBLCZnUmlUBaUyg9CIGsqd5ZQ7y7lt9m0AtIy0cNJ/kkZ/I4f6DvF67+vs7drLL974BQCljlKWFS5jSf4SypxlzPHOwWFwoJW0iIKYraP6tJ3+RiOjjEZGMWgMFNuLL5sIlKJkesv95sRvOB04zS31t/C91d/7UPbjsiIjyzIiIhpRo6bwqaioqKiofEIURUGWQVFAlhUUBcLhNAMDCZqbw5w5E2NwMI5eL1JWZmDBAgt5ebpPFESZ8QIqiQICGMhEoMxmCVGEREIhkVAwGNQNjMrMptxZTpGtiPXl64mlYozHx+kKddHob+TU0ClaRlp45ewr7Di9A42oQSfpqHBWUO+tZ1bOLPKseeRb8pntnY1Nb/vUUs9C8RCheAiT1kSFs+KySmkbCY9wYugEVa4qrqu67kOPPa2kSZMxsFH7PamoqKioqHxywmGZrq4YAwNx2tqijIwkEUXIzdVRUWFk5Uo7Go2AJAloNAI6nYhO98n2/zP+EzwppBEFMAqZOg+jUUSSBFIphWRSxmC4PJ56q6h8XHSSDp2kw4wZBQWv2Uu+NZ9ady3jleOE4iFGIiN0jXVxavgUw+FhgrEg+7r3sbN9J3qNHqPGiN1gJ8eQQ64ll1xLLnmWPIrtxVQ4K/BZfNPMEj4MToOTublzsevtuE3uyycChUIsHSOaimLQGLDr7R86KpeSU6TSKURBVPs/qaioqKiofETSaYVgMEl3d5zu7hiDgxljOLtdg92uYdEiKwaDiEYjYDRmzOMcDg2i+On2ypzxAiolyGgEBcNbAkqvnxJQmTooFZUrCYFM7Y1Vb53WtDaRThCMBumb6Ms440UDDIWH6J/oxx/2E4qHmIhPMDg5SM94D0k5iYCAy+Qi15xLsb2Yq0uvZlH+og/dDNdj9rChfAMT8YnLqv+TQKb2LNecS/94P6eGTlGZU/mhXptMJ0nKSURRxKAxqCnEKioqKioq5+Gt3vSEQin8/gR+f4JQKEUsJr+1lweTSaS0NPNZ6nRmBFRBgQ6TSUIUL+zn64wXUGkUZAF0QuZSdToBUcw4caRSqhOfigpkolRTkaUpZEVmPD5O/0Q/gWiAUCyEf9KPP+LP/D3pZzw+TvNIM0cHjqKTdJQ7yz+0gDLrzNR56i7UJV0wBEHArrezqngVL5x+gZfaX6LeU0+l64NFVDKdJJlOohE1mX5Qag2UioqKiooKigKxWJrx8TShUIpQKJPuHo1m/h0Op0kkMnt3o1HC59NRVKTH6dSg0Xz2GSwzXkDJAiCA5q30IK1WRBQF0ulMGFBFReX8iIKIw+DAYXCc872UnCKcCNMT6qF5pJmDfQdxm9wk5eRFGOnF4fqq6+kd7+Vg70F+c+o33LXgLjxmz/vWNsXlOCk5hU7SoRUvjn28ioqKiorKxURRIJWSicVk4nGFWCxNKgXj4ylGRpIMDsbx+5MIAjidWgoL9dTXm/H5dBiNl0a99IwWUIqgoAgKIgIaMgJKowFRzIinVOoiD1BF5TJFI2qwG+zYDXZm587m5vqbL/aQPnNKHCV8cc4XiaViPPjGg8iKzF8s+gtcJlfWufDdxFNxZEXGqDFehBGrqKioqKh8tmRS8TLOeO90yRsdTdLWFqGzM05LS4TJyTRer46qKgNz51qorTV/6nVLnyYzW0CJGQElIWIiU2Mx1WomcxMv4uBUVFQue2a5ZnHnvDvRSTp+evin+MN+vrXkW1S7qs97fCKdQEbGoPlohhsqKioqKiqXK/G4Ql9fnKamMB0dMUZHk5jNEmVlBsrLDaxb50CnE99yyBPeyha72KN+f2a0gEpr0qSlNDrBgF3MbFhEMfNkOKOE1RQ+FRWVj49eo6fKVcXts2/HoDHwbMuzRJIR7px3JyuLVqKVpqfpRZNR0uk0Fq3lIo1YRUVFRUXlwqAoCum0Qn9/gs7OGL29ccbH00iSgN0u4XRqWLHChlabsRG32TSYTBmnPEm6dKNN52NGC6iUNoUsyRgELTmiGZgSUGRDiSoqKiqfBLPOTI2nhi/qvohZZ2Z3524eOPoAnWOdrC9bT5G9KHvsZGKSpJzEbXJfxBGrqKioXJ4oikIqlaKvr4/h4WGCwSCRSIREIkEymanBNZvN5OXlUVJSgtfrRZLOrZl55wP0y2nTfimhKG+n4o2MJBkeThIIJNFoMvMpSQIulxaXS4tGk3HJ83i0uN1a9HrxgrvkXWhmtIBKa9LIGhm9oMElfjhnMBUVFZWPikFjoDKnkr9Y9BfYdDZ+3/Z7nmp6iqHJIdaVr6PeU49eo2csPkYyncRlcl3sIV/SyLJMMpkkGo1is9kQL/VcDhUVlQuKoiiMjY3R0dFBa2srzc3NBINBotEoiUSCdDqN/FZdhiRJWK1WSktLqaysJDc3F7PZjE6nI51OEw6HGRsbQxAErrnmmvMKrPMx9Vqz2Ywoilec8JJlhUgkzdhYxiEvGMyYPMTjCpGITDicJhqV0esFPB4txcUGfD4dFouGmThVM19AiVMCKhOBmipeEwRm5A1VUVG5OIiCiE1v4+6Gu6nMqeTRE4/y6IlHOTV8ijvn30m5o5zusW7i6TgF1oKLPdxLmlAoRHt7O729vWzcuBGj0XjFbVZUVFTeZmJigsOHD/PUU0/x+uuvI8syPp+P/Px8HA4HRqMRozFjzjM4OEhrayv79u3DZDJRWVmJy+XCZDKRSqUYHR3F7/fjcDhYt27dhxZQsViMEydOUF9fj9Vq/dCvuxyR5YxdeCyWccqbav0TCCTp6YkzMJCguzuORgMVFUbKygzMm2emsNBwxeytZ7aA0qaRNWkMghaX9P/bu9fYuM77zuPfc86cuXLIGd7Em0hRokTqfrMty7ZcW5W1Xjdp6thu4nYbYxt0s1ig+6LbTZEskAJ9F8DtmwRbNE1aNF0DixaI68Z2ZBu+RIm9tiTbkijqQpkUJZoSbyJFcjjXc9kXY1Jy5Itskxpy9PsABxyOODP/4ZDi/M7zPP+nGKBc18f3fUyTZT98KCJLj23ZPLDmAbpqu3j69NP81Wt/xTNnnuGxDY9xcuwkVaEq1iTXlLrMJe3NN9/k+9//Pr29vbzxxhu0tLQQCJT1nysR+QTvvvsuP/7xjzl06BDf+ta3+NrXvkZzczOh0NVN2Oem5bmuSzqdpqenh9dff52TJ0/S09PD5OQkwWCQ9vZ2HnroIb70pS9h2ze+ncSVK1d46qmn+JM/+RM6OzuJRvho3vgAAB2WSURBVKML/jxLYe77Nre0xfchn/cYHy9w5kya06czDA/nKBR8mpqCrF8fY9++JO3txcB6qwSm31TWf5HcgAsWRLCp+KALn+syPwKlWSEislgaKhr4g81/wK7mXfzz8X/m8NBh8m6eBzseZHvj9lKXt6Tt3LmTb3/72xw5coSamhpN4RO5xTU2NtLcXBy5n5ycpKam5rrw4zgOFy9e5G/+5m+499572bNnD52dnfProzzPwzAMbNsmHA5TUaFmPlDsSJ1Ou5w5k/mgrXiWXM6jqipAU1OQu++Os2JFLbZtYNsGwWCxAcStrrwDlOUSNA1ino1lmPhAoeDjecXFbXML3UREFppt2VRHqqloqCAeijO8fhiAlVUriQVjJa5uaUsmk+zevZuuri6i0aim74nc4pqbm3nkkUdoaGggGAwSDAavO7GSSqX4wQ9+wIsvvsj69euJRCLE41r/fq1iEw6fM2fSDA3lGR7OkUq5xOMBKistmppCdHRECAZNQiGDWMwikQgQjVrzTdikqKwDlBfwCBoGMe/q08znPTzPJxBQgBKRxWUaJuFAmA11G9hQt6HU5Swbtm2TTCZJJpOlLkVEloBYLMa2bdtoampienr6utGn6elpjhw5wrPPPsuuXbvYuHHjh6b33apc12d8vMDwcJ7x8Tyzsy6BgEk+7+H7kEgEqKsLEotZ1NYGqK8PUlUVIBjUqP+nKesA5Zs+tmEQ5upCv+IIlI9lFYciRURERGRpq6io+Mhpd57nMTg4yM9+9jNCoRB/+Id/yPbt2wkGgyWosnQKBY/ZWY+pKYeZGYdCodg0bWbG5cqVAjMzLoWCTyRi0tQUYsUKm/r6IMnkja8Dk6vKOkB5podlGNj+1SR9dQTKxLaVsEVERESWq5mZGbq7uzlw4ADf/OY32bhxY9mvb5rrkpfJeORy3geXXS5fdhgczDE8nCOb9QkGDZqbQ6xeHWblyjA1NQpLC6WsAxQGmEDgmgBVbMfI/GI4EREREVl+fN/n5MmTHDhwgGAwyBNPPMGKFStKXdaCurZL3pxs1uPSpTzHj6c4cybN6GiBeNyirS1MR0eEe+6poq7OVrfpRVTeAeoD1/745PPFIU3LQmugRERERJYp13Xp6emht7eXJ554gurq6rLbn6lQ8BkdzXPqVIaBgQzDw3kAGhqCtLWF+epX64jFTILB4syqYLDYKU8NHxZX2QcoA+M3ApSHaRbDkzo7iYiIiCxPw8PD9PX1YZomDz30EKFQqCze2/W8cZH+CwUmMxaObxEOm9TU2GzfXoFpGpimQSxmUlUVoLIyQDBoaLTpJiv7AOXj413zeS7nYZrGBwGqZGWJiIiIyBdgmiamaTI1NcXrr79OOp0mkUjMBynHcUilUkxMTDA0NERnZyddXV0kEolSl349z8PLZJl8o5tfvZgj7GRorCpgBgLEKiwarSArQkHCYRPTAHLARKmLXkZaW6G6GhaoO2PZByh+IyTlcj6WVdwHSkRERESWp0QiwbZt2+jp6eG5557j5MmTRKNRwuEwhmFQKBRIp9OkUinGx8d5+OGHaWtrW5IByi04pIYmeetfuslOV7J9ncPOliyBwAfr+DPAQCkrXOYqKqCyUgHqRviGj4HBtbNh83lPm+iKiIiILHPRaJT9+/fT3NzMz3/+c44ePcrw8DD5fHGdUCAQIB6P09TUxKZNm+js7KSqqqrEVV/PczxmLqc5eWiEI5P1fHWvzbq1YQLhsn6bfnNVV4O9cF0Iy/qV8UyPgAG2fzVCZTKe9oASERERKQNVVVXcdddd3HXXXUCxa10ul8PzPGzbvm7T3aXG930yV9KcfOMiT/3kAn/+Vxtp2d6CXREpdWnyCco6QM1vpOt/eCPdYge+EhYmIiIiIotibhPd5dBQopApcOzXl3jrxff5r3++jsbNzQSiCzPNTBZP2cYIx3NwTZegYRLzrj5Nx/HnO5iIiIiISPkwjOXTZTmbyvPmLwZ4//gldt2VoGN3K8F4GMM0P/3GUlJlG6AyhQyO7xD0TaL+1adZKPgYhqEmEiIiIiJy0/m+j+f4HHrxAhePX2RlS4jN968iUl1R6tLkBpVtxJ0tzFLwCgR960NT+IojUGgESkRERERuKt/3KeRdTrxxkd6D52isM9m+t5V4W32pS5PPoGwDVM7J4XouNibBa/rwua6PYYBGR0VERETkZvF9n1zW5ULvFQ786CgdjR5b962icm1zqUuTz6hsY4Tru/j4GIB5zWZQvg+GgTbRFREREZGbxvdhqG+aH/75G+xszbD1kS0k168sdVnyOZTtGqiAGcDEpAA4+B/6t+LiQiUoEREREVl8nudz8q1hXn/qOL/dPsn2/7yfypW1y6bhhXxY2QaomB0jYAaYMVyyhjN/vWEUzwD4/ifcWERERERkAfg+HP/1JU79oodmxrnjv+whsaoWK7i096iSj1e+ASoYwzZtcoZL+poAZZoGnlechyoiIiIisphOvz3K2Vd6CedTbPvyeup3rC51SfIFle0aqFAghI1NBo9pszB/fSBg4Hk+nqcAJSIiIiKLw/N8LpyZpOe5HoKpSTbf10bLA9tKXZYsgLINUAYGVsEi47pcMXPz1wcCxR9o11WAEhEREZGF5zoeU2NpfvnUCazBAbbsbaPjd7apDXSZKOtX0SpYpD2PK2Z+/jrbLk7hc90SFiYiIiIiZWt6Istr//cUs4eOs/0P7mDVb29SC+gyUrZroAAChQAZ12PSujoCFQxaOE6BQkEjUCIiIiKysC4NTPP28+8x+NJRvvw/f4umHW0YQVsBqoyU9QiU6Zg4HmQMB++DVuahUHENlOMoQImIiIjIwhkdnOHka+cYPXaBfd/YRNOONoKVUYWnMlPWI1CmZ+L74OCR911CQCRi4roKUCIiIiKycMYuztJ98H3GesfYuLOG9Q9ugFhU657KUFm/ooZnYPgGju+R9ovroMJhBSgRERERWRi+7zM9VeD465d4v/sSDc1hbv/qBozKSgzLKnV5sgjKOkBZroXpmhRwSflZYC5AQaHgaS8okU/g+75+R0RERD6B5/lkMy4nj1zm5KvnWNVscc/vtmPW1pS6NFlEZR2gTNfE8AwKuExfE6AACgU0CiXyCTzPw1W7ShERkY+Vy7qcPTnN8//7MHd2+ex+qA2rpanUZckiK+s1UIY/N4XPJeMVN9ONRk0CAcjnPbJZD9su6wwp8rm98847PPfcc/T397Nnzx7uuece2traiEajpS5NRESk5LIZl3Onp/jXJ9/m9/aGWLuvC7ulAUMNI8peWQeoQrCAa7sUfJcZL4vjOURjJoGASS5XDFDxeKmrFFmaVq5cyZ49e6iurmZwcJAf/OAH1NbWsnbtWjZv3kxnZyeRSKTUZYqIiNx06bTL6Xcv8+7zZ7m//Qpr77uNitZ6jFCw1KXJTVDWASofyVMIFRh0J/lF9jh3uHliMZNAwCCf98lkvFKXKLJkNTQ0kEgk6Ojo4PTp05w+fZqZmRn6+voYGBjgtddeo6WlhdWrV7NmzRoqKyt11k1ERMpeLufRf2qC3l/201gY4c5HOwmvacYMh0pdmtwkZRugXNfFNVxMA/JengvOZVzHIRIxCAQgm3WZnXW0xkPkE9i2TUtLCy0tLezbt4/BwUG6u7s5fPgwhw8f5syZM/T39/Pee+/R0NBAfX09dXV1JJNJDMNQoBIRkbLh+8Uuzn2npul99TyRy5e4/0v1RO7YWurS5CYruwDl+z6e5zE4OEj2/SxVY0F20MDXKndw6cIlLo+7FAo5JiYK9PXlMNWbX+QzWbduHWvXrmV6epq3336bI0eO8OMf/5iKigp2797Nfffdx7333kttbS2W2reKiEiZ8H0YHXY480ovqzOD/Nb+eiJ77yl1WVIChl9mfYodx2FiYoLHH3+cw0cOU+85rAiHmbRDzNpBDKOGePy/AS6ZzPMUCkdLXbLIsjR3ssLzPAqFAplMhnw+T0NDA48//jjf+c53SCQSpS5TRETkCxsaushf/uX3cS4/wCNeN3c9vpXqR/djBMpuLEJuQNm96pZlkUwm+eEPf8iTTz5JVSTC7335yyTr63GAfN7iRz9ySKdd7rtvJ7t2ld23QGTROY7D6Ogov/rVrzh27Bjnzp2jubmZ3bt3s3v3bjZt2kRFRUWpyxQREfnCHMdndibM5f5tPGYfYts3f4uqvTsUnm5hZffKG4aBbdusX7+eFStWUFFRwZpNm2hubsb3fVwXamv7GRsr0NhYy7ZttaUuWWTJm9tUt6+vj2PHjtHT08PIyAhVVVXs37+furo6mpqaaGlpoaGhgbjaW4qISBlwXY+BvlkO/utZ7h49Qte37iZxZxeBGs2wuJWVXYD6JIZRbCARjZp4XrEFpYh8NN/3SaVSDA0N0dfXx/nz55mdnSWdTpPP52lpaWH9+vWsW7eOVatWEYvFrruPyclJpqenCQQC1NTUEA6HS/BMREREPjvfh4G+Wbpfeo/coTcJ1w0Tvq0DqyYBapJ0SyvrAGUYBqZpXtcJrKIigOtmmZpySlSZyNI3NjbGyZMnOXbsGAMDAwwNDbF27Vq2bdvG1q1bWbNmzcc2iXBdl/7+frq7u7l8+TK2bVNTU0NTUxObN2/Gtm116BMRKRHP87hw4QKTk5OlLmVJc/Jx3js4wtjBI0Rz7/BK0qduoI8pXJ0QXCaCwSCdnZ1YlrWg7zvKOkAlk0ni8Tih0If78ldVBXBdj8uXC/i+rzdyIh/h9OnTvPDCC1y5coW9e/eyZ88eampqsG37E2/neR7T09P8wz/8A93d3SSTSTKZDGfOnGHlypX89Kc/pbq6Wr93IiIl4rour7zyCkeOHCl1KUtWasYlN7KKLVemaK4Y4q0Gl2PHzuA8/TSJRIKA1j8tC9XV1XznO98hGo0u6P2WXRe+a01MTBAIBIjH4x96s/bqq5P8+7+PU1Nj8xd/0Yptq5W5yG9yHAfHcfB9n0AgMH/25tOCz8zMDIcPH+Z73/se3/ve97jrrrs4d+4cTz31FD/5yU84dOgQra2tanEuIlIic1O0c7lcqUtZsv7pR0NUHnyFnbuTtH9tN0NOgSeffJInnniCjo4OIpFIqUuUG2BZFlVVVQu+N2VZx+eP+4bt3BmnvT2CZRlYls6Ci3yUQCDwuc6wTU5O8tprr7Fv3z5Wr15NLBYjGo0Sj8eJx+NEIhHtvyYiUkKGYcz/3ywfNj1V4Pl/H6Hu3bfY8WA7q/dvJtTewszICOFwmHg8TiKR0PduGVno8ARlHqA+7gx3ZWWAeLz41DWLSGRhpdNpent7efTRR0kkEhiGwdTUFFNTU2zZsoVgMKjpeyIiJaYTWdcbG8tz9I1xZl56k7t3Jlh133qiq5shFMKyLEzTxLKs+UNuXbfsb49hKDyJLAbP88hms4TD4fk/0KOjo4yMjLBv377r1iSKiIiU2vhYnlOHR3j/4Gm2teZY8+AmKta2gJpFyEe4ZQOUiCyOcDhMW1sbPT09jI6Oks/nCQaDrFy5kgceeIBgMFjqEkVEROZNTzmcevcy517vZ6V3iV2PbyPatRo+YnsOESjzKXwicvNVV1ezf/9+/vqv/5rq6mps22b79u1s3bqVmpqaUpcnIiIyL5fz6Dk+xZnX+qidvsi+R1pg82ZNU5JPpAAlIguqqqqK+++/n2w2y9/+7d9y6NAh/uiP/oh77rmn1KWJiIh8SHd3iqPPnWZ17jz3/cca0N8quQEKUCKyoAzDIBwOs3fvXpqamnjmmWd49tlniUaj3HbbbaUuT0REhFzOY2Agwxs/O8vmzFm23dtI8O5d8Cl7HcrSlMvlOH78OEeOHGFkZASApqYmtmzZgmmadHR0UFlZuWD7dylAiciCM02TZDLJjh07mJmZ4eDBg7z88ssKUCIiUnLptMuFc2leefo8XeNvs+H+lSR2b8ZIJEpdmnwOV65c4c033+Tv/u7vMAyDYDCI7/u88847/Nu//RsAf/Znf8btt99OVVXVgjymmkiIyKIJhULs3LmTxsZGjh07VupyRETkFpfJuJzvn+WdlwZY8c7L7Ly9irq7N2E0NZW6NPmcxsfHeemll+jv72fz5s08+OCDPPjgg9x22234vs+LL75IX18fmUxmwR5TI1AisqgSiQThcJgrV66UuhQREbmF5fMeFwbSnDg4SPbQOzyyYZLg7zyG0dhY6tLkC0in0wwODtLe3s7Xv/51urq65vegvOOOOzh37hyRSGRB96DUCJSIfGa+73/o+CSu6+L7vjYdFBGRknFdn0uXchx59SKTv3yH3295j+D/+otieFLHvWUtGo3S0tLCe++9x9jYGPl8Hig2tbrzzjv54z/+Y7Zs2UJFRcWCPaYClIh8Zr7v4zgOnud96tdOTEyQzWapq6u7CZWJiIhc7/LlAs/+7BLuS6/wyKoLxL77P0Abu5eFxsZGHnvsMSYnJ/n7v/97jh49Ov9vlZWV/Omf/imbNm0iGo0u2GNqCp+IfGYXLlzghRde4MCBA9x+++3ceeedbNy4kdra2utGmk6cOMHIyAgbN24sUbUiInKrcl2f6WmXf/k/QzS89Qt2bg+QeOxRjMrK4siTRp+WvUgkQmdnJ9/97nf5x3/8R376058CsGvXLkzTJBKJLPhjKkCJyGdWVVXF1q1bAZienubXv/41zz//POFwmFWrVtHc3Ew0GmVoaIi33nqLeDzOvn37Sly1iIjcSlzXY3y8wLPPjFL/5gG2bY3R/NAOrI7VYGoS1nKTzWa5fPky9fX1BAKB+TVNpmlSWVnJV77yFSYmJnj99dd5+umnSSQSdHZ2LkotClAi8pklk0nuuOMOtmzZwunTp+nt7eXs2bNMTU0xMDDA6OgopmkyMzNDMpnk9ttvZ/369aUuW0REbhGe5zM2muetV0dwXniV29bkaPkPuwluWq+9npahmZkZuru7+fnPf05dXR21tbXU19dTU1NDVVUV8XicRCLBY489xqVLl+ju7ubgwYMKUCKytJimSTQaZceOHezYsQPHcRgbG+Ps2bNcuHCB2dlZurq62LJlC62trQu2eZ2IiMgn8Tyfy+MFet4a4dyzR3g4cZrGR3+f4Pq1Ck/LVDqdpr+/n5dffplUKkVtbS3Nzc3U19eTTCapqalhxYoVVFVVEYvFyOVynD17dtHq0TsaEVkQgUCAxsZGGtUOVkRESsT3fVIph0O/GqPv6bf5Mv+Plf/9G5hrO2ABmwjIzbVixQoefvhhtm/fzokTJ7hw4QL9/f2cOHGC8+fPMzU1hed5eJ6HYRhs27ZtUddeK0CJiIiISFnwPPjF85eZfe6XPBjuZdV/+l2Mrk4IBktdmnxB0WiUzs5O1qxZg+d5uK6L4zjza6Pef/99pqeniUajrF69mvb29kWrRQFKRERERJY13/fxPHjmmXGcN95ia0OK1vvuxtqxrRie1G1v2TMMg0AgcN2SAM/zqK6uprW1FcdxsCyLcDhMaBHb1CtAiYiIiMiy5fuQTnu8/PIkqdffoSs4QseuFsK7tkNlZanLk0VmmiahUGhRA9N1j3nTHklEREREZAH5PkxPOxx7+wrnXjvNWvc863Y2UHX7RqitLXV5UqYUoERERERkWZqZcTh7appjr5xna7qbjTuSJO7eBm1tpS5Nypim8ImIiIgsd75/9ePcep+lsu7n2trmLv/m53OXP+q637yPDxR8i9PHZnn31fdZkzrD3U0T2Hu/DC0ti/yE5FanACUiIiKy3Hke5HLgOMWmCTdxPcgN8X2YnS0e+Ty4bvFjLgfZLKTTkMkUj9nZ4sdstnjMPa9CofjxA0dnWzg1EacydYX6FTmMb38LqhMlfJJyq1CAEhEREVluUik4cwYOHChe9n0IBMCyiuEklyteV1EBjY3Q1ATJZPGIxYpfZ5rFUJJOF+8jkyneLpWC6eniMTtb/JpCoXi/n4fvFx/LtovH3GNbVrHmuevnLodCxbrnPres+dt4pkUmC2cH8hw64XNuapaqYJzkbe1srEwUv05kkSlAiYiIiCw3hlEcadqwoXh5LmTMBahC4eoUONcthqKpKXjvveJo1dxUOMO4GmbgariJxYod7Ezz6vVftN65kHRtgJoLUdceweD8Zd+yGJ/0uDhcYHjUZXTcJRK1CCUDrN5rse6+AtEINHbUYtrW0pm2KGVNAUpERERkuQkGi2t92tshEvn4gJPJwOQkjI9fHVXKZouhyveLtwuHIRq9OvUvEimOAEWjxcvXjgQtMtf1yWQ8xsbyXB4tkE57ZLMeuZxNBhc36mNVWTS1hmhtDZNIBLBt9USTm0sBSkRERGS5se3idLxPE4kUj6amxa/pMyoOkPnMzLhksx7ptEsu55FOewwOZhkdLTA97dDQEKKjI0Jra4iGhuLaLg00SSkpQImIiIjITeH7Pq5bHGlyHJ983uP48VkGBrL09WXIZl1aWsJs3hzj3nsTVFYGsCylJVlaFKBERERE5KbIZDzOncty/Pgsvb1ppqYKdHREaW8Pc/fdVdTW2gQCBrZdPDTSJEuRApSIiIiILDjfh1TKYWgox/nzOXp709i2STIZoKEhyKZNUSzLoKLCIhazqKiwCAZNhSZZ8hSgREREROQL8zyfbNb7IDBlGRsr4Ps+sVgxGHV1RQmHLZLJAHV1NtXVagAhy5MClIiIiIh8LrOzLpOTBS5fdpiedjAMmJlx5xtDRCImtbU2jY0hVq4MEQhohEmWPwUoEREREflUnueTz/uk0y6plEuh4DM15TA6mufixRyTky7JZIC2tjB79lRQW2trhEnKkgKUiIiIiFzH9308r9gxz3Uhn/cYHc1z6lSanp5ZxsYcGhsDdHXFuP/+JKtWRTS6JLcEBSgRERERuU4+7zM0lOPEiVlOnUrjOD51dTatrSG+8Y0GwmFzvlueRprkVqIAJSIiIiLkci5DQ3n6+jIMDeVJp10qKiwaG4M88ECSWMwiHDaJxSwSiQCWBYaGnOQWpAAlIiIicgvKZFzGxgoMDuYYGcnjeT6GYRCNmrS1hTAMiMcDrFhhU1NjEw5bmqInggKUiIiISNnz/eJapsnJAmNjhfkuebmcRyrlksm4mKZBbW2ANWsiNDeHCIU0LW+ObdusWrWKiooKLMsqdTlSYobv+36pixARERGRhZXPe8zOuqTTHvm8Tz7vMTxc3NR2fLxAKGSyalWYDRuitLWFMQxDI0wfI51Oc+rUKdatW0csFsM0FS5vZQpQIiIiIsuc73+4a57vw8hIju7uYgOIsbECwaDBhg0xdu6soKUlTCymkRSRz0MBSkRERGSZ8zwYHc3R05Pm5MlZhoZy1NbatLdH6OiI0NBgEwya2LZJKGRgWQamqeEmkc9DAUpERERkmXEcj+lpl5Mn01y6lOPKFYdg0KC2NkhNTYBo1CISMYnHLeLxAJGIqcAkskAUoERERESWsOL0PBgeznHxYo5Ll/JMTzvEYha2bRKJFNfjRKMmdXVB6ups4nFLLcZFFom68ImIiIgsMY7jMTPjMj5eYHraJZfzmZ11SKVcpqYcCgWfeDxAe3uYlpYQsZiFZSkwidwMClAiIiIiJTTXYjyddslkip3z8nmPiYkCFy4UO+bNznqsXVtcz9TaGiKRsEtdtsgtS1P4RERERG6iubdengeeV+ycNzXlcPx4it7eDEePpohGTTZtirFjRwVdXRVEIoam5IksEQpQIiIiIjeR7/vMzLicOnW1Y55pQmdncT+m+vog0ahFMGgQCpnYdnF/JgUokaVBAUpERERkEXkeXLqUY2Agy9BQjqGhHJWVAWprberqbGIxk2DQpKoqQDxuEY1qPZPIUqYAJSIiIrKAHMcjlXIZGsozNJQjlXJxXR/DKO6/FAwaxOMW9fVBVqywqawMKDCJLCNqIiEiIiKygFIpl/7+DENDeVIpl2zWI5kM0NQUorExxMqVoVKXKCJfgAKUiIiIyAKanXWZmHCorbW5994EFRWakidSTjSFT0RERERE5AaZpS5ARERERERkuVCAEhERERERuUEKUCIiIiIiIjdIAUpEREREROQGKUCJiIiIiIjcIAUoERERERGRG6QAJSIiIiIicoMUoERERERERG7Q/wcYup1MEBsFjAAAAABJRU5ErkJggg=="
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
"To proceed in small steps we consider two shapes of constant bond-slip law, referred to as **bond-hardening and bond softening**.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The increasing/hardening or decreasing/softening trend of the bond-slip law in the second branch introduces the question, what kind of **material structure** within the bond zone can induce such type of behavior. An example of an idealized bond system leading to hardening or softening can be provided using a rough surface with an increasing or decreasing number of asperities. A more detailed classification of the bond systems will be shown in Tour 3 which provides a more physically based description of the debonding process. The question studied in this notebook is **what is the qualitative effect of the second bond-slip slope on the pull-out response.**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# **Numerical support necessary**\n",
"\n",
"To solve a pullout problem for a generally nonlinear bond-slip law, we have to solve\n",
"the initial boundary value problem numerically. In this notebook, we will use a finite-element code\n",
"implemented within the BMCS tool to study the behavior for two examples of qualitatively different bond-slip laws. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Solution algorithm:** To study of the effect of the nonlinear bond-slip law on\n",
"the pullout response we will use the finite-element method solving the nonlinear response of the pull-out test by stepping through the loading history. Let us therefore briefly touch the topic of the solution algorithm needed to solve such a nonlinear problem boundary value problem of continuum mechanics. Generally, a non-linear finite element solver includes the solution of two separate tasks:\n",
" - **Time stepping** algorithm that can identify the material state variables satisfying the constitutive law for a prescribed loadincrement in all points of the domain using an iterative Newton-type algorithm.\n",
" - Find the **spatial distribution** of the displacement field satisfying the equilibrium, compatibility and boundary conditions using the finite-element discretization."
]
},
{
"attachments": {
"fcf8bea4-2c06-4931-b39d-47e53c0d6dda.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAngAAAChCAYAAABUOcL0AAAABHNCSVQICAgIfAhkiAAAABl0RVh0U29mdHdhcmUAZ25vbWUtc2NyZWVuc2hvdO8Dvz4AAAAqdEVYdENyZWF0aW9uIFRpbWUARnIgMDcgTWFpIDIwMjEgMTY6MzM6MzMgQ0VTVA5A+XEAACAASURBVHic7d19XM33/z/wx6lUFCFlhWT6mKyNuQxphMllLNlcjC9mxrDMkrCxfWYfYi7n+iLKjPlkM2ZECmGGbCEXK4pKV1S6vji9f3/4nfNxdC7r1Km3x/12c7vlvN/n/XqenJxHr/frQiIIggAiIiIiEg0jQxdARERERPrFgEdEREQkMgx4RERERCLDgEdEREQkMgx4RERERCLDgEdEREQkMgx4RERERCJjYugC9CUrKwtSqdQgbZubm8PS0tIgbRMRERG9SDQB79GjRygsLDRI2zY2Ngx4REREVGvwFi0RERGRyDDgEREREYkMAx4RERGRyDDgEREREYkMAx4RERGRyDDgEREREYkMAx7RcwRBwBdffIHz589Xy/W/+uorREVFVcu1iYiIZESzDh69fG7evInY2Fi155iamsLW1hadO3eGmZmZxmvOnz8fbdq0Qe/evfVVpgI/Pz+8++67+Oqrr9CjR49qaYOIiIgBj+qshIQEXL16FZcvX8bp06dhbm6ODz/8EBYWFvJzcnJyEBkZieTkZMyePRtLliyBqamp0uvt3r0b8fHxWLlyZbXV3KBBA+zevRv9+vVDeHg47O3tq60tIiJ6eUkEQRAMXYQ+xMbGGnQnCwcHB4O0TcCWLVswY8YMeHl54ZdfflF6jr+/PwIDAzFhwgSEhIRUOJ6amopOnTohOjq6RkLXtm3bcOzYMZX1EhERVQXH4FGdd+7cOQBA//79VZ7z+eefAwD27t2L69evVzi+ePFijBs3rsZ61KZMmYLo6GgcO3asRtojIqKXCwMe1XmRkZEAgL59+6o8p379+vKvb926pXAsOTkZe/bswbRp06qjPKVMTEwwZcoUrFq1qsbaJCKilwcDHtVpd+7cQUpKCqytreHi4qLyvMuXL8u/fvXVVxWOBQcHo127dnB2dq62OpUZOXIkIiMjcf/+/Rptl4iIxI8Bj+o0We+du7s7JBKJyvMOHDgAAHB1dUXXrl0Vjh06dEirGa0PHz5ESkqK1rWVlJSoDW8dO3aEtbU1jh49qvU1iYiItMGAR3WaLOD169dP5TmxsbEIDg6GnZ0dfvjhB4Vjubm5uHbtmtqAV1JSgjlz5iA4OBhjx47FkiVLKpyzfv16uLm5KTzm7e2Ntm3b4vTp00qvK5FI0LlzZ/kYQiIiIn1hwKM6Td34u/Lychw+fBgDBgxA165dcfHixQq3Z//++29IpVJ07txZZRsrVqzAmDFjsGjRIri7u+M///kPSkpKFM7ZtGkT0tLSFB6rX78+BEFQu7Cxo6Mj/vrrLw2vkoiISDdcB4/qrFu3biE1NRXAsx0ijIz+9/tKQUEBEhMT0a5dO2zbtg1Dhw5Vegs3ISEBANC0aVOlbeTl5eHOnTv44osvAAAXLlxAvXr1YGxsLD8nJSUFd+7cwaRJkxSeu3PnTkRFRaFZs2YqX4O1tTUSExNRXl6uUD8REVFVMOBRnfV879327dsVjpmbmyvMnFUlPT0dAGBlZaX0eFRUFLy9vQEAjx49QmRkJLy9vRUCnuwW7Ntvv63w3IYNG6J///544403VLZvbW2NkpISPH36FI0bN9ZYLxERkTYY8KjOej7gNWnSpFLXkN1qVRWuPD095V8fPHgQ5eXlGDNmjNI6Xgx4wLOdNLp06aKyfVm7DHhERKRPvCdEdZIgCAozaKtKm11QDhw4AAsLCwwZMkTh8YiICLRq1arC+D7gWU9igwYNVF6zuLgYALTaJ5eIiEhbDHhUJ928eRPp6ekwNTXVaokTVaytrQE860FTJzMzExcvXsSwYcMUAltKSgru3bunNGReuXIFrq6uaq+bnZ0NAGjUqJGupRMREanEgEd1UkREBACgS5cuanvINGnZsiWA/wUtVW7cuAFBECqsoRcfHw8AeP311ys8Jzg4GO+9957a62ZnZ8PGxkar8YJERETaYsCjOkkW8Kp6e7Zdu3YAnu2Ioc7jx48BAHZ2dgqPZ2RkAPhfUJTJy8tDcXExWrRoofa6cXFxaN++vU41ExERacKAR3VOQUGBfPzdi4sL66pt27awt7fH1atX1Z7n6uqKevXq4e7du/LHpFIp9u/fDwsLCyQlJSmc//XXX2PevHka2798+TJ69+5dueKJiIhU4CxaqjPmz5+Pa9eu4Z9//kFWVhYA4PPPP8f333+PmTNnYsSIEZW6roeHh8aA16JFC2zduhWLFi1Cq1at4OTkhP3792PGjBkYMWIEAgIC0KJFC7Ro0QJHjx6Fp6envHdQlUePHiEpKQkDBgyoVN1ERESqSARBEAxdhD7ExsZqNROyOtjY2MDBwcEgbb9M8vLyUFpaqvSYpaUl6tWrV6nrhoeHw8vLC2lpabCwsFB7bk5ODi5duoScnBy4u7ujefPmAJ7dqr148SJKS0vRt29f+eQNdYKDg/Hll1/i3r17XOSY9KasrAyCIFT650FXpaWlkEgkMDFhf0FtUFhYWCfG9BYVFcHc3NzQZYgaP1WozrC0tESTJk2U/qnKh5mHhwfs7e3xyy+/aDzXysoK77zzDnx8fOThDngW8keMGAFvb2+twh3wLOBNmzaN4Y70JiUlBe+88458h5eaanPw4MFITk6usTZJOdnC7FKp1NClaLRlyxYsWrQIIuljqpX4yUIvPYlEgsDAQKxatarG/rO5cuUK/vnnH8ydO7dG2iPxS0pKQr9+/bB48WK0atWqxtpt3bo1vvnmGwwcOLDCWFSqOadPn8bUqVOxbds2hZ12aitfX19kZWVh9uzZhi5FtBjwiACMHDkS9vb2CA4Orva2BEHAvHnzsHLlyiot8UJ1w/Tp0yGRSLT6Y2RkhGbNmqFnz55YunQp0tLStGqjqKgIo0ePhq+vLzw8PKr5FVXUo0cPLFiwAKNGjUJBQUGNt/+yi4+Px4QJE3DgwIEKM/prsw0bNiAmJgYbNmwwdCmVMmDAABgbG6Np06Zo2rQprK2tYW1tLf+7ubk5GjZsiPv37xukPo7B0wOOwROHjIwMDBs2DD/88AOcnJyqrZ01a9bgwYMHWLNmTbW1QbVPWloa+vbti9u3b6NRo0a4ceOGQk+bIAjIyMjA3bt3sX37doSEhKBRo0bYu3cvhg0bpvbaM2fOxN27d3Hy5ElIJJLqfikqeXl5oXnz5ti2bZvBanjZlJWVoXv37hg+fDi++uorQ5ejs/j4eHTq1AkREREV1hmtC8rKypCSkgIXFxfk5ubC0tIS+/fvh6urK5o0aWLQITjswSP6/2xsbBAcHIxPP/0UOTk51dLG0aNHERMTg1WrVlXL9an2srGxkY+N69+/f4XbqBKJBLa2tnBzc8OePXswb9485OTkwNvbGzdv3lR53WvXrmH79u1Ys2aNQcMdAKxYsQJ79uzBpUuXDFrHy2Tz5s1IT09HQECAoUuplLZt22LGjBmYMWMGysvLDV2OzkxMTGBiYoLc3FwAz37JGTp0KKytrQ0+vpoBj+g5r732Gnbt2lVtA8YbNWqEXbt21YkxMqRff//9t3zHlH79+mk8f+LEiQCAkpISBAYGqjzP19cXI0eOxBtvvKGfQqugffv28Pb2xqxZs+rkh3Vd8/jxY3z11Vfw8/Or0zNS/fz8EBMTg127dhm6lEo5e/as/GttfrZrCgMe0QuaN2+ODh06VMu13d3dDd7LQoYh230FAPr27avxfDMzM/nXqtZpjIyMxNmzZzF9+vQq16cv06dPx5UrV3D69GlDlyJ6GzduRH5+PiZPnmzoUqrExsYG3t7eWLFiRZ2cVStbeB9gwCMieunIPgSaNWsGFxcXjeffvn1b/nWTJk2UnrNz507Y2dkZZGKFKu7u7rC3t8eOHTsMXYqolZeXIygoCMOHD0ejRo0MXU6VjRkzBnFxcQphqa6Q1ezg4IBXX33VsMU8hwGPiKiaSaVSnDt3DgDQp08frXpxNfUKPH36FKGhoRg4cKDBx/o8TyKRwNPTEz///LN8x5mqKCsrw+HDh+Hn54dZs2Zh5cqVCuFXWxEREXqpp7aIjIxEQkICBg0aZOhS9GLAgAEwMzNDUFCQoUvRSUpKinwvc2165mtS7flfgYhIpGJiYnQaf1dSUoJ9+/YBeHb76tNPP61wzrlz51BYWKhT793du3cRERFR6UlEly5dwqNHjzSe5+bmhpKSEoWxSZVx48YNvPnmmxg5ciRWrVqFjRs3Yv78+XB2dsaQIUMQFxen9bU2b96sdrJKXRMWFgag8rcEi4qKcOnSJRw/fhwxMTEqdwmqKZaWlujUqRPCw8PVnhcXF4dTp05VCOuCIOD69es4ceIEHj58WJ2lKjhz5oz8awY8IqKXjK7j7wIDA5GWlgZzc3Ps379f6e4osh7Bjh07arxeSUkJPvjgA6xfvx7Hjx+Hk5OTypmu27dvh6OjI6KiohQeX7FiBVxdXeHq6ori4mK17XXu3FmhxspITk6Gh4cHUlNT4e/vj7CwMFy6dAk//fQTxo8fj/DwcLz++utYvHixxiWycnJycPLkyUovZ3Xr1i14e3vD1tZWvsaZuj8tW7bUKXxWxtmzZ9GoUSOdbwkWFRXB398f7u7uOHr0KB48eIDQ0FC88847OHbsWDVVq5233noLKSkpiI+PV3p8w4YNWLhwIc6cOYPWrVvL6/3jjz/g6emJPXv2ICYmBu7u7pg8eTJKSkqqvebnA97bb79d7e3pgpsHEhFVM23H35WXl2PVqlVYunQp7O3t8eOPP8Ld3V3puX/++SeAZzNXNfH19cWQIUMwduxYFBUVITAwEAsWLFAInjKBgYFITEys8OF47do1AMCDBw9w584dvPnmmyrbk9VUleVSvvnmG9jb2+PkyZOwsbGRP969e3f4+Phg4cKF8PX1xbJlyxASEoJVq1bBx8enwnVyc3Mxbtw4ODs7VyrgnT9/HkOHDkVubi7s7OzQsGFDAM/WzbSwsFC6WPm//vUv2Nra6tyWtqRSKa5evYpOnTrp9Lzy8nKMGjUKxsbGOH/+vMIWjwUFBejRowc6deoEe3t7fZesFWdnZwDP3jdt27ZVOPbw4UMcOnQI4eHhMDIyQlBQEKZNm4bVq1cjODgY+/fvl49V9fLygrOzM4yMjLBz585qrbm2jr8DGPCIiKrV8+Pv3nrrrQqr2peVlSE5ORmXL1/Grl278OjRI8ydOxeLFi1C48aNVV733r17sLKy0rg8RmxsLJKSkjB27FgA/5u8kZiYWOHcpKQkxMXFwcTEBD169FA4tmHDBly8eBEPHjzQOObPzMwMtra2SEhIUHueOqGhoQgLC1MId8/r0KEDwsLCEBoais8++wxjxoxB165dMXbsWLz++usoLCzE1atXsXXrVuTn5yv0tGgrNTUVY8eOxYwZM+Dn54emTZvKj3Xr1g1bt26V91bWpOTkZJSUlOgcIoOCgnD8+HHcu3dPIdyVl5fD09MTN27cwN9//22wgCfbhUPZ+yYkJASzZ8+Wv/fy8/ORnZ2N7du349ixYzA1NZWf265dOzg7O2P37t1YuHBhhbCoL7V5/B1QxYC3aNEimJqaauyup7rHzMwMS5YsMXQZotOvXz8MGjQIPj4+1fafDtUuz4+/e/DgQYUlTWQLHNvZ2SEwMBAeHh6wtLRUe83S0lIkJSWhRYsWGttfv369Qps///wzACjdNUDWo9e1a1dYWFgoHLOxscHSpUsxdepUrXrCbG1tERsbi5KSEoUPX22UlZXBxMREqx4qb29vDB48GMuWLcOaNWswb948heMODg44ePBgpXZJmDx5MpYsWYKpU6cqPJ6SkoLr169rNRu6OsgCkLpfAJQJDQ2FsbExmjdvrvB4QUEB/vzzT9jY2KBLly76KlNndnZ2AJQHvNDQUPkvSunp6cjOzpb30Cl7fzVt2hTl5eU4duwYZs+ejdGjRyMpKQmPHz/GrFmzlI5r1VVVl0f573//iw0bNuDJkyeoX7++vFdeX6oU8KRSKcLDw3HlyhV91UO1hL+/v6FLEKVr164hMjISAQEB6Ny5M3x8fBj2RO7526CbNm3Sy5ImBQUFkEqlsLKy0nhuTk6OwkzLH3/8EQDw/vvvVzhXtnadqtvCnTt3Rrt27bRalqNx48YoLy9HXl6eQs+XNkxMTHRa9LZBgwZYtmwZ5s+fj99++w13794F8KzHdPDgwToHTADIzMyEh4dHhXAHAL/++itef/31Sl1XH2S7Jmjz7/+8Bw8eQCqV4rPPPsO3334r/3extLTEP//8g4YNG+ocGvVJ9ovN06dPFR4vLi6Gi4uL/Ha4bPJOx44d0bp1a6XXku3jLJtwsWrVKmzevBmBgYF629b0+UlElenBGzBgAFq3bo1BgwbJb/3rU5Vv0RYVFRlsD1iiuiw6OhrR0dEMeyIn+y3fzMwMPXv21Ms18/PzAWj3AS8LdMCz99w///wDS0tLDB48WGWtqj6snj59qvVrkN0CrEzAAwBPT0+Fvz98+BBPnz7Fq6++ivr16yt9jpWVFcaNG6f0WH5+Pho0aKD1QuPNmjWDn5+f0mNHjhwxyK1Zmby8PADQORR069YNN2/exNatW7Fjxw507NgRb7/9Nry9vdG7d+/qKFUnsn9X2euTMTMzw549e+R/l71PVfWaFRUVyXsBZT3Rjo6OGDZsmNpdYXT1/Pg7R0dHrZ5z9epVODo6wtraGo0bN0a3bt3wr3/9S76NoT5xFi1RLSALek5OTujSpQuWL1+uciYZ1R3Pj7/r1q2bymCiK1l40nVpiwMHDgAAhg8fXqGW+/fvIyEhASYmJnBzc1P6/D///BMDBw7Uqi3ZJI2qbMsnCAI2bNgABwcHODg4wMXFBZaWlhg4cCCOHz+u07UWLlyol1tgeXl5CA8PN2jAk/37l5WV6fS8wMBA9OrVC8Cz92Z0dDTWrFkDNzc3fPHFF3qvU1dFRUUANL9nNP0icu3aNfn7r02bNvLH9bmLUGXH333yyScVxrBWV08wJ1mQXkVERCAzM9PQZdRa2nwgs2dPPJ7ff1afg7Bl25jpup7dTz/9BAAYPXp0hWOy27Ndu3ZV2TMUHh6u0JOijux1axpPqIogCJg0aRJCQkJgbW2NESNGoGnTprh37x4iIyNx6tQpeHl5Ye3atVr1npw9exb/93//V6lanhcWFobi4mKDBjzZxJoXb2VqYmNjg/Pnz+P8+fMICwtDVFQUzpw5A6lUimXLlmHQoEEqw31NkK1tp+49k56ejtjYWBgZGaFPnz5Kz5GtESiRSDBgwAD9F4rKjb+7ePEi7OzsVO5Mo28MeKRXX375ZYX1s6jyGPbqtuc/BPQZ8Bo1agRLS0udAl5cXBwSEhJgbm6u9PasbCy1qvF3spmbqma1vig7Oxv169fXeZyYTFBQEA4cOIDVq1dj+vTpCsuRpKenY9myZdi0aRPCwsKwYMEC+Pn5qewh3bdvHxITE/UyKeLXX3+FiYmJ2mVisrOzkZGRgcePH6Nly5Zo2bIlCgoKcPPmTRQWFqJ9+/YKM2CfPn2KGzduoF69enjttdc0jnGUTUbQ5d+/qKhIHgx79+4tvyWbmJiIYcOG4caNGzhx4oRCwKvu1/Ei2etRNzs4MjISgiCgU6dOKscLHjp0CMCz4KVuRnBqairu3LkDMzMzdOzYUace9soscLx27VpMmjRJ7TllZWW4du0a8vLy0LZt20qv3QjwFi1RnREdHY1ly5Zh8eLFldqqiWqeLOCZmprqbfydTJs2bXT6gJft4uDs7Kz0g+zevXsAoHIWZUhIiMrxbcrk5ORoPS5Jme+//x6rV6/G3LlzK6w1Z2tri3Xr1iE6Oho9evTAkiVL0KFDBwQHByuM30pPT4efnx8mTZqEhQsXKiwNUhlSqRS//fabyu+hzMSJE9GtWzf07NkTR44cwc6dOzFz5kxER0cjIiICTk5OWLx4MQRBwLfffov58+fj5s2bOHDgAFq1aqVxuy7ZbUdZL6k6RUVFcHd3h4WFBfbv31/heOvWrbF06VIAqLCg9sSJE9G1a1f569ixY4fC62jbtq3C6/D399fpdbxI9nrUrSenafzd3bt3ERMTAwAqbzs/evQIEyZMwPLly5GQkICIiAh07twZfn5+8tvEmsgCnqOjo1bv86ioKJw+fRpDhgxRec7GjRvx3nvv4Y8//sC9e/cwd+5c9OrVq/ITWYUq8Pf3F7p16yYA4B+R/Vm6dGml3hNubm4Gr11sfywtLYX3339fCA0NFQoKCqryI0s1qKysTGjcuLEAQHBzc9P79b29vQUAQnJyslbnh4aGCgCEQYMGKT3u4uIiABAiIyMrHCsrKxN69+4t5ObmatVWRkaGAEDw8vLS6nxl7VlaWgrFxcUazy0vLxf27dsn2NnZCQAEU1NToV27doKDg4P8Z2jChAmCVCqtVC3PO3v2rABAmDRpksZzjx07JgAQBg4cKAQFBSkcCwgIEAAIU6ZMEcLCwhSOvf/++0L9+vWFzMxMtde3tbUVnJycNNZx8OBB+fdh/fr1Ss8JCgoSJBKJ8Pfff1c4duTIEa1ex8mTJyv1Op73zTffCACE48ePqzzH2dlZACDs3btX6fGZM2cKAISpU6dWOHbu3DkBgNCiRQshPj5e4diTJ08EZ2dnwcPDQ+P7Ljk5Wf491ea98PDhQ6FVq1bCJ598ovS47HPz22+/rXBsxYoVgrm5uRAeHq6xnRfxFi3p1WuvvcZZ1Wr89ddfkEqlGs+ztLTEsGHD4OPjg8GDB+ttcD7VnCtXrsh7JFSNFaoKNzc3hIaG4tatW1otTCu7pfjiQsvAs97hW7duAXjW6/WiTZs2wcfHR+vxdLLewsqO5zIyMsLIkSO1GnwukUgwduxYDB8+HNu3b8dPP/2Eu3fvQhAE9O/fHx9//LHSMYeVcfjwYQDQavydbBzj06dPK4z9k+30UVRUVGHSSvv27bF//37Exsaqfd+4ubnh8OHDCrdelSktLUWLFi0wbtw4fPTRRxWOS6VSrFu3DuPHj1d621l2GzQ3N1fl6yguLq4w1k3b1/G869evw9jYWGVvd2pqqvx9evnyZYwfP17h+Pnz57F161b07t0b69evV9nOhAkTKvQSNmnSBAsWLMCkSZPw3XffISAgQOXzT506Jf9a0/ZkJ0+exJQpU5CUlIQJEyaoPVdZm76+vli7di0mT56MO3fuaFzY/HkMeKRXO3bsMHQJtVrjxo1V3lZr2LAhhg4dylBXh8XHxyMlJQWZmZlYvXq1/PH79+/j1KlTaNy4MZydnSssIlwZsrFyFy5cQP/+/TWe7+TkhEmTJmHPnj04ceKEfG289PR0zJ07F0eOHMHo0aOxefNmjBw5Un478/Dhwzh//rzCciuaXLx4UaFGXUkkEoSEhOj0HEtLS8ydOxdz586tVJva+P333wGovo2tTPfu3Ss8ZmLy7KNX2eLLsgk0miZQ9OnTB4cOHcIff/yhdgzY8OHDsWbNGgwePFh+bZnMzEx88sknaNasGbZs2WKQ1/G8S5cuoWPHjirH7snWlOzQoQP+/PNPXL9+HW+88QaAZ7dAR4wYgSFDhmDv3r1Kt5CTUTWbVnbbd+fOnRXC1q1bt5CWloZHjx7h3//+t/zx/Px8XL16Vf73wsJCZGRkIDY2FkeOHJFv19euXTu4urpq+hZUYGpqil69eiE0NBQnTpyAl5eX1s9lwCMyoIYNG8p76jw9PRnq6rgFCxbIe+2srKzke6NmZWVhxYoVKC0txXfffaeX3QI6deqE1q1bIyIiQuslLrZt2wYnJyfMmjULzs7OsLKyQkpKClavXo0uXbrg7Nmz+Pzzz9GlSxd07twZ6enp6N69O/bu3avTEhORkZFwdHSs1O4RtVV5eTmSk5PRpk2bCtu4qaMuzOvSG/MiLy8vzJs3D5GRkWoDnqWlJY4ePYoVK1Zg+fLlsLe3h7GxMR49eoTS0lKMGzcOEydO1Lj9nLrA9GJwrIyEhAQkJCRg2rRpKs+RBby+ffvC398f06dPR7NmzZCZmYnHjx9jw4YNGDduXKWXQ5FNXomPj1fYgUUqlWLOnDnyWb5WVlbyn+Hdu3dj9+7dKq/ZpUsXmJqaYubMmZWqCfjfFm6yBby1xYBHVMMY6sTr4MGDNdaWkZERpk6diq+//hoZGRlazW41NTXF4sWLsXjxYhQWFiIrK0vh9m6XLl0QEREhP9asWTOd1+h68uQJIiMj4e/vrzE01CVGRka4d+8eGjRoIO+5MqQ2bdrAw8MDhw4dkk+SUMXW1hbfffcdgGc9Trm5uWjevLle14WrKtk2ahMnTlR5jizgvf3223BwcMDvv/+O7OxsmJubVyksy8jWzrOwsFB43xsbG+PkyZNVvn5lyRY213VWcpXepa1bt8awYcN06jKkukHXBTRJO/v27UO/fv0Y6kgvJk+ejH//+9/Yv38/Zs+erdNz69evr/J9qO6YJgcOHEB5eTkmT55cqefXZpXZkaM6ffTRRxgzZgxiYmLULtvyPAsLC70MEdC3kJAQDB06VN5b9aKkpCTExcUBUBz3ps+t1WRjR5UtI2RIt2/fhrGxscKWg9qoUsDz8vJSOmCX6j513fFUeeqmyBPpqmXLlpgzZw7WrVuHGTNmGLxnSSqVYu3atZgzZ06VlkgRk/Lycp3OFwRB63O9vb3h6uqKVatWITg4WNfSdKJLXbqef+rUKdy8eVPpMi4ysuVR2rdvj+bNm+tUy4tkQe5F33//PSwsLBTG2NWkO3fu4LXXXlN47OrVq7hw4QJ8fX11/5nSed4tERHVGjk5OYK9vb2wa9cuQ5ciBAcHCzY2NkJOTo6hSzGo8PBwwdfXVwAguLq6Cr/88ouQlZUlCIIgnDx5Uhg/frx8GZlff/1VKCwsFHJzc4UTJ04IHh4eAgDho48+UrtciMzly5cFU1NT4fbt23p/HefOnRM+++wzAYDQs2dP+esoLS0Vjhw5IowbH11kZAAACUtJREFUN04AIIwcOVLhdRw+fFjr11FeXi707t1bmDNnjtpapkyZIr9eVV5PvXr1hIULFwoff/yxkJ2dLQiCIGRlZQmffvqp8MorrwhRUVGVvn5lubm5CR988IHg6ekpb18qlQonTpwQWrRoIXzyySdCWVmZzteVCIKOsZyIiGqVw4cPY9q0aYiNjUWzZs0MUkNmZiZcXFywadMmvPvuuwapobZYvnw5CgoKYGFhgZKSEuTn5+Pjjz+Go6MjFixYAHNzc9SvXx9FRUUoLCzEggULUFRUhLVr16JBgwYwMzNDQUEBJBKJxvF1ADBv3jxcvXoVEREReh1Xp+p1vPLKK1i6dKleXsfWrVvx3Xff4cqVK0rHmJWUlCAxMRF9+vRBWloaFi9ejNmzZ6vd7UKVhIQEnDt3Dh988AEuXbqEnTt3oqCgACUlJejbty8mTpxY6a31qmLLli3w8fGBmZkZ1q9fL98pxNHRERMmTKj0tngMeEREIvD111/jypUr+PnnnzVu1q5vUqkUI0eOxFtvvYWvv/66RtumZ9//IUOGoG/fvmrXb6ttYmNj4enpiRMnTsDZ2bnC8fz8fLRt2xalpaUK6/GVlZVhzJgxGpd2edkx4BERiYAgCJg1axaMjIywYcOGGm07ICAAOTk52LhxY62amfkyycnJwfDhwzFz5ky8//77hi5Ho4yMDHh6emLNmjWVXi+R1BPPHHYiopeYRCLBxo0b0a5dO8THx9dYuw8ePMArr7yCTZs2MdwZkJWVFU6cOIEbN27oPLHDEI4dO4bdu3cz3FUj9uARERERiQx78IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhERjQB77///S8++ugjg7S9a9cufP755wZpm4iIiOhFogl4JSUlyM/PN0jbxcXFKCgoMEjbRERERC8STcAjIiIiomcY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEhgGPiIiISGQY8IiIiIhEptYGvF27duHy5cuGLkPvEhISEBgYaOgyiIiISMRqbcALCgpC9+7d0aZNG8yfP79Oh72EhASsXLlS/nr8/f0NXRIRERGJmImhC9BEFo5WrlwJR0dH+Pj4wMfHB926dTN0aWolJCTg4MGDOHjwYJ0Op0RERFT31PqA97zaHvYY6oiIiKg2kAiCIBii4TNnzuCPP/5QeXzLli1ISEjQ6lru7u4YNWoU9u3bB29vbz1VqL2oqCjExcXh9u3bWj9n+fLlao+3bNkS48ePr2ppRERE9BIyWA9eYWEhsrKyVB4vKytT+3wHBweMHj0aPj4+6NGjB3788UeUlpaqvWZ1KSkpQa9evXDkyBF5D961a9fUPkdTnVZWVvoskYiIiF4iBuvB06RPnz6IiopSeOzFUCeRSOTH9u3bh99++w0//PBDTZeKzZs34/r169i0aZP8sbi4OLVhr5Z+24mIiEgEav0YPHWhrjZzcnJCQEAAAgICNIY9IiIiIn2qtQFv0qRJWLlyZZ0KdaooC3tERERE1aXWBrwPP/zQ0CVUC1nYIyIiIqoutXahYyIiIiKqHAY8IiIiIpFhwCMiIiISmVq7TIquUlNTkZmZCRcXlxpvOykpCXl5eWjfvn2Nt01ERET0ItEEPCIiIiJ6RvS3aIuKilBSUlLhcUEQkJOTY4CKiIiIiKqX6AOer68vXF1d0bBhQ0gkEkgkEjRv3hzdunXDiBEjkJqaaugSiYiIiPTqpblFO336dGzbtg1DhgzB0aNH6/ziyURERESqiL4HT+bChQsAAB8fH4Y7IiIiErWXogcvMzMTtra2EAQB9+/fh6Ojo6FLIiIiIqo2L0UP3tmzZyEIAhwdHRnuiIiISPReioAXGRkJAOjbt69B6yAiIiKqCS9FwDt79iwAoF+/fgauhIiIiKj6iX4M3pMnT2BjY4Py8nIkJibCwcHB0CURERERVSsTQxdQ3c6dO4fy8nK8+uqrWoe7p0+fIicnB8XFxXBycqrmComIiIj0S/S3aM+cOQNAt9uzS5YswZtvvol33323usoiIiIiqjai78HTdoJFaWkpCgsL0ahRI6xZswampqb4/fffq79AIiIiIj0TdQ9ednY2YmJiAGgOeD/88AOio6PlfzcyEvW3hoiIiERM1CkmKioKUqkUTk5OaNmypdpzf/nlF7i7u9dQZURERETVR9S3aLUdfxcWFob27dsr7bVLTU3F1q1bkZeXB0EQMGbMGHTv3r1a6iUiIiLSh5ci4Km7PZueno4PP/wQx48fr3Ds4cOHWLduHRYsWAArKyvcv38fw4YNw3vvvYcvv/yyusomIiIiqhLR3qLNysqSj6lTFfDOnTuHXr16wcbGBh06dKhwXCqV4ttvv4WVlRUAoE2bNtixYweWLFmiNBASERER1Qai68HbtGkTMjIycPr0aUilUtSrVw/BwcGQSCQAgOLiYqSlpeHChQv466+/AADr1q1Tei0jIyP582R69uwJU1NTBAUFwdPTs3pfDBEREVEliC7g2dnZyXvkZs2apfQcZ2dnhV69wYMH69RGw4YNkZaWVpUyiYiIiKqN6ALeqFGjqvX6hYWFyM7OhouLS7W2Q0RERFRZoh2Dpw9FRUVITk5WeOzAgQOwtLTEvHnzDFQVERERkXoSQRAEQxdRGwUEBCArKwtlZWUYNWoUWrZsiZMnTyIkJARbt26Fq6uroUskIiIiUooBT4UnT57AwsICxsbGiIyMRGJiItq2bQs3NzeYmIjuzjYRERGJCAMeERERkchwDB4RERGRyDDgEREREYkMAx4RERGRyDDgEREREYkMAx4RERGRyDDgEREREYkMAx4RERGRyDDgEREREYnM/wOlaRaAELkMegAAAABJRU5ErkJggg=="
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/bus.png\" alt=\"Diver\" width=\"40\" height=\"40\">\n",
" <b>Short sidetrip</b> </div>\n",
"\n",
"## Time-stepping - Newton method to solve a set of nonlinear equations \n",
"\n",
"The Newton method is the basis of all nonlinear time-stepping algorithms used in finite-element codes. \n",
"Let us explain the solution procedure by considering a very short bond length $L_\\mathrm{b}$x and denote it as a material point $m$ for which a constant profile of the shear stress $\\tau(x) = \\tau_m$ and slip $s(x) = s_m$ can be assumed.\n",
"\n",
"\n",
"\n",
"The iterative time-stepping algorithm with increasing load levels can now be displayed for single unknown displacement variable $w$ which must satisfy the equilibrium condition $\\bar{P}(t) = P(w)$, where $\\bar(P)$ is a prescribed history of loading. A simple implementation of the time stepping procedure exemplifying the solution procedure for a nonlinear equation is provided for an interested tourist in an Annex notebook [A.2 Newton method](../extras/newton_method.ipynb). \n",
"\n",
"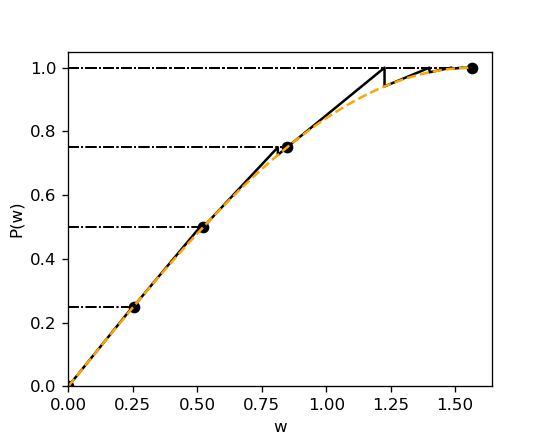\n",
"\n",
"In a real simulation of the pull-out problem, the unknown variable is not a slip but the displacement fields $u_\\mathrm{m}, u_\\mathrm{f}$ are the primary unknowns. They are transformed to corresponding component strains $\\varepsilon_\\mathrm{m}=u_{\\mathrm{m},x}, \\varepsilon_\\mathrm{f}=u_{\\mathrm{f},x}$, and slip $s = u_\\mathrm{m} - u_\\mathrm{f}$. In the following examples, the component strains are still assumed linear elastic while the bond/shear stress is assumed generally nonlinear. With the known stress fields, the corresponding forces are obtained using numerical integration which deliver the residuum of the global equilibrium condition. The solution scheme described for a single variable in the notebook [A.2](../extras/newton_method.ipynb#newton_iteration_example) remains the same."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/diver.png\" alt=\"Diver\" width=\"40\" height=\"40\">\n",
" <b>Deep dive</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Spatial solver - boundary value problem solved using the finite element method \n",
"\n",
"The identification of the displacements within each equilibrium iteration includes the same conditions that we have applied to derive the analytical solution of the pull-out problem with a constant bond slip law. However, the discrete solution satisfies the equilibrium conditions only approximately in a _week sense_. This means that the local differential equilibrium condition is not satisfied everywhere but only in integration points."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To provide an insight into the way how do the finite-element tools solve the problem, an open implementation of the nonlinear solver used in this and later notebooks is described completely with a running example, plots and animation in a notebook [A.3 Finite element solver for a pull-out problem](../extras/pullout1d.ipynb). This notebook is an Annex to the course and is meant for ambitious adventurers who want to see how the most finite-element programs available on the market are implemented. Detailed explanation of the theoretical background is provided in the Master's courses on linear structural analysis focused on the theoretical background of the finite-element method and on the nonlinear structural analysis."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/binoculars.png\" alt=\"Traveler in a hurry\" width=\"40\" height=\"40\">\n",
" <b>Distant view</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example of the finite-element pull-out simulation\n",
"\n",
"To understand the functionality of the finite-element model implemented in the referenced notebook [A.3](../extras/pullout1d.ipynb), its output is provided here in form of the pull-out curve and of the fields along the bond zone. The applied boundary conditions are given as follows, the free length $L_\\mathrm{f}=0$, the matrix is supported at the loaded end."
]
},
{
"attachments": {
"image.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAABnCAYAAADmM/4PAAAABHNCSVQICAgIfAhkiAAAH+JJREFUeF7tnQm0VdMfx7cpKtMKUSHzSqUkylT9F1ZFk1qtZkMStaRoVBSeUCpllSkJTUSqpcJKxiYKGSpSCqEkQxkS0v99trWv8847595z7z3n3HPv+f3WOuu9e4Y9fPc5+7d/495nbzEpIUFAEBAEBIFYIrBvLHstnRYEBAFBQBDQCAgTkBdBEBAEBIEYIyBMIMaDL10XBAQBQUCYgLwDgoAgIAjEGIH9Y9x36boPCOzcuVPNnj1bl3TMMceoH3/8Uf3555+qcuXKqnHjxj7UIEVEEYE33nhDffHFF+rwww9XZcqUUdu2bZMxj+JAeWiTSAIeQJJb3BEoV66c+t///qcWLFigLr30Uj0h8PvMM890f0iu5D0CNWvWVFu3blWtW7dWEyZMUPXq1ZMxz9NRFUkgTwcuKs3ef//91ZFHHqnmz5+vTjjhBNW2bduoNE3aESACjPnPP/+sa2jXrp2qXr16gLVJ0UEiIJJAkOjGpOzVq1erP/74Q9WuXTsmPZZugsAHH3yggRCpL7/fB2EC+T1+kWi9TAaRGIbQG/Hhhx9qm0C1atVCr1sq9A8BYQL+YRnbkjASQtgChOKBwKeffqptAn369FEHHXRQPDpdoL0UJlCgAxtmt1gRQqIWCBP13NZlpL+rr746tw2R2rNGQJhA1hDGu4Bff/1VbdiwQUsBqAbcaMaMGapBgwZul+V8niEAE8ARgCMZbd++XfXu3Vv16tVLj//ff/+d7Ha5lgMEhAnkAPRCqnLJkiX6w7799tsdu2VURZ06dVIwDKHCQGDhwoWqUaNGjp35+uuv1bfffquvdezYUcePFBUVqVGjRim8yYSihYAwgWiNR961hkme1aCTPYAAIqQEO7E6JMhMKD8RYExRATqNOT169tln9cQPcS+xJBUqVFDnnntufna4wFstbLnABzjo7qEWcHMNnThxourQoUOiCUgM6JArVaqkMCw2adJE9ejRI+gmSvk+IzBt2jT1zz//ONqAiB347LPP1L777qvGjRunYwlefvllrSoU+4HPA+FXcewnICQIZIpA8Ypvb7EqqNTjixcv3lscRbp3z549iWvcu2nTJv2b88XRpnvHjh1b6lk5EV0EGLdTTjllb7FH0N5du3aVaChjXhxJvHfq1KmJ88VSooxxdIdTt0wkAb+4aYzKYXU3adIknTsG90D+3nHHHRoBcgetX79erwa7d++uV4SGuNcYEjl/2WWX6Xu6dOmio46Foo3ACy+8oLAFINERGzBixIhEg9euXavee+89rfq5/PLLo90RaV0JBIQJyAuRNgKI9v3799fPkTcmUzJGQjEWZopguM+1bNlScWQz5uG2WGrzgoAYhr2gJPf4ggDZRU2+GQp87bXX1KBBg5K6lvpSsRQiCAgCrgiIJOAKjVzwGwGiS+fOnatVSKiN2rRpI6oDv0GOUHmoj6pWraqdAFAXSZK5CA2OpSn7YBiIZtOi3yomNNF/Rn+cCq2FeOZYbS3o6PHAad68eaF1Nef9Ibbl4IMPTrQD+xd4FxvHc942vxog6iCPSD755JMl7sQ/PlmErMdi5TZBIG0E8MMnIMsQRvqzzz477XLkgdQIjB49usRNzAOFxADonDCB1O+BvoMVgCGzq5JbsIzHIuU2QSAjBEjbzWqU45FHHtEeVyY4K6MC5SFPCMAACjHWQWwCnob/v5t4EfjoCvFlSBMKuT2HCMAA8NIhGE8YQLADwQLQMADj4hxsjeGWLkwgDbyTpUhIoxi5VRDIGoHJkyfrxGzCALKGMmUBMAATB5Py5jy8QQzDLoNm8qWby7wI2ADEEOwCmJwODYE5c+boRGwtWrQIrc64VsTkj9RvlQDwbiukPEhiE3B5u63+7EgA5MgRBuAClpwOBQFUQBiBMQqfc845odQZ10qMCghJy64CIt6FsSgU8qwOIlzcpIdN1vnifDGh+gMzGEzObHTuJxlOjwRgDMBiCPYTYSkrHQSMDQBvFdxBeT/tk1M65cm97gjAAAwTQBIo9O/esyRQsWJFxYq4a9eu2kjCC2gO8r48//zz+hq6yjBp+PDhasGCBYHkqhcbQJgjKXUlQwAJQIzAyRDy75oxAvtXYrRL8iwJsHWg2VD6uuuuK8UdSQbWt29fBbMIi9599101ffp0XR0RqNagjmzbYNxAxQsoWyTl+WwQMCogFlxiBM4GSW/Pxo0BgIpnSYCbmRihiy66SP+1EhGMqGWOP/54+6VAfhM1iYrqrrvu0uV7UVV5bYjppzAAr4jJfUEhwKTEd9W0adOgqpByixHABmhUP3FTs3mWBHhT2E3IviJBP2le0K1bt4a2Wlm2bJnC/mBSEFsNudm+1YWuA8wWH3k+PASuvfba8CqLcU14/hWyG2iyofUsCTDBc3Tu3DlRHlvHPfPMM4nfrFjCcp1atGiRlkhQUSGFoA4SEgQEAUFAEEgPAc+SgFGRoHdHRDUh61YmgP9sGPTiiy9qmwSTP3VWrlzZV3VQGH2QOgQBQUAQiAICaTGBRo0aqVtuuUXvL4oL1YoVK0JPpkRWvyVLlqh77rkngV+VKlUUm5oLCQKCgCAgCKSHgGcmgD2gfv36unRW4CeddFKJeAAkg9WrVztuPp1ek5LfzXaEZL+26u927NghTCA5bHJVEBAEBAFHBDwxATPB9+zZs0QhbApiaMqUKeq0005zrMSvk3gD1ahRQ1144YUlikQy8NMw7Fd7pRxBQBAQBKKOgCcmwAofNUzjxo1L9Me4g/7+++8KI/E111wTWH8J1cYuYVUDmcqwEbz11luB1S0FCwKCgCAQJgKo27NxVSX3GXElXvY88cQEyJtDgW7BKhMnTtTumpkSUb81a9ZMmpuHrersTMjUV65cOfXDDz9kWr3n57CJCAkCuUYA+5dsIpPrUQiufvaLGDdunD4yJRjIbbfdpuyb4jiVl5QJ4BKKmmXWrFmaAcCdrPTRRx+p2bNnq9dff12tWbNGu5CyyQV7iR566KH698aNGxURxkT3IjHwTFFRkSpTpowuClUTAV+s9D///HNta7ASz2OApkOonKyEdLJ9+3b12WefaZsAEsuxxx6ruR9h9iNHjlS33nqrjiSmDALKevXqpf+yyTnnYUD0ES+jVBHHJjCtRCPkhyAQMgIzZ87U3xYLJ6FoIsC8xH4P77//vtq5c6dWYZP5FcKmylxIKnA8G+1000036ewL2RDzGQsFdqFr165d0qKSMoG3335bT5Bt27bVhRg3UWuJuGoSWcsEytGwYUOFZDBjxgzdWbyJRowYoQExZaC+MRk5AWbVqlWKc4gwdibA5A1nhAlYt9SjLCZzgsaQEDhgNDAGYhUIsrn77rv1PUOGDNGiFZkXqZf+AP55552nunTpovtIX3kWot2outhGrlatWpqhQTAYIUEg1wgcdthhuW6C1J8CAYJYhw0bpo4++mh1ySWX6MWmlaZNm6YdbRYvXpxQ++B1yYKZeccP+yq5ppjrWJQnWzAkZQKZpE5mAqUT/IXgSNY9OVHd2I24NLJfv356QrYTHXEjgEoFlsl3ZLiwaYuJaUASgUtbjc0MxldffaXtHEgUcHIY4E8//aQZAS6p1FuhQgW3psl5QUAQiDkCaD2QCAYNGlQKCVbpLGrHjBmjxo8fr6+jcSER5/r160vdn+kJFugsdr/88kvX+SopE8i0YjPhmuftv+3lIgE0adLE1eZgvz+d34YZpfsMkgMHXBzCJfXKK6/UEsM777yjhg4dqg488EDVqVMnLf2IlJAOwnKvIFD4CGBLRTVN8k07GdX6EUcckbiE3ZNJ26TCsT+TyW8Wt2g4UH8bjY69HN+ZAKtoDkP23/YG8BsmgK7eT6JeOm9UPKz4IfMbFRNk/nqtG1UTR58+fdT333+vPv74Y/XKK69oacEQ6qPTTz89YRvxWnZc79u1a5cqW7as5+6ne7/nguVGQcBHBGACuLQ7EZPyGWecofr375+4vHTpUjV16tRStzNnYXslNQ6LTpOpmbkLm8P555+vnyGPG0zHmrqH36jscaMPhQmgPmGlTOPWrl2rG83kC9cDEIzBHIhB3GtUM5monUohZTtBaotRo0bp+qkP28ETTzyRqBf7Ab8xJmea7+ioo45yzKgKQ6D/iHZW5oBxvWrVqurkk09WPBt32rRpk/aAQBWYTvZZxvSpp55SV111VdwhlP5HGAFUyHaPRlTh2EtRFRH3ZJxRUBsx2dtjoOgeqXmQELBpMm8a++rcuXO1CskwAeY85l7OW6lbt27qoYceckXKV0mASR0jrJXsnbrvvvtcG+PnBXvMApZ4K/kteVjLRhIwEoP1PAZw4hkwEu3evVs1b95cG4cyZUJ+4pWLsnBfQ82WLkM85JBDtGEfJj9gwIBcNF3qFASSIsBCBY/J3377Ta1cuVLfi8YDGyWqb1btVoIJOHknwhiwX1IeC+lWrVolHuO31VWYOQ3vTDuhqt6yZYv9dOK3r0zAtRa5oBGoU6eOPlAlISXh2vrNN9+oBx54IIEQL0Lt2rUL3g8cry+M6+kyAAPUxRdfrCU5ROgLLrhA3jBBIFIIoGFg4mbXw1TOKzSc+cApsAsmQLZkvCchNu8yhCrI6krKwuiss84qhQNMwO6MY71JmEApyMI5gWeRkwTwyy+/qM2bN4fTiBzWghrIiLWZNAOD/2OPPaZtScIEMkFQngkSAVRBGHi9MADaQZyUE5kAXWKk0KqYoFwm9eXLl5dQH7GotKufKBPHHBOX5VTHv36cTlfkXE4QQNWBy2wh07x587QhOFsX2/Llyyu8K1CzCQkCUUIAJoBrplfC2GucVpyeISAX25kh4gzwXrSqkNwCCLHJJvM4EibghHjMz2HMRgTFE8G+Wc/8+fOzRufpp59OBMg4FTZw4EC9ujf5oLChYD9xmuyxQ6EbFRIEooQAWZfTWczhGIFdwI2QFKyuptgbrO6lPOdkU+A8tohKlSq5FZ3eHsOupciFgkIA74XnnntOB8fhfWAIz6/Bgwdn1VcMZXhm4SVlJxgO9hGivfFwgBlQX7NmzfSqCmO/cfU1z1IOHhNCgkBUEMAdk2BTr6og2s0ETiAttgQnqlu3buJb5B5ilEizgzcQizZcTd3yt2GXsAbs2ssXm4AdkZj/5uXlheHFQsdonXRxQXMyPKUDGYbwPXv2OKqCXn31VW00h4jz2G+//XTkOcZ00n/gVWEPPMSYZk8nkk575F5BwC8EyF9mDLiPP/64Lha1EH76XqhFixbac9C6W6N5jjgBFmd8g9gJsKkRvMpvvBHxsnOSBGgT0juMwI2ECbghE9PzJriElw4yek1cWgmK69ixY1bIGPUSKxk7MckbYtJHx3niiSfqU0gDTsSLH0YGWae65ZwgYEUAvT7+/JkSKk8YARO8PWMzZZNYzkosyFItymBKuJg6GYxNWWITyHTECvQ5VhWstklshThrIh6RCiCiHLMhjLluZBL1cZ1gO8ieUND+LJJKOtHG9ufltyAQFQRIUcNCiPQRfhGRyXzLdgnaWr4wAb/QLrByyI9EBljjWoYeH8Jga9Qv2AjQ3X/33Xc6Nwlpa1EnMTEjBiO+klrDSmaFQ+qHZIReFXWQYToEu9iN1DyPR4V91ZSsXLkmCEQVAVbsqG6IofFDxQkzQbpItfdEzpkAHUa3hd7MfrRs2dLTeE2ePFmnmgZAIvHQk+FChWjmB5ieGlFAN+GJwORq9b9/6aWXdHQzgSfo7iF09Uz8ZCjEm4h0tWCOVw+h7ORPshuSCQ5j0raPCwbjO++8U0/01E8d5EE3wWSItVZJwcCN2kiYQAG9fDHvCit24meMbSFTODAeY1dLtZcA5efcJnD99ddrYyA+r0ziMAJj4HCKoLODgnWczmLMRF+NV4vRy5FSgAmC/QyEvCPA6h+vG5LjMdETlUsQGysKJusDDjhAF4Zen80xjF6SSZrfMASICRy9vp14Me0Bcbh5Tp8+Xd188806/xTucNQJIU0QDekk0rLp0KmnnmqvQn4LAnmLABIB+wpkQyzIku0hYC07p5IA4gougUzaTP54giC+GInAKQWrHRgmeFadMAOYQNOmTRO3EJFL4jih9BFgL2cCVDAQ//XXX3p1QsAJgV6MkSHc2qyTc7KgFPMMTADpwUowEnaBQw2FEfree+/VNgl20UIVZTUaW5/DVkFiLSFBQBDIDIGcSgJWdQ96ZLuKwEuXSBvAxENiOmteDZ5ldenkj27KJZKOAymEQ+g/BEyeIysmxn0zW5wIXMHgi58zGVUhjLv2rKA33HBD0qqQVJBGjAdR0pvloiAgCDgikFMmYG0RK81MdLtm5fnmm2/q7dwMESXHBN+6dWvHjnPSqJswYnKvExHJx8F19NXZpjpwqiNfz4E5OUxQ4yEdYAsgBoAU2iR4M3pNfuP6Zs1fgtqHjIes/jMhVEQEkzllTcykPHlGEIgrApFhAqiFnLZh8zIwTETonq3uhOiVoWSGEeMTn6wOvFQ4YALt27fXemrqQVWFugljqZPPe7IyC+Vao0aNFIch0kxwGEKv6abbJOQd/FH/gGG6RAZREsjJjm7pIif3CwIlEYgEE2CDBSZZN59wdMJ4+xAV52QsRu1jfxavFZiKWyi11xfB7D+MzQEvJgyjpFOA6aC+Yg9ieyoDymaDadQeGEfN4bXOuNyHLYg8QuCUzqYyBIcRxCYMIC5vSn73E29F5ih29rLvrxKFnkWCCeDWiXHRLfqN6xgI8U5x2owedQ7+5IRbo1LCZ53oumRRcpmCT7ATBxNQMv9bfOdxXyRNAi+A3V+e+lEtde7cWRvE40jgSJ6gdAkpokGDBuk+JvcLAjlBgAUumg4OPH9wve7QoYNiR0UvjhRBNzoSTACDLp4gboAQA8BBOLUTMcn26NFDc1mkhqKiIqfbQj2HJMAhJAgIAoKAQQCNAjEwHNjFWNSiscilY0okmIAXn1YiUd2AMmlbiS/AvTQoSrZPZ1B1SrmCgB0BdpRC0sRWJRQsAkGmKScgE8cGgl1xpMB+yfzlNs8F1dNIMAEvncPzxMnIS9oCDMPp6JS91Od0D2onIUEg1whgE0G9yOJHKFgE9u7dm7QCL4tON89DUzAR8kTkc0AwAdTExh7plB00aaPSvJgXTIDNFjDw2rdII9gMTo3/OnlqrJ4paeIgtwsCgoAgkDYC9qBHpwJ27NjhdNr1HEyDBScOJzCAoI3JecEEsBU42QsINvOaX8gVcY8XjjvuOI93ym2CgCAQFwQ2bdqUsqt4NZIXKxXhHIMHEYtap/3HUz2f6fW8YAKZds7P50iGxu4+QRABVuh5yYFECoS4egsFgW0hlrlu3TqdS4n9qIWCRcDLJJ9NC5j48RZC1d2mTZuMAmazqZ9nhQl4RJD8RBx+EnEGqLSIRGZ7uGrVqvlZfGTLIsaCnD8NGzb03Ebuh1HyscSdSeJ3ngsDoufBKqAbWcX7TTDwVq1a6XcZVY9TYkS/60xWnjCBZOgEeI04BqJliXr1mu0vwOaEVjSMD2mHvD/pEC7EDz/8sE4UaLLEpvO83CsI5BoBVDy4gxIfECUSJhDiaJDjmzw7TGQEi7jFPYTYpNCruv/++7UXhJONJ1VjRo0apXr37q0zxWaSZypV+XJdEAgCAd5Xdg0L2sCbaduFCWSKXBrPLVq0SPt0s+JHAiBqMI4EBkRae0kR7oQPYnPfvn01hk6bcTs9I+cEgVwjEKaRN5O+ChPIBDUPz5DFdNasWdrNi1VAELpFD82I1C2k+0afnQ2xeRBBNtgIUBEJ5RcC5Aljjwr04dWrV8+vxhdoa4UJBDCwRAGS74jValxX/XZYmbgJcPIjFTc5mxYuXChMwA5yHvzGCQJ3SQ4kQjYPsm4ElQddKLgm+soEiNzlSEVMBE77xaZ6zut1Jl907mESyeLIdMr2ikxSRDIXCtEXJBvUMXgxGcLGQToP+2Y+Tv0mp5PbNpDYSJAQkJr4n/TT1InLLOVbN7ynbCYPmECcCPyNCowASQ6njLpRx8QaXEUfbrzxRjVy5EjtHhlFwm+/0Gmf4rDo5HHRaSBAlBtiOomRcIGyZvFkJYhnCKmDu3fvrhPCBUGswtmRirz/bH0YJDHhM/HDAHD7IhlU0HUG2R+nstmXgX4yOTdr1kxvC2lSdOClg3rGOpZM5ExYRHdb1TXkXaIcKxMx9Q0fPlzr+YmOJEW02WgeRtCtWze9A5k1nwrvGAkDyRYbR8pnF1HSv6Aa5VthL+qw8+TE8X1J1WdfJQF8lzGCsHk8ufedxDws5KlyaaRqtNt1Jh8YECtIxM4gJ+QNGzaoK664Qo0fP9514xS3dubTeRg7K3EOqGLFionmk7vGvlJiMmcj+k8++USv7o0Xz7Zt2xw9ehgzPIVMfhSYTZUqVfQqF2mOScI+USBFsqeDUP4hQGxIXJl3VEfLVyZAJ03WPTcPEFaHfOhBECqCsWPHqp49e2q1lN+bjrDKxdjLxIVKa8GCBb7ouIPAwq8yzf4NfLiEsxsbB/jCCK1ub/zmwB7Cpj7WXE87d+4sNZnTRiZ/k/MJxs37g8QBUZdTgi6xs5QeXaQj3n8YJJIUUlqug5BKt1LORBEB35kAK0d2+bL6caMPNhuwMBnYdwHzAxiiSdmUxtSLisavICwkF/z7mfhY+YZtb/ADn0zLgJEysaOSQZQ3RIxDjRo1SuilsREY/O0ZX4nyZXKyk5VRwzwgvKmSEcw4rlt6OuGCxw0qNZIoMvGzSIGxmt9Oz8g5QcAg4DsTQIds3fWJD58J1DCBZLtxZTosqH+WLVumevXqpYtADUTm0WwIaYWUDmvXrtUrWCb+TAKcsmlDVJ5dsWKFjvI1K3AmYXZJ6tq1q2aMYISaCGkBhoEaCEnQKg0y2bPSdyIWBqxg2ZgeNZDVr5pxtafroM64joUTfthksJGYlT/pR8ARaQCblZAgkAwB3/c1RE+MARjjDweifdDiOytU6+qRCQkddKaEFwYJ41i90gc+pjhPOjByq2THit/s4YD6BqaLgRhDH3/By64OhJE62YLA2aiDli5dqp8z7wtlO40j5fit6sv0XYnCcytXriwlXeOoMH36dE/eelHog7Qhdwj4KgmwCsSlD90xHzOrcSYM+4RguksEKQwD1Q2RoJkS4q9Vd8yEzerSTujzWeFT38CBA+2XtS4bSQY1EobNoJlXqQZE9AR6/wkTJuhVPl5e6J6Z7GEETNRGAkvWfAKDRo8eXeIWJAPGv0mTJtqG0L59ey1hoNoz74XTHsTov932o07WhkK8xrtPQj4mfSsZF2ywhDlHlZAieYd4F3jPWFDwG+keCTCMzaKiik1Y7fKVCaAnZvXMh2u8PWAEVuMhAwxTYDLBk4fVH7rLTIgXhVwyTPqoIAzt3r1bfxhWQrUzYMAArdueMmVKqepY/bNaZeUvVBIBJnxUekw4jCsMlIOx5CP1YoDEIQA1Eu+Dkaowrm/ZskWXy8oeOwJeSOi4mbjcdlRC8otj3iWn9xLsIHvcjcm06iRJOZWTi3OkU2HyRxLk3ahdu7b+RlEH1qlTRw0dOlQNGTIkF02LVZ2+MgHETyYM68eLd4n5zUAzmcAEMBaXL19ee5CgPsiE0EFjY7A/j3+5Xf+8ceNGPcnzcdjvp+44GXszwRp1kD1pm5uE51Z+8+bNFR++FWveDaudCF12shTTLB7YX9feFrc6C/18quDMoDzxssWVcSReaP369booFhJ8szAA3gHcy2WnwGxR9va8bzYBViS8kHBzK1kZAuoYdgJDp8sqkvvxJsr0RUWUdJrQsQlYPw5UC6gyTH2pPhxv0MldVgQYUyQ6mDvSlBPGSIgwgWyId6hfv37ZFCHPRgAB7ExTp05NSJG8N7wzLCJh8HPmzHF0KY5A0wuuCb4xASZzyClADLUNHz8r9Fq1amlOz0Cjc2d1blcnoNoh8jcZ4fVgjUi23ou6gdWiIURlVA+mPtH1J0M2s2uMI3p9bEAwAaeUBow5LrYwg0wYPyo7bE5IFEL/IgDuECtrK/HNQU7jUOLGHP3ge7SqiUkfgQrIPhfkqHmxqjZrdRCTO6tsY/TjIzX6eV5MdPO4/q1atUrnkTcvppUJWBFnhYAuEF0mOWnshiHqwzD54IMPqkcffbTEblzUjYoIgzPGw0mTJumVBUZjKxOI1QhHrLMsElAjwSzScRdG0kCqHDZsWMR6lNvmoD5hUYO0a92Zzkhi6arsctEbtAg4ZGAPMMQijwWDLNiCH5GsmQAGPbg3E64T4Wlj3DetHjxO93IOG8HmzZv1S0GuGTsxEcAcOOyGQ55lZVRUVJR4LKorIXu/4vTbyb6Qqv+Mq1n1pro3TteZJOvXr68XYlYmYOJboooZWoHBgwerxYsXaxUiVK9ePf0X54ExY8bo/EJCwSOQNRPgxQtib1wYgFPEb7INGjKZXIKHWGoQBIJFABdd7DFGTYZUsGbNGjVv3rxgK86idLPDHtoCpDzmEBNRjicfNgGhcBDYr1h/e0c4Vf1XC6t8XgLcNdFd1q1bt1QTli9f7ni+1I0eTiBu8pGwwuBFI/pVSBDIVwRwqmCFb6RcYjDKli2rZs6cqfCCwz5HDi1UoVEl1FR896h9cQ0mtmjdunU6Sy3uwfa4h6j2oxDa5Wsqab8AwSjMij8f9Jl+9VnKEQS8IoDNDdVqVFU9Xvsh90UDgazVQUF0wxpbEET5UqYgIAgIAoLAvwj45iLqJ6B2g6+fZUtZgoAgIAgIAv8hEEkmIAMkCAgCgoAgEA4CwgTCwVlqEQQEAUEgkggIE4jksEijBAFBQBAIBwFhAuHgLLUIAoKAIBBJBIQJRHJYpFGCgCAgCISDgDCBcHCWWgQBQUAQiCQCwgQiOSzSKEFAEBAEwkFAmEA4OEstgoAgIAhEEoH/A+y5WMhnsPX1AAAAAElFTkSuQmCC"
}
},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from IPython.display import HTML\n",
"html_video_file = open('../extras/pull_out_animation.html','r')\n",
"HTML(html_video_file.read())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## What constitutive law can induce such a debonding process?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A closer look at the simulated evolution of the shear stress along the bond zone in the bottom right \n",
"diagram provides an important phenomenological observation. The level of shear increases \n",
"at the right, loaded end in the first stage. After reaching the peak shear stress of $N = 2~\\mathrm{N}$, it \n",
"diminishes slowly to a low value of approximately 0.1 N.\n",
"\n",
"The constitutive law valid at each material point has thus a first ascending and second descending branch. Such kind of behavior is called **softening**. Constitutive behavior exhibiting softening has a severe impact on the structural behavior by introducing the phenomena of strain localization to discrete shear and tensile cracks, accompanied with stress redistribution during the debonding or crack propagation process. The pull-out problem can be conveniently used to visualize the correspondence between the **softening** material law and the structural response with a debonding propagation, as opposed to **hardening** material law."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# **Setting up the model components - new material model**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the purpose of this comparison, let us introduce a simple piece-wise linear bond-slip law, that can be inserted into the non-linear finite-element code to investigate the effect of the type of nonlinearity on the pull-out response."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"trilinear_material_model\"></a>\n",
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/work.png\" alt=\"Coding intermezzo\" width=\"40\" height=\"40\">\n",
" <b>Coding intermezzo</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Construct a material model with tri-linear bond-slip law \n",
"To indicate how the below examples are implemented let us define a a piece-wise linear function with three branches constituting the bond-slip behavior. It can be used to exemplify how to implement material models in standard non-linear finite-element codes for structural analysis. In codes like `ANSYS, Abaqus, ATENA, Diana`, the spatial integration of the stresses and stiffnesses is based on the so called **predictor**, **corrector** scheme."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"This simply means that the material model must provide two functions\n",
" 1. the stress evaluation for a given strain increment\n",
" 2. the derivative of stress with respect to the strain increment, i.e. the material stiffness.\n",
"In our case of a bond-slip law, we need to provide two functions\n",
"\\begin{align}\n",
" \\tau(s) \\\\\n",
" \\frac{\\mathrm{d} \\tau}{ \\mathrm{d} s}\n",
"\\end{align}."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Let's import the packages:**"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"%matplotlib widget\n",
"import sympy as sp # symbolic algebra package\n",
"import numpy as np # numerical package\n",
"import matplotlib.pyplot as plt # plotting package\n",
"sp.init_printing() # enable nice formating of the derived expressions"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"The tri-linear function can be readily constructed using the already known `Piecewise` function provied in `sympy`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"s = sp.symbols('s')\n",
"tau_1, s_1, tau_2, s_2 = sp.symbols(r'tau_1, s_1, tau_2, s_2')\n",
"tau_s = sp.Piecewise(\n",
" (tau_1 / s_1 * s, s <= s_1), # value, condition\n",
" (tau_1 + (tau_2-tau_1) / (s_2-s_1) * (s - s_1), s <= s_2), # value, condition\n",
" (tau_2, True) # value, otherwise\n",
")\n",
"tau_s"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"The derivative is obtained as"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"d_tau_s = sp.diff(tau_s, s)\n",
"d_tau_s"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/evaluate.png\" alt=\"Evaluate\" width=\"40\" height=\"40\">\n",
" <b>How to get numbers?</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"**The above results are symbols! How to transform them to numbers and graphs?**\n",
"\n",
"`sympy` offers the possibility to generate executable code from symbolic expression (`C`, `Fortran`, or `Python`).\n",
"To get `Python` functions that accept the characteristic points `tau_1`, `tau_2`, `s_1`, `s_2`\n",
"and evaluating the above defined expressions `tau_s` and `d_tau_s`, we need the following two lines:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"get_tau_s = sp.lambdify((s, tau_1, tau_2, s_1, s_2), tau_s, 'numpy')\n",
"get_d_tau_s = sp.lambdify((s, tau_1, tau_2, s_1, s_2), d_tau_s, 'numpy')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The parameter `numpy` enables us to evaluate both functions for arrays of values, not only for a single number. As a result, an array of slip values can be directly sent to the function `get_tau_s` to obtain an array of corresponding stresses"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"get_tau_s(np.array([0, 0.5, 1, 1.5, 2]), 1, 0.1, 1, 2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/view.png\" alt=\"Evaluate\" width=\"40\" height=\"40\">\n",
" <b>How to to plot it?</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Let us now show that the implemented bond-slip function provides a sufficient range of qualitative shapes to demonstrate and discuss the effect of softening and hardening behavior of the interface material. Let us setup a figure `fig` with two axes `ax1` and `ax2` to verify if the defined function is implemented correctly"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"fig, (ax1, ax2) = plt.subplots(1,2, figsize=(8,3), tight_layout=True)\n",
"fig.canvas.header_visible = False\n",
"s_range = np.linspace(0, 3, 1050)\n",
"for tau_2 in [0, 0.5, 1, 1.5, 2]:\n",
" ax1.plot(s_range, get_tau_s(s_range, 1, tau_2, 0.1, 2));\n",
" ax2.plot(s_range, get_d_tau_s(s_range, 1, tau_2, 0.1, 2));\n",
"ax1.set_xlabel(r'$s$ [mm]'); ax1.set_ylabel(r'$\\tau$ [MPa]');\n",
"ax2.set_xlabel(r'$s$ [mm]'); ax2.set_ylabel(r'$\\mathrm{d}\\tau/\\mathrm{d}s$ [MPa/mm]');"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Preconfigured pullout model provided in BMCS Tool Suite \n",
"The presented function is the simplest model provided in a general-purpose nonlinear finite-element simulator `BMCS-Tool-Suite`.\n",
"The package `bmcs_cross_section` provides several preconfigured models that can be used to analyze and visualize the behavior of a composite cross-section. The analysis of the pullout problem discussed here can be done using the class `PullOutModel1D` that can be imported as follows"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from bmcs_cross_section.pullout import PullOutModel1D"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"An instance of the pullout model can be constructed using the following line"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"po = PullOutModel1D()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For convenience, let us summarize the model parameters before showing how to assign them to the model instance"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Geometrical variables:**\n",
"\n",
"| Python | Parameter | Description | \n",
"| :- | :-: | :- |\n",
"| `A_f` | $A_\\mathrm{f}$ | Cross section area modulus of the reinforcement |\n",
"| `A_m` | $A_\\mathrm{m}$ | Cross section area modulus of the matrix |\n",
"| `P_b` | $p_\\mathrm{b}$ | Perimeter of the reinforcement |\n",
"| `L_b` | $L_\\mathrm{b}$ | Length of the bond zone of the pulled-out bar |\n",
"\n",
"**Material parameters of a tri-linear bond law:**\n",
"\n",
"| Python | Parameter | Description | \n",
"| :- | :-: | :- |\n",
"| `E_f` | $E_\\mathrm{f}$ | Young's modulus of the reinforcement |\n",
"| `E_m` | $E_\\mathrm{m}$ | Young's modulus of the matrix |\n",
"| `tau_1` | $\\tau_1$ | bond strength |\n",
"| `tau_2` | $\\tau_2$ | bond stress at plateu |\n",
"| `s_1` | $s_1$ | slip at bond strengh |\n",
"| `s_2` | $s_1$ | slip at plateau stress |"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Fixed support positions:**\n",
"\n",
"| Python | \n",
"| :- |\n",
"| `non-loaded end (matrix)` |\n",
"| `loaded end (matrix)` |\n",
"| `non-loaded end (reinf)` |\n",
"| `clamped left` |"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Even more conveniently, let us render the interaction window generated by the model to directly see the structure and the naming of the parameters"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"po.interact()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The tree structure at the top-left frame shows the individual model components. Parameters of each component are shown in the bottom-left frame. By nagivating through tree, the parameter frame and the plotting frame are updated to see the corresponding part of the model. The control bar at the bottom can be used to start, stop and reset the simulation."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example interaction:** Develop some confidence into the correctness of the model. Change the stiffness of the components such that they have the same area and stiffness modulus. Run the simulation and watch the profile of the shear flow along the bond length. Increase the bond length, reset the calculation and run it anew. Change the position support and verify the profile of the displacements."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# **Studies 1: Hardening bond-slip law**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[](https://moodle.rwth-aachen.de/mod/page/view.php?id=551816) part 2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## RILEM Pull-Out Test revisited"
]
},
{
"attachments": {
"image.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUAAAAEuCAYAAAD/bsuAAAAABHNCSVQICAgIfAhkiAAAIABJREFUeF7tXQd4VNUSnhASEnqT3nsv0nsRpChFsaGCNEWfKKLPgsgDRERERUQUEQQUxIo0pUmV3hWk9xp6J4WEffOfmxuWzfbs3r27mfFbw9572v3P7uycc2b+CbOwkIdSv359mjFjBpUuXdrDmlJcEBAEBAHzIJDBm6FERERQWFiYN1WljiAgCAgCpkEgzBsL0DSjl4EIAoKAIJAGBLyyANPQn1QVBAQBQcA0CIgCNM1UyEAEAUHAaAREARqNuPQnCAgCpkFAFKBppkIGIggIAkYjIArQaMSlP0FAEDANAgFVgFevXqUrV66YBgwZiCAgCKQvBAKqAL/55htat25d+kJcnlYQEARMg0BAFeCvv/5Ku3btMg0YMhBBQBBIXwi4VICvvfYa9e/f3y4qS5YsoVGjRlFsbGzK/dOnT9PQoUPp6NGjduvoFw8ePEirV6+m5cuXOy0nNwUBQUAQ8BcCLhVgUlKSw76HDRtGb731Fg0cODClDBQgrh86dMhhPdxYuXKlur9q1Sqn5eSmICAICAL+QsClArTuWLfuzpw5k3K5Y8eONHbsWNq8ebNHY9QtPxyETJ061aO6UlgQEAQEAV8g4JEC7Nu3L928eZPy58+f0nfNmjXVEnnixIkejcfa8hsxYoRHdaWwICAICAK+QMAtBQil17t3b6patSp9+OGHqfp99913aevWrbR3795U9+xdWLx4MR07dizl1oEDB+j777+3V1SuCQKCgCDgNwQyutPyzJkz6caNG3T+/Hm7xbNnz04PPfQQtW7dmmbNmmW3jPXF4cOHpyozZMgQevLJJ1NdlwuCgCAgCPgLAbcswIcffpgyZcpEc+fOdTiOTp060fHjx2n79u0Oy+AG9vxw+msrsAJjYmJsL8t7QUAQEAT8hoBbFmCuXLno33//paeeeorq1KlDVapUSTWgypUr0+uvv04TJkxIdc/6AhQgrD0IToubNWtGzZs3V++t3Wms68i/BQFBQBDwBwJuWYDoGPT33bp1o9q1a9OFCxdSjQUM0dgfvH79eqp71heKFCmi/ATxgkD56e9LlizptK7ctI8ArOd7771XsXTXq1fP4xN5+63KVUEg9BFwaQE+8MADpPsC9uzZky5dukT4wuXJk4f69etHhQoVugulcePG0Zo1a6hChQqhj54JnvD27dvUoUMHatSokfp78uRJgmvSvn37KGvWrIaPEJ+PH374geAqVa1aNercuTNlyOD276zh45UO0zkCoMQPlDD0Fl4OB6r7kOj38OHDlixZslhu3boV8OdhLwAL7xUjyVbKi5WhYePav3+/hd2yVN+FCxe2bNq0ybC+paPgREB+moP8B7BEiRJqH7VGjRpqC+LIkSMEqxAC1yRY65Bly5b5/UmxtxsfH09///038ddB/cXeMATLc4Q/+kt0SxhbARjHo48+qixhV1sy/hqPtBscCIgCDI55cjrKefPm0fjx4+mLL74g7KO2b99eKUFrBWhEzHWDBg3UOKdNm6b+Ygls78DM6cN4eRN+pfBCwCEc9pTHjBlDp06dCsg2gJePINUCgIAowACA7ususccGK3Dbtm1UtGhRWrRoEfHyz9fduGzvP//5j/Ll/OSTTyhfvnyGUp3BEuatAOWpgJBNEUHAHQREAbqDkonLIPoGfpWw+KKjo5VDOiQQLkUZM2akGTNmqKUvlOFjjz1G7733nmHowWE/c+bMBEsU3gXffvutWopPmjSJBgwYoMYBSxg8lCKCABAQBRjknwOc9jZp0oTCw8OVAvzss8+UFQh3GLgurV+/Xj2hviw14nGx9MUyFA70gwcPNqJL1UfLli1pypQpah+0adOm9Mwzz9DGjRsN6186Cj4EXLrBBN8jpa8Rw03pjz/+oA0bNlBERIRShnBWhzJs0aKFOniAMvI34w4OP3Lnzq1cccqWLatcp+bPn6+c440QWMLnzp2jhg0bKrcbHIZAAmEJG/G80oePEAjk4TU/grjBBHICfNw33E66dOmiXGHw4oOZlB4w13wi7eMe7zTHYZp3ud+gP7aELUzkYeETcHUPgr+TJ0/22zik4eBCQJbAPvohkWZIRQn98ssvFBcXp17YB9QFugdLcn9Ju3bt6KWXXkpp/sEHH1Rx6bol/MorryhXHCPcgfz1jNKu7xEIS/5V9Khl8P8hPhhSvnx56tq1K3355ZfK+x8ncNh/6tWrl8s28YGEzxaWaCKCgCAgCBiNgNd7gLZKCyFQuHbx4kUVJge3DH/+4hsNlPQnCAgCoYeAVwqwbdu2KVYbljoffPBBymYzNsJxCgnHVHcU4IoVK1LaslWqoQe3PJEgIAiYCQGvlsDWD9CjRw91wgh3B53oFEtbhGC5UoAoZy3aHrWZ4Amdsay/uJfKZC1IeSOzh85DufMkjzxC1KoV0fPPu1NayqQzBLw6BLHO+BYZGakgA20+ZMeOHVS/fv2UPUJXeGIPEIpPlJ8rpLy/v+z8Dmq55n/UYrVxPnn6aPddP0VjDs6lhNuJ3j+AtzWZe5IWLiSaM8fbFqReiCPg1RIYWeDgcAtZsGCB+gs6fFh0+vI3xHELmse7nhhHnTa8T7G3E6hvyTaGj/vLIwvp04PzqEHuClQ/Vzlj++dUDUwzThwQbGy/0lvQIOC1AoQStBbsC4oVZ755//Pc3wQlmDcyGz1fwngF+FrpTnQx4RrVyBEgsltRfub7UJpoRF4pQBONX4biAoFxh35XJV4s2Z4yhoW7KO3720Wi89C0e/v7vmFpURDwAQJe7QH6oF9pwgAEfjm1lrD/B8XXr1R7A3oMQBeJvLfYpw/R9OkB6Fy6DHYExAIM9hl0MP5z8Veo7/YvWflloBm1BoTm6S94B995h+jECaL9+4meftoBGnLZXwjs2rVLZYtE7DcOP+H/C1agYJHgGWmwIGqScSZZbtPVxFhql78WPVa4kUlG5aNhID/1s88SzZ6tNXjffdppr4+al2bcQwBBD6AeQ6ZHXZDp8X//+597DZiglChAE0yCP4ZQICoXHb//a8qWMdofzTtsc+3FPXSWrc/OBes5LJOmGx99hHyqxFz3RAUKEBP9aT5+QWR1pOn5TVT566+/Vqw7C9nVCHRsa9euTTkIhUcIskciMMLMIgrQzLOTxrFBCRopC89uo3br3qXcEVn9owA3bybm19IeKW9eoqVLiSpVMvIRpS8rBMD7OGjQIEUye//99ysOxmATOQQJthkz6Xjh6PzC3xPU6Eplye+fUcLig+M9M72wx70oP/+g7HarYODBnh/+gn0nGFMRiAJ0e7qloDMEJhxZREdunlVF4PvnFylShPhbRsRJoNTyVyTgCICMd+XKlVSE5wZBEL1796ZEnMwHiYgCDJKJMvMwEy1JNGr/LDXEVvdUpyeKNPHfcE2+p+S/Bzdny0x8q5a+EydOVCfByLdifShizlHfGZXsAZp9htwcX1xSAn3MMbeP84lvmSwF3ayV9mLo97HNH9GpuIvUJl9N+p5dbtIk7FZBixcTgcQAFp+IaRHAHmCtWrWoePHidPasZv0jKVd2hCAGiYgCDJKJcjXMzZcP0ju7Z3DYWyyNrNTNVXGf3V/MoXbzYjZRvkw5aH79QWmLNmErgvr21cZ28iTR6NE+G6c05HsE5jDJxNPsewk2KDA//fXXX9S4cWPfd+THFkUB+hFcI5tunKciza33NrXIW9XIbqkQnzQ3ZKKDviXu9075sS8Z568kzuxEzFfPeQp5V4Zz+9LAgYY+h3TmOQIlS5akNWvW2K0YLLwAogDtTl9wXuxQoI7hA6+dswytaTLSu36ZM5KPEInJI7X6hQoR/forcUiBd+1JLUHAQwREAXoImBT3IQJMocZJfLUG4df3229Edev6sANpShBwjoAoQOf4yF1/IsDJtOj4caJuvGcJJ9qoKH/2Jm0bjQAORjg6hDPWE5+MGN27W/2JAnQLJinkFwTef98vzUqjJkBgzx5tewMW/vjxxDlSTTCo1EMQP8DUmATNlZ1Xj9L5hDuB6EYM/DaTLODlliAPOfb3cNAhkj4QADMPlF1VPozjxGgEogpYgCYVUYAmnRhXw4qJv0y1Vv6XOqwf4aqoz+5D8aHPhzeOcq9NzvdCZcsSvfyye+WlVPAiwNkh6YUXiMNBiJOEE4eDaG5Mf/5JVKGCaZ9LlsCmnRrnAxu46zuVaMhIwoOb7PS8/cph1wmO8GV46SWiSZO0hwBzi0hoI/Dee0QTtFhwtZcLJcgZI80uogDNPkN2xockQ1OPLaOcEVloTJVedkr451LWjFG0oemHxDn87Hdw+TLR/PlEH36okRXkyaORlEIZioQ2AtjqQHx2ixZEb75JVL16UDyvKMCgmKY7g4yJu0QDdn6jLnQp1IBKZM5n6BPUzcVLWnuyfTsxOyYRrD8IwthAV1XO4Exw9sYm1/yPwA8/+L8PP/Qge4B+ANWfTU46ynsqLBkojJ4rfr8/u/KsbeaEU8oP/nwgLT14UJSfZwhK6QAgIBZgAEBPS5eTj2kKsHuxFuTQGktLB97WxTIXjs3Y8BZ2Zm9RNHc9HGjkzElUu7a5x+nB6MQC9ACsQBc9H3+VTsVepNZMOWXk3p9bzw2lV6WKKD+3wAqyQkxyoEhoEbbIBKjMdxVkD+B4uKIAHWNjujt5M2WnbS0+ocUNh6oDEH/L5ssHqOSSvvTF4QVaVzdvEu3c6e9upX2zIIAtDZBSNG9O9Dvnl4b1h31dk0Z1eAObKEBvUAtgnUrZ2M/KAAHJabctnyqW51UXmKMPfl3g6IOD68aNBoxAuggoAjjVrViR6IMPiG6z4ztcW2bODDmiClGAAf2UmbfzSUeW0J7rJynDbQt1XcBhTUx9RAvYEsTpbrZs5h24jCztCGzdqik6hLFlzqy5tSBmu1WrtLdtshbkEMRkE2KW4Yw68BtVOHGNfv5iN1XZdUobFvaAOAm2HHKYZZb8NA4ovVu3tHSjw4drJ/t+6irQzYoCDPQMmKz/Wxxd8szWz6jrt6vp3Zm7KWMSOz2XKaOlo2T2X1F+JpswfwwHJ/lIPh8R4Y/WTdWmKEBTTUfgB/P7mS008+RftGHDaU35gZwUWdjg3yeSfhBIB8oPkyl7gCb/SLflROPVl7/C8be8JDFAlnCOD8jqT/n0b8sWYs5zUX4G4G5YFzjQAOs2JzIPJX8+b/ETC9Bb5AyqhwxvZfkVmcGY5chLJdur/vqVak8UFm7QU0o3hiAAjr5HH73jyoStjXQuogBN/gH4vNqzho6wQrYihJdIiCGwYgVRz553UhCAuGDKlBB7SM8fR5bAnmMWGjXA3PLWW9pJX3JO19B4MHmKuxDANgZcmMDSAoJS7OlOnkx0+DBxDst0D5ZYgOnxI4Dk440aEUEJQsDbls9YVpn0CHtAnvnMGc3qQ6jiV18R9eoVkGGYtVOxAM06M/4YF6jpP/9cIy2A8oMSXLcu5Lz7/QFd0LbZnvdyjx4lunBBlJ+dSRQL0A4oIXkJfH1NmhDp7MxPPEE0bRpdDrtFHOEpEswIIDQxMpKoRg37T1GsmP3rclXcYMz2GVh9YTediOVfa1/L22/fUX4PPaTiOvfEn6WCC3sqwoM4prsXCTIEQFYwdKjG0FKnDpHs5Xo8gWIBegyZ/yrMjdlID234gDoVrEez6jKtuC8lnF1asOndpQvRs3dOluFmA2aZePYzjApnK0LE3Agk8A/VsmVEONUFOQEONqKjiR5/nCiL/xmCzA2O56MTBeg5Zn6r8cXhhXSb823cm6OU7/tANIeNwN1lR8uxtpflvVkRACMPSGdXrbozQix7oQhNnHnNrHBiXKIATTI7C89spWXn/qHcEVnpGWZ7FhEEUiEweLCm/EqU0Ja93bppeXdTFZQL7iIgCtBdpPxYDjl+H9r4Ad1iDr6xVftQ0WiJu/Uj3MHb9MiRmuJr2zZ4n8FkI/faDeYwO1I+9thj1L9/f/VIX3Ie0KG8Idu3b1/65hsta5nJntWUw7mZFK+Sm8fxHlyj3BXp6aJMOe6NgMAShKVIRL5woTctSJ1gQECUn09nyWsLsFSpUnSAv3SfffaZGtClS5eUArzIvmZ5OB9sM84dULp0aZ8ONhQbW3ZuB4F6HvJ8iTbePSI2xe+7T6sLh1eEOYkEHwLwzQQFPZiYX345+MYfhCP2ygLcyoyxX3/99V0KLjY2Vj1+7ty51d9jOJ0ScYlA5vBMqgySjt+fz4Efl7NWYmLunOoiVwMS2DjwB5twZBGV/fM/tPYiB8WLmAsBKD+4J02YQPTdd+YaWwiPxisF+DsnSOnTp49DWIoWLUo5cuRweN/6xrBhwygsLEy90qO0yFuFdrccR0dbT6R8mdzDLAWnL74gKl+e6NAhoqZNiZC2ELGedgSW5gt/T6ADN07Tzqvy42QHosBcWrSIqGNHIv7OKNcWHHCI9WfcXFi8EB4d0wTfeS1btswyYsQI1dKFCxfUPV4eu2wZ5YYMGeKynBSwg8DPP1sYaO3Vs6edAndfarN2mIVmd7ZEzX3UcinhusvyUsDPCFy7ZrE88cSdOcRcvvCCnzuV5m0R8GoPkBtJ0dA4BGnBTBNbmHUCe4Dnzp3j3DkLZP/P379hSE7UhvcMka/ViTWOYXx7fAUtZaLTvJHZ6Oc6bxiSUtPfjx/07U+cSPTDD9p+LRzTcbjRoEHQP1awPUAYNGKgBo1lL1uASnGK+AeBQzdiqPSfL6jGlzQcSq04qbqICRDAHvm4cUQvvUQksboBmxCvLMCAjVY69hiBTw/NV3UeKdRQlJ/H6PmxApTe6NF+7ECadgcBrw5B3GlYythH4GLCNXUS+/mhP+wX8PHVLZcPqhZfK80b7SLGI6BzLhrfs/ToBgKiAN0AyZdFdl07oU5iV13413WziP0EeQE4/LyU10p3ojFVelH93HxaLGIcApg7OKbjdBdO6iKmRECWwAZPS91cZWl8tecIfx3KjRva/hD7WioXl/h4on79HBZ3duPhQvbdYpzVkXtpQAAUVXBP+vhjolOcUD7ZLzYNLUpVPyIgCtCP4NprOjJDRvpPyXb2bt259uKLiqxUCdg/5mv7eM4ryd2AIzBpkhbJgaTi+tzNnUsUFRXwockA7CMgS2D7uATm6u7dRC1basovJ/M0I84aVEci5kfggQe0iBwov1q1tGgOUX6mnzexAM00RUhOBHpzRAMgV4fE9JppdpyPBRx9sPT++19i3y4mmpOvlnPAzHFXZskc86CN4sQJ7S/8w0T5mWlmXI/l55+JkGhcko27xspEJWQJbMBkHGRn5NuW2657mjWL6F8+HUZ0hxcCSv3oeY9RizVMnCliLAKI5BDlZyzmPuhNFKAPQHTWBJIclWO/v0G7Zzgrpt2rV4+oUiXX5RyUKBGdj8pkLUht8tV0UEIupwmBffvSVF0qmw8BUYB+nBMmHaBuWz9l1ggLlc1SyI89aU1Xy1GCdrQYS2+VfdjvfaWbDm6z5Q56KhxsgHknmf8y3Tx/iD+oKEA/TvCPp9bQkZtnqXqOktSreDJhKXzDPvqICP5iIuZGAPRi1Tl2unt3IubApHLlJLm4uWfM49GJAvQYMvcqYM9v0tElqvCzxdmXD5YEqOrh5vL66+Lb5x6MgSkFZde5s+aDuXOnlmZgzBiitWuZuTZrYMYkvfoFATkF9gusGgUV4nCRc7dXgSZE8BPTc3UgP6/kdvAT8mlsFpY59mIRygaBaxJO5UXxpRFYc1YXBeiHeUnk7G6D93yvWu5f6kGK+vjTO8qvWjXmpWLLUKID/IC8D5rEvNSuTQSXpN9+0/7tg2alCXMiIEtgP8wL3F5OxF6gOok5afDoxUTDh2uOsSA2mDPHZ8rvw/2/UfmlL9KGS3I66dNpXLOG6CCz6EARioQ0AmIB+mF6y2ctTPPqDaIqk36h8G9GacsnWH0O8nV4M4TLt27Q8L0/0fWkOIrnlJoiPkQgA9sFkZE+bFCaMisCogD9NDMPFmDr4aFoorM3iRMo+1T5nY2/ohKpQ/n1LHafyics4iYC2OND3uopU4jatyfipFwi6RcBUYD+nPvKlf3iN9Zl0yiV2rJYdF76pqZ3NFn+fGzTtr19O1E7ZuJBKlGI5OAw7VQZNTBRgEYh7aN+fj65hhBdAhkgLM+uUU1IIPqD2bdBKYZ43atXNd8+8CvCMhdJ1wiIAgyy6f/8sEalnzcyOz1fgrPCiThHAE7ngwZpZcDQ8s47wtbiHLF0dVdOgX0x3dOnE/3vf75oyWUbp+IuqjLDKz5JUeGyUe8aMI680eXLL++cyLusKAXSAwJiAaZ1lmFRjBhBx/JloQ+6FKYvqvdNa4tO60+s8R8+9U2k+yW9pVOcUm6+8QZRq1ZE994r6SfdQyxdlRIF6O10I1LgBc63Cxp0ljFdq1GpLPm9bc3tei3yVnW7rBRkBJB+UvLuykfBAQKiAB0A4/Tytm1ETz9NtGsXUX5Wep9+SmMef5yIE72LGIwA0k5++60Wuvbyy8LEbDD8wd6dKEBPZxB+ZAiUP3ZMqzl1qsT1eoqhr8ov5iibTp3uMOsgDaVYe75CN120I4cgnk4zWJuh/NrwCezSpaL8PMUvreWvXdMcmR9mzsOOHTXlB3++X38V5ZdWbNNhfbEAPZ30J5/UeOEMihOdemyZYpTpXJAZStK7YN8VBxpIHAXJnJkIJ7vPPUeE8DURQcBDBEQBegiYKm6Q8kNXI/f/SodunKErD8ygzOGZvBlt6NSZPfuO8oNPH1KGwgoUEQS8REAUoBfAXUy4Rp8c5ITXLIPKPULRflRML3IS9UQmU033yg9gg0dxwADtBwh8irlzezF7UkUQuIOAKEAvPg3fHl9BI/b9omp2L9qCymX1X76Pl5lPUCQZAaQK/eQTgUMQ8BkCsnHiCErEjII1BCeNVgKq+2nHl6srXQo2oDJZ+Esp4jsE/vmHaNky37UnLQkCThAQC9AROIjwABU65Nw5orx51T9h/W2/cpgKZMpJ02sPoAxh8hviCEKPr3/wAdHAgVo1i8Xj6lJBEPAUAfn22kMMdEngi4MUKZKy1wTrT1/6vsmpJ6MyRNirLdc8RQDOzNjb00kLxJfPUwSlvJcIiAK0BQ5RHjU5sfiNG0S9exPhfbKLxazT6+nAjdNUMWsR6leKyTT9IDeT4v3QqkmbRIpQZMgrXFhF01D27EQvvki0aJFJByzDCjUEZAlsO6PPP68RZnbokBLnqxeZekzb++terAVlDAu3rZnm98gjUnFZP3qp5AP0fiUOtQtlOXSIqHTpO08IS3vBAqIqVUL5qeXZTIaAKEB9QnDoASdnONlWqMDsBpwH1kYqZitCcbcTqFuRZra3fPL+owOz6XpiHF1LjPVJe6ZuJJafETjj9dJLRE2bShyvqScsNAcnClCf1/XriX7/nagQu7Rs2mQ3D+zoys/47VMQx4mNUk6XC3FoV6gL0gXs3h3qTynPZ3IERAHqE9SEk5cjrAq8cQYnwUYe4ac3jyFkemuTryY1liRHJv/ayPBCBQE5BNFnMpozuGH/r25dw+f204Pz6NfT6yhreBTNrjeQMmbw/f6i4Q+FDkEaAc5EJCMSEQRMiIBYgAGelLikhBTXmkZ5KoaOa83160SPPqrtqWbLRlSjRoCRlu4FgdQIeKUAt7FryJw5c1RrnZiPrSa7jZw+fZq++uordW3o0KGpe5IrdhFYdWGXWvpCnit+v90yQXWR45bVVgJypFzk/CU45HjggaB6BBls+kHAKwV4iF0YdCXXkdk45s6dyw78A2kqk4Nu3bqVY9Yb0+rVq4MexZj4y7TwzFZ6pFBDypoxyi/P0zB3BXqicGMOqStIDxeq75c+DGv0yBGirl2JcKAEAUv2Dz8Y1r10JAh4ioBXCrBLly6qn4v8C18l2W+rVKlS6lrFihVpzZo1ShHeiwMFMwoC6r/7jmjiRKI6dRyOsNP692nj5f1k4f96FrvPYbm03IBinVn7tbQ0YY66339P1LMnEfLwlimjRXU88YQ5xiaj8DkCFg5V3LFjBztO/E5JSUnUunVrqlevns/78XeDXinAhQsXUrt27dTYYA1Cbt26pf5G82FCo0aN6MqVK+q96QTWCaIPsFQDu7ATmcGxvkhCDgtQxAUCiOqA8sNeHyI58uVzUUFuBzMCi3iOdR2A5/iA47ivY9832IQ1eZrkhRdeUPWHDRum/t68eRNR7JYDBw64bBflrF8uK6SlwO3bFsu4cRZL9uwWS0SExTJypMWSmJiWFqWuNQK3blksJ09aLElJgks6QKBv376WGjVqqO87Gz8WVohB+dReucFMmDAhRc9nyqSxFOuW4MqVK+mVV17hKCerMCcnvwpDhgwhRk69/CqwShBxoEd8vPUWUXiIuJv4FTg3GwdDM5zIhZreTcCCu9g999zD3k3bOS3OUsrIc3///cF5gOeVAtzNHvxhnAISr6pVtTy1T/B+D94/x/kZxtgJIwv4dGO/TxfkkBARBAQBrxHA9zxHjhzUgWPmH+FsfDFgUEqW999/X/0L5wADwPJjYvFKAY4dOzbFauvVq5d6vLZMUQ4r7pieLtJMDw3lxyfVal8KeSQaBm5PL+F2Ir28YxK9u/cnMyHk3lj++EPLwSFsLe7hFcKlihYtSufPn1eHILk5NUH9+vVp//79QffEXinAoHtK+KNlyUJ8PE0U4JNJcArOPPEX/R6zObhgBF0VGHLmzdNipYNr9DJaPyCApW/79u3ZmWIiFeB0Bdj+Cjbx6hQ42B6SsN+HMLecOZ0O/cjNs9R/x2R6nP3ynizCscF+kKjwSNrRgpVJsAhOd199lejHH4ly5SJ6+WVtLzVYxi/j9AsC3bt3V0vgPHny0IULF+gI+4A2QTw9y7Vk7wrsEZpd0ocCxCy4UH4o0nPbOFpxfieVypLfbwoQ/RSIYkUSDPL55xpTM/LxQn7iZTvy8oqkewRSLy9mAAAgAElEQVSwB9ijRw86ePAg89kWpvnz51P58uUVLmXLllXnAc888wz/Zpr7sx6Gs+tAzSZAwimwGULnTsVdpMKLelMGCqO9rcaryIx0LStWELVooUGABOS//oqN3nQNiTx86CGQfixAF3P3/YlVqkT7/LVE+QEIJILCoVG5cvByJfZud4Gg3BYE7iBwPdFCO68m0a7rt2nPNX5dT6IzcRY6cvM2NcgdzqxHvCdvAglNBQiPdA85/XAwAenqp70/E8y1Z0MAkwteIoKAmwhsv5JE6y8l0Y8nE3grKclhrRo5zON/G1oKEC44zE5DyC2L2FQE47shs09vUKkuC0XlVhagrwWECjj8aJ5X8l34Gltpz3gE4pIs9A9bd/9cvU07+O+/bOHtYOV3NuHObloU+5dUzJaBKmQNpwrJf4tEh1HZLBnonkzmcT4JLQUIkgP95Cl/frc/GTj8uM1ReeOrPUc5I3xrmp9PuEoPbfyAc4ncIkun39wekxQUBMyEQEy8hb49lkAzT95iY8G+dVeGlVvjPBmpa+EIuj9fcKiW4BilO5+EZcuIJk/WEusMH07UzP3ERa+X6Uxn469QxwKOmWHcGYJtmVhOcdlpw0il/F4oYcIDhF9+Ifr4Y23Y+DfSU4qkawRusxF3iPfptlxOok38wp7d36zwDtxg8pBkiYR1lzUDYSlbOVs4VeW/1bJn4BWUeSw7dycxNBQgwnDatCGCu8bo0UT//a+7z6/KvV3uEY/Ku1v49zNbaO3FPVQkKg99Ub2vu9X8Xw5MOEhCjsMNCOJ4k2O6/d+59GBGBE7F3aZvj9+iyUcT7lJ2+lizZgyjp4pEUI9ikVQ7ZzinhTXjU3g+ptBQgPBPg/IrUcJj5ec5ZO7XWHiWk6qz3HdPNfcrGVHys8/uKD/k40V4YN68RvQsfZgIgZu8lzfrVCItOneLZp+6RXxQe5fAoGueNyM9w0rvkUIRIaP0rB8yNBSgTr4wbJhpPl6bLx+gn06u4Q9NBnqxpMadGNDBwd2TmTuYtltzaAZrCwLV332XCH5+IiGPwCFexm7kZe3GS4lqibuNl7bXkn3cI9miw5K2Flt3sPDq8Ks6vzfC0kMM8VscrQVnapCrPsApFPSUG/6elNBQgHFxRE8/TcThOWYQEB60WzdcJTh/p9yjVCdX2cAP6y9282HWXiXZs2s5kDl1gUhoIwBfvK+OJNDCs4mplrZQbrDw2vCBRY+iERyhFJg9vM854ggs8sgrlJl/jAcPHpwyKWCWefvtt/02SaGhAJFg241QN7+haNNwAh96lMh8D/+alqYhFdxzxfH72LDExcEQ/nL+Fqrle3cfvz+DdOAUgYvshrKZLTs4HW9gf7z1F5PoMB9i6M4p+TOFpVh3dXJpll4+k7ikZOPMgWCXKceO96Oxj2+QhIYC9FD5wTXl80N/UL9S7SlvJFtDPpasGaNpU7OPfNxqGpurVIkI4W0iIYfA2ouJNOZgAs2NuUUJdw5r1XMWigqjXryHd989Gakpu6hkMOHhxX/50HLatGkqlhj5hmARgl3GCAkNBeghUr+cWkfD9v5IRaPzUu/irTysLcUFgcAhcPWWbuXd5nw1ibSGrbxjsZrWi+YVbEMOMyvN/ngNcmVUIWeV2Ak50oxazwpCnVtw8eLFNHv2bMUtuGTJEkWq4G9Jlwqwe9Hm7KFemD8sFfyNr/Ht79xJhD3R2rWN71t69BsC8MP7+EA8fX/iFl3lOFtrgQPyiyUjqXvRSMqN04wgFJ1bEPyCUIDgFhQF6KeJzByeKTTD0uAOpIf/MU0RJacq9ROM0qwBCMARecQ+KL4EumnjplKFrbvXymSixzjyInO4eRUflPc0jiL581yisk6n17rb6+CNN96g3r17qyXw3r17CSk3QLFlhASfBbh2LdG33xJ17iz0TPonBFTk2DiePl27gnzM4tpixPfH530cY4W3kpe2y88n0m6OsYWrSjyvcHFWUZddUxrlCVfhZpU4EqMsv8KZUs5MEsMO1crFhuOEt/HfrTx+PJO+NXnOKl5YHzeIVRs0aECXLl0iHIZwpkmOa+DABgMk+PgAW7YkWr5cI+bkfQIzCELdBjCT9OjKPQiJzg2VzUytjxzNfIKmlB5vJnOWGkOHIJ2lHYE9TBs18N9Ymh2T7JiX3GR29lXpVTySBpSKpGKZA+Om4urpYKVOYFcbuNtc5j1KW8kZEUadC0ZQM1be+Iv3ZpHgsgA5ITvBnw0nRAYelbuarH+uHKFvji2l1vlq0MMF67sq7rv78JdCBi5YAVCCiIEW9xbf4evHlmAV/clW3lJeFi7jF8gGIEyeonzzWvCpbSWOs23A7io5TKIwECcMZYdYYbjb4LWVX3C10QWuhHCghjM1HKu1eOEMFG3SJXrwKMCEBCbr66qFvH35Jbut1/Djx9Ozpuuyo/O5ttMoe4TBERU//ECEuN6RI0nlPRExPQJQGEP2xtEfbOlZe6wg1nZI+Uz0SulMhkRfeAIUTp5/4lC5cYcSFA2WrcCie4YdqREnbCauP9tx2nsfPAqQc4zS5cvEOfiIHnzQ3rM4vfbnub8pkTOytc1X02k5b28arvwwUCR6xw8DkhaJmBYBWE7L2NqbdjyBwyPv9tWrwPt4g8pF0SN8kBGgQAyHuMHCm8++hVja6haqXhhRJNiLfKFEpDqECVYJHgU4Y4aGMaxAsJd4IKC6emzTaA5Ni6OTbSZTvkw5PKht4qLI0CZiSgRgNS3mpS1OPvE6mEwnlZmXuI14idual7itOQStOtNIRZjATy+RtTT2IdeyX+Fqdqz+64JGhQVwsfNYivcf67NfYT1ekpfjdXqtHOYiNvX2Q+CZJvG2F1/UA8MzBDG/HsqQPTPp0q0bvAFbL3SUn4cYSHFjEDjPp5xD98TR+MNsmVtJEfZSBqPKm2UiAxZza4sA3AnhTL2CrdMp7KZyLPbuA4y87FPYNn9GPoDJRPfynl4oSvAoQLh2wDPcQwff47Hn1QFFdIZIPqV9Jrjm8MQJonHjtEOO997z2PINrocNztGe4iiMVWw1/Xn2FruuaFYT9vZgNcFlpdU9EWztwXIKbBianqRoezKN/T/snrKL3WwuWp3aFuGwOVh4DXlp24xfNfkQwwTGqV8/GMGjAL10eZkXs4njIxP5Q1jdZ9nelp3bwR+MMP85U+Ngg9OFKsJS8BxGsWsNDjk8jHn26ycnnTe+mckGRuyPV3tkNoEZ9BK7rPyvfBTHmQfW3QP7dlPZsoMTMpa39qQEL21x6tyXXW2wxE1vEjwK0MuZmRfDfnIsHQvU9bKFu6utv7SXc3yMVEr1TLuplD2jj09+Ecr25ptEf/yhdcyhQTRihCg/n8yed40kMZfiv2w5aQ7KSeygnET7WKFApcBtpQ5bd/exlXcfKxK4rmQPgNvKCbZE17Eluo65/rCUtaWxh0WKuODK2TXXFESRVON/m9W30LuZ8rxWSCvAy7zv9+e57QoV7P+lVa7zIQp4/q4yz9+Q8o/7XvkhL4eeihIHPXBv8ZDeP63PKPXvIID9vIVnEmnU/jjayctFa8nNSu4/HH+LGNxA8egl8MHFHzy+MQfjaRUfWtgKTpUf5xNancYerjYidyMQ0goQCguuL7VzlqEi0XnSPPcLz25lT/cbvLTJRm+V65Lm9lI18Prr2iVw9mHJbyJfx1RjDeELWDp+sE87yLBd3oJ44AlWKoFUfLD25rPiG8uKz3ZpCyXXPG845+8IXRp7X370QloBQuktbzRcKcC0SqIliT7cP1s18xpnkYvK4AffJ5AXcEwkU+Jy2q2KaR2y1HcTAVh6K/kkdA27f6zkgwzEr+oCPr0mfCCAfTKEclXkJa7RgvhauKX8leyeYp2WsgCTnIL2Cj55iBrBclwMPfdnyNwK8OJFzfHZ/edJVdJXycgH7/6e0wTuVwSqL5d6IFU/PrmAnB0ihiAAy24SZ0ADxZR1ykd0DgXSlx183yqbiVcOgYm/1V1URvP4sMy1FowPCvl1ZoIJlvy7hkyqF52YUwEigU9fTiP5889EYDoJcMayvddOsvX3m0qavqThUKYeyuQF1FIlkAjAMRkWHg4KYElt5FNcnV5KOSfnzqisqMZsTYFUNMrg2FWkpQSF/XpQ2fNBxib+y5eUYHz12bqDJYoXLD4z018Fcp497ducCpA5wejrr/mILaspTj8LRuWiUlkKcHrAFhzrWNJTjO8uf/asZtV6GM2Stk7Tb23w6I0+kEDWy0YdjY4FNCsKii8QAt+8zzi+dtyh+FShZhgP9hv7s0vN8yXNFx8cCLz80WdgZt7Vk8ybp5UAw4kJFAXifPe3+sLVqJ3f37iRCOQFUOzw5ztyhCjc+P0k54MM7rtgKoFlh4OBdWzlIaxLZ0/GshGJgBqzpdeILShYUkazJ4MBBhYecnhgbOD60w9Z4E5TN5nGHtZefR5noP0Ig/vT4N7ozakAFyzQRu8F6YF7j21wqYkTtSU9ukU+XkR3iPLzySRAgcDZdyxbUkgBaStYzmKvrBXH3gbKDeRTPq0FqzMOW2ylK58ov8rjA32UiPEImFMB/vuvhoQXbiDrL+2j1muHMMPGo7yJ/bDxiNr2yMmeVQJyXZCSskcP21Ly3kMEdBJOxNxiKWkrD3IM65t8iNGQLalAhXPNYgqp1/6NUxx61gL/PByy/JcVX6AOWWzxSq/vzacAQXePfTLE/Fau7PG8nI27zKkAc9O1W7Ee1/V5hT59iCZPJoqM1LgMQeTQtq3Puwn1BuH3Bpr1TckknPi3tTWFcC7EsGLpWDeZrSQQy0ecJoMvb+GZW7To7J1sbUWjw5QFWoHXubBIMUazZ2oL9c+U/nzmU4BTpmhjQxSEF8vEjgXrEl4BFxAZQPlBxo8ngjIUcRsBKD3QSMHCAy+drcCKeoqzoL3ChwRVOKQrkALFN2BHrHJOtpZyfIgxrCJz/TELjPjmBXKGHPdtPgWI5WKrVkTI/REgmXVqPU08upi+rzWAN8qzeTeKIkWIwGFYgVNvgslGxCECF3lvbM91jWIdhxiw8KwjHMA4fC8zk9TifTLslYGaCVZfoJRKXJJFOSYvZedpKGmMFwJ3FcTXtmGeP/jnYaxi6TmcdlPcMJ8C7NiRmQv4FUA5dDOG1lzYzXtHaXSCffLJAD6F+buGknuX6eFncq5bW4GFB2ff/kwR35aViRkEe3rj2CIFh571tiMU8aBymegdZoAJlFI2Az7BOAavPlkHDhzgDIzT1fN26tSJatasSadPn6avvvpKXRs6dGgwYpEy5v9yqFuPoi2V47OI7xCAG8gqVh6r2QUEoWe6lQelAZ837OPBaoILCHJLBFKZgMF5Azskg/UFrisb+GWd8awqMzlDQd/Pe3st+SWOyb77nBjZklcK8O+//05Rcv369aPPP/+cBvLp5tSpU2kr5+5o3LgxrV692sjn8HlfeTNld69N+PbFxcnJrhO0kAfjzV2pT0PhlvJaae00NFAuKtbDhoKbyPkvvuSX7cktykE5gwShbf4IQgyuSPAj4JUC7NLlDhNKoUKFFArlypVTf0uUKEFr1qyhgwcPUunSpYMfIWdPsJ2ptp59luj6dSLw9uXL56x0uru3mFmS39wVnyoKAye08M17mZe3gU4EhKXsenZMRl7bH1lR2/Go4VSnEYrktCk7TwfKpSbdfXgMemCvFKA+totMVpCUpG0Ax8Zqbie5OWtb0aJF6dixY24pwBUrVqRYk94unbdePkQ9t31GPYvdx2kFO/gfunPnNNJSHHLg+TmTvcpWl44F4dsHeYmLkLMlrPj+PKfli4WHXkG2lrBcrMbL2hZM1VQnZ2AUCcZ4lE+XsZxFpMhGPrzAAUZCspsednyr8dIWjCqw9uryC0vzQBCcpuOPkqGPniYFmCdPHjp06FCqAR8/fpyKFSuW6rq9CytXrqS/+dUZN0H+ifhfD+WXU2vZ/+ooJ2w+42FNL4t360a0aJFWGezNoK5PxwI3kP7sBmLLWgLlMYQPBh4rnDGgp6Hg94NvHvLaWlNd6VOGccIx+Xl+mWEpno4/SoY/ulcKEFbbJ598Qlu2bKGSJTVygJs3b6rB79ixg+rXr0+5cuVy62GGcE7bobNmabGxEyZ4xYC8hHP+QlrmrepWn7aFZp1ez8ugvfRexaf4i+oEkjOsYKH8QFYKBY+8vOkwNSWYVVbwYQaSfC88m6gsKkh23tODBQU3EDj+wl3FaDcQLGGxf7eGx7cuOe52B9PZ6wKXGt1pWo+5xTWR9ImAk2+7Y0Cg/OYxYQFeEAuvLVq3bk1hnChIX/46rm1zZ+1aTfnhsptWo3ULR26eZUfZA+qSNwpw4dlt1GXjKM7iFUbvV3KRchOn3LryA2MNkhWlI0HI2efsBgIOPetIDOzjDWZL7w0OPQvUyS2svE94XDjAsA2Nw5jA+AJmlc68nyciCOgIeKUA586dmwrBthziBUXoqWRAEiBdqlXztDpNP7FS1WnFWd/A2uKJ3Ga6/Jf+YXYWFtBcZQxzEVGAbG2Q/v3TlfLj1BMqyffrO2NT5cboWSySPqwcuAxoiBh5d288fc3kprYCyw5KDzG3srS1RUfeAwGvFKAvoauHE1RI8+ZE5ct71PR1Tk409uA8CmeH5ZEVXVhvdlqednw5swGfVndeLeOG8zVydnTm3UovFLWd7k196TxbVIvP3VLL3Hkc4gV/OAj2y9ox0QCckxGdYXRCoIM32IeQozDA/GJNX68OMHg8oLoqlzWDIkHA+OTU1tQfs4APLqAKEAvIFjoEw4drCcA9gGQt79udT7imrLfaucp4UFMr+ikrTwjqdy3cxHX9LOwY7QVDjeuGzVMCvnCjON/t50zSydFpKQK/t3HVolVcayAELjXD92lRGNb9Y3kL3zxEYQSCACEQWEifvkMgoApwED8H86QQPfQQb9I09vipikbnZbeKqu4pL6vWsVQfvGemOjmulr04zak7MO1hbx6P3jwVsGeGQP65p8FikkgXWQkipzfo4RF/26FABONsnOtKPMfagix0F1udy3npjZSPx3ipC0E6ykacnAj5d5vz36Y8LonCMM9nKdhGEsbKwPONOx895RE+NCmBtpD3o4znFpy3w8DBScklfVVmt8P3T2SvfmZoToeC0DREaPzCMa7WDsBY3o7mfT2jWVZAMjD1+C0ayeShusLTpwVLb/D7PVkkQhReOvys+uuRA2oBPsVPNZjdStoaqPwAJPL6vlCiLVVl68+u8ktkWqMRI4jy5yd6/nl/YR+Qds/G36bZpxNpdswtWsXxuLylpgROv534hLQD58moaiC91D9s6eGABQ7US/kvTnPhlFKK2V4qs0tNMz69hfWJ2NsI2dALyGcmlDsNqAJkBxhaz7lwjaYIzZoxmr6ozlnnHAkiOyZNIipQIGQU4K5rSeysHKfom3SJ5JODfrx/Bidgo629Fax8X2e2ZFuuP/jmjWLrE2FnIoKAvxGQT5ktwojvhfKDDBliezfo3mNZCd895KSwZjNBqNfYqlHqtNRIwWnyoN1xbIXevezGIcvHVaLVEldEEDAKAWM//UY9lbf9YOkLVxfIU7xAD9LlL/z2YOnNYiUzn5e6J+O0Qw0sJUHH/nBB/DVm6qGAQRyKw5Vt7FIDWntehROyoDViK6+9cqmJUO41ssL19oMr9bxFwJhvgbejM7oelN+ff2qpOD/6yOje09wflA1YTZAhzZrOCcvKr2pEK7ZiowRJvT/aH6csTz3BN/oGa/IrzALzZplIw30IjXp26Sd4EAg6BfjXhV3UccP7VIxdYNY3HUXR4ZncQjs+6RZlCneyvEJ0y6efaqwuv/+u7f+51XLgCyHPLE5yf+PDDV3xwaLqwj57Rll7OFwB0elOjrtdef6W+rfOslKTHZJBEQ+S0/uYDeaeTGlk2g485DKCEEEg6BRg8eh7+BQ3Oy/hyrmt/BDtUX35AFra6F3OHKbxFqaav8WLtUsIc2Myh2AQZCDrvS32roOEChwFARr5PsUjDYnLRUTGKI7BBemprvB07DrzifLIytGcDU0UXjB8ntLjGINOARbLfA/tb/WFR3OVcDuRKmcrSom3rUIbbFt45RUtedGjj9reMdX7/Rye8fMpOAfzi/fW4B9cKCpMOSs/xhYf6Nn9Jdhb3Mf9r2DHZJzi/svKbzcfavDKm6JZxzVlx+SKyQ7K4P8zOkzOX88t7YYuAv77tpgIs0qs/DY2G+18RPBFNNgf0fmA7r6LzGnDeT8NIWq60zJYWN7hZDxwEPZnsD/6w2EK9vNs3VYQmfEfdqVBOJooPE9mVMqaAYF0oQDNAHRaxgAn4We23uTQvTu8dtjjm1IzWtE8+Uug+GDpDdkTR2t5T89a0P8ThSNE8fkLfGnXEAT89+0xZPih2QmCE//m5SWUzswTTACQrHywlwYygq7sK1eB/Uj84TYCdmewJ4PdeSUvs28m6z2QnYLOHktsLTLDuBPl0JxleSozICAK0AyzYDUGOCv32nZTnejqgqXu+OrR1Iu59/wliBRBXPAfMYl0x84kKsKbe4N5mf0cR4uICAKhhkDQKMAlZ7dT+ayFCYcgaZYff9Ryerz3Hp8gaFnt0txmGhqIYUc55J79nhOEz+O9NvjNwVG4AUdpYJn5GL98vceXwCcaS9g5eQEclHmJvZn7521GzoUcxvG34fQAH6q0YWuvGMfkiggCoYpAUCjAE7EXqO26d5n6qDItb8S8gW7I27umc9rFB1OTHZw4QdSnj5bK8umnA64A398Xx6Fh8Xc9Ue9iEfR59cx+SxmJ3LdIYmTtoIwl7qt8kIF0lbnBhSUiCKQDBIJCAU46uoSXZRa2TpiQ1A1B+ZH7f2UXkQQaU6XXnRoIdYObC1ioQXRQt64brfmnCJacz2y924evGC83EZ/rj7wVONCYfjyBvmLlB2tTFxCKor/hFaKoQjax9vwz29KqWREwvQLcc+0EjTk4lwk6M/KXtKtLHBfzUnnAjm9U+YcK1LtTPiaGqFMnoo0biRMWEy1b5lUKTpcDcFIAoWq/cnzuTF7qLuNYXfjwFWEfvof4YAOkBO05WsKXOWjht7ecT3F/4z4X8KHGIeb/g4B4AEtc9NeWY3GFUNTJpMmtkEbA9ApwwM5v6Crn/micuyJTNhV3OhnXE+Ooy6ZRTOUeRw/kr62WzCny/vua8sMF7P15kYHOaedObiKN5BBO3DOJE/foGctwsDGkfCa/JeyB394L/8QRkgbpUoL38+CvB789UXpOJkxupRsETK0Ad107znlnt6nJ6FCgjstJmXz0T1Ywcarc8yXa3Cn/008axVUkn2QOHKgtg122lvYCq9mNZDpbe6CaP81EnxCwsXTlQ42Hednp6wOGdRwTPJND0tZwpAZ8B6H6SrLS68zsL53Y4mvG0Rki7iNw+PBhmjZtGvXt25cKFiyYUlG/jgtP8z5yGRcO9N988w3d5oyCfbD37KYsXLiQ1q9fn1LadgxuNuO0GHJ4Dxo0iO699163niM2NpZGjRql2ixSpIjD5zlw4ABNnz6d3nzzTYqOjqZLly7R2LFjU8ZSjI2PXr2stqacjtK/N039jZgfsznl6R8sUNslEhOOLFRlGuepSHeV/5pTX/LkcSJjogcfdNlOWgvAl+7Z7bHKiViXBzku9jWO0UWImK/lEPfX26Y/LHOHV4yiHuw6E6hcvb5+TiPbgwJq166d6rJjx44pCnASc0U+++yzdOHCBcqdO7ffhrRo0SLV9pgxY/zWx6ZNm2jAgAHUokVKajKnfUH56Ypv6NChqq698ZUtW1a18/LLLysFePnyZRo2bJhXaXOdDsgHN33/bfTBoPQmtl85rP7ZqUBdqpi1iNOWvz+xivZcP8nJcorSjHsH3F0Wbi/79vmV5OA0H6n+yNYXDhh+5+UnMqoVi+b9Pbb0uhWNVMmFfCnY34PLDCw+vT/sJ4LWviEnM2rHHHu5Anyae5yX399xjg+43Bgh+HHx9Afm4sWL9Nlnn6nhbd26lb766iul7OLi4pSSg/LTBZYMlN+hQ4e8Vn4TJkxgmsk7aRZmzpxJe/fuvQseWE6O5PTp02qMkHPnztFwzqbojSLGc3/77bdUokQJWrlyZYq1hnZhsR47dixlCDly5FDKDnWg+CDdu3fnrfTS9D5vLUHJ6YIfjj+ZUq5Vq1Yp18z8D1MrwHcrdqWHC9Xn6IeGLjEsxiwx+SJz0O/130ntK4hfaj8xvOB0FfG5w3mPD9nUINjfA+fd8Aq+j9HV+/v4YELK/p4/+3MJvJMC+EEA+7OR4okCxBc6T548fB62jPAlh5WC5SC+5J2R/9lGsPRt1KgRdeM8NmvWrFF3vbEEG3MGRCgYvLp2dXyw9ynTs+EF0XOXYSk8F9RtLFhKRvK2jj0rTBVwIlCazZs3p2bNmikLEIoLVufBgwdT2retHoODxGTJmVNLJIZlsbUCbNu2rVKU9iSMk6BBgLe7Vqe9dnx5zdR+D2WyFHRL+QEQLHvPtJtKJTLn8yU+TtuCH90Tm27QgJ1xKcoPjsS/1c3M7jdRPndePs+eyg+u1/rTDzf82Z/Th3fjJixRXztwu9Gt20WOHDmiFBq+jFAqUDK45kyg+LAviLKvMIOQbj06q2N9D/t6qA8lu3z5cofVoNTQB14YI6wyCJQeBHXffvvtFAXpsCEPbmBJrCtXD6q5LFqyZMmUZ9myZQu1bNnSoZJ02ZiPC5jaAvTxs/qkObiy/MCWzdRjCYreHbGyiNp4ipe5PYpG0L281I30YZDuDTb5lrDLDKJE4M4CCxAMLE04WgNRIvDhiwo3p+MyXHuuPZDdJ7j7o5EbN25wIFAh9WXUl5HZszseb65cudQw9L+wBKHMPJH6vBLB0vHKlStqyQ2ryt4S2NqqQh+6ok1ISFD1oCB169CT/p2VxXIa4mgJXAC+s8mCfT2I9ThTbmWWigYAABt9SURBVDr5ByxsKHT80HizdHfStFe3RAF6ABtIArpuib0rudBTTEwwqabvozag6JA4aCDH5+JQRZcBpSPpE04eJJJ2BCpXrkw///yzemFfD/tcNWrUcNgwLBnIrFmz1AkoNvnfeecdh+Xt3YAFiD3A7Zx8C4rQ3lIQCrl169a0evVq1cQzzzyT0g8UZq1atZRFBSvyaxzw+VgcndBiCQvLE2PG/iH6hgLEkh51HNWDQsVSG88L5Q0rGorQDBLQxOgAdAhnXtM3Vn0CCB+/0+zZRD17Ej3wQJqbtLb41jArCxRTjRwZ6Bm2+LDfVJ3zbCRvbaS5L9DZI5kRnJYXnr2lrEvYdsiJC2uva5FIXuKbetcizRgY3cBHnPtl586d6jDA2j1jwYIFtGHDhpThwHLT97d0a0y/5mrM27ZtUwoLX/pdu3bRT+yW5cyNBO1ZW2HW/VhfL1++vNM9RFfjWrFiBRUvXpyg2OG6Eh4erv7tSKzdWaz7xphq1qypXlBw1stoKO+oqKiUgxu07dPvu6PBunk9tBQgf7iIf9WVsH+Tcnj2UnBy+T4TgCLBkJ5OEkvPj3lvrzsrP1+tcqFQf+Dl7Y+nElIxsUDZfcksMG05YkNEEBAEfI+A6b5Z3xxdSkdjz9IwF2FvcUkJ9N6+n3kPrB7VzllGQyb5xIyyZiV68kmv0ILrxgxWSN/yHh/o3iGw+HqyP92jHLJWEEeuaRSwvyxmSw/W3lJ+neK0lZDsPBtIFQkWFoSqgXRURBAQBPyHgOkU4JhDc+ls/BWXCjAm/jJTtP9CZ7hs7RqsALEp+913GlLYzK1UyWPUcLjx4t+xKSe6UECDmAvPVxYfwuD67YijaaxcrQWW3tO8lziAXWeEicXjaZMKgoDXCJhOAf5c5w1OrXjU5QPB3WVg2S6K8krJiBHE3qtaXo9+/VzWty3wDvurIeeFLj2Zkmpijcw+iaI4xRYf/AQRFqfHAqOfvOyoPIx9Bf9T0r3UnrZjlveCgCCQNgRMpwArMOkpXu7I+5WYzw/CJ2oqpy+Wvr/9piU2d6MBhJB9xk7Mi5gUdA8vdyN5xdmNLTEoJOSyTcvhBoIfFvNBxrccCQHSUX0fsTq325HD4u7nZS7cRHy1l+jG40oRQUAQsEHAdArQqxmCZzy4/rp0IapSxa0mEKf76KabBOdiSF3235tTP4uiikqr4DT3oY03FSEBBLG4iMnty7Ty9ZkMQUQQEATMgUBoKEAEc7MfF73+uktUYfVhuYsYWj7U5TjjjMqZ+HF2M4lOg0NxErs5LD+fxMmEbjHx6C06x4oVscBwXenODtKVOF+uiCAgCJgLgdBQgE2aEOHlQt7jPb5hnOIRrieQqfdmpid5yesLAbszTo91eZqV3viq0T4lOPXFOKUNQUAQuINAaChAN2b0Gz55HZwcmA9/vl85XteTwHlHXcCi7MJLaX25i3I42Phf+ShHVeS6ICAImASBgCvACwnXqN8/X3M8awQNLf84B8/bD/PawSfDr+2cQr2Lt+LlamO34bvES9Ehe+NoEufCgDTlGFqEkqWFnupM/G2VtnI9E5DO4TSSOOAomTlMpa18kP33avBBh4ggIAiYH4GAK8BZp9fTqcO8f8fydJFmrDzsh+KA7XnJub+pWo4SHinAF/6JVTx9OOH9uU5mlVjcW9GpqIaxS4t+qgtX5T7FmZLID+wv3o5T6gkCgoB7CARcAZ4qokVbVMlWzCHpKWjuZ51ap57orkRHTp4RER0vsFPzHxxXC3+7qTWjVXSFN/IPn+Z+z0r0F34d5BNe8Iy24Dhg0D3h8KQqxwOLCAKCQPAhEFgFmJ1zdNTU+PvGVO1FmXgZbE8+OjCbjsddYBeSchwqVlEr8sEHWmIjByFvj/G+HNiZwZK8qXk2r9xbwMIyjJfP3/Oprs7HguiQ72plFncWexMl1wSBIEPAKwUIpox///2XvU5eT2HE/fLLL+nMmTMEyu569eo5pMa5C59nqxGFZ6CnijSlVvdUtwvd2ot7aDQrwOgMkTSl5ktambfeIs7OQtxRqpjfhex0jJNeKL9KnOd2KlNVeeLbl8gezMvYneVrzuA265Sm+PKwyfcgp4/EifH9TDUvIggIAqGBQJrYYEBnpVOCIzcAGGp1mnHQ64D/y5mEzXmInYQz0Ll239pNen7bcpvKL+3HfHinVVa4ufXeJjp1iqhwcqQI/P4+/DClCyi/dutuqPdQfn+3yOZxKFv3LTfpOyt3FjCxTOHlcwEfkCA4w0LuCQKCgPEI+IxuBLkBIDrLq3VSFWePhUOPnBFZ7BY5cCNGKT9Iw9wVtDLJJJHaxTu5QnBAMcQq/8RgdkPxJBsa4nUbrLqeovxAULC8URZa0ICjQ0T52Z0fuSgIBDsCXi2BXT100aJFVZIZl3LjFm2ePJvCmn+siuqJX/R6uVgxIsE55GleJitJTgjDDJbEqafUpa1MTd9t603ade22svyg/B5387QXYWs/8eHG+MPxdCxWc2dBLDDo7fNm8tnvgzZ2+b8gIAiYCgGfKUA9NwCWwMePH3dPAT71u8YIPXeoXVDuyZSD5tdnYlNdEO+L3L6Q0aMV+QHYVRB3e4xPfRHPu6ZpVrctP9Bfdd18M6V5LHdn8AGHUFLdgVz+JQiEMgJeKUBrunAkS8YL6flAdY1cpbjvav/PK1DffZfo6lWN6v7hh1XODCQgv8DOzu34kOKLatFuKb+dV5MU2/Msrg+pwlYjeP+e4LhdEUHA1wjM5hQN9tJs+rofT9uzzjHcv3//lGRPnrYT1OV52RkwYeAsnBPE/f6feMJiyZrVYjl92jLzRIIl45zLFpp92fLU5htutzHv9C1L9vlXVD38xXsRQcAWAU7fiIhxC+ewvesWJwJS1/HCv90RzovhTrFUZTh7WqrvB+cHSemfDyBT1fHkAr57fFjpdhUdEzy7s2dCuxi7LmwQpYzZE9zcHlgaCgbXJhenB9y1Zhu1PJhNLV0R3QHLDZafK4G1WHPFdeqw4QbFcmpL0NuvapyFQ9e8MoJddSf3gwwBeC0g8TkEiX2QJN1Wxo0bRzt27EjJcYvMcJ4Iko8jsZArWbt2LTVo0IDKlClzV9GOHTvSm2++qfpHfl3kJbYVJChylJjctiwsQE9WahMmTFBeH+gfyZTw3lZ69Oih8LMVjBX18PIUN9u2fPk+qBRgjCWC2sXkZ9op3gtkGctsK+9VjHLKuILkRlgmW/PzTagRTT9xWBzISUXSLwJQeHDlwgvJuvWMaMjeNmfOnFTAIH/v2LFjU11398KiRYs4c4OWTxd1kIZT71//i+sNGzakdevWqXSYukCpzeP976ZNtcNAjDFPnjzqNhSOXh8K2p18u5MmTaKJEyeqekhrad2P7ZigeCHISay33alTJ5qODIw2MnXqVFNlfbMdn+37oFGAIC5t8td1ddgBQfwtyAdcydu742kSOzVDcjILDHz63Knnql257wYCmzcTFSzIuT05dtD2lYVdn/QkVvaa+uEHx3Xvucd5XXvt2bkGKw+WH6ySwuxbaq0I7BSniIiIuxSWvTKurmGvDQpGT26uW0X6X0f1kUjdkWDvHfUnT56skqVDsboSWGFQsKiH/MNoA/WAie2YkOby4MGDrpp0eh/jslbyTgsbeNOU679XmfXl6yOLaVOz0VQhWxHl5gIrDqFp1ThH7nhe8jbm7GnOZNWFREV/9deFJLVURsKht8tmcmotOmtP7nmBwL59ROfP268Iv1FYWXaWcarC/PmO67I15LSu/R5TXc2ePbtaAiI38ODBgzmN9ANq+ejIgjp69KhSDhDeG1R5hN31d9U7x1IQVhKWj2fPniUkSrcWRzlzkVvXkRQoUEDdOnnypFoaI3H6mDFjHBV3eL1bt25UsWLFVBYccgC3adPGYT1XN5BPWccNy3vgBmta9xxxVd+f951rEX/27KRtECM05pjfItH30ICdcfTpQS1ZEULa4JhcyIVj8ueHE2jAjlhFfIpY4OWNs0qKSSd4++0W4rQdxGq77BPLKztLLJf1PCiARODLly9XiqNXr14uaybCDStZcubMqdy9PBUss6Fg4TUBxYCXO1IQljQLLEFdQetWGdrCkhYK3Jml6KofLKshjpRwVuTcSZbtnIenTp06rppMdb9ChQoKNwROiAJMBY92oVfx+5imvqWy+n45Fks5427Qg+Xy0PjqmZ1acL9w7O7AXXHKUszC23vPcgLzN9jqQ1SHiCBgi0C1atXU3t/LL7+sLEC4b0G5YG9wGh+4QfA3JiaGunbtql7Y5C/BTvg4QIC15alg3+w8W8UtkMbBgWBZjnJHjhxRLygkHH5gfHzCSqVKlVJL6FdffVW1gPfPPvusuofr3ozLwVDuupw/f/4U5YjnHzlyZEroK/qEAsUhzIYNG5RljHHjNX78eOUeB9Hd5BxZ2e6Mw6dl2DQNmPCDpDrmx2AO30iy5P3jiiXDrIuWvyrWx6LDcvvXXx2OM+m2xTJkd6wlA7u2wL0Fr99jxL3FIWByQyHgqRuIWWFjBW7WoZl+XKZaAkPTLTqXSK/w8hWHHg+d2EaNd2t7JGHXr9tV/Mc4lA3LZDg15+JDjld4rw9JiMTqswuXXLRCwNFSL9hASsvJdLA9q6/HayoFOIXzdvTmZS+kCpOMfnNz253ntTqq1y+uZUr6ZqtvpCQ5+oVdW1pyvl0RQUAQEATcQcA0m2PYt3uT9+8g5bJmoHVNslDOg3u1Z+ANZ954uet5QEnfe5t20JGZ9/twOCLKz50plzKCgCCgIxBwBXg6zkK9tt2k6suvcUxvHNNeXaCFnKA8K7is+MhcyWuvEWXQhnqRl8av8pK39JJrtOe6RoCwmJUfiAxEBAFBQBDwBIGAa42J0TWIjmmkBNkz/kZrLy6kM/EfUMlzmYhpp4ng/2TlK/Y0E5YuYOJTCPJx/FA7syfPK2UFAUFAEEhBIOAWYETuAiqN5NiqUczld1QN7GYS+/1xmI6Sl5gGn/2PtrAzNGJ5ofxwwDGsQhRN4pA2EUFAEBAEvEUg4Bbg2xcW0dDmDdT4R+0/o/4Wy8yhTuyPpV5Msw/S0rZMdY+T4XtZWW5o5j7nn7fASD1BQBAIfQQCbgFaQ3w+gbn+WApFseL773+JPTppM2VTVPVQfpBx1Tyjug/9KZQnFAQEAW8RMI0CXH1hNyXcTuRlcFHKHM77fyyTwgpRIyZAiIm3UL1c4fRvy6x8SBJwo9VbrKWeICAImAwB02iTFRd2Kmha5q2q/k7nXLx92ScQ3C+IAZ7PJ8NIcC4iCAgCgoCvEDCNBbj03D/qmZrkqUQf7o9XSY6ysSvMyEpRtL9VNlF+vppxaUcQEARSEDCNBVggU06VHjOJailCA8gHlaPo+RKuOf9kPgUBQUAQ8AYB0yjAGbUGsOV3lp7eHE9RHNnxcZVoerZ4hDfPJHUEAUFAEHALAdMsgRMsGWjsocxqz2/wllnK8gsHi7CIICAICAJ+QsA0ChDszTjtjeJwuD6fvO6nx5VmBQFBQBC4g4ApFOC7e+PoowPxlCcxllYOeoDy5skucyQICAKCgN8RCLgC3MeEBkP2aJT3ff5ZRHX3M8tuMjW3359eOhAEBIF0jUDAD0Hm3dDyDID8pfsZzRWGajBBgoggECIIrFixQuXR1dNumuWxkKNYJ1Pt27cvJ/DT8o6YZXxGjCPgFuD16q3VczbNG0OVDvytPbMoQCPmXvpwggDYovU0jshzoQuSD+nX3Uk/iXpQgMjt4YkgWZOn/XjSPsr+9ttv1KxZM5W3wx3lZ51HWc8VbNun9bhtE6QDO+RUMZMEVgF2eIFzv5ZiPI7Qxosj6dr+XRo2ogDN9BlJN2NZuHAhwSqCIAE5J7RQr7/++ktd27VrF7377rt04cIFdf3XX39VSYg8kc3IleyGrFy5UvVx8+ZNh/1AsaZFkJoSKSrdFViLhw4dUuNq3bo19evX766qSCmqjxsYIfUnBAmU0M+JEyfc7cq4coHMWqInMPrt1CnLtVuxFkvWrBZLfU6CJCIIGIQA5/cFy4Z6NWrUyG6vL774orrOX2pVDnVYEah/45orQfIl1IF8+eWXdxWvz593vX/9r3UB2344M1xK+Q4dOrjq2uF96+dGv9ZiOx6MEaLjgH/r43LYgU15vRwnY3dWxfB7Ad8DrMD09531vYcpU4hq12b8RQQB/yOAJR3SYiIN5f79+6ldu3YqraNtjmA9+TlSOSIhOupAUM/T9I6wkrC0ZeVFc+fOpXXr1tl9UCwl7fWD8bGWUHXQDpaVffr0sduGs4tIy4l0oHghOTyWwcgpfPv27ZT2bet7kgQe40feZbNLYBVgYgK1zXCZMcqm4fTII2bHS8bnAQLHY8/Td8dXKJYfW8nAX96meSpT87xVbG+p95svH6AV53fSI4UaMgFuPrtlZp/eQNuvHE65h7YctWevASxHR4wYoRTADz/8oJa2w4YNSymK5S1bPfTxxx+ra1B4bMGp/Lvly5cntmZo3LhxVLNmTXvN270GJQMF9v7776ucurNmzUq1NIQygoJCOSQQf/zxxwl7bg8//DDlypVL1cNe2p9//qnG4o0CtDe4bt26qdy+ttnyihQpovrIkSOHvWqprm3btk1hg/zAZpfAKsBH8lEOnkBqMdTsOMn4vEDgx5OradDuGQ5rZs0YRdcemGn3frctn3LOl5NKeb5dzv4P47PbxzNP5LW76nuiALNly6YSdcNaqVWrVsr+HxqE8sM1KD0oSMiqVavo/vvvT1E4N27coDlz5nikAPWT4AIFCqj+XCmv6OhowmEL9tZgbcbHx9Pw4cPVNXcVkl2A7VyE8oPYKkC9aN68eVNqYf+QtwzstAIS95dUYvRgkMAqwGBASMboNQKPF26sFJg9CzCMwqhB7vIO255S8yVadn4H531p7LDM2Kp9aN/1Uyn3PVF+qFSvXj1l+WGp+cYbb6jlLywzSNeuXdXy8LvvvlPvYdHgYASWl76ZDwts6tSp6r67cvz4caVgcDBgu9TW24BihFtKpUqV1KVFixaljAOK8/vvv1fKD23o43O3/7SUK1euHPXv319ZoXrfsEbz5MnD3MVb1HWcKsMi1pUo/lq722zfvl3dM4vbTRh2HdMCSlrqYg8DJrwOVlrakrqCgDcI4DNobeV504aRdQYPHqwsQBHfICAWoG9wlFaCFIEA/v57hZgoP69gc1gpsH6AdQrQxEr7afPSH4n27HE4SLkhCAgCgoA/EAisAmxXkk5nuklH/vcqUcWKRImpTwv98dDSpiAgCAgCQCCwCrACZ39jabjnIufCZI904f+TT6UgIAgYiEBgFWDmCMp7NZ4KXWQKfPZxYs9JAx9duhIEBIH0jkBgFSCjX/R8rDYH7GYgIggIAoKAkQgEXAEWO8cKEOQHQoBg5LxLX4KAIMAIBFwB5rvCZKjNm8tkCAKCgCBgOAIBVYDR8UnUAAcgHOsoIggIAoKA0Qj4TAFakyUePHjQred48fF59HhSSaL69d0qL4UEAUEgdBD49NNPUxFBGP10PlOAX3/9tWLTQGxgmTJlCArRlXzEBT6U5a8rmEx3H6GLCCETCT4EMG9mCT0FoUPRokUV6cSrr75K8+bNo6tXrxoKqs8UYNasWRVbBQKiwRKxdOlSQx9EOhMEBIHgRADMO2PGjFGUXyB5eO6554yzDH1Fwcq8ailNPfroo5ZffvnFZdNgyuUpk5dgIJ8B+Qyk+gxUqVLF8uOPP7rUI2kp4DM2GNAIvf322+onCGY2mHNB6igiCAgCgoA9BBxto4BzEaw3jRs7pkKz154313zGBnPmzBnC4QcYb7EEFuXnzXRIHUEg/SLQuXNneu211wxRfDrKPrMAQZD41VdfqXbNssmafj9K8uSCgPkRAHlqRSZBac4HoXiB7NVo8ZkCNHrg0p8gIAgIAmlFwGenwGkdiNQXBAQBQcBoBEQBGo249CcICAKmQUAUoGmmQgYiCAgCRiMgCtBoxKU/QUAQMA0CogBNMxUyEEFAEDAaAZ/5AXo68JEjR6okz0hM3bt3b5WRXsQ8CHz22WcqrhuSKVMmGjhwYMrg4PKE/LDIW4v569ChA5UvX17lhNVz3SKPrp4E3DxPlb5GgjzHGzZsoIIFC6pE79OmTVOhqrogJzJyDCPxO0LR0qWkJYwkLXU56bSqzgmVLew4nZampK4fEHjnnXdSWmVldlcPkydPtnCkj7p26NAhFcKEvzKPfpgIL5tkYhI1L7q88sorlgULFqRqjUlMLLiXXiUgFiAiRvRfIvw6rVmzJl3++Jj5oa1ZOfLnz6+ifGApQI4dO6asPYjuvMpfIGrVqpVygmdlSPylEqs+gBOsR2TpQ0BY2alTpwIyori4OJo7dy7t2rVLfV6wOoiOjk41FlioiAaZPn06Xbt2jRo2bEj16tWjOXPm0L59+6h9+/Z3faamTJlCbdu2JY4Xplu3blGbNm3UZ/Tnn3+mkydP0hNPPJHymU3VWfKFgO8BAhyEzomYFwHMka78bEcZG6vldClVqpRSfnhB+bGFb1tU3gcQgUuXLlGhQoUCMoLx48erKLG33nqLmjRpQh9++KHdcYwaNYqKFy9ODz30kBorfmSh1PDZwjYLaLN27tyZUhefMyjIbt26KRqt6tWrExOxqHq4Dlo+KEJnEhAFiC8TJgSi/3U2SLlnPALZs2dP6RTWhLUU4xSmsAIhtveMH6n0aA8B0EpZr6z+/fdfe8UMubZ3716l/KKioqhy5crELFB2+71+/Tpt3LhRKb/u3burfeWqVatS7dq1lXLDSsRaASYlJdH27dspT5489Prrr6s2GzRooPae6yeTLB84cMBuX/rFgCyB0TlMYFgL2FD/7rvvnA5SbhqPAD6smB+IfkDVo0cPmjp1KrVr10790mLJi0MQ3selzZs30/z581V5mVPj58u2R3Bzjh49mvr27asUD36oYBmBhBRWFZaOkyZNUktTzOHMmTOpa9euts345D2WshgHlFqXLl2UUnMk5cqVS7mVN29epdx0gUVnvYzHM+IF0X+wCxcurN6DnxQSExOj/jqU9Lr5Kc8tCAgCxiHAisvy3nvvWdijwMJ7d3Y7Znbou67jUA2cobrYvrctz0rOggM6XWzf2+s0IEtgh9pYbggCgkBIIoDDzkGDBqm9wD59+pjmGUUBmmYqZCCCQGgigKX45cuX1cNhqwT5P8wi4bzPM9Qsg5FxCAKCQOghgMOLGTNm0JIlS6hGjRrKS8AeG3R4eLg6vdUF77H/jJNhCN7XrVtXJVLS31uXz5gxo9rn1F2z8P6+++6jfPnyOQRV+AAdQiM3BAFBINQRkCVwqM+wPJ8gIAg4REAUoENo5IYgIAiEOgKiAEN9huX5BAFBwCEC/wfONhHo1qveKQAAAABJRU5ErkJggg=="
}
},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"po_rilem = PullOutModel1D(n_e_x=300, w_max=0.12) # n_e_x - number of finite elements along the bond zone\n",
"po_rilem.n_e_x=400"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To configure the model such that it reflects the RILEM test we can either use the interactive editor above, or assign the \n",
"attributes directly. As apparent from the editor frame above, attributes `fixed_boundary` and `material model` are dropdown boxes offering several options. To assign these parameters we can use the following scheme\n",
" - assign one of the options available in the dropdown box to the attribute `attribute` as a string\n",
" - the option object is then available as an attribute with the name `attribute_` with the trailing underscore.\n",
" Thus, to define a trilinear bond-slip law we can proceed as follows"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"po_rilem.material_model = 'trilinear' # polymorphis attribute - there are several options to be chosen from\n",
"# set the parameters of the above defined tri-linear bond-slip law - add also the matrix and fiber stiffness \n",
"po_rilem.material_model_.E_m=28000 # [MPa]\n",
"po_rilem.material_model_.E_f=210000 # [MPa]\n",
"po_rilem.material_model_.tau_1=4\n",
"po_rilem.material_model_.s_1=1e-3\n",
"po_rilem.material_model_.tau_2=8\n",
"po_rilem.material_model_.s_2=0.12"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To set several parameters of the model component at once, the `trait_set` method can be used as an alternative to one-by-one assignement"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"d = 16.0 # [mm]\n",
"po_rilem.cross_section.trait_set(A_m=100*100, A_f=3.14*(d/2)**2, P_b=3.14*d)\n",
"po_rilem.geometry.L_x=5*d\n",
"po_rilem.fixed_boundary='loaded end (matrix)'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The configured model can be rendered anytime as a web-app to check the input parameters and to adjust them."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"po_rilem.interact()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Bond-slip law calibration/validation\n",
"\n",
"**Can we find just one material law that predicts all three tests?** \n",
" - The preconfigured bond-slip law with an ascending branch after reaching the strength of $\\tau_1 = 4$ MPa with the parameters $\\tau_1 = 4$ MPa, $\\tau_2 = 8$ MPa, $s_1 = 0.001$ mm, $s_1 = 0.12$ mm \n",
" can reproduce the test with $d = 16$ mm and $L_b = 5d = 80$ mm.\n",
" - To see the prediction for the test with $L_b = 10d = 160$ mm, modify the parameter `geometry.L_x = 160`. The result shows a good match with the experimentally observed response."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Can we compare the differences in one plot?**\n",
"\n",
" - The interactive user interface is illustrative and provides a quick orientation in the scope and functionality of the model. Once we have learned its structure, we can use the programming interface to run simulations in a loop and plot them in a single graph to see the similar picture as in the output of the RILEM test above.\n",
" \n",
" - Try to compare the third test with $d = 28$ mm and $L_b = 5d$ mm."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/step_by_step.png\" alt=\"Step by step\" width=\"40\" height=\"40\">\n",
" <b>Plot step by step</b> </div>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, (ax, ax_bond_slip) = plt.subplots(1,2, figsize=(8,3), tight_layout=True)\n",
"fig.canvas.header_visible = False\n",
"\n",
"print('calculate d=16 mm, L=5d')\n",
"d = 16.0 # [mm]\n",
"po_rilem.cross_section.trait_set(A_m=100*100, A_f=3.14*(d/2)**2, P_b=3.14*d)\n",
"po_rilem.w_max = 0.12\n",
"po_rilem.geometry.L_x=5*d\n",
"po_rilem.reset() # it is like pressing the reset button in the above window\n",
"po_rilem.run() # like pressing the run button\n",
"po_rilem.history.plot_Pw(ax, color='blue')\n",
"\n",
"print('calculate d=16 mm, L=10d')\n",
"d = 16.0 # [mm]\n",
"po_rilem.cross_section.trait_set(A_m=100*100, A_f=3.14*(d/2)**2, P_b=3.14*d)\n",
"po_rilem.w_max = 0.12\n",
"po_rilem.geometry.L_x=10*d\n",
"po_rilem.reset()\n",
"po_rilem.run()\n",
"po_rilem.hist.plot_Pw(ax, color='red')\n",
"\n",
"print('calculate d=28 mm, L=3d')\n",
"d = 28.0 # [mm]\n",
"po_rilem.cross_section.trait_set(A_m=100*100, A_f=3.14*(d/2)**2, P_b=3.14*d)\n",
"po_rilem.geometry.L_x=3*d\n",
"po_rilem.w_max = 0.05\n",
"po_rilem.reset()\n",
"po_rilem.run()\n",
"po_rilem.hist.plot_Pw(ax, color='green')\n",
"po_rilem.material_model_.plot(ax_bond_slip)\n",
"\n",
"# The code sequence can be certainly shortened by using the loop. \n",
"# It is deliberately omitted here as the focus is not on programming."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Comments** on the study\n",
" - Note that the bond-slip law that can fit all three pull-out tests exhibits hardening. \n",
" - The maximum control displacement `w_max` is set equal to the one applied in the test as no information beyond this value is provided by the tests.\n",
" - The trilinear bond-slip law does not give us the flexibility to reproduce the pull-out failure\n",
" as it ends with a plateu.\n",
" \n",
"## **Need for a more flexible bond-slip law**\n",
" - A more flexibility is provided by a `multilinear` material model for which a list of `s_data` and `tau_data` \n",
" can be specified.\n",
" - The `multilinear` material model is used in the following code to show how to achieve a pull-out failure by introducing a descending branch in the bond-slip law.\n",
" - Note that for bond-slip laws with descending branch, convergence problems can occur when approaching the pullout failure. The convergence behavior can be improved by refining the spatial discretization given by the number of finite elements along the bond zone `n_e_x` and by the size of the time step\n",
" `time_line.step`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, (ax, ax_bond_slip) = plt.subplots(1,2, figsize=(8,3), tight_layout=True)\n",
"fig.canvas.header_visible = False\n",
"d = 32.0 # [mm]\n",
"po_rilem.w_max = 0.12\n",
"po_rilem.time_line.step = 0.05\n",
"po_rilem.material_model='multilinear'\n",
"po_rilem.material_model_.trait_set(E_m=28000, E_f=210000, tau_data='0, 4, 6, 0, 0', s_data='0, 1e-3, 0.08, 0.12, 0.2')\n",
"po_rilem.geometry.L_x=5*d\n",
"po_rilem.reset()\n",
"po_rilem.run()\n",
"po_rilem.hist.plot_Pw(ax, color='magenta')\n",
"po_rilem.material_model_.plot(ax_bond_slip)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Questions:** Effect of bond length on the pullout response - **bond hardening**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" - The iterative trial and error fitting is tedious. **How to design a test from which we can directly obtain the bond-slip law?**\n",
" Comparing the test with $L_b = 5d$ and $L_b = 10d$, we recognize that the shorter bond length resembles more the shape of the bond-slip law. To verify this, set the bond length in the above example to $L_\\mathrm{b} = 1d$.\n",
" - On the other hand, if we increase the length, the maximum pull-out will increase. **How can we determine the bond length at which the steel bar will yield?**. A simple and quick answer to this question can be provided by reusing the analytical pull-out model with a constant bond-slip law as a first approximation. The maximum achievable pull-out force of a test with an embedded length $L_\\mathrm{b}$ is given as\n",
"\\begin{align}\n",
"\\label{EQ:MaxEmbeddedLength}\n",
"P_{L} = \\bar{\\tau} p_\\mathrm{b} L_\\mathrm{b}\n",
"\\end{align}\n",
"where $p_\\mathrm{b}$ denotes the perimeter, equal in all experiments. The force at which the reinforcement attains the strength $\\sigma_{\\mathrm{f},\\mathrm{mu}}$ and breaks is\n",
"\\begin{align}\n",
"P_{\\mathrm{f},\\mathrm{mu}} = \\sigma_{\\mathrm{f},\\mathrm{mu}} A_\\mathrm{f}\n",
"\\end{align}\n",
"so that the bond length at which the reinforcement will fail is obtained by requiring $P_L = P_{\\mathrm{f},\\mathrm{mu}}$ which renders \n",
"\\begin{align}\n",
"\\label{EQ:ConstantBondAnchorageLength}\n",
"L_{\\mathrm{b}} = \\frac{\\sigma_{\\mathrm{f},\\mathrm{mu}} A_\\mathrm{f} }\n",
"{\\bar{\\tau} p}.\n",
"\\end{align}\n",
"For a generally nonlinear bond-slip law, we need to evaluate the maximum load numerically. Two examples quantifying the effect of the bond-length for bond-hardening and bond-softening systematically are provided in the notebook [3.2 Anchorage length](3_2_anchorage_length.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"cfrp_sheet_test\"></a>\n",
"# **Studies 2: Softening bond-slip law**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[](https://moodle.rwth-aachen.de/mod/page/view.php?id=551816) part 3"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The presence of the descending branch in a constitutive law is the key for understanding the propagating debonding. Let us use the established framework to study the different phenomenology that occurs for constitutive laws exhibiting softening. \n",
"Consider an interface between a fiber reinforced polymer (FRP) sheet used for retrofitting of RC structure. The study is based on a paper by [Dai et al. (2005)](../papers/dai_frp_pullout_2005.pdf). The goal of the paper is to derive constitutive laws capturing the bond-slip behavior of the adhesive between the FRP sheet and concrete surface. We will use selected experimental pullout curves from the paper to reproduce them using the numerical pullout model introduced above by verifying the bond-slip law derived in the paper."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Test setup"
]
},
{
"attachments": {
"974c60ea-69f6-4175-ab89-cea30a6bf1d6.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAigAAAEBCAYAAABSRl7mAACzG0lEQVR4nO29B7h1VXnvO5OTnmNDsYHYDViwAPYuYo1ib0eNMWpi7FjjTTR6jDEarIkFNTbs5lpAoyKIShVRLCAoqAiIiiUmnsSckstv3vvb9/+9zrX22vvb3/72t/f7f571rLVmGXPMMccc73+8bfzaf16ModFoNBqNzYNf2dkVaGw/fm1nV6DRaDQajcb/i5NOOulmF+OknV2PjYAmKI1Go9FobBA885nP/Jt3vvOdD91jjz3O39l12dlogtJoNBqNxgbA+eefv8fnPve5W7/vfe97wFOe8pRX7Oz67Gw0QWk0Go1GYwPgAx/4wP3+z//5P7/6/ve///5NUJqgNBqNRqOxIYDmhO8TTjjhFmhTtrqZpwlKo9FoNBo7GRCS448//pb8Vovy5Cc/+ZU7u147E01QGo1Go9HYydC843+0KU1QGo1Go9Fo7FSgMcn/beZpgtJoNBqNxk4FROS44467VW5rM08TlEaj0Wg0diqqeUdsdTNPE5RGo9FoNHYiqnlHbHUzTxOURqPRaDR2Ei644IIrV/OO2OpmniYojUaj0WjsJEBApsw7YiubeZqgNBqNRqOxkzDLvCO2spmnCUpjl8d//ud/Dr/yK9Orq7MPzNq/2uuttkzrOq/Oa4EdXX6j0dh+zDPviK1s5mmC0tglgMDl86u/+qtLBCH3KfRTMPvt8bkvzxH1eH9zzTzn4gFj+J//838u/U4iUOs2tb1e5zd+4zeWrlHvKX9nfeu+RC2/3mfdl9+NRmP9sJx5R2xVM08TlMYuAQV0EgIJCfiP//iPpW2/+MUvhv/9v//3+P9//a//Nfzrv/7reB77OO6f//mfx/8SjZ/97Gfj8fzn+0c/+tHw85//fOmaVYhT/g9/+MOlc9j+X/7Lf1m6Jtu4Lt+//uu//ksakyRTkJNLXOISw2//9m8vXd/7AOz/3d/93fEYz/+t3/qtYbfddhtJzX/9r/91PJfjOZffbAO/+Zu/OX447td+7dfGD2XwP++r0WjsHCxn3hFb1czTBKWxS0Di8eMf/3j4t3/7t5EA8BuCgWD+6U9/OvyP//E/RiEP4eA3AthzJCQQlH/5l39ZEuiSDP5Tpt8AQc4HIc82juW/ZVUtDL8hAfz/93//9/E/BKVqQDg3AQkR7IPsWBf3sS01RGxnG2REcsQH8vI7v/M743Hsg9xQJ35Dcvh/qUtdajzmcpe73HDZy152vD/KaDQa64fvfe97V1rOvCO2qpmnCUpjQwEBrYaCD+QCjcfFL/Pwk5/8ZPwPyUAYo+XgW1Kh1kJziWRCc4zbJCBso6w0r0g8ENgSCupDGZ4jIclrSUAoz3O9ttfNa3gMkPywjeO8vyyP79S8UCe2ox3yPiUxamL4DfmwbEgNZEXNCkSFz9WudrXhRje60XCNa1xjm3o1Go0dhxNPPPHmN77xjb9Yt188ufqdiyc4v7Xbbrv9OLefeeaZv7d+tdsYaILS2FCAgHzgAx8YvvzlL49COU00CFqFuVoIvxGsSRjUXHC8BAXhnOcmkeBbrYUCX6LCdn1f0p8l/WKAdbMctTSSDsqiXhIGzTnWheMkNIJj2KbmhGO8V0mMGhPvG+IGJDqWax3QLrENUxbHQ/7Yvueee45lNRqNHY/73Oc+/zefuv2d73znQ4888sh7HH744Q/bGfXaSGiC0thQwHxz4YUXLplrEPYKZjUkkgK1BNXsImGAkACEswRDjUlqQup3+rukOUbtRB5Xr5nnqdGQiLBPgqR2xXPdJxkC6b/ivfhbnxvbTP8STEtAsqb/ifdEnfIjabN+jUajsVHQBKWx4YBg1tETQSzBQBDzHyGcfhcgtR4IXYU8Zg3NI/qEqDFRAwHSvyQFtlqYFPAek1oWkFE+fLIebkuzjnWw/vznXtnHuZZbnVr5r4aI8zXbSE5yvyREgpNEyughysBkVKOgGo1GY2eiCUpjQ0HhqllGk4bOqsD/aWZRuGu2UXtgZItle1xqRqa0JHm8JMD9EAi1Ix7nf0mO29Pp1W3pNAusL8fi5OpxOtx6L57DdgiFv9O8lWVKTqYijdhOO0BSaFe+k7A1Go3GzkYTlMaGAuREAgLSjKLvBpAoZF4UzRaSAoW3ZUhY0nE0/URSw5Fmmqo5sdzMLZLkR6iBSbKUWpV0evWe3D8V7WMZeQ3bw7pLdiw/nX3VOEm2jBBiG5FP+s40SWk0GhsBTVAaGwoITRw1+U7/jUzSlhqK1FoomFNoa9LxvCQ/EgM1FW7j2pIfnWcV9rX8jJxJMqKwF6kxsQ5p3kkH3SRJEqPUFKnp8Hh9WdyffiW2lcdbd4mavjCYwZqcNBqNjYQmKI0NhyQFCl6Fbs2wqvCGiCisq5NpEoKMdqnEAuiYm2G/qV1Jh9waSZTanqkkb5IPzTdqNLxGHgc0HWlScr9t4j14bHWETa2K9y6RS9+c1No0SWk0GhsFTVAaGwoKT51MdQBVGOs/IqlI3w8FP9AMkz4hEh+QUS7+ThLi8anBSK1EajkkGekkq4lpKhzZ89Ro5LkgQ4pB5iahHYxm0r+EbZbpsbShPjmWmU60aY7iPBLdEdp9pStdabjmNa+5VGaj0WjsLDRBaWwoIFivfOUrD1e4whWWQo0V7modFMJqAMwvooZAPxaFsPk/cEDlN+VyrPlDzEZLllVT3OuQqzklw5JBRutkKK/ngAwZNlur9ZdMqOVJ4uRxaeJJx1yuJUkBEjW1R6ml4Z4ldd/+9reH73//+0t1TmJ37LHHkn9h+NM//dPh6le/+ro970aj0ZiFJiiNDQUE+W1uc5tRSJK07aKLLhrOO++8McQYR06zuiJkSeAmgeC8jGzRl0RTiEJerUU6x6ptqHlVFN4K/fRlSZ8XNSTpUJtkiW+1QJqa1Gak6SY1NiDDgCUckheIR/rK6LdjKDVki+2XvOQlx99EMh144IEsOjZ88YtfXNKepLPvLW5xi+FhD3vYEjnLfC+NRqOx3miC0thQQBgiTK997WsvOXBCTiAf5kFBA8J/hDwaD7YjVMmM6jo7rtfD8Ryb3+kXApLEcO0kNpkHxay0aarJbK2SIrPFWkZG7/DNNsN6PU9NigTDDLGA63J/u++++7iN35AO1tKRBEFEJBZ8cxxlSGS8V8w3r3zlK4fjjz9+G4dj8s7w+9RTTx322WefMQW+mpiqOWo0Go31QBOUxoZCDZdF2CJkU0hOCcwM17Wc/EBmIC2s7/Od73znl3xCJBQIc4Q131yX8jmPMiBDkByFOmToW9/61vCDH/xgiXDc4AY3GK54xSv+Uk6STBwHmdBMkynxPQ7CwX4W9/Ne1PSw79KXvvQ2i/tVx9Zqjsrjbn7zm49r77zkJS8ZjjzyyJFg7bfffsNTn/rUkdSceOKJw4c+9KHRzHa9611vuNa1rjXej7lkGo1GY73QBKWxoZCkIVEdSOu2NLdkSLCCWm0EglYyUJO1SQLQTkgSqllHnxUWMDzrrLNGbY7OvJyDML/85S8/lilpsX5qTiA+dVG+GmJctRcZJpzRQdkOtb2mHG+pJ2vuPPOZzxzrg2PsM57xjNG8w/UgKxdccMFwyimnsMT78LnPfW4kNBCvq171qsNuu+22TT3zWvPq02g0GitFE5TGhsUswTtvW91f/2dkj/4e/s6IGlC1EEbC4Gz69a9/fTQpoV2RDOlj4rHpp5JCXafWeo1KSlIrlM6vixKAee1CtM4hhxwyOs1e//rX3ybHCwSG/Xe6053GdZHQOGES+sQnPjFqViAxe+2116hp0oelEqkmKY1GY3vRBKWxpaAWwVT6EhOQafUVtBIYTCGs+ouDKRoGjtPck064Gfqcmo4atjulKUlnW5A5VWaRptWCa0BCIBxTZII6YWKChGDmucMd7jD85Cc/GTUrONpSD4gK+9Cq4LOiGajJSaPRWAs0QWlsKaQJyJDdqWRnmoAw0eC38o1vfGM499xzx0giE58ZnWPI85TGBeQ6Pqk9qSnvM2eL52aq+mraWes2SVQzGvW47GUvOxx00EGjOYjIKggbZi40SbQHkVcQFjQwtkuj0WisFk1QGlsKU2aTXCRPh1UEMuacs88+exTCEBPMOfqlZIhy5mbJMGavkeHNbkuNiWTIXCqZxC3rBdZK6M8jO8ttx0mXz9577z0SM5K8ffe73x3b6m1ve9uoebnJTW4yXPe61x21K7n+0FreQ6PR2NxogtLYUsika5mwDEEL2YAUMPvnP06imDQ040BYDDvG6RYTj0QlE7eZdC01NUlikhzUNPRAMpJJ6naU9mR7wP1g1uGDc/CNb3zjUZtCm5122mnDySefPDrY8sHBFg1Mmro22v00Go2NhSYojS0DSYDmmapNSR8UyAcmDLQDqSkhakchy39/49NicrQaEg3hMfNrmnNyLaBKmkD+to4bFfr2kAH4Hve4x9hOhF9jGvvKV74yfOYznxn9VNC63PCGNxw1MO1M22g05qEJSmOXx3KOozWcN/0q0k8kU9VLLNSqAMkNYcIZolwX2ssIHTUnmTFW4lHDc9XAuL2GT9dcLzsbNYQ52xnnWj5oTjCNYQLCwRiictJJJw3Xuc51xmR8e+yxx0jssv1nXWcR4CcE+TGHzCLn1jat/WUWZh13/vnnj9/c26J1mKrTFIGrfWJWfQB9iTw99GMcoiHJ3/zmN8eEf4bCNxobGU1QGrs8FPp8o8kgBX4Vmv7HTMO3xEMSYTl5rPsx90hOdHhNh1YEgEIDIcDHtPSel2HMCY5FgOcqyTrv6pdiOZhSNuIifvMEMHWHgPze7/3e+EGzQtjyV7/61eFjH/vYUjQRmpVrXOMaI6lZraaIdnv+858/POABDxjucpe7zK3XLAIw61iwyLE8pze+8Y2jqetVr3rV4pWfc93EvCR8WUdNkS972ctGokRIOdpA2ude97rX8PCHP3y76tZorAeaoDQ2BRiYyez66U9/epyha35JwY+Av8pVrjKmcjc77ZQjqqYWyYahwBIFE7NBXCQvSUBSA2LdgGW66CFkirqSLA2TEtshUOxzRWeJEjPeW9/61qOQ3xXhc8B3B+dZNCgITMjK1772teGoo44aiR4kBbLCczLl/0pACDhrOC0CMgNDJDA9kd13ihjxLCiPYy9zmcuMmpnMDCx4rlyb+yMcWy3KasF10QbRZjx7SF5tC/oKZjT6EVoR7kHYB3Hupk4uG0GCQdeBajQ2OpqgNHZ5MBAzM3/ve987vOMd7xgHZYQ9Ak8hr6PrTW9601E4ugifJCK1I+nA6kfi4Xo8+pQkcRF5TtXO+JvjEWKsIIyQdqFDyZSZab0GghuhTRhv3nct2+0bybejJm/TX4W1hPjsu+++IwFAIKNZec973jMSSNYNgszg14KQnWcGShg1NetYNFZHHHHEGHFEojoIyhOe8IQxhDqXVYBAveENbxg++tGPjudAAh772McOd7vb3UYCCTiW54i25LOf/exIYgjBXg2R9LoQnVe84hVjeWwjbPtv//Zvx+dvW55zzjmjdgRnZLbRp5/2tKeNSfey31ZNohq6RmNXQBOUxi4PTTtkPUXQmVhNTQVQy5FhvUbg+DvTwasBUdgBhZKrKauBMWrH/ZpnvGYuJJgaGzQ+zGi9B0iKvwHncS2ISq62LOkC89T9WdbOxqw8K4B24YPvCOv/YKLDuRZ/iQ984APjMWhV9t9//zGx3HLZdKeWA0iTDiQI4X6jG91oNHV84QtfGF760peORIBIJOv3pS99afjgBz84HHzwwWMkEkQFInKrW91qjEiiPJ4LaxodffTRw1Oe8pRRo8ExEs6Vgn7LPUOg/vIv/3Jsl8MPP3yMKKN+AA0IxJZlCP7kT/5kJG+sn/SmN71peMELXjBqeTKPTiWyG9nZutFINEFp7PJgAMZ34d73vvcovIkaIbkaJh20KAp1hAxCydWK0/wjichcJAgZNSRqSdJ5NUmMviE5Y60mIwkLYD8zd5KbQawQOq6UzDGuBYTAYlbPDJlvBFfNNFsJCeeS+RVhvitBwke7QEZY/4e2OfPMM0cnW0jAPe95z5EczIJmtHkOpGhqaO/HPOYxY74WFlDEeReHUv7bppAltBKYbE4//fTxPJY5SCKJ5g6Cc7Ob3Wx44AMfOJJOlgXgua0UJvzjfiFK97nPfcZttIPrNwG0OeScgQxBVOgzaHG4d8gdph41euzTDKlWrzUojV0FTVAamwIIc8wBmEAQGgzi6SsgiWGwRoUu1LBYhnlJAIJOsqBfiCnuNQfpJ5Fmnan1fBSQlEk5/Edlz6zbtPsgBUlqATRX4VhKqnkEUvWz0RkXwYYZYldEthf3TBQQ6/7Qbjy7RVZVnjJjpAbFCC36A0ADQbvxHPL6n/rUp4a//uu/HomeUS9qy7J86oVpR+dryl3UD2aqjjxH6mQ/4je+Mpi6MhydcO1HPvKRY90xa1JHtFAgTZhpymw0diU0QWns8siwYQQYs80p9bpOg5p+MqS3kgLKohwJCL81CUlkNC15DMQl853UPCYZImp98cFwXyZmq4sLup8IFQTR3//9349+CNbfdYCI2OAY84xMtUE1f2wUzFvJWjPQcuD+0CJAUm03nl36r9A2EFhMJGzHlMPxkIwsBzLINfE7wf8E0w3aufQ3omycrvEXQcsCceQYzDH2g0XbmmvSl3iGH/nIR4bjjjturCu+MvSVP//zP1/q30Q+cR3IEL//8R//cTQXHnjggWNZqUGxDTdiqHqjMQ9NUBqbDssJhJxhqy0xJb3+JwoWVfUSB2ejalFM465DK/s5J0OKNe1MOS6mL0mmy7dO3o/CjmgOTFkQm9e97nXDqaeeupSqH8GFeh9fCYgYpgFm3ZoGFmmbXR34IL3mNa8Z/Tg0l/3xH//xcL/73W/cT9vilEsyuUMPPXR47WtfO5ITQm9Z/DBx29vedjj22GOHv/iLv1jSnFVtBASGsojEQpvBfxxvcWpeDTj//ve//2jmod72sZe//OVLxJvvBz/4wcMZZ5wxPOc5zxnPwyzGb0mc/Yh+iQYmSfciWqhGYyOgCUpjyyBNPnwzUOv7kYJHkwlEQ/8SzT36N2jbl1To+1D9QlKb4jFJROpxGREkyVFzAxBWkBTyfOCXwqwa/wnq+Gd/9mejoMVXgnTzn/jEJ0aBhCmAWb4mAITYco6muyqIdsH/yHbk/nGwFdwzPiw4kz70oQ8dyQTtQvvQhmnigXDgy4OminPQVOCngjZF0I6ce9hhh41kkbWH9AOq0UuLgPKIACKXCteFcEF20O5k3XimRK1Rf7RBJrzLSCnagPukz9AOmLWISoLMNDYubnSjG33pEpe4xL/s7HpsBDRBaWwppOYktSdp/+djOLGQIJi/JGeoOWtNHwFJgFqZjBzKuqQWRfKTPikeoz+M+3GwfdaznjWaEyBL+J6gWUHgoj3BD4IQZj6YM9AUIFw5HnKDdqXmGkkNTtZtVwB1xeF1ihTkf4kfbcSn7vc3z41Q59SGsOZQHuPzguwS3SNWktytXlctCcRn1n7AMfjozCqL+ltfoR9LY+Piute97ul8dnY9NgKaoDS2FJJEINTT90MnU31AzOKaydfchubFSB81IqmdUQuTmg9geYYiZzQRSD+V1KRAgswkm4KKvBeQFOrOLN/741hm1cz6MV0wE7/ooovGKBQSoxE+C1k54IADxtwwhKbWPCOr0QDsbCzq8zHrmCmiMq+8RcpZFPNI1WqxI8psNNYLTVAaWwrVrJK5RQwn1pRjtE2ewzb9TnSKNX2+At79NRJHcgMy70pqTdJxF3A8PgQ6emY0iqQIs0LeXxVC1Bn1PscR5XSnO91pDFH9+te/PvoxsOowzpZEFaEtYJbNsZCczpnRaDR2FpqgNLYcjOCRRBgBk1qN1Gwo8F0oUE0Ktn+QQjzT2afpCMxyjk2TikRFx1vIiUQJTJlg5plkat4Ly0b1DxG55S1vOZqCWLlZ3xVMQaadx8zAsZCVJEdT12o0Go21RBOUxpZCajjSMVXBq4Yj/UY8j/+ulaO2Q1TNjKG//td3RM1JDT9O8mK0BSRhanHAlartZ5kt+LjSLWQFfwxIFzk3iCJBs0JEEAnu8K/A34EoIfPBVO1KE5ZGo7GWaILS2FIwp4bhwCBT06ffhQ6tfmd0j0RDIqM5JI+rockSGqNokuAI9hGNsZqF8ra3XbgXTD18ICN3vvOdxyyqpJwnVwi5PiBOJC6D0OBsi9/LRl1ludFo7NpogtLYUnBV12rK0e8knWg1/5gADtOHZheSgQGJhloPfViAqeslG2xP00/6t6SvSU2bvzOgKQgCgj8KqddxtCURGYTlxBNPHE1DEBVCXnHWJYR50QX9Go1GYzk0QWlsOWiikYCkhiRzj5gkK809hhhLRNIZ1vVzANvMPqsJyTwpufaPeVUgQJSB4y0amgxXnhL4nK/D7lpgll9JmoL4kI+DvCKYgvBbIVfHF7/4xTEtPL4q1772tcc8HuTa4P7VFs27ZqPRaEyhCUpjy6E6jaapJZ1XJSmQBx1fzZECELxoPUzwZaZRtS4ZomyZmRSO4wn7Pe+888Y6oKHwOM1OZqzNNX4oj1wnhA/jyLrepiDulw+mIAgJSePQpkBW8F057bTTxntE8wJZIecKmhgXbhS7Wghzo7EjcPH7cstTTjnl/vOOudzlLnfRbW972/dcPEE4e73qtRHQBKWxpWBosRqKNOvwW/KBFgOTDqYcs5LqvyJxQEiTP8TVYtEqGHrMx4ifXGCOY/lwLOnRyUlCyC/XMHOtqLlV1JZAmCAzJBFbbyFfr+dvyAgfVotmTRiIF1lXMQWddNJJI0FhdWAcbvndPiuNxv+LI4444v+6+L2/G2PBLOyzzz7/8+Ix42YPfvCD772OVdvpaILS2NSoC6ORBp1wWkmJZAXioXkF4UkKcY4DhiETwcM3mgCOp+x/+Zd/2SYyCE2CeVHSP8W6uB2tCQIcqGlBIwHx0NTEdTjeOvFfYsR3ZrpdLyQ5SdON22kXEsCR0fYmN7nJSMRIEMfge8IJJ4wL8LEfckUmXHxYIHlqodJJeTUZbectkDjr+Br23VqdxjrjV8n0fNRRR8084HGPe9znb3jDG/7rOtZpQ6AJSmPTI4UdBOL4448fBac+HpALNSOSEIS/WpAMNU4TjyYgiIVOt1/96ldH8gA8D+GbafU1+1AH/UggIYYw47+hiUmkySmjjjYq9NOhbTCD7bXXXsNBBx00RgWhOaKdWLsGx1oy3hIZRKI4/kPEVpsgLlcQTrJRiUc1NeXSBI1GY2OgCUpj0yOFEeSBGb2mHQmKJCNXrNVfBHAMghOzD2RCfxCjfziW32hUXKMHsE/fEsvILLFcL4kPH7ZJPjTrsD/T6uuwuysgM+miPWEBvlvc4hajKejCCy8cNVXkXGEGiRMu2hWigvRbWRS060c+8pHRLwZHXkkK5iZCpH//939/LD/xjW98YzjuuOOGgw8+eCRHWd9Go7Fz0QSlsWmBcMKHBOdNTDYI/7POOmskEQh7tRdoLly1GALCh4RkkIEMSVbTkk6yajXYxrU4N51ac90ezUQpACmfT4YWcwzfaB3w2dC8g0kIgZ75VnYFVHONzsV8iPzZd999x/ZBu3X22WePPiuf/OQnRzLDPhyB8W9Bs7RcfpjXvva1wz3ucY8xpb9mOMxLf//3fz86FSdBoZyf/vSnw+mnnz6uAi2mzEQeX5GLAs5aIDCT+M16ZnVV63SIbjS2KpqgNDYddIQlZwe2XUwJZEeFCKD9UEORocMSFskERMO8JpbJcbk+j6YWhBznYbJJh1v9TxQybksThBqa3Ea5JGsjwyvaANfhMSU9+9YqvHhHYZaQr/szZJvIJIgI6fVZgRkz0DHHHDO89a1vXYpaImJo3oq86eic/iW5cKPXBZiWDjzwwJEssQ0fpc9//vNjfSBLmJ/Q9kCWsu70ha985Stj/4LMou0xYinBdVnv6DOf+cxIjHEUJisv5+Q90HeOPfbYMWSbunDN/ffff4msNFFpbEVs7FGu0VglMOMcccQRo3BIEqCTa/ocIBDYpskkyQffOqUitMyZopDSLGQ5/NeMw361LpIio3H4mFOFbUTmcAznIbyY6aNd4FvzD9/py1LX8dmoSE2AvjNGSUHuiGKCGKDl4r9J8Gg3zC58MMHRFstF/9CGEAfyspgoD+dc6wFS20FI9Ktf/eoxzT/PAG3Kn/7pn47aK/5DlA455JDhEY94xJL2hmdw9NFHDy960YuW/kOGn/KUp4yEMq9xwQUXDH/2Z382EljI14c+9KHR1PSkJz1pKfcN50NOnv/854/mLfru+973vrH/ojVqNLYqmqA0Nh0Y9PH7IFIGIZirFOv3kap0haZ5Tswia7I1w4glH/qdMOvVHwUgUDPPideTSNT1ery+51kHFxykHLYj3BCOanO4JvXaKCYe70siRbvwod4/+9nPxt/4mxi2zTa0CeznWSCoIWVoKXCURUMCOSO6x8y680woCdoGPxQcoT2O66LhSKdjQR3QrpkwzxDwxzzmMcO9733v4elPf/qo/bj//e+/5KPCOVyDur3zne8cz3/sYx+75Byd4Dj8XCA5aGM+/OEPD+9973uHBz3oQeNyAoDnzTHU8773ve/YHmhvcpHIRmMroglKY1PCgT19NYzOAQi9XCxQQuBx/E9NiGVyjKTHCB+zxZrELP0N1LpIcMw2yzEIIKAfTO7T8VZnXo5FQ6MfC0JsUUytppzbp47PzLISEOqiAFf7gdmJb0O0JR3ch21C3c0Zw/o9aAX4jVaE++C+8vjlnuk88Mwe8IAHDA972MOWBDxk5S1vecvMe66aFX1fqBukAq1KnsfzpA2ue93rjsSKa2LeyZw6Ag0N5Oz973//ko8Tprtc94n7Zt0jTFovfOELx3qbT4a2aTS2KpqgNDYlJA4IAIQJvzXBTJlH9ElBOGhukZAA15hJp1mJj9oNNSCmrNdPRA2AGpgs03wmLmCYhEBnW8mQ5UliFnGinMolkoTFbwlUahHQQiFQjbZBU6AJJokThAMfEQQvxANTDH4yprqXeGlSyxDgtdYQcB3yq+C/YR4ZSFS2wRRBy+2Zg6b2E+vNdWgbNVyET6P9qcehucGn5nnPe96ogcGcRduiIaqOw4985COHhzzkIcPHP/7x4R3veMdwy1vecty2UTRljcZ6owlKY9MhHSM1z/BfB9jUlGSSNoSrQhro8yGxyOgchAyQlIDUtnAe11NA6zCrYAfUjW0cY8SQZEQNiYLOyJ7VQNOLxIOyIB2YWQybxuzCbzVEOvzSJhA7NAX4RyBw2QYB4WMkVHVArXWtpGBHCd2aH4brmVdFYpr1mcJUptz8zbMhCR0RQ694xStGwoafC068XtNjMRMdeeSRw2GHHTaGThOdBJG7+c1vvo0v0yc+8YmRlNzvfvdbCnvHZ6WW12hsJTRBaWw6pA9Jmln0k0Agu4idwtRU9Wxjv1oKzTYepzag5kzhPLUugP36iXic9dF0JFnRjwVNROYMsd461KLRcCFBHSy9X0B5mljQdPBhZk/kD1oEBKnEgzpQBmQDnw+EIY6h1AFCoumF47jneQv+TQnQWQJ1RwtatCeQqDRRIezZrkktyRP3yz5JJu1BaLfHQiZo09Ra8Zu8KTyTd73rXWP5aJCSiHptVnp+2tOeNhx++OGjuYdVoR/96EeP5M5jOI8wZxxq8VmhDjjqEl3UxKSxldEEpbEpoWbEiB3DTxH4zqgz2Vn6ihgmrD+Jx/LNNoiCs3RNIpp2zI2SvheahZKk6FCZM3rIA8dCbNBieIxOvUb56HxKhBIEBG0IdeK3JItrIzgRdmg/ELSYGDS9QED4WEf9P1YjEDeKEKUe+HBwj0kqMbG87GUvG80qta5oMoi8ITU/bYzvx6GHHjqGH9OOOK3SF9Lnh2dE4jcifB7/+MePz+PNb37z6F+TxAjQ13CIhWzwTLlORubY5jjMPve5zx2fIXXP9Yo2Svs2GuuNJiiNTYmcJbuWjinn1aTkt8QiQ0mzLNPgm9Qt/U0A29FYQAjUbiCQclbt7FuNitcx1b2+HWguNL2QWM7rkhFVAWZqfv0cEHAIP0gJAlrNR9YRpPllSvOxq5sTIAkVPA8jZipoLz4C8oYGRWhmSdCmXIdoHDQe9B00Jbe73e1+6ViJKgSxOh/Pq8sszVSjsZXQBKWxKZEhxP72fzo6mrwN6BNgtljJg+fqz6KmRVKD+YSQZrQaZDA1usfVifmfzqFsx//DMGXNPRnuDMGAsOB4iYAlsoTrkS+E35AYZuW3uc1tlkhVCrMq3KYic6YcRjeDQJzyd1nUf2fq/qtTMccccMABw0tf+tJxXSH6CxE9aGjmlbmc38ssv51GY6uiCUpj08GBXbNOJmBLbYkZR81XorZDHxGdZPmQRIwoFjQk+BtwHKQEwoCJRTMOx1mOae0186itAWp0JEpoQdB8MGPXhwGhxwcwsyZlO34MrlFDXaqDam2D1f7fVbGcg+v2liloc3xX+Kzm/O05rtHYKmiC0tiUqGvVqJ2AlKS/hRoVNBJsN8cHZAFTDGGh3/3ud0eygbYDMoIzo4sAZlQO10OLAknRxMLsOs0+mpFcvyc1K6r3OZZj+O96MkZ7SHDMkdJoNBqbFU1QGpsOmi9MzIYg1xfDxFgQCAmCZh41KZAIiAkftCb8hzRonjHs1+yjNbcHUTE6Qlom53Ou+TXMe5Kh0JQJqCvnW8fU6HCea/G4fkyj0WhsRjRBaWwqZA4To2AkK0kizGOSYcOGEQN8C3Rk1YkVokB0B9EwamPQophXhOu5DVONRER/FslKTV+vSQdfFciHmhNJlflTdNbltwRnV1iLp9FoNFaDJiiNTYUkIaaH1wnWMF9NO/qHqMHIlYtd2djIG4gDTpCmwZdAQFpMqc75OL+aZyRT6VtmDWfmf5InysY5Vs1KptDnXqwPvilEprQGpdFobFY0QWlsShi5oTOsSdNMiiYh0bfEhQJ1XmVtFUJ62aZGw+gcs79qIsqEcK64axp0j0+nXMmK66yY90Rzkw61Eh2ThJHJFfMRYbCQE85rNBqNzYomKI1NC51LEfJqQzSRpGOrJh7DjiEPmHGIllHTkeWlyUbNhgvlSWIkOqkhsQzKV5siWdFPRlLDuZqbND2RhTQzkLqv0Wg0NiOaoDQ2HXRaNYpHzYXJzdRWSADUtrh2DiQh10kxlNe8KBALzUY62Ep09BUxnFmfE68lYTGfCueYoI3jjP4xZX2uxDy12m+beBqNxmZFE5TGpkPmGpE0+F/thine9fPQpKKZRb8StRqSDslIJj7L0GU1IBINNTa5krFOr/qiGJ1j3dS4pFOtRKWzizYaja2CJiiNTQnDiU1vD0y6phYkiQamE51TXYtH5ArI/vc4I3y8ltfjI9HBBKR/S65orHZGbY5ERZLCcUQbGWm0o1YA3qrYKGRvM2XxbTTWEk1QGpsOGRGT6eOBjrK5Po8L/+E/Yp4TICnBH8W09B6rAyuEw3Bm19tRy+Jig/qdpOMu55MbxfPTlKR5yHuA4KjRaawOaXaTXOa2nQX7E1jN8817SH+knX1fjcZaoAlKY9PBUFzJSK4inFqP1JLk6sJqNZKoZPr6zJsioeEYVxJ2Zg7hUZOiQLRstS5qcywjV1vWBCSB2Sgz/l0R6VScoegK+J3drtubir8SnZ19P43GWqAJSmPTQQdZhD/EAiJiKDGkAc2FYcAcJzmpg7z/OdY0+B6X+zXbmHwNaKIxIodrc75+Jmp00v+EeiAsSfpminsJj4SosX2gvc8///zh61//+tgnWEvHBR7FFHlZi9WFpxZwJFsx/YQEgNtTNvf1rW99a+xrhKGvpL70O/oX70WjsZHQBKWx6aBAT5KgRsLBONfmAUbvaIIBqsgRZDq/aqoxX4lEQ0dbIHlRS2I0UK79o/nG6xr9o7bnSle60vhBm6IpKUlKz5BXDtru1FNPHV7ykpcMZ5555vgfYvDABz5wePjDH760pICC/cILLxw+/elPD3e9611HM59lTJlUplaTzm9/mwzQc4444ohxwclnPvOZc+uuWbDCbfTrt7zlLWN//Mu//Mulek6RlCRg9Lt/+qd/Gsn1/e53v6X61Xvz2zKn6rDctkZjpWiC0tiUYDZItlWEzkUXXbRkRpF0ZD4Uc5mQol4SoIkI8sB2TURG4hgCzLHMvl0xWa2KmhSQWW35TXl5LBoarqfGh4y1zIIveclLLjnobq+vwlYHz4mFHA899NCxLV/3uteNpOMjH/nI8PrXv3645S1vOeyzzz5Lx9PmkJPXvva1w41udKNxbaQU0JAKsgZTBsn56rUkpST747jLXe5y4/OsOPfcc8fFJTOTcQV1MUMxa0NxTdd6si9w/o9//ONtnLkB2rjvfe97434IL+dlRBjnvPe97x373T3ucY+l5IGUwz5IGn1+jz32WMrBk/cJsfnOd74zfpM3iGtk3280tgdNUBqbEgiNe93rXuPgf/bZZ48DaK4ojLlFwmJCNf1FzNyq5sTMsWpkcjbLwM9qxRKJ1LQAFwA0JT5lQ1CcvUJ0KAvBIEGREEmWOEZNDdgIPhO7GtReIeivcY1rjAIX7cljH/vYkRBKHiUXrGD9zne+c/ja1742fPjDHx6e8IQnLJmB0Di86U1vGr797W+PyfPYt++++y49I810aEfe9a53jQThFre4xfBHf/RH4/E18d9ygAw961nPGjMaf+ELXxhucIMbDE996lPHbMfzAHF40YteNJx88sljX771rW89POUpT9mGiJ1wwgnDpz71qbHfch/W79hjjx0OO+yw4Stf+crYJx/84AcPj3nMY8b3SmIO4Xv7298+kj3Kp01f9apXjW3RaKwFmqA0NiVygcA09wAIh+va1BlnRt+YJyVNNZKV1GxU7Uku5CcpogxIEUJM7UumyEf46cuiNmVK6wMWUbGvFypZsq39PUv9n6aq+nvqnCn/jSxv6ph6PgL+vve97/B3f/d3wze+8Y3h+te//nDzm998uNvd7jbsvvvu2+TP4RmqNWCfzs0I7Be84AXDrW51q/G8E088cXje8543vOIVrxiJj/XBlISwxjy01157jZqav/7rvx61NWpcMu+OjthTgOy8733vG253u9sNj3jEI4YPfOADwxvf+MbhhS984ZLGYwpHHnnkSG6e85znjP3q1a9+9fDRj3509LlxVW3qdu1rX3vsf9wngFRDbCDez372s4fzzjtvJGUQI7Qs4pvf/Obw1re+dbjpTW86tutnP/vZ0b+nCUpjrdAEpbHpkDZzNSZAPxQjcUxpj2D46U9/ukRE0m+FfXwzgLtasWWmnV+fFtX0hhqripfQmHOFjwsSMquXvOgHI9LZN+9LbARtSiULEpN5ZCH9IGo5uT9JjtopIDHMhRddDXoWaMsHPehBw/Wud73hE5/4xKg5+OAHPzhqIl7zmteM6xt5D5CT29zmNuOq1re97W2XfIUQ+mjkeK7nnHPOSADQkKBxweHW+n/mM58ZNSwQmNNOO23UZtDH2CZB8X6Xc4DmHtH2PP7xjx8OOuigkZSgmaE/cr9T57LtLne5y2haom4QJsgDZpvsM5AqPtQJ8wzbMTuhWaENOJ7rUP9TTjllJCg+n8tf/vIj2fnc5z43moIgKpCYRmOt0ASlsalhRla1HwgZBNluu+02khNmiWxncMa+z2BuvhOJQU2SponGfRmGDNSomHxNAYKQw06P0GAGSz3Yh+AiqiSz3Ep6QOZ00bdB4bSztSegEo2MPBISQwmYqzbbVuzHZGDbsx3SliHahlun5sElB2hPtCGQj1ngep/85CeH/ffff3juc587miyOPvro4aUvfelo0kA7kcTKZ55El2fF87nOda4zfkNK6EP0H4/VlMSzZoFHnjM+RWpjRGr55oF+RBmS6SRhs4gNbY1p6j3vec/Y16mfZsdEauj8pp25DqYgPmynz0NAUkPG/WG24hhMYZAmgMamI4Iaa4EmKI1NC2d6kghzllzlKlcZZ39qJUyaxsBL2KfbMiW9fiHmQJFEcAxOrmnqMXSY/eZGAQgnrs21MqKDujC7RfiZmt+MtwpzPlznjDPOGIUqQudhD3vYXBW/bQBWmwTMc20/CRf1wQEUYaZPD87Ikgrqyn59cIyesn2ody4xgNCVLLosAO2k74+ETj8P/lOGz5DjaJNZ4BgIEKaYe9/73sOTnvSkcWVoTDVvfvOblxaTTN+iSoK41t577z2aiu55z3sOBx544PgscKbVZAKoL8cdddRRw33uc5/R9wNHVLQn3GPFchoU+yVaGYgRmh/IQTUJ5TOmL6HtwfcFzQvmGEww+Vzz+piR3I7Zh7ZBq0J0ExoiTEy1r0GqiRwi+ufud7/78PKXv3z0kYEINkFprAWaoDQ2NdJcYy4UBIymmzwOh1oGalPWm8zNsFLX0XEmaiSQs36ElGYez89wYoST/i0KE47hmma21RSUhArhefrppw9f+tKXRpMBRACBcPDBBy8JxgyZVsuSJhE1GJq7IAwZtaSPjG3EcbSHuV/4r8bDdvBc/iOQdPTlP22MyYR71kQGQZO4cSwfn0H63IDUZKxFGKsmCXwlDj/88NFkgfYDgsF9YcZJXxZA1A1aNZxln/GMZ4z3ArnBn+SQQw4ZNWGQMEhAEhTaBVKC+ejJT37ySCZ4ZvijVCFPu0jC5tWd5/Lud797rC+/n/a0py21pW0lqWMbdb3hDW84+o7gNwM509cp2868KbQJZd/xjnccySIOs//wD/8wPPKRjxz7CpognInzXJ4n9/P85z9/vDbHQfxqVFOjsVo0QWlseugfApz5KzTNDssMFWdAfqfmRA2MZgYjdcz2arI3VeUKE7UOCg/2Ge6M8NZZlutSH/4z2EMIJBP4OpCvA4dOknChldB0AmFBcOILoVZBoiQpyuunWUSNRC6eSL0QTN4DwhmB7jHUjf1qfRBsEj1gVtx5Dq7VFCSqo+yOAgL9cY973Eic0EZgliCEGKGML0UFocc4wGb4L8L3la985ejDgmYB/w2cV9E45P1QHiHNxx9//Ej00Hzg01Kjse50pzsNN7nJTSbNL4L233PPPUdSxPPjeMwqWRbPE/Kl2ZBn9fSnP3044IADRgLM9ZOcCwjNH/zBH4waHwiIRAnTDfWl73EOpjO0f/l8qBM5V+iLaGzwk4EUzQqXbjRWiiYojU0NiYKaEAApcEZpFlm1HZoM9CvxHDUP6VuR6/morUifFKBmheMgImgtXFuHstjG9XS+5XyEwnHHHTc6JeKEmb4okiHKwc8B4YFQYpbObyODEDyaRMz1Qj2Afi65vk8uBTDlwJr/c/9y2o10cp2VOKyes6Og5gZBTgQOzxxBnlqtvGfIHyaOWkcE86Mf/eil5zF1T2yHpEAMknzV4yAby62ZowkLB1TCgL2XrBP3gNbGbeY9wSk4r1nrwLUhbJh1ch/9h2tB4GY5PLMNUsN1pqKqGo3tRROUxqZFDqz6dkBK0E6g1jcCRH8I0+Jn4jTzoPhbXwWFmrlMzAZr+LJaFI/Tl0HTjdobfU3UjiAwmI0jQAmDxXeAmTqkCnODZhhU+Jh5ECCLOFqutN3ye9b2RaKJqvDdWcJLnyJhJFU9Zhbxqlqg/J4iJ1Pbp8LD0xF3FnCOxZcFjda8OuZ/HcMXWTBw6phFzq/EZyNElDU2F5qgNDY1FAoSDgZQk6M50+QYNBKQBLUYkgzNPX4sT40J2/ytZqJmfc3kb/pvpC+H1wCSHD7MTm92s5uNx0KoqCOOlvgUKAzWmpysFhuhDtuDKmwX2T/vnhfVEi3SbmjHSIWfJp1FztveZ7IW99dobA+aoDQ2LRTiaijQfvDfqAxXNdZB1MX+dFzEhJLHuPAfphLs+tX5NnOhQDRMT64pBYLBb/0EzJWCOp19/Nd518UD+c8MGidFPoYlcz8QmMbmh2ZE0FqKxlZCE5TGpgZCnlTfZNAkmVSq2TO808gZZ6mahCQo+lJMaSxc4A+oETHsOLOTqjJXfV6z2HK8uVXUzphQDmdNHBW5dkaCtLDa/GhS0tiqaILS2NQgV8M73vGO4YILLtjG2bRmKwVqPzI/h5E66S9QU7hbVia8yqifzHnifs9LVLONJiBIimsHiRZYWwf9rBtbFU1QGpsamFlc5VUCkj4EmmWMYqnr3Uwtc79cqKyaGM/zmplVNkmM52edUtMi0ZkVpttoNBqbEU1QGpseNe16hstmJEYlAakpSXPQrIiOmvo9NSdJTvyf9UmtSiUxua9JSqPR2CpogtLYtJCYVHJSP5kLJMlBLggoptTtWcZUCGolI/6HvOR1PD5DVL12moha5d9obD3827/925Xe/va3n7Cz67GeaILS2LRQ+5DCPTUhqQUBmZOimnrMo1F9S0TNiaH/iMncsj5VM1PrbEiy5KpqgBqNxtbDz3/+8z2+973vXWdqPafNiiYojU2PKdNI1Z5IANJJVWKhxkNiUU09Hl9JzSxflfRJcZvH1zV1vG5uaw3K6mG0VtWcZY4RYHK9JIZEWM1L424SPuFq2GsN+0L6UzW2BkhJQMborYImKI2djkV8K2Zl9qyRODW6JjUmKWzUZFTzTGpMplaZredYZpqH8vysR61fNePoi6LWRfJTz691niprVhtWv5tsq6l23kwgd8w//uM/jtl5dZjmvln0j5T2rD/kc2Pto/e///2jg7W+RK5+bPbeSlZYn4cVjG1bymOtHhYYNDR8VmbWSpjdVs+BALFYIeWxjk+uEzX1TGf1jyxzVp+p78Kpp546tgGp/mf1k0Wz1zYai6AJSmOno2bmXERY5r663oumkVzBt5pIqpYjo2emHF6nCFStw9T21LL4P3OiVB+XWscprU2tQ+7LxQKtl3UwZDnXj0mhuCjJqfc2Ve+NRnSoE9l43/SmN43LBrCSsZoTEuBV4sl6SKzme+1rX3tMzEd7QkBe//rXj9tvetOb/lL5Rx555PChD31o2H///ceZLovovetd7xoXC3ziE5+4TT+YVUfNhybtU0tivcjr8+EPf3hcJ4hVlE0cWMlJlmmIOnWyj+d+3w/eFdrDRILZH84///zhz//8z4eHPvShw0Me8pBt+gxJBtE2cV49t9HYHjRBaex0VE3FPIIy5bTqfzKssm4NC/AxW2YwR0jk7LKaYcwO6755RGRq4E3B4Iza+/G/ZCQddqdmzFOzWvcjPFzfx2OzDL6533POOWe8fzPduk4Qdmtm3QjmPfbYY7znmiiu3m9t91n7lju3np+z+PWabfucuG9W733CE56wzbOrmVr5RlNw2GGHjSsY05a07Z/8yZ8Mn/zkJ8clCOr98bn5zW8+vOIVrxjT09O+7373u4cPfvCDo4aGbcuBxSGPOeaYcaVlrn/7299+XHAw+yDP87vf/e5ItiBdLBLIysO1LekHH//4x4cvf/nLI3G4xz3uMSb7c9FIy2MV72OPPXY48cQTx75xl7vcZVwo0Pah733qU58ay2FhQTQ3LBAIaWPZBTRNvHe/93u/NzzqUY/qDMeNNUMTlMa6YSrahYGfQTbXuVGYK8DS9JHHAbO2sh8V9Gc/+9lxxihYYC9NG6m58PwU+uk4K9GoYb55P6BG30w5tlbTSuY4mSI9miBcpPDcc88dZ/7O+skum1oSQM6Xo48+ehQWrv8j+M0MmrZGWNXZtNlrbYeaYM7/6fBrtt3clp9s89xv+zjjXg8kIaVt1CrwgbhNkVDujfZy5envfOc7Y3+i7SqSpLpSNORQ/yFXq54F63LEEUcMf/M3fzOSGcjKmWeeOTz/+c8fNSZ5LP2cPgFp/ad/+qfhLW95y0hkBM/r8MMPH97whjeMROeiiy4aTjjhhOGv/uqvRvJhe9BnXvva146aH87//Oc/P5qp3vOe9wy77777kjYOsxjHshYUbQLoZy95yUuGs88+e9h7773H61HvxzzmMa1BaawJmqA01gVTvhy5Ds5UdI2C0lTyqqNzlut5zArRoKA5SPKR2gzznOTMWQGq9kQBWn1Gqkmm5i1ZzhyjtiKjeCppSUIkWUKYAtfqkajxP+tJ+QhPhIgrMBvGzHmm3We/5UiCbN9sd75V/Ttrr34OCGGfJdtcLTrbwPpZF8kZ5+4IB9J5UMt06KGHDm984xvHuqBZQsgedNBB2zwHviEkd77zncffEpMDDzxwePCDHzzTjIEW4mlPe9pYLqads846a3j0ox89Cnvbexb0fUFj89SnPnWJvFUHXsBK129/+9tHkvC4xz1uOO6447YhKJCX9773vcNNbnKT4Q53uMP4brzqVa8azVRoUXx21A+/nDve8Y5jmbw/b3vb20YtEaYc7pNVn9E6fexjHxvue9/7jn41gPeWdoE8oZ255z3vOdzgBjdoctJYMzRBaawLUtAj+Fy8L00fSUIkFyC1HBIWBCbnM5vjmwE308HnrD7t7P63zFlOtLPqPyvhWz12attyPh6pefBaqUGyLRBKzGi5X8kd7YDwhYAkgZPgWA4kIhc1lDCkYy4w1FmNlRoTCUwlX2k+U+OQJIxr6FPh4onriTTxHHzwwaMw5T4gAWgU6rHUGefZJz/5yaOGBWEPYXn6058+XPnKV56sv4v6QU4gGfi2INhvd7vbLWvKsr3ufve7j2aTQw45ZIzWwOcD8w0kwboBTHVcQ/Od2jRBP4BsQJjwp+HZ4OAqUfKakCjexS9+8YvjcYB64+CbfYQJQPowgb322mt4ylOeMmpvnv3sZ4/78VPB1LPe5LOxOdEEpbEuUKAhRFURVwdNhZmDbaZ7VygimJllokFgENZBD2T+EE0hVXVfNSdet5KKrE+ta56fGo88rpKQlfrY1DId8Lkn7v+UU05ZuleFhpoTBS/l094SPolCCrMaclvbiLJzXaLqTJrEUSQB8hlo9kiz3XqTFO8fTQGRNdZ/qi5sQzNw17vedVxNmnPwP0HbcK1rXWsbs5DgPxqL5zznOaOpI+9/EWhuQgODxoNoHbQZ1OGAAw5YOo72gzAk6cnnBiA0kAwID/dK36DP4MBrX+J4SBifP/qjPxo1LbybaGM4LicGknz6k9uIcILgQE4wR0FUMBXd6173GstsNLYXTVAaOxw5uDFbc5Ve/QFUYWunV5C5P/02cHrF5q0mBSQhYPB1RWC/sx4eL3KWmPlOpoR2mpXSJDTlv5D/q5Yoj6mCH1QikPefCxKKJGOWzb0jpCRvzMaZaePkiKkiZ8KYfLJszTXVh8QcH3kP/pYcgjQNIUghS1VrslJyUgleEkgEJYtBQiS4v1mYavupukgQJWbcG6QE4sAHDQFmnnqOETC0da44vZJ7RMhDEDC5cF+UpfYkj8s+WB2mAVqe2972tqMjLc6tP/vZz0YnX/xbIFseh1kIh98Xv/jFo/+Svk46wnocfQbChgMvTrRocCgTzRKRTWhTIM5cM51wG43tQROUxg6DAykmGD65KnA1raQPh8IzSYjkBSGZfiXpq8L/y1/+8uOgaxkM9pKQOqDnddMnA8wyyaSPRr1XMRWVlESjanHSP6VqUKpPSvpx1Iy03geChDBYBLamG2bTzvr1bZGU6I9gG1dflNQyZF0q4fNYfVood4qcbE9/4kNfIvIEYYoGTVMf/g+zCIpkCQFK6PC8a1BXhDOCWIdY7odzn/SkJ42aO/tbAlMMPhm252rwyEc+cnxuaFAgQn/4h384kgFB2Xe7292WSCnP9QEPeMB47wnqTWgzZeEgy/Gai5LcYibCbEWbQEyudrWrDfvtt9/4PwkPxz32sY8dzUC0OfswBaEtIsKH9xJT2cMe9rAtlUissWPRBKWxQ6D2A6GHn4QzeX0VNN84S+U4j2E/A3GaFlL4AQdozvE4zkG1ft3rXnfUIDCInnHGGUuDrEI9zRFTWWBnkY8UyNU0VAlKlu051VyUGpNqEqo+C5plUpNiGyIc0k8FYYJQQ0hxnjPaJGiZG8bfuT9JomQwzUHpgOx+621uDr6nyNxKwXXQvF144YVjVAtCkj5FSCxklNk7gnpeRJDmE8KL5xEI+wJRKQjrjNhB8BJGqwawngdx4NypKJ/lYJ9Cu7HPPvssEciajZa63+9+9xuPZTv/ITFTjrSQdQgV8BlVUkU5EA2Ok1gadp/PjW33v//9x2N8t7gmIc6EVqdJr9FYK3RvamwXpswaDK6Yc9R21Nk/qNEdnuvApxDUB0IfCtTddYav86Xht2k7z7p5vFqFKSfXqi3xvEoiUnuRhMX/1QnXdppyfM0yvc+MrPFYzSgIZma7EhPbB80J989+fVDUXiQRs962g3XMVO4ZOaWfy5Rwyz6gMPUZVNI1q/9U+IwwIZAgDNMB4a1oAnD0JEEZgjzNKIuQINtouWPV/lRTBedJPmoZ/Ddh2mohOeCTZKuapbyO7U6dpoh1NduJKTIsaZvSjAnrlmXYL/PctdCWNRqgCUpju5CDkRkwDXUFDl46vzr78ni1Ih7nLD3NMpkADVU2QobyGai9jiYMnRNzkK2+FJlALe8hNQPVBJWDbxXMU0LW69VcKklmZmlgPE5iRJuoUeI4NAY4IabDoo6TZvL03CRWSQ4lL96r5ELCkveQs+LqvOtvTTmzyOEspECjf9B3MN2QqAxzCeCZYj5AW7Lbbrut+Bq1XbfnuHnnr4VgXqSMqXtfSX2nyNVq67Do9kZjNWiC0lgTqDmRMDgjU62sU6zJvaqJREHncc7McsYPyMGA+cJEWApthWs6EPIbtTzX1xRUUU0wkqbqdJh5Uar2J0OYQdW2VC1OXi/35zU1sWjGMXTXdsHhVVt/1sMoHcNCJTpsk+gASWH6rmQdKwlL7U+9D8nRSoWT7Y1PA2SEkFiICfVmvRscRclKCvms0TC2X617o9HYPGiC0lgzGEqK4EzzSc6483tKoE0Jbf8jzCQ31aHUY3M2jvBK+/3U9avfRSUbHjdFVNQKZfnVsTSR5SSZqmQtSYMaJxObZcKzJEJ5XY5D7a8vQdZvXpunI+wsX5xKXPLeajlZdj5T/EfwJyFdO9E3RKvg6EqODvwrIKGaYmZpqESTk0Zj86IJSmNNkMJ3OUwJ7kWOTWGeYb61rHTazG2z7OvVxDLr+OqrMuW7MhVK7PlqOep9pyagXs/IJ/1N3DdVx1qXKrxnCfPU3OSnYp5JodahEi/uG78ZNCRf+tKXRlKCuYZoEaJjCIsl4mSqjm1OaDS2JpqgNHYZKORruHDNA6GZBtRkVmDKSRBk7pG6Bs0UprQXSVwqialp+tN04vH5P1GdZr3/em+1botgEV+GRctIfx9IFUSEkGAyleLsimaH8FkSiOHMi7ZtLSJ9Go3G5kMTlMYugyQolRykWaFGLnieRCYTvIFqjsoIljxuVp0WIQe1vkCfkWpWqQTG/aaLzzDmKQ1TRm+sJ8x5Q0Iwom7ILsqKupjOICMm/4KkLOK82Wg0tjaaoDR2OmY5lNb//CZaJDUMUzN3/2cEkP/znGomqb4p9diagC3rX8nMLGFbj5vluCsp8Tf3jWPsLP8QkJqlTDi3EtSypyKAsp4eQ2Ixsvzi6MpyBIQDsygdicH4jaakCUij0VgJmqA0dhkgeA2jrajkBKSpJx1iDUOuJpYpzUsmhhPLaVSsQ3XeTd8ZyYfaGs9NspROwHybi2SW1ibvaXswTwMEXOyRHCUsO4DphoXpCPPGwZW1WNSUdOKuRqOxWvTo0dgUmBftkeYVfxv+jBPqlNNuOrtWE9IsX5aqeagJ4aa0Q/Wc9FPJkOe6Wu08zNKwrOT8rKP/Cesm6gZNCeu7sKoy+VhYIG/fffcdo3AgkB1Z02g01gJNUBrrjtU6dM4jIFWo1gyuuS8XBZRETGkuqvllFiHJ7yQ06XSb32l2Sgff1JjU0OzUukzVI6/rebNIW91eCVf+x9EVX5KTTjppdHTl/1WucpXhhje84XDwwQePmhJCgmuW2Uaj0dheNEFp7JJIIZummoxwycUGgcnJNPFUR9S6snElGdVXRdTQ4Kxj/s78KtUcMxW5kzCvS9XmLIcMX651yPpbb66DuQYn16985Sujw6vr3pA4jXWOWOvHxHiNRqOxo9AEpbFpMOX8monaZuXYqBqMJA6rcTJdpG5iijDkMZIpiMOiUUVVi4JphkX2WDyOT+6ThJHNlXBgcpScddZZY3gwx+6///7jujd77rnn0ro+88xpjUajsVZogtLYUFhUOzArcqYKz6oFAWpHUrOQx02t5WNZU/XwuEweN3XsVEbdmgMlz63Os4ugkhPu9eSTTx4OPfTQ0SzzjGc8Y2lxOTQjrHtz7LHHjgQGMsfKtkTesJIvBAXH17oYXLZ5o9Fo7Cg0QWmsO2Y5pfp70dl5aj+qs6llVF+U1JSkI2xG/FRzy5RZpWpc8tipelpu+mrkfWpaqvWbIlzzfHiyTkTaHHXUUcOLX/ziMfQXx1ZMNfvtt99wxhlnDKeccsqYp2TvvfceHvzgB4/mG8OBZxGQJiaNRmO90ASlsUuiOoFOOXimY2meB9SSZJhvLT/LS5KSGpep+qSzq6j5Q7J+rr2TJKWamfKzCMhL8tGPfnQ47LDDxjBgwErBr3vd64Z99tlnuOUtbznc7W53G6561auOpAWtSmqOGo1GY2ejCUpjQ2Clfg0SgCkNQ8KIGMkAqM6mGV0zpa2oSduqySiPTYKUJGVK81EJR4YV5/WmfGTmAdPNO9/5zuFNb3rTGBacGiX8TH73d393eO5znzumnK+J31pD0mg0NgoWJyj/+ePhmGfdeXjgP91p+Mfj/2a4zX/dgbVqbGqk0K/bF9kGZmVUTV+QGrZbtRwShKlQX8uqv6d8RUTWJzU3uT01PhxjmDOYShhXTVXLEQgicN74xjcOb3nLW4Z//dd/HX7zN3/zl86BpLz73e8eDjnkkNGkk9dsNBqNjYLFCcqv7Dbc4cUfHt7wk7sPz/ybBwzHvOCA4bd2YMUamxuz/Ee2F1OajSlTTNZBzUXNW5IEZJafSSUeIAmRRIRrZKr8zCibodCznFBxVM3FEWcB7QnJ0x796EcvkSSTvGXiOZKquVJya00ajcZGxMpMPP9lj+E+h5023GcHVaaxdbCWJoVZppCqpfF/5jqpi/SldmTKmbf6vEwRirq6cq2jRCGddPNabIeQpDbIcpfTdLDuDQ6vGaXkdWsdMzqn0Wg0NhraB6Wx0zAvGqXuXy68dSqSBehXkuaTXF8nU8j7vzqkVtNP1mWKzOT1MhonF/BLUsL2ukJztgH/0XbUtYWm4HpFXruGNvu7fU4ajcZGRxOUxobBIsJylkZATPmTzArD9Zp1jR4JhGYZj6ualllIcjLvvqZ8VKbKqU66ec7UeVPXXQnZmyprqpxGo9HYkWiC0tglsJIon0oiNI0o6DVtVKdWTT4Z/lvNLB4LZvm2TEFNSqbZt6617padocfWL1dinnWdWlaj0WjsimiC0thlMMs3JFFJh6aTJBOpmVB7Amkx1NhFBKc0JqmBmRc6PGttnWoqmipLYiKRykUNV0LSVrNv6thFr9loNBpriSYojR2GHTGbnzJzzDpuVoix+3OfTqOmwa/HTYUKz1pdeCoCKMlHhiBndtlZYctT15gVwrxIO6/0WbQmptFo7Aw0QWnsUpgVmpz/U2tStQ5JOPKjhsJzM8PrLGfemuvEes3K8VIJkeW7PyNvUsuS11mJFqXRaDR2ZTRBaewyqIJ7uXwkNWdIml8kDBKDjOap15vn7zHlhOu1prLIpnmpRgVVbUrWfSp0uTEfK3EGbjQaGw9NUBo7DMs5ja70nFn7l/NLSd+V1FRUnxY1LjXcOFcpzutVglFXH65anamQ36xfmnI4NsOPZ5mIanlb3Ul2qi1qxFM+i10RqR1ci2e8aKRWvkM74rod/t6oaILSWHespYliapCrJhaFvYOeDrFqTRxwp0iLZZrHJE0yU+G/STKqgMzja4K4eSsX57a1EkqbFbTVf/zHfwznnnvucP7554//r3jFKw7XvOY1h9/4jd8Yj9mVyQkgJw4rVV/iEpfY7v5A+3z3u98dLrzwwuEmN7nJNqttJ+ifX/3qV4df//VfH9dwAmvVDyn7M5/5zJhk8DrXuc7MOjS2HpqgNHZZSEYyLNhtNQKnRs7kIoIeP6UVmfJtARmGPKtuU/uqKap+198I1VkmqMYvg7WIPvShDw0f/OAHx9WbEeYI1cc85jHDve997zGJ3a5uJjvnnHOGj33sY+M9uZbSakG/+vjHPz68973vHT784Q/PJAf//u//PrziFa8Yl1H4q7/6qzUlETyjv/3bvx1X2H7qU5/aBKWxhCYojXXHLPMEqFqJWQ6qub+G6c4iASBnnOknUpOrVWfUqt6ux0/d15Rzbl6rEqk8r0YIzSNDVeszKwR6K+D4448fXvWqVw0PetCDhnvc4x6jNoWFE1//+tcP++6777DPPvuMx1WTHxqJH/3oR+NKz7vtttsvtR3RXZLE73//++MijBznkgTZJzj2e9/73ljmla50peGSl7zkNmVxHAKfdZN+/vOfD3vuueeSdo5zf/jDH44ajctf/vKj9ie1f+w/+eSTh/e9733Dfe5zn5GgeC+Uh+aIMq9xjWuM1831l6bgeT/+8Y9HjdMPfvCDsT58ar908Un/U1/a7Etf+tJYrxve8IZjfVNDxXEQkNNOO20444wzhqtf/erD/vvvPxLF7N+/+MUvxnrwnzpwTr33xtZDE5TGhsSiAnYqmmfKzDJLmzLr/NTMZIRP+qNY1iyfhilzzZQz71Q90wdlKsx5Nb46WwFHHnnkKAQf8YhHjAKOtnrmM585HHvssaNJpBJcBf4rX/nK4eyzzx4F/h//8R8Pd7vb3cbjBZqZJz/5yeOz+OY3vzl+P/ShDx3+8A//cBTakpOf/OQnw1vf+tbh8MMPH8nRHnvsMfzFX/zFcPOb33ypLATws571rJHEgDe/+c3DVa5ylfF4VqL+wAc+MFx00UXDZS972XHRx/vd737D7/zO7yyV/6Y3vWn48pe/PB77whe+cNxO3dFCnHDCCWN/xVTypCc9abjtbW+7UF+gTmhk+Oa+X/rSl451RvsE7I+Ca3z6058eXvKSl4wkhf9XvvKVh5e//OXD9a53vaXjIGJveMMbxnuE/P30pz8dHvvYx46f3/7t397mfeTYT3ziE8PrXve64b73ve/4DNOvq7H10ASlse6Y0i6Ief4B8wR8Pc79DqpJLCpBqXXJc6xTjcqpDrdT4cx5jSQz1Wel3l/ViMwzO02hRgBtFXDfX//610dTQWotEJwPechDxt+1bb/zne8ML37xi0fhCWnAz+JFL3rRcJnLXGY46KCDlspFAENybnrTmw5PfOITh4985CMjQXjYwx62ZIYD+FL8wz/8w/CUpzxlLOOYY44ZPve5z43C3r7ws5/9bNQ63OpWtxoe8IAHjJoY+gXb0P7c9a53HW5961sPn//854e/+7u/G25wgxsMN7rRjcbyIVB3vvOdR6LCt/WDmEG0Hv7whw+XvvSlR5Lz6le/eqyv5GYK9mvMYb//+78/HHDAAaN5jHqgbcKkU9uYc9AOYRbiWpAkzTRvf/vbhxe84AVL/j6nn376SE4e9ahHDXe5y11GYgUxg4xlvWjfo446ajRd/cEf/MGoHZIcNTnZumiC0tgwWFRrMo+czDLRJKZMJ3ndXIPHspJYVG1HbluOREwREuvhKsbW3cUBk9jMM99UM9EiRGazDf60HYIvtWAAAQrxzAUbuf8zzzxz/GACQttwpzvdaRS8aEkkAIIZP4SC2T0miRNPPHEbkyTP69vf/vao+WD2z7bb3/72S6aL1IxBNCAEt7vd7ZbqgjDHzALJgShhUsGBFdIlQcE0gikFsnTd6153qdwvfOELw3nnnTcSE/5jIkITAhninHl+HbbZf/tv/20kJJCHQw45ZDRlJUHJvgJBgWhgSoMEUQbtARlD27T77ruPx1EGmhHuFc0Wzsr853rVZIoJiHY5+OCDxzZMv7DN1k8bi6EJSmOnYJ6AnYeqffG86hzLgFwX+/Obj6ns8/ypsqecVyUQ6YdSnXLr8VnXKTNRPdfj1IZUH5NZbbcSkrfRB/5se54ls3xm1Wg7ZrXBta997eFrX/vaKJgRrpSBtuHd7373cItb3GK48Y1vvM25hpMrMCk/27L6LHEcJBKykho2nxX1xOSTSyhgNkFLwnbL5DpoeVJbx7loJCBAV73qVUcSRN2pc20X9tX+svfee48aHQgJPiVeYzmfJN8X3wl8WFJj6DEAoudz4X54JpJriA3XdIkG4P1h2uEYiM1JJ500Ei58bPIdQctEu6KRQauFia6xtdEEpbHTsRohWQX7LIGbPiJTRCS1KXUgnzLJeFySIjA1mGcd0rfE46fKRki5P2eXDP6z1vfZjEgNF/4Yp5566jjDRsOByWNWn8G8g3DD5IG5A4FKdAp+EJAXkEIdZ1LIA2YNTDJf/OIXR+GPcJy6xqxn4LNFc4AWBXPFXnvtNWo60CxQJ8Jo8/6qNo3jJTmE/OLwi5kH7UMCoY+gRztB3cH1r3/90USEBuJa17rW8La3ve2XlnmYBe4JUoIz8R3ucIdRC0NbZX2tM/0QoJ3BkRaTDpoR2uyjH/3oaJ5K3x00JpAk2v+BD3zgqOk5+uijRx8XCIqA7OC7gmkHvx7qgP8NZKuxddEEpbHTMcsfZTnUxGdTgzGDeR5XtRdVO1Hr4/8pzUjVyiRhqfdStTxT19FMkCTGczJCZK1yoWxE7Qn3C6lgxo2g/8pXvjKaEhCWCE8E3jz/mjve8Y5jxMhrXvOa4ZOf/ORYFuVgmrnZzW72Sxl5cSYltPXQQw8d/UU4HmKDf0j2Jc671KUutRTFwjfajmxDjsEshHnmuc997lI9H//4x49EwvLwz+BcfSwE18RB94gjjhh9MTj+wAMP/CVNApFBkICXvexlo1MqvxHsmKr4zzUQ7I973OOW6jvrWVNHiBnk6LOf/ex4be4TQkUdBe8RDr/2XzRJj3zkI8fn9N//+38f90OM8DVJcxLkhf34tNAmnAdRudrVrrZ0DHVDY8Q2tEX4AkHq0DyxvbF10QSlse6Y0jBM/Z46dtZ5SRamnHAR7IaE5vZKNtJ3Jc0rsxxk87qz7k0tiPs9hvok+ag2eWCYZYazTvnArBaLOt6uFaY0V5IwZvGQCRwpcV5FyKItufvd7z6aa6pAnwLC+8///M9HB9dTTjllJAMQBMwHmIa8tmA/UTKYR8gvAhlASGY4LR9IAMIfQsP5+F2QFyR9Kbz+8573vJEwEC6MgEUzQN0tCy3Ls5/97CWNjnXSUZf6fOtb3xpJA4SsOrnie4IDLL4enCM5gGTRbpiF0AzVkN8psJ+2wiGW4zmXtuaT51L/pz3taeN7JOlHy4MTLxou/uM3UvOyWD6hxZjdMOFQtskSuW/aGhLDN/eK/w5+KLT5RiTRjfVDE5TGLo8pDUh+FPLpo1K1EGlucU2cJAT85xs7fdXCgKnvNOOkMJ7n81JNRbXua4Ws00qwWm3X1LU1GeAciikDgUu4LUIeksCMHSG1klwYHMc5aDIwB80ijgnaHBMJRKL6XgiIDD4sloMwr2YgfyNkM6y4hsoi7NXmTF0HsgAJmQXON5Q37w9TCvfh/0XajGPQ7kAuvK9Z4LnUc2nrNOlMlQ8o32vUfUCnWu+vHtvYmmiC0tgUmBqMUxuRWhC+9fVIJGGowjsJQtXSVDV/JSRTjq7VHFWjdNJ/gH3p1LuzMKWZWil0lGSmjykGcwiCdb/99hu1JZpRpjRWi6CSxkVXf15OoFc/p3kEb7m6Tl2rEth55aX2bsqXZaXkc6qc1WC9tXGNzY8mKI1dHjkg1kFyyl+k+onkYJ/lVBNOFX6V0CQJAtXfpJ7vx3DiWh/rmvVN7c6stlhEOK2G7CwqeKbKxreD0NezzjprDJvF/AEZIdsrGV4xDSSZmNJMLHrt5cxuFcu12by2nlfeLNK83DnLEYZZbVP75KKofW/WPSyqkWk01gpNUBo7DIsOlFMEY155dZY4a1Cuvh3moEBY1ggaM8ZO1SPNQVlWZpbN+5jSwmgmqvWbMhOls20VGHUV20Vm3FP3NA/ztCTzyq73D2hTSAlRLWQ7xTeCPB58o9bXL2Sl15uF1RKblZKB1Za36DnLaXPW8rp53mrvd3uu3WjMQhOUxqaCg6Rko5oK0FakX0o1nXh+RstUvxFRo4g8f0pLI7KMGpEjAanEKWfW1dF3I8F7JhEX6c9xeCUaBW3JbW5zmzFHB1qTdJBsNBqNWWiC0tiwmCfAqjagkgDJg9lDkzSk+WZqjZ1MvDWLnOT5+rNM2f9TQ5Lko4Y/13rkSsv1mou2UcUi5p8pZ96pe6qgDSAl3/jGN0a/EkgJUTgQE3xLyHlh+vMmJ41GYxE0QWnsMGyvmntq35TTZGog6r66mmv6daQAnnKknYoAynpU4jJldqnESGKSpMXjkvCkScdja7K5qbZajkgsYv6x/GpSy30JspaSP4M05/iSkIuEDyacXFF3uTo0Go1GoglKY5fHlFBWkGrCqaRBIjIVeuzvqj3IqJopopCalxouXIlRrlKcJMUygOQIwpJRR4toQrYHmb2VXBeEfOb9sLYMGhLCg/noW0KSMcJfO/tno9FYCzRBaWwKzNIopClFwZ7mFPObeGzVHCTZ8Jy6PkuSmalstrOiM6pTaV17J81M+s7saPMI5RNtc9hhh40r9t7//vcfU49DUshTgvkG4oI5B38SEpyRWIycJZpwKlpj0mg0VoMmKI0Ng+WE71QIqv9n+aCkRiQJQv6vuTKmTDZ5Lf5nZlCP0em1ZqOtPi+17hIjnWAzmqhqU5Zrs9WSAckQmUTf+ta3Du9617tG082b3/zm8dokUGOtF1bYJYna7W9/+zF7qZlMG41GY63RBKWxIbAjTBZTgjs1Kq4gW/1JKtnxW/IxKz19hgG7LzUghjmnT0tqUxT0phMH6YSbpqVFVjheFJbDmjekUGflXyJxqAOr1ZLSHU3Jk570pHFtGEODl0uj3mg0GtuDJiiNTY1qWqlhyJKFSmaSLID0DQFJLnJF49TeVMLitjw/nXStn2vOZBgy26aIU9UerRaYbDDrQE7I9Jp+LtQN8vK1r31tuN3tbtcmm0ajsS5ogtLYEFhLoZdl4RfB2ihoBET1E8kw4TzGfQpqzC8QlyQTOrCmZsNFAEGSGuD5IH1fkhAZ7WO5rI/CMvaLLJaX5dY2naWlQkuCSeeDH/zg+J+1Wbw+7Wfq+WOPPXY071CX1p40Go0djSYojU0LBDRRJaxu+4tf/GKJWGhmYaG6JB9JRkD6fUg+ZuUxMWIIINRryHGSkaxf5j3x+DwOUsKS9SxFv8iieasxlUHecHJ94hOfOEbgXOEKV1giJZhzLn3pS4+r0FJXzTudy6TRaOxoNEFp7DKYMnEsBwTvve51r18Kza2p7es1auK29FWZitapZqIMI65kZSp/SiU7bq8ft6+lz87lLne5cXl7ITmaRUJ2dJhzo9FogCYoWwjzolMSqxFAG3k2reYhc5hoihFTa9ykP0mN9KkhyBmJ4/npyDqVq2VWm03lV8l987CSZ5f1WI6ITPnxrBV0Vk7UNpgibunPA2pWX7/TRyhzzuS5U/ecdcn7zjJm1XGqntXnaOoatU72VTRbG/kdazR2BJqgbELkbN7BjuRaODrib5Cz+4xOYRE9/RyMMlHwZiZV11JxP2r/K1/5yqNZYEcIsOUwJSQy6VptD/eln4ckpgqUxNT/eo7IMOf6PUVW6r3UdlyO1Myr53LbFz1n1u/tAe1/3nnnDd/5zneWfF4wvfEbDZd91f+GeGuSc+FH/XgwV9mG9Ed+63+ELxKmPsB1LENTn+8E29hnP+G6mvT45l3yneFc6uN2I7CsN/ssj+2UxbWpN7AvWC+OZx/HcT7HXulKVxr222+/JUfpJiqNrYImKJsQ1Z/h+9///nD88ccP3/zmN8c8FgyAJtVKIe7gmQnCXJwuTR4M/AzMHM/Mbs899xwdJ9P3Yj2xqODMCJl6/FR+kkWwSJjvSrQPW034ILxZVPDEE09cEuoKZwmIgt3+yDPkP30QcEy2sWVICvyfywzoY0NZP/vZz5bMfRIdSQZ9mmN8P6wbZUN8uDYffHSIfuI8iUQSZ46nrHSiTuIssaJe3DdlQfwxUSZZat+fxlZCE5RNCMkF2hIWbzvppJOGb33rW0sDIgMgWUEBgyD/2edsj9mcCcP4RhAw8Doj5b+zPAdSfu+sAXRK6zGPOMzSTKwmp0iaIub5yFQfknnHzdq3GcH90pfoqyDDuul77KOPSQJsR/uvmj+FOP3Qfkz7SV5yGQJ9bH7+858vaWk4BgKhFkdtCtcmiy7XhshwDu+B5ESi4vFsowy0NdZB0sG59hdJjPWS7BsVxuKKOEbzbvFZiQat0dgsaIKySZCCksHu/PPPH2elZ5555pLwdTCGYEBCjMhgO4Oog3yGujojZOBF+0JZDNaAgbz6BmgO8r+YN7DOM3nMwixBXv0A5p2XdZ7yO1iuTislGov4j8yqw7zjFsVq2nlHQ5MKQp4+qHYuE9vRV9PshSBH2AP6JecANSr2c0wulgk053Et+rKamEyKB7helsm12KYpiPM1C7KP6xiOrSZGIu9v3yHJv/5P1InznRDwTkKIIChqedL/aaM8t0ZjPdAEZZPAAYxZHinJv/CFL4wkxVDRHFz5hmToX8JAyADL4JmCwVks+0l7ngvvacNfVPiuJ1bjg7GaY1fijLqa9plVh7XQUm0kU0GacuxXaC7sZ5o39E8xZJzjWT2ZY9lHn5YUSAjSh8X+zD7eA69FOWoJuY7vAddHE1IdpA25zmM5X3Oo19VEBInhnHxXPNd7Zj/5Z/Tl8jgnFhvpeTUa64UmKJsADF7Mwi644ILRnANBYQBmIGZwlZSko5++GGpB0saemhBnqPpvpHragZcZbZIVsDMH01lakZWWIWaVs6OFxlYx90hENGVobgSaZSABmIHon5pU1AbS9zWXAE0vmkw4Ts1MmiHts5IX9lu25EHyUddEou9LUtR+qAkCvmeafFKbo5nV+ybPDL4ml7zkJbdJkJflbObn32jMQhOUXQizQiJ/+MMfDieffPK40qzqZ2d5qsclH5ahGhw4y3TwzQFRvxN9A9jnTDHLmYqk2dkzvkXt9lNmn5WUvx5YrY/MWpexvZgStJILSYFaktRGQDYkBPk/o69Aakr0P5F06zfFeTqqSj6MqtFMk7lgIBfCcnM17DTZAOsmOdF8yjupxgZASDDn8IGcaWIF1oey0ul9Z79TjcZ6ognKLgx9TT72sY8NZ5xxxjYzRVTTzuDYro3fmVnOBNNxz2yhCgo1KarOneE50OrUl0nPliMG8/w9VnLePCzqA+KgXwnWcmUtguqfM1Verd9y0UDbi40g4PJ+iTBD86czNlDDkHWVDKS2QzJtmK9rCEmwU0shMWEbQt+FECkH4sAxkg2jhVJ7A0nhOLWHlJFh0Jqf2O7SCl5PB3NNWZSBjwnhwzqYp/8M4Bjf1+xHTVIaWwlNUHYhOHtkoCOnyWmnnTYu4MZvTTh8a9ZxZmeOBU0xDvCq0i3TWSvnGk7pYK2GxZmh4Zc5Q9ye+0rsCFPRcpqDRZ14dzQ2iplsESxKLOsx9CGIyZe//OXhlFNOGSNyJARqPDKsHSFuX6SP4ndCHzTUXTMOx+i/YTn2WYmNIbySF98RI4DSzKnZU7NMalm4tmHK+pGoMeGcXFoBWA73wlICRgalVkvNjuX5PmuibTS2Gpqg7EIwMoDQYRZuY+bpzBI4s+M4NCPOQlVbm6fBQdG8Jc4SM7SYciQxluEg78xOUiMBygG5aiWsv5ilrVgJ5jmfLjrTVAjOq8dqSMM8QjSvzvPquRZYSxPPSsrwedh/P/vZz475T+in+krRryQFau4yD4/akir8PV+S7DOVRGs+UtNhojWJgGVLMICaFMmB7wTIPEG+N5QvsZHkqD3R0Rdigq9JXRhSPxYT0Pk+ZbLBJiiNrYgmKBsckgy+DR0+55xzhosuumhpQM407aqajSrIlXIzG6w2dKBwMKRRzYg+LA7QfENyUGF7nupzB/ZZPgZVyKegXEk0jHWfIj61rEVJynLXnyJbOwo78hqraZvVXsfybTv6CJFgp59++nDqqacOF1544TbhtRLj1FKozaMPappMZ9f005BIGI0GNAmlKUaCIyGQsIDMSaKpyHwmRhlxDX1Z0jSqycdroeWRFF3iEpcYicllLnOZJZNNJoPzvVVLZD102OX8TNTWaGwVNEHZBfCTn/xk+OIXvziccMIJo0Os5MMZpoMXA6fmGdN45/ojZuQ0xDhnaA7CU4mjMsW4dnhns9rK01FxESQ52h6kMJwSwMtpDFaiadneei5XVm2LtdbqrBeq7wikFnPk5z//+bH/qt2jr0IA1Ozph0G/46P5MRd2pP/pV6WgV/NgvwUIfHxMNKNIoM2WrPbPCYAmm7pEATBkGRgC7b3pz1L9XrgvzDmXutSlRnKiedX31X4nSZHE+Q6CqWe80Z51o7Ej0QRlA4OB69xzz12K0GHAdVBmcGWg1/s/VdKacTJtePqlOEM0QoCyUhVuoiwHSM+RjIAcXHORvUUdSldDTKbIxEq1L6vxm/C41c5e08lx3jVX4gi52vtYL1g/tCb4mRx33HFLa9VIImzTqZWf9ReRHNiG6VCqWScdvO3jIE0+QKdvP5wP2dCMZBlqWbyGBCd9ToDZb40WSvMUWg9Wieb91OyaTuVqJdUGWY7vtvmHct2rtTTPNRq7ApqgbBCk2YLfaE1ItsYaOgyiDmQOsuROYMA3L4RkQ2LiIFsHxEzB7axQjQtQaOjvoqYlZ7NqTLKMeh9JWsSis/5ZAnqKBKVg87uagOq1Z9XB86ogqCakKbKTTp1T+7Nd57XDlHlkCssRvEXJ1EpJ1yLOxPpAsQDgMcccM5omNXdIOpLcqu1Lk6UOsOn47XH04Vxsz3bifUjfFf0/JOSUqfOpfif6ouS2jN5J/y76ve8B76QrDOPkCyHhN3VDY0KUjj5e3of3qPZQ0l/7hpOHdO5dqYay0dgMaIKyQeDgw8CO8+BRRx01rvL6ox/9aElL4nEO2g5szjIZHCUWAOKS6exVazsQa3t3RmuuBo/VMTAHT/1StJnrSFsF3ZQgTwKmKakOvLPOSeFXy06BvhJM1bGaiepv2yDrO8/3pZKeKeI2q255zZWcV+uwHsj+ASHBHInWj/5r/dOHQ5Ok37lqtlEwuUigeX1qv1QjY1lG6dhHXeG4htdn1JkOrjqC64Ol6UiSwfuS4fbUwbBhPhATPtRV7aUamQyHliz5HgDvW7Lk+fqCNRpbEU1QNhAc2Fl12DT1OgUCHVbNnQCZcbE0jksVcl1VFTjQGbnAQG4OCM06ZvBk8PV6KWS9hmr3HGznCfuKWfuqQJ8iPpUMpO2/EpWqGp+1z/2SrSkNxRShqmVYzlQ9QU2bnvtmaX2mylsOi5gDZml0lmsjUduI/sTaT/RhtCdmVZXM+ozMlJqL/3kNSQFr5eBoaj8ESUTYD9Jh236fGj/qBLGQRBiJA9KXS4KfqxXnCsdAMmT5fhOdc5WrXGUMHZYIeZ4aGbU4huXbdlnnzMFC20msVvrsG43NgiYo64RZM1oGLwbbr3/968MnP/nJ0YmQwZLBWU0Htm5DIB2gdbpTBcwHVbODvrMvB1nt/0DbNmt/6MviAoA6L1o++6kfJiVnk2arVch4Xi6OBhQ+U5lmpzQe6RuQ5pT8ntKsKPScXaepq6rO67mJdMa0fllGXi/vo4ZX1+c9y1QzVU6aNKbuP1GvVQlROn1OtUO9fp6fRGpKA2bbuJ+oHJZZOPvss0e/E/obfci+ZnbYzLwKIXChPQU4/V5H1tSqUKZRNRIDhbnER5Liwn1qCNmnOQXCInlRk8KxEvXUJhqlpl9Irj+VocN8OF+HW4lImjo19/huZj/T94tjjEbKBHBTfbXR2ApogrKOqAKEwQgnWKIb0JrkrDAd6DJSIWdxDIqSiYwoyAyaZpclrXZmhnXQdjFB1ecOotTF84HCifI5PpNjQYxw5EW4GA3hvTrAZvSC6wRJmJKs5GKF3q+aHQmQeV28lmYnf9teHie5c7aqf4JlZspyyRdQUPptyKvtbRio5gaFIHBG7ArQucqtAlbzhXWjnhLDTJfufbtWjYvj2XYKW/qN5gpg1JX37wJ8htiqQUjh7jUlB2rXkjBAaLmeJIHrYY78wQ9+sOS3lP4XfPt86CO0iedluK9tYPt5rZpVNn2sjFwzeaDtluvn2I+sm/0+CaTvjhpJ66cDOZBE8MHHBNIuuVFbYhvlshHeJx/XDbJMr5GayvTRsU6NxlZEE5R1QtUA4ATLjJNsmqxArHCVPDjAOghrM1eQOpAz8JpzAWTOBwdgs1yq8VArAnKhPxNlcaxmo+pA66DvyrGQE+pAfhYddlN41iRc3p9CJNdScUDP9UokLGnGUUuEwE2VP8eZ4h/YBkY2Gc7qoO8qz94vjo65cqwzX4mdglVyodOkM2CJDGVRR8pH++Usme389zlIADiX7ZJMytWZmX30D8pA48U1qAfHSZoU8hIBn79l+dxcbE8hq6CWYBm+S/k+X+5BgSuJTS2MREwSZLtZH+A++5Falcz7IWGSpNk3892RlOq34nui74ZmnIy8yeRuabKxD6TZyWebZMj3yvtgPysO77777r+0oJ/9TPJtf05tXJINyYmRcZm3yDD/aqpdT7+ixvrg4r70gwMOOOBfrnrVq3511jF77bXXJS5+/7acvN5yN7wzofYAbcnnPve5UR3u4J7mBQdeZ6g63RmdoEBycHc7UAvg+QoBk2IZ+SNJUB2uSciB3/BIB1mQphqFtKQkU4lbDwZftSXMhJ1ZAwWIBCMdF9OsIqlIh0IFKvfiPZgJVIEpeUnVe2oqXASRMjKluD4/OhgrtCEJnqe5zGfAdgVZrpiLoE8NlMRAAU2buA/kWjBqXmwftQnptKkvA9fkt2vLqMnRj0JzRIbBAkmDpg8JkSaNDCv3Psz8qu+GzzSdPiXBkmK2Q7gkVPYn+5yk0lwoKcxzRWKPty0zEZokPglTmpOoc/Z9y1cjZn18/yxHcsAHUoKvyRWveMVtiLMfiYmEzjb3GeoDwz3a3rZtdZi1Xa1/E5PNi4MOOugfjjnmmKvd+MY3vnDWMRf33d0u7j+/cvE4dI31rNvORhOUdQKDDv4lX/nKV8b1c9CgYHZxZg2MxslQXrer/nXQd9Zm0igHsxywHQDTZg8shwGZOhi5o5+AqewlGZIniZPmJ/4zqwdqAyhXwe5A7QCr34EDu9slC/62jmlOUnikbd/QTs0bCnAFjr48mjZczl7hZdtmKCnnpwOnbUg9NEWkD4ECRNOC29RIAduK67BAnOUmcZC45Exes4TOmwo4/qeTpplLMTlIUBSICu4UdKkp0AeDD+2ks7UCXPJq/0mThmTGD+1LmZqVbNMkhZrQklD6DGw37kdCndon9kma3Z4hvEn06AvW3eNJmuZ6U7Qh9fQ6tneNbDNah5wmZnS1fVIDmI6uGcaf5sucGNi+kpsMb07Tmlq1Kd+mxubA1a52tWMe9ahHHbPccUcdddRrvvvd795xPeq0UdAEZZ3A4ESKeqJzGIyYhekfkZ765i5RvQvUBqSKXYFppAMfjuO/g6h+JBynBkBBmrNXtRoKUmfW6RciWZHAOABzPQmEs2rNA1zfmSbX8FgFk/XRtKIGQ7MM10DoarpQmKQfhaSL8jJlOddSeOhjIyFT08PxCnAFgUJEbY714HgXravmuDT3eKzl+ex9fj7XTDZmGc6u8zlZP4WYWghNRJp00g9GgqCmwfooyDWB+Ixt7/RFSkGZx9muEhRXvs4sqLmYnv1M058h8xK9TIjmtexXkg+QydSAZEmNTK59oxZHE17mG9Gnh/0Ss9SwAM1Nmlc4FmJp23ifXkvSkGZVtZqGGUt0JVrpYAx8TvYL+xd1N30AaHLS2EpogrKOYDBlZqctWx8FzQUKGn0iJA4MkDpA6jQokVEoqkZPe7tlOmt01i3SrKTg1fHWWSFlmxhLoqJpIZ1VFZgOsGobFGres6QBOAhndIf1YVuSp1T5azoxzDpn5jlblgRBgBQ+CjoFK8RNIaUWQWFiG6ZfD1B4OetVS6AmROGfs98kcJzHtdRieX8So3SO1K+Gb+sGyZLUZgI9fU2yP6ipYZ+JzDxO05CL5ylkfV6SB65B+0owOS/DdRXW6SeSQtkcJvalJDz2gfQ90r8oz1P7pkZEoiFh8VmkeUftk2TK9yLJt89ecqP2kPMsz/dEbWJqSdL85D7JlnVV46aJMUluhvdnX+JaEs1MhtgalMZWQhOUdQaDIAO9A7RqZsMfHSS1jyuozffAOZoyOFfBqoBwdqd6OH003O+gqLo+NSXW0Vmewi3JkAOxM8o0TSHI1KIoCByYq4Nj3mvmV0lzhCr2VL1XR123p9kjox+SnKkZsF6aKxRUtmf1jakL0Fme2iPr5PUzT4zbJQFqGNJxNDUDmnuAayvlDN1rKlQVhgplr+U9gNQ4ZZvrFJuRI9ZRsursXgILqZP0CuuQGjj7SJJZtTWW53VtV7V42WfTSdbnZ99MrUaGafsMU8OWkV22oUTPlPfcn6HzLvtge7ldWJ+aDdbfQJNobvNdsx4gfaHs9/b5LNv/jcZWQBOUdYKCzllikgd9P+pg7CzYgUvfksyBopnCPA7p+KdqPcMmHWglCM6EVZMDB0OFvk631jWFmRoGoCBKgQMM/8zZsddRmKqK9xpqXoDRM5o8FOZeW58Cy/M6EgiFoVB4pyOys3nbXfOIZVaykXW3LE0CIn9LShXgEsTUIuioq4nBZ2D/Sa2FfcffIH0iDCt3v7N/y/J+NKtJ0Jy56yhs/fwGuaxCtm22jyTV56GZyv5qPzFMPrO2ZtumD0f2mfRZUsvg9TRBZqSO/dDnorYvfUBSw6gmyHcgyWBqJX2W+sek47L70iyZfSP9aCQ6+Y7mOkHZvo3GVkETlHVEOl3mAmPO4nX0U3Ay2OlTokkDksKy7c4EFdzOui3TgVvywzadIM1Em/4F+jN4fiaWMpRV51j9I3JGl+YiB2adJlNgcF/43+AkrNBVcFQtAPdqeV5LP5R0bFWlrxABnM99eu9pCuE6lIMZSOIoEdQMklEe1DW1SrRH5rOQDKqh0u+HcsmXYXtl9Iu+LZJE62kbZn9R1Z/EAEiAcsG5FOBpntDUkFqh3CfpTN8Rn6sRR0n8MuomCan+OElc1CgZeeM6NraFz9g6pLYgw5pT0NtndbZNR94ko/bn1NL5bH0GmnPIfnvRRRdtoyXkk342vlsSlTQBSlysR5JArqHmTK2PGhLLs/3Ultp2Pk/vp9HYKmiCsk5QeDng6nehj4ARAkC1sH4cqa24xjWugdf3NuG6ObtPlXb+T3V3ag0yckKCkGHLQCGSpCD9SNymILC86jzoTFyn1xSUIKOO0g/D+0gtUN2eg7jbMzy61sN61/uxDm7jWRAOTqbf9EWRJOljoknLduP5QND23nvvkVDmTN06Jdmw7rUNVfdnu6SvTW2DLCv9PGr7Z1vVbTljt+x8ltnfUrPitaeEaJqzPGZWPSxval/Ce84+OEuQ5/1P9RPzy7B2kOV5vGTNd6VGtGWfEJJmNTiSF8sF+k45WVFDkz4qtW+3D0pjK6EJyjrBAVLzS4YBa05QLa+TXuaLMPSVWb9p50UlJbnNgd1rpXBITAmNPCYFZ72vKaRQy/tXyGnPzzq7f6rsJD1VsFt2mshSmGZZVahnG6WgTVKmySW1XxI6TVFG13h9hA8h2My+1SBNtdfUc6hCKNuonluPrc8niYv9qV53iijMKm/qeVdi5HH1ueRzm4WqAanXnrpGNV3Nqmvefz0+3wm1SJKTjLxJksgzryarJK+Wp6lQDWlmkVXLl/vUdqpJTX+m+jwajc2MJijrBGdcGS7sgGTYKFBdnjO29PTPQb7Ooqd+i5z51u96jGUn0oEvMUvgpMD3mKy75eX+1AzUa03NfOv2qtqvhGue4KvneI10Lla9r7DJdZH0p1ADZdh0JV21jauQTC1H1RLNqvM8zHs+VXuzvZi61kpn+yu9n1n9ZSXXy37KRz8nHXE1B+WyAfxOH6jUNnleLsUgcfG5ppnM7Wr2cr8mWtDkpLHV0ARlHaGwS9NFphxPElD9KsyamgmwZgmEKZPPFHmpmgi1FHn8VPmJWWr4qZlpRdXI5LFT580iUPWeq8BR81Hrm8dMmSncruodaKpwNq5PhL4Nhrk6+85r533MQhKW2jZT/+fNqhcV2CsRfPOIwBThqc9p6pxF/StmHbeo9mfWOf53UuAzy6iuXKVYH50MDQa+r2g/0oxYn2e+x1WTl/1wai2sRmMroQnKOiJtzM6yM+TRwVr/jPRFAGxTuzIlmGYJ74pFhNqUqn2KCNRjstx5grgeO1XXqTpOlTmlbcl9VbOS59R7miIIHqeDY5qVQOZxYZ9Oz1ParimiUeuT155nksv9VcuyKBlYlBzUdpl3/Lz6VE3D1LVTi1TLnXU9sSjZynN8pum4mhMByYYEBqSTs9c034rk1DL1U/HedTYXTkYyVb5mwowumvfeNhqbEU1Q1hnOyOvaLc70NSNIRDQFmU5de/YUVqIen6eOX24QnCU0a1lrPZhK2BZR5y+6P8ubZT7wWeT9GCacQsXy/C/prJi63hRxSaGe5y5yf8thOTIzVY+s52pNKiup13ohtWWSzlwOgX0udun7mFFMhnD73/01MZuaFyO19C3LBQrTQT3XYWo0tiKaoKwTHLQMtdRZlo95RtIkkCuieo6q4Vk+CYsSjKo1mNo3D4sIp3kkarUD7loJ51rmlBDOffoU+NwMF3a/wspzc0G+KTPMvOeU9ZkiKDsCy2nUartvNnODkTbpBGt0WWo7nShklE9qgXKpCBeGrFmfJTmG8Sf59dv9TljAjuj7jcZGRxOUBTHl1yGqQMtjcmbkrDrhfwYvIndcv0aCkhlNZ4WYzsMiavF6n+mcOU/VvpLBchYBWMRckHVzW9r+rW+11896Hsv5LEwJ5Zq2XegjlD4p/k7NylSdlrvfet48LKfRArNMJ/W6ea1Zz2h7NFjz6rrIfazkuov6p9CHeOeMmjHEX8d2szmbMVnioqOs5UlezX2j1sTcNxIfQ5vtI44PSVAySd/UpGQ5+C7PMutl2fW8RfrorPNqmastb+rcJmhbC01QVoApATbLDyRnRElSHIg01WRq7jojNweKs3WQDrZZl7V6cRcxA62Fynm1Zaz0+rP8Jqb+52/316RaPBOSluk0mQntgOsJuUTBjhhQV1vmoiQpsSubFxY1YwnfzySckpGMtEnCILHhd643Zb+peXM031QNmVFivtsufZE5VzxGrV4Ni5+VLyX7c45heT9pPpUwZTtkYsZ05teMZVmg+txI4h3vbBeva5tI1ryubQhcu6yGijc2N5qgLAgGin/+539eWrfEyBtfKF/OzFDpTEnS4exLIZZr0mSWzFy51Vmcx2R+hR1BThycctCaddxqr51lzrrGrPPWSmBWTVQO9u7PnBc+s9SEpSNkap5qGWuJqZwji6IS656N/v9QwKaGMwUkyLBi31Edp3NiocCemsh4bGrX3M92/VkcC1yf6Pvf//7w4x//eMk3xggfr+lYUpPWZX9NjWOOQ44t1WdKomE5mr5yrHJRydQIqUXKVdK5no7BmXU4w6xzfSaz+7LuE8TkCle4wvjd2FpogrIMeIlYcfi73/3ucOGFFy6lrZbJm/pdwuFAZ/ImwAtIeneOM/07ZUo2TOCWoar6pUhU/JYMrSRUdaWmmDq72xGY8s2YdVzWa2q7mGe+qcjycjac7ZbkBNMOAiKzgXqORMU1jhzIU7uyUq3PcmaY7cEiKvep9t2VMEuDMO94hX36GfFsTctvnhu+zYuikPVDf3Axz9S85BpPNRsvv12JHM1JLntgBA/b6H9qH1wCQ8EO/G09KJfzJDqSKLUelKOWLxM5qq3gt4nogGW6HIQaXutnYjk1iDke5jpR2QZZlsSJtuV87vFyl7vcUnLK2m6NzY8mKAUpSHjRICXf+ta3xoGDj6YZXix/OxA4k9EckBkjnYGkGjhn5EbvmO/EBdtyUEvVaK1rRapcF7nfKuhnDQLLEYBZJKLWdTlhMWsGOlXGlE19HjGodZy6RmoqkozU+1KTpjDJVZjrjHY5+MymyFs9fzXPZyWkY5FjVvJMdxSm6lDJ+aL1UjMhWbE816zK989reHwm8gMZOpzl54rMkl+0BPo2GRmWz0qyYyRRmkDSNKQTLteoafkl0BwjKchVuL03rwXJgqTwn3HPVcZz4iKRUxsiIcv3JbUv1Nl70H/Hd0en4vTJY/kPsjHXBJWNrYMmKIEc2GDx55133nDuuecueefX0F9fJmcIzgIqy/flr2pd91GumWQdOBhEXOo9NTFZz0XuZTnUl35HJIZarVlmOQK2SNlJWFbSJlWT4jPPJF7OINNenllAwdTAOq8eNeNvY2VYVINWz5FkYMKVKKbjsxpSzQ+++5k9WAHv0gjAPuHzNL29RCJNwUlc0pRrOWo30CxIGqwn+6ZMKGlaskzrI7kAOgdnsjk1IJaVpMv3QnN2vh/WX+Kh2SonWanZsS1cCRotM5oTF01M/5fG1kITlP8PqQk5//zzR2JiRE2GArpyqoMKLyjmGlcPztBgVaPOsjiWMjnWMGPNOOnv4CrEaa92VpTq3EUE+DysRHDmOSs1V6ykTvW4WUSkakEWMVksYvJJjUnuU5VtODhCAqg5Aw7IPk+RWq9F0DPF1WOlWhPg8T5bfrtytO+ek5RcqTm1IGk68f0H9gP7COUCCYPfSW6dDGWUkGn2HX/Sb0R/FImC0X8el2Ob51in1O7av6m/9+l2NR+SpDQ/279zSQ5JRy6EaP3S8Zc66WfHeXvuuedo0vFZdoK6rY0tT1ByhgF5wNdEcpJ5C4AsP9dbMXOkK5umTTpnYfqYOBj4kqaNNrU0vpSpVvWYOsNfbo2ZRWzw9ZzaRjnwT5lxlitvOTJVrzHrmEXKn6rjlHljql3qbzVKDr6Z8lyNGUDwoPVKAinpnGr7qXtdqRlspVgN8ZlXp41ApBY1fc2D95jaAScf6TuRmhIFboYNV4dqyYITC8t3vOC3BNf+ouMpqGbG9BNJ/ybvWXMJcFKUfiyW4+THsGodvnOsyeUc0pSTbWw9HQdpL4md5M42ShKfzsQcB/lCawIxMVJHMrMSs2Rj82HLExTAy/W9731vuOCCC5a0JrwoDiQ6RvqSOHvhBXUVW+3HqngVQNp8UZny7Yq3moQ8jv/YovmvU552XsrmfFXDzmqSyCynHQCLkpTlytie82chB6LtqWcta3vqlfeqvd/ZpHV0lWmff6rbnXXOu27PDHc+ss8pNEFmk9W/CKT/RiZ5y8mC44IaGSclvvNGtnidNPOk1qXmUqFPaQKmTo4V/k8i4viTWW4lC5qNvS+Pzyy3kjLvT5IlQVOzlBmwqY9lZ0SUzsa0CTBJJR+ICQTF+/R5qLVMLUoTla2FLU1QGBgIHf72t789/OhHPxq3ZSy+swZVmhkGl/kM+K/9NDNPKqB8kdmn17yDVuY6cObl7AHBp8nHgStnOYsgZ+rbSy5SE1H3LVLGor4z6Ri8GqzErDSvXmnumVJ3+2zTv8D9nj9Vts9ye9pzEfSAvjgUxghKNQUIz4zmyQywak7TZJH91r5gHzZCh2MoN002qZHxeWkeAUmSsly1eTi0MrHSqdXzJMzp8Ms1GIM0VztR4lg1tCBJiATc+8qP9ZJ4ZQCAJqXUiFAG5lHqwDfROfkOer6EKE1oja2HLUFQ6kDNfwYLNCZE6fCCKzTYDlQ9OsDk7EIHSXMUOMswHDUdYiUXEhhfdGca1cEyU6jnS2pos+pZCdKi9+89rPScikV8PVZS3tRxixKZqXKnTClT292X5G1WWT4bnzmzVf0UMpGVg7nPtOatqfWeRV5WSijnEbLV+ADV87a3DmuFfI93lOpfogIkAJmnKAkpkGRkWLH+HqkN8bwMG05ne/1I1DDotOr5vPf0u3zvJTcSC800VcOqP4rtZ7mOMZIYykkfFImF/nS5blg1YepXx3GMofbvdBJ27OIdwQlWjbNt4yfHQtu1sTWxJQiKkDD89Kc/HU06P/jBD7aJsDGfiS96Lonusuu8QIYR+/Jarqp/kxdxDsQiHed42Qzz47rOepyt6YnPccyKkqyk8+ZyAmEtTQfzrrUSzcgigjcJ4aL18jvPXaROedwscpJaMTVamvz4rrPJVIXn7LWWP9Wmy9V51nFrLaRX0neqac5tO6JOO8oclu+Yv01L737ebQRvClLJDO+uJEAnWFMOaAb2/XfiwhhgWHP6iVgHCYt9z/+5AGFqbIz2U7Crtc0s1CD7kNph+rFjGuOVY5STrwxVTkJhX6ddjGZK0mHggASPe2C8u+xlLztqT1LrOGXeaq1JY8sQFF4kBD5aE8iJL7J2UYmFqlfgAJPZEX2pcjbjC6xaNr3n0c74QjsL4Tydynyh07dBM46zKZdn5//uu+8+bquzyalZ+lphe8xDq8H2zphsi7Wot0KIwZVoLfpLalZSo+VsWBOhM87lBPZK67jez2MWsg4boT6rhe2pFowPQhchKjGQLKRPhBMZoOkXuEKx2lP3ew3GBPuVJhf7R+ZTApKTdLxXG+HYIdTWqbmzTpqGTJefTr9GLqkxyZwvmftEczRwfJOUS8IkYqkB0XeGtsTXhNwmqeUBaUrVhy/f4cbWxaYnKBIHTDnkNYGk+II50GQSNV+IVLfy8hoKp/aDfQ5W+qD4Yhk+zDW8nuUZVscL64CoHRtYL2cjnpuRAFNq7lkz9JVoIuZheweKWWSqbltpSG4tr7bFPPNNHjt1nuXbh3yGOkFLRCSu+iz5DDPsfFa5ua3eV72/7SUB84jSWhGM5eq6WhPUWpDOqX6R//WlSK0qyPDbfD/5QDY4zpwdlqmJJ/uP+9SkVnKh6UXHeAkI+0xlkGVmm2gOoX9SH7UpQHJiriW1gdmv6yrNGSYtgZCUZd31KXH8zMg2ttEuaEww6WQEXPqmSExs0yQuja2NTUtQcraCxoTcJppdUk2vwHeGUF9+Z0naYRVE6fyWZCcHWR1r0z6cnvYSENW2VdWcGRmtQ/qo1Lqutp0WFRKzsJaznOWI1XICeyVtMs8k4WDts+E5qcZOFb/nO9hmMj8J6Lz7mVev/L0WbbyjB/wdPdtdafmziO+UtjG/9SXjGebCkJocFMSgOjtnFEyNoEkNh++177kaE6+jwy5Am0OEn2ONBMTlMtJ8WschjpFMcCz39ZOf/GSJbGW/lRipCWGixbW4tkEDmr41iUvArX9qcDDn4ATLJ4lHtr11SK3Jap93Y/NhUxIUHcfwMSFNvS+ymhJfaGe7hgT6gmconepUBgkHFJCe7ZKWdGpzBq16VqSK2G+9+pPMgCQ/oDqMzVODrkRAV+3GjhZk2zMDTpPJSus9S1MxS/vk75r/gb6igJLIeI4k1gF8EXPVWpKQlWBnXXe9sCjRq/t0kNfs63tnX9E5NUlPalSrg7QkF2QuHTW5/nbswRTCMUQYSgCMDJMA6COjv0heUzNVTRqp9pdtOnrXqEA1IJaRbZPmTuus+ZoxEm2J2mHu4TKXucw2PjDpjyVBk5hs1j7Y2D5sOoLCi4oTLAnXXP3TwcXkS25LVWSqYX1xeNEyn4UDCDCqI73xnY0kUVGtqvNcZoHMF9Q6SHYysZu2X51vFzGDLGIWqIPPlLDeEZgytyxyTp3tVlKyiMCdReZs09TAJGHNiAYdptWosF3fIlXlCqXUjM2qz1qZcFaKJE+bUZ1eTWvznoGTmnym6ctR/U2qs2sSZ/0xjK7J0HSFek5UgH4rEiMmVanl1cTrR5NTOtLb9/Qr8Tpu0xclxzKjDx1/HF/U6kgwMtGcx6fW2XeEMZOVh820XCcTIKNz5pl+G41dmqCkQNI/AK3JOeecMw4cMHpTNms/1bSSiYycbeQaE85SOMaF+1KNm6afzJ2COtSX35mGjmpuozw1KzmryZDVzIGgwHPgFN7DlKCeeuEdLD23Hl/bdC2fUw5UdcCq9vQp5HmptbC+2RZ1X15nkf91e9Vgqb43qiv9TjIXSpqDssxZWpUpojJrAK/3OwtVSM8ioVNmjylMEcIse6qus85fyXVnnZPnLkcE89janyopTU2oBDTJRoYR+5x99oaiq3V1v5ORNAkKfUbQmqiF09SSGav1czJCJutqBGBqfFKDI4l2nDNTdtUS5aJ9OXGy7o59mq44D40JviYs7lf9UFIrnWbuRmM57NIERfDCoC35zne+s7QkuQQgCYcsX+IhQaiROg4uuYqmJMaU5gwYDhK8pGpIcqDKXALpmJve+NQTO7caE+vrYCRRqauEeq08viJJyErVqDlgLyo4Zgn8eWVUoVaFaBKXHChTQEtAPWa5wa8SpqnrVaQ63AHemaCDOfWwXxh+OpWvphLrHPznCfZZ9zZPyGeZi2jIVqtJyXvY0aj3NLV9JWUIn3H6hqSAVZPpJMe8Nx6rSU+zh2YZIQmpeUg4j/MddxwXJCX2L4/Ldq55eLyOfcXtEhs1JtbZPpEaQDW7amwzzDhNXRIVHGANHc4ElqlZsf2SUDUay2GXJyi80ETnkA3Wl8yBBqgm9YVSiPAy+fIBSYMqfF5Oc5hUtaovtlE+vtAOHpIJysdRzAEr1f+mrk9HOuDg5UAhadGkBGo+lOVmjYsI4HnnVuQ1kwTV8mdpJOp5tax5dZ269/QNWk5I1rKrFiDLz/LqwK4gyuyizkozeiITZGUd6rOZMvXMuv+6fZ7Jb5YmaaqMWe20EqG/IzRwU7C+STJXSsCnNGX57vo8Rb7HmkrSXy0X7cvlLpywOCmS3NpPXAbDvqOmxTVwNKVUs01NsZ+kKscNtciGDnvfEijr73jjqs3WP8cm+zv7CBnWCdakltmfa8TTSidJjcaGJyizhA0vC9qSM888c0xT7+rAIBMZKVx0CpOwmK+ED2QlQ0Qzv4kq0HR+M2GXgkpv9pyBpBpX1auJinLW4oACtP+6fk/O3BwIc2CtgqkK6Tpwe+5y2owkDCn887gpgVBn0ZUsVAFcZ2VZRjVt5D3ndlEFbF7TfTXxU16/1tsyU+XvYoBsY1B2QJe8AnPWUJb+R7PaYNa9uUidfUTNHQLFcNYsA+QaMlNtp5nA8ozuoI7ci8R+6lnPQvYnyjaTKH4R3AsCzLTmtU7+rn4wy2mDDPU3vNcoG65F1ItjwFQ7LHJPU46hIPOKsM3xIzUpvp9p8gFqMdzHsXwwR0+FI+d7rsYX8IwgM1XwZ64T/U1Ss2i4Mr95NjnxSZ+SnMSlNrI6+TOG0daYc9Tq5H7Hjc4E29hebHiCUgcZB1fXz8HnA/DC+IJxnKpXB830RfEFdbDI9XCM0NAO60ufIXWZYyAjPFTN8q02p4arGrKaxESikjkYclaeM/XMbglSiLrNlNUSHgWsi3mlfVrMEvBJHJxZMsh5zxI0E5hV3xaPkyjWWRTbsbu7sFpGUzkQVlV53rvPIQd52982cNaozxACOZ9ZJVzVx0WnWLfnyq4+n1z8Tfjcsm41kiHviQ/+U1/+8pfHPs5/BBLl0A5Xv/rVh5vd7GZLQjjrXNs0nxv3f/rppw9nn3326EAuiTAU9M53vvNw1atedUm4gEpM67WS3BHGf+qpp47hq4bEso+y991332H//fffJlqjErJZ95D9id8Qky996UtjZJ4O8L7b+EDQNvvss882z9Fr1X5S65L36rN0gqFZRoGrYJf0pU9GkhTfGa/nu0sb8XwdayQylmvdIXeep4ZGcmL97NOmywfW1TbXFK0TrvVNR133q8VRqyKhVZNDnUgWyTukxsg+LUnOclpj0tgebHiCkuCFNuEag6F+HelMppZDwWLuE51e9Q/Qq12HLmcy6QkvgWGWpnozneaYGSqEgGTBASLNRhyLIM5U9s6OLC9NAq5crKc9YB8DmzkRLMcBkN+0zTe+8Y3xGK7nAMd9X/Oa1xyuc53rLNmoQZIg/zvg5OBC/c4666yx/REOHs+9XfGKVxxucIMbLKWvzoHJNvEeqk8G9//pT396yXcIIaQKmUFwv/32G/bcc8+lMiQ6lg3qDA/he9ppp419RIJivyDC4Ja3vOU2DovpkJx1dT9tmaQxE+uZndMU4emXwrn0HRP3URcHcFXpOZOlbAT9KaecMpadwop2p22YtUJWrJsCS7W+xNd+rXbnC1/4wuijBTJ5HO2OwE/ibjva331fFIL2SevNZIHyXXjO1b2ZQDjTzvtODWf6eCXxqnmB+KYtIShoHvJ+uSbPnHpkZEk6kUoW1HB5X3nPEC21TEkCgBOejMwy/b3PKImEhDbJCdvpk3wkC16b66qFkXh4rloKE0ma8dr6SKCsB/2E/ZkFVrJbo8o0VfqpxMr3QBLI+4O2Kn1fLCfHj9aaNNYCG56g+BIyACF8TVOvQNCZS8Hm4MlgpjA0D4ACxJdWQaJ6mhePF5sXWQJi6KEDQSZ647fH5HbLSk2NL7KDGGUa0pgLDwLKMTkSREV1MrPfk08+eRvzAfsc2Mk7QDswUOeg7KBD2x199NFLg36qX03fT1nck8JUrRBlMwNXQ+XaHRzP8gGEdTPwpqlA4mPqcImaMz7Kp1zMdDlbdtBUQ+ZsXwdC9jlYs92VWDW9UIfvf//7SwOxxBXQBueee+5YrtokiJx+SSDT1/McKV+znnVLTZszXcmZgo3j0IggvLmmWhEFEWXkOiYM/jptJ9FVmJNs8P3vf//Yt0FGdNg/rbspxQEEQZJtf7BPct/f/OY3h+OOO26JWOSSC5IINQUuWqmg47/vTC4oJ4GAFHHvOpa7qm8uqqjGSy0oH56NJMPZPc/WJGMSsXy+tPUJJ5ywTdIvn6O/fS6+E6lZpZ1qRlMJkM8s+2hqZpOMeA3vg2PowxAr35kk//zOCELDdekvhjH7Lll2+j7Z9ukLp4Ot46dkWKKj9sMxNgmQ987Y434mITyfnBClxljUvE+NxvZgQxKUVLvygvJiI6x4EVVXavf1RcmZEC9JJiKqsyhfQNWXORvOWZC2Y2fNqSbOUGVzHuQsQn8FB9gMOTTCI/MM5D076CqA+A0B0KylqQaYOp9jGQRdSj0XCnP9DeqrGj41OKpj9XVIVbHmMq9lnb1PzqEMBD91U4Bp9rD+5pNxdqmQcRDN/xkVwz1RtvdkO2m+sg8o5BHEqKCTmOUzdLFINAdqGbgGbeJADxzsuQ4zR7VlqWJP05z3kT4AkCD6LsSCa/icNNvYdibdUiDY17JN7Fv0q8zVkbPdFDLZRzVH2G45O/e5u2Ccwi3V9pJ4+3kmIUuNpc/OurlfE5vCMrORqjnh4ww/NYmpuYF0JfFNHyk1o04QrGNqUyRCThqcUKgJsm7p92W7+b7UiDHvP0m5Y4ELgdIn6QtpRkmtUZJz/XUyB4rfHpfvUJqsnHRA5HxPHX+qBst7yHBpy5BkQJK4hzThWpc0X2d/aM1JYy2xIQkKUEXM7NyF9XKBLP5LQjLxkTNUXhheTAf/FK7pxKpQVo3NYOJvX2I91EEOjhyH4GG/s0PgLMaBKp1ZXRPD+jlQ+8LrtKbAoA3QBqDil0w4u3ZQcYAAKfDTD8ZBSHWxdctMjxk2nZqmtEsD79/Zo+A32gjqgjBJH5g0j0CSctVUZ9s+d69bHShpN/1f1GR4vG2Q5ouMZLAMB2hJmDNGBZnPz/O8huX629mogtTB34XgIEE8MwST5EetnNe0PWkrt0le83k6+CMwfvjDH27z3HL9GK7pvUhKeQbMxCWOkk39eyiX/WpldOIG1Nm+VHO++B74HmmStF2onxmS1RzYFzVBZJJC+5dtn8tS5IKatBV9IEmyTqeaba2zY4bPC6JZiZF9I99TtSOmD3DCYrs4eZDASI7Uqnnv3IOLhXr/1tl32DW8HHPUoqqtApII3w9/58TIe/caSWDTzOt9WY4+X2lK0xSKdtP+kqTZe0iTpu9Xmo8aje3FhiModHAGIAZiyIlqZL3lNbn4IqhNyRfT2Y72YeBLkzMvBz9nsiDX2PA8Z3CahHzBdR5zZWMHCwfuNAk56DmYWJbkhAEtB2xT9dMOamN0zk3zi+paVboMKN6TA5aEzHplqKD1UBDahgoeiZJ+MWlzV4XN81Fo+K0tX6EsoZEEqtZGOOYiZgpdZ6CSMs10CuYUSHwUsBIVBJkzcdtLx0Hr5azae7c9gIJCoSXRlVRKJHwmEkM0M7QBZMFzFVapbvf4NKPYFhKW7LOco9lPE1nVtiXJ9RmrsXFmbZ+WDFHXiy66aButl/ftbN2+oACSCNqfIZz2X98jiQh9OLVw6SdmHxCpAUpfGLU8tG06f9rHvY90/sz3KCOtfH8su/qhpNbRe/Ud95r57btlv9W0xqRCspYaSp+T7cw2nmtOYNKR2uvY/1Nr5D1U0ijpsH+lhs/n7/jmuKqplHcVYrLHHnss9cH0i0ktSnWCbWLSWGvsdIKSrJsXhcESu7XOhcnyHWQMKVbF6kua6mO3p800EyL58jlYOJA4szVyJGfQzkJAmka4XoYP1yiParO1XI4zmZezRJM1Gang9XWKA/x3RuzgwbfJ5fw42ElCnMmj5ciVUh3Y9YtIB1LbTVKhcNY84szR8Efrx33oNJnCImeItpMExvaSbDkDdbvtpdbLttXk4WzOMu0HQE0B9+4xauaczafvSGrQUiVun8qkU9SBemKCw09HIaTA8Pmmg7Sao0yqZd009eS1JU5q59RK2Sc0Tamed+avdlETg22kySbvLc1rqeVR0KHBydTu3r99Q/JpfdRGormokWuSN4V4vqcKWyGBNq27bWBbai71WO9RE5eESqFKX/V916SlFiTfG8tLrVBqtHxnfEfYrg+R72JqJmzL6k9i/05fGUm3Wi/bRFLos3FClCQrzWtpCvL6tqcTGcrifSHhGuSE/pdmurxf6+m2RmNHYqcTFMHgjJ8F/gYZtaIgA+lLkbNWXx5nt5mPQcHl7EmHtyQ1INW0voDOuq0L+xhs3aZwcSBwgErnXbUvOZsDziodwDT5cP+QNGbgDFBZVwVCOipWU5IaDIWgsyIJg0JSAayjp8JCQcGA6yAKmAmnwyJw5grSaRL4PCR9pgc3esFB3QiMnKHpa5LCMc0zXtcZvoO2tnKdpq2HhEP1voO+Kvz0jQESBheAU+BJVOtCcgh/HLjpvwgm/YMUfhyPcOc4hY6Cw4HetkpzF/8VIpJytSmW4UxYoQYkbApny8j+qGCTqEgKvYbEG0gGc50W+5dtKenzvVSDI1FIc5GRPj4734fUaGSfTI2PfS3bSZ+s1Op4T2nCSQErQU9Sn0kaPSe1Rkno0sziOMCEQv8dtUFOijQ9+Syd8CThUsPiu6wZyrHBfum7YR/O60k+vBbtLFm3nDRNUp7ROZe//OWX+mM15SQhrZqTRmNHYacSFAc9zBjMPFVhpwNizogcyHPwVFBICHJWrTD2pU/VLapYhbaDE+XrqJdOYamlMdLFlz+dClMb4eDtwOjszHtzlqL/irkR1EQg0IwgcQByAHX2iJDO9NkMRLnfHCLOylOtLPlL+34OnM4+HUTTJJJOhFkmsDyfQWqy9CtQrZztnH4f3Lew3Z0R+tyNrNIfST8ECZwELAWbMOJLh2LvxxwRlEtEhwQktWMO4BJnk4bxnxkoDroKndQQcC01UTofpoOi/gjpE5QCSVOZflWawFLrkzNqn4XPSAKZAlCSIbFhvwtk2k/TcVTzaqbw97ln8kKFn+8G9abcJGESrtQy+K4qZH1+vrNAwiXh8X0zAshoMerDvUno0gyGlsDn6CQgkyjq6+TEI+/VfmCf1pScJsY6aUpzsd9JctKRV7Af4iD5SRNU9c9SG5ITsTTFJNlXWyixwexHhA7Pp9bT8asSk9RuNRo7EutKUHxxfWHQEqAxYHbuC+5xaSfWZ8MXiMEo1cUeV2cSznTThq7A0GkxncSAA60DmKGtDgASk3xZ3ab5xkEk/WHSXu09OZtUgJoa3zrYTs7csg30W1EwOVt0dqzQV7ik+jkFmfsRIraJgiRJoSG4aRpzYFUroJB1ZpzrE/ktOVHo6iSor4SaEAmjZCBnw876vVe1FgrkrJttnxoa/WgkfKk1Sz8dozByhpumRLVFlIMw8XlJ7Hz+gG3026w77ZYmKAW2GiVNOPYZnSKzDRSCki3vVQFkdIw5gNKhkd+SMgmn1/IZ++x8LvQDSaXmHTUukh/vF0g21CSoSZNUpObDZ+Z7lmQ5iZw+OL7f6QAK0gSZWkWOtx6SdM5Xc5apCiwnnaHtQ5pcuHd8TXyf7D++AxKG9D3yfU7zXKYXSO1I9g3NcmkSUuuV+XTyeaWpVlLimGPmXcebNFclOfS+6nvcaKwH1o2gpP8ELwo+FqjEU9WYRCEZuy+lcDauEHa2lB7unpt5ChQ0btOU4QBiuQ6Iqdp14NBs4kCtVkGBlMJJPwoHEJAzeoW1vhg6GeZ954xd3wqgUHDwz3Y2OkGBnxlqJWWaftIR0vZUG5X3lU69Pkedd90vFNLOqIGDuveipgNIRpyNKtQkYZaTjoDAOir40/aeWhfb1+iR1HQliapagyR5GarpcTpru72q4q2nES5pOsvkf6khrKYQvnU8dbt9Ru2c5M06ei3V+pqK0sfBzL2p9QA+zynfiEzwl/fpc1STlVpD/UYU2Dnz5x1KQqf/k+RE7Vk6z2oCTFOv5jgnJoYaSzbUBkpgrYNkwut4DSZOSVTS7OnYgRlWopX1sP2sq4RMcmG5kkp96uxrqelVm6SZ0Gfn2OS76FjmpMBJS/q58V+HdpPnOabl2Ot9pLNxE5KNgYsnQd9kDLvSla702Z1dl/XCuhEUB1bDL3GEVUikMHaQ8kVTAPsyOVgbhudLrd091dWqdxUEqqa9nn4g/nbgyvBCB3cHbGc/qsZd3VjhXQdABb4ZaX3hU8PiwJaCSpLhQJWDaDrspbZEgZbOfJaRKavdnhoUyZgCO6+jNss2sI0lIdZb4WVbGHmU5hkHv/SDSPW+M72c1VvfTDaWCaIUotmOzhz1M7AdMxpLEmM7KIT0n8iEbQ7w6bthPVCTp/kpZ8IZvjx1Dc+rIaIKKmf6blc7ou+D2i3L0/TlQpeSgxT6lp2OoLa12U2rqSWFp6bA1BJkpJXmNgVr9lWJjW2gD0hGmiT5luBLmuyf1s1+aHuzDUIoKaGcXHHY8iWASQIsV+2Mbeh7Tx0wwyapkGxI0iWIfvTL0nRre/kuAzU46eRKX9cUxfHpp2Uber30mfHbZy/Bo03oJ5aZTrBJRvI+GhsL17ve9Q6/+Ln8j+WP3DzYoQQlVY68RGaVlBg4YwY5O0th56DtC5N5GpydK0gkIwrdjIBwUPGaDir6gujcmmGVDpRpJnA2QhmEV7oisQJNgZJ+D0YfUa5+AwoR78uZmapd6+KAL8lKR9W0S1tu+hvk2jsK/Yym8J7SyVE4CFqvbMNMSW45qUFI/6BUD6dvhm3gs1VVrfrZ+7df6Mvg7FEkubRfWZbEKcPS1XZIUvhtin7rrFDPxRv17wG5eBvXM+rGcGz7UPqFSLx87sxiM6Q2yYF9KE0+Eto0N/mtmcx+BtQ82f4IVomy5ivJ12Uve9klgS2ZTS1QElvbLZ2vEabcjw6ghklrHpWgplnUPmi/VSgqVNWSeH8SFd+ZJKpqCyiLT5pPLCP7tPftM0zCaUg417Bf+D4ZVZcEPbUY1l+nbIlhZqL2vvVfysSGvscu6Gf9JZVmePZZ2W6aXy1Hk7haF87DNyqJm+9tmoTzOTQ2Hi5+jj/cb7/93rCz67Ge2CEEpQoQ1KHkNOHF0xSTQir9FoALADr7zJmSIb05UwYO8l7bAUHi4MDuAJLOuNbTgcP08r6s1FvtiwOtxzI4p403yZUaIe6PKCXqhCOlM9C05XNs+t0ovBwkFbQOoAqe1PSkmUpi5kzWgdxzJV9qhDJXiMQvzWTW0Zml2pAkGZI/1fwOlhzjfThr1USSBMZ+kJoXnzF1QvCpxk/nvxz8JTSm1PcalpWmKY7lo8M0z0hCqM8F32rLONbnyf04q06fCQlOElo1IDooKiD0QUnNlWRPwS7J8xnbv2yH9K+yb3I/tG86ppqXJtd18R3T1AB8BraxTpcSFE2QajzUbtrfUwAqWIHP1XvQ7GH9c7t91mdhX0jfCNt8Sqvn80oNle+Q9+UYZKh5RnHZ/yVBOQHKZ65JVpLpeOXYkOY4ib7vXWoBLUPNos/b+/U9tkyfWdaHMYryXd3ZSQemHD62hZM2SVxqTrxmo7FRsMM0KHR+U33jSJYptnMNGomCQkjnSf0DHIxTfeoL7cwpZ1LOjhwonAFWZ686u1Xr4gDtoMNxpth3NqagTedXkL4RXh+k6Se1CwoFtRM5O3MQ9eOx3HvOUr0/Z4SZvwM4c7Zezn69NzVICkMFrWU4oHqPquUdhBMSHAf8VGNnW6TJIYWFgi7b33bXnGEOG8vkmj4z7fzWvxI/B2i1USlgvUfLTo2S/alqSJL8pJ+E2rnaz6ynpNZ7t24+O2fV+lukr1SWbT+xD2cb+50aN77VFKSvTrYLyHBrZ+H2T9tJLaJaNiNrNKt6bz5rNQS2O5D0eJ/ZJyRVaSb1GWd+n0zWZx/0HU+fMImgWrbUVOV9pslRAmAfSN8ahXz2kdRu2GaaodWo1PB+z5HsG0XoteozS/Os2hmIaL5HTiQwPbo2lffkMbX/ZN9vNDYK1pygKJjJC8HH2SQDmMKS/wzSClYFmoN2Xedmyjkz7cfO5tPZNWegvuw527eeEicHLbbXQUJbuyrs9A1xkHLQtvx0/vW/BMkBU6c5tR62jYOq5abDnAIyHV8zFNmZvwO+2hIHOk0oagMkAj6jJDgKRslfmgx8hppRFLAO+vosZO4OhY6zcEkqZanV8P591s6oHdxTO2Gbq51JNX1qFjLCRRNGCjWvnWp/NQfpo2NfVaCn7V4ylc/L+7W+3p9aPNvWuitY0m9F0ptmMNtfDZ7vSPXP0qSX70H6XllPy0ozqKa87FOSMvtdOhlXp1rNfZKnTLhnGZqZPC6z2NJHJV1pmvP5+ay8vu9H+u+olfV+JdVeSwKS44jPJScjqcVSq5a+G95rOrtKalPbm6Qt1x6yn2lqktg6GUmfrnRoz/fBfqGZi5wmvBfWI02cSbLSFJ3a6kZjI2BNCIqaDz6QECJ0CB/OF2G82P9nY3Um7GCZoa9+HIDSgc8X2nIVBtqsFdrmGbFuOcg6mFCGTqvpVGbIaiUkDn5pllEgOUvmfPNIpEOig4crumY0gYO9sE0Ubql9SdV2CtOc3bnfQZLtZhEFlOF9O2MzGil9KxzkjfRxwHRwdtDUjOC+DH/NAVQB5jNJZ+XMU0EZOkrnLNH7TbW5ZdPnkoD6zBR4wmeWM3yfW6b8zpm5Ql5hlyanJNBJQtJ/RlKi8KeuCmeJD8cZqq3K33uQaNhHFJYSNvufav9sT8mGbWa/qr4TXiuXk1Bbox+MREIib3tLgJ1w+G5YZ80jqSUzR5Af78130+edjtS+G7at77TXT78xkO+P9dRk5bteHZg1DZkxV+Koj48aN/slZhXJlfftBEr/mkxjYLs6kbKO9lUJs2VpAszInNRwSt491+icDAZIzWQ1pzUaGx1r1kt5SVjYjggdbPk6gTmjAq5ToWOsg5+CWoHCi1adVIGDqIQnBxtfwpwleE6aXFI1r4bAiAJgWTmoAn6rBpYIOAvTll4XH0vthYOXwkShl2TAmav5GkCaW1JV7UAtwUnS4aAk4bAuaiQUCDlw2o7AgVshl9Ec1tW6KQTVhPgs1ZRoLsjrZRkpQI10SO2E9fe+0nwnbIMUTprQMqsrkPyoek/Tg3UUEhI1etU8AezLqSJPc1maMPUTUPhnO1g/645w05yVZEoBpY8GUGAqhKuZI/2S+Ji0L8k35+u4nqYZ30v7q0TFdzUJk+Qs30frpy9PkiQ1GJK/NF9klJRt43FqR+wXhlBLiNJU6bFpzrI+6TuW5CF9TnKCk31XX7B0HNcPzPHB95ltGVXFNh1h1Wz5vnovqd3zXa9aHY8zqSPjpualNMmm5tZ6NRq7AraboPCiuA6JIXh63QNnyym4kiTw4QVju0vJO2uRFDgY10Ff4aJgzmiNJDHOfnzZgapcX1qFnoNtznKc9QG2SURUOQMFnjMmrwOciap9yYHS6BAHHgcrz3HwTK1JCg8dQa2b6m+JhyrsnGn7fJydgdQ4OABKqtK3xzqklsaZaUYJAdvSNpHEpAOkqu3UDKX2J817DtQ+X32DbI8Udj5zfyvsvCfbxPvKhGNJgNToaEqTuGnekFgl4bDN8x1JP4dsS/ur95UZfNNJVa2NmkCFZ/psWV/LzhBayYoOvkSgAdvBJH5pWkrH0zRfSdRSk5X+WNUnx/6YxEwNk+RZoS/JdPxIk6P9PM2P5nOxz6RZKbUb9mHLV5OmltOxqGoqrIPkTc2vk6XUUvmtg7ZjQ74r2V9Sk5iTojQhulBqTjpyDR3ChnG81ycttVj2vfretBmnsatgxQQl1YW8LITe8UFrokqa3/oGAAcijjehkkmPcqE4Z0P+TjV+OrSm85thhwpI1avAAdmZB8dq42eAVtikYLScnD1ShpEdkhX9VsggqtOeAjVnL8Bl5x18HJD9ztkms6CMCknflSQ2nqsaWLu9znp8G66rFsdnptADaU6xHSlTtXYmlrJd0zch65hqY8kA2w2PdMae5jbvMxNmjR0zynLW7Sw7fUwkChJUy7Zc66rw8ZnqD5X9yvIzksW2NFW9/UvBrhB25uo10VJUh9HsA/br6jdl+3gN+wbbzOeRYcUKRuvvc0yzDn3K1X6tswTC55Ph3PaP9GvK5+v96uyraUjBZ9unedMFA9UaJun3vfO+FajW12fmfaaTsu+ufct6pi+bwj99tvK9k3xI2tNJWFKh35uaptScSsx935wMSSbSR0Stje+vhIhjHEsykaJjQb7Dmo8ID8cJ1r6X/Udiko7ITUwauxoWJijpQMULgjmH0GESr6U6XpWnM1oFhi+5AwwvoanEHUxTPayJgJdQrUoVWl7TgS5NDTocOog783NgV+hqV1bgMSNRBeugqxbDe8lB02s5i3Vmls6VDqS2Y4Yxs93f3leqob3H1M6ohdBUYVSNg1KqcK1jzqhS6CksfA4ZKZHkLm39acPPyAzbIs169oU0l9mmPq8UxAoI28CyJEqpvk8/IdtQIWKfyOsqwNO3wetqDtI/yhlwmmGAAhZIzDSDWTfNObaZ74f3lMJSjYvPVHNMasz0BZJApnZSkmP/zBwsGdKc/SF9m9Q6ZOSUfkTptEp5GeFWzUu2RZpEsv8mSfRds03ynUjC57tqn61mDoV2jlH5XBXM1o9r2F5qq9SAZLST77nvYvqu2I8cAyQqkiS1RCDNY5IwSZZ1Sj8Uy/fdlJBYJnWhH0hOIJ7Vx8T29jrpA9ho7GpYkQZFHwb8TDDppE+HNuBk72k/126dRMdZloOCM7GcZfpiSmyc0TigJ2FQSKnGVWg66DkwOCCnmjdt4A72Rn9IDDRJWCcHvwxxTpLl4OF9WJ/091CzlD4lOqSmz0adGaWaXaJhmzpgauaQzEiaEJ6aQxQSwPZQ0PrMQTo0OpBrfkuVeKqqk3xyfPr6OOgrXBVwCkH3CdtH7Zx9x3v2fxIfBWw169g2tpXkUuFn2ytQ00RmPX02qts1L+qLoHYhhYb/JZBeQ8IhkpxIFH33FGaS+NQCpWbG9paM+P7ks0mHYN+DNLGlgM62pv9U043lW5a+FJK3mvMmzZXpi6KGzzpYX8tUoEsGKmFK53Gfm30ytUQS+RwjMuol3ye1jI4/trP3b8SW7eX4lv4gSVbV0KQDse+X2sbUsmT5TKAgJ7X+XlONVpLDRmNXxYoICoMueU0QEq446wyel8K1TnSO5QUxmoaXTuc8BgPUmb7weqA7OCmkGWBNopUvt2pQgP3VmbFkIRNSpaB2QNakwHlGseRMDbWpg6ECO00H2uyd5VE2miThTA94LwpRBaVESrJhPR1MbUMFpIOdmgG89b2WJhoHWgWzA1gKRc+1LVMrBjLZXPqh2O7CWapaFolbamsURGkKSS2KRNJrmDcihU5GbgAGaIWw5CgjSqqJQNLgcdmmnmNbW/dUzXsPChIJQ+63z6YGKdcpShPa+NKFs7Ok1P7sbD79ldRASthy1mz7ud+Pz8X66U/CO2wbJ4FL0pzOrn7bNgpnBWdq4dTWpVO1pMhVwK1/ajAVzr5vvp/ZP3KSkZMG65WmkjQjAc9JrZUCPE2b6Rck0XVykX50SWJmmTglH9XBWbKRY0MSmDT1ef3Uoqrtrf3S6ydxaTR2dayIoKixcCbiiwG5AAgPQyZ9kX2RcjblwKNQzqiRTNik7T81Fs44HbxT85JqagdDy5M0OODy28XNUqPjPo9NzVA6oUm8FIQOOtW3xOvYFsCBzsHStgAKHxdSy4FK0qZg0/HT+6/aD+ubA7e/UzNjndIxNP0jcjC2nZz1K6hT4OX9K1TcZxukGr5qWjzOvuIztn0d2DVXSBLTzJQCKjVz2S76E0CCNQtxH5DnJAF1ZgzSLJU+OekjkAnF1NwpPNIfQ+1clmG7JVIDZ/1sn9TgqR1R0yUZTxONpDe1jknsqj9GapIkEvleSKok4EnA8nmktk/tU2pp0hcpNSDZP/X/Sm1lmgXTwTrbLvu2Y5LvYDr5pok2BX8S7NTg5bhiH81rpXk287JI+tOx1Xct6yeBqmZc2ySjAZuYNDYTVkRQUnAlU09hm7MA7eE5yKRtGTgIqKLNwSOFbWoXPM7BFOjImjN1Zy9VDeoAqRpVDYfXqCvcAsqpYbvO9qrtOAfKJAdpvvLe89xsV6Da3X3Wr9r308ky28mBN7U33ov3ngRBwe+gbxuBSixt27zHvH//50zSts5nlAN7qrXzGadw93jrkrP49IWxDgq7FAI5S/WTbavGo56n4PXaPstKFnwuEvl8F/KYqdmy956aipztZxLDDJHN2Xb2e/tZCuYkX6lFyL5kBJkCMM0e2Y+8Pz81JNvyMorEZ1u1EOmnkto/iVbVunh8Oo/mmJQajez/9f3yOtneeX3Lzv7pPdqGtl9G3OWkJrWnamiqKS0JV05wbL+qQUvNSWpIG43NgoUJSg6kOQCmkE2bqCpqZ4p1puIAlrOtnD1oO08bbPqZWJeMvvBFztTQOVClo2oO2A6yIGeRDgQpTDMEOWdXkhXg4D6lok6SVAecHLz1ZUithE53OhfbXqrW1UiBFFoKmvSlyOeRJEZYH/cpfJwFKsSNaNKk4Sw6+0G2Qz5n66HZJIlrFeQKFwfmJEK1T9oG9q1qDvF8hUpG73h8EpEU8P5P7VIKmHRsTWJmeyig8jjrmsQqtRP2Y69t3fitY6+CXcHpe5MkMM0klZDaf9KPKElcDQk39Nq2kST4DK2/z9LyU6tkG1Ztnvu9T/tmailFthfHonn0f33eajJqP68mG/9nf7Jd00Q7pRXMa1tf3xffe69jGgDf/+zHORnLccfxxrZKzWyjsdmwIg2Kgii1KCnkQbJ+hZsvd9pgU2OSg4QDjQNDDtLOpnOWLEmpM2WFQtpjcwaTtt2cxatOzYEmZydZpiTFwR/kTNxzHVBSaFnfnDUpANKskeYBrmlIqG2bWoWcsblfIWAdHCAzKiEzh9pWtT6VrHjdzFNRBavfkpZs4xSKCkmFkc/Ktq0ESkGcJqsU8LZnksJsR8vP+5CMKAhSYGRb5rESyGpSy/6c2hXraBuogUlBZP9JE0r2m4xsSiKioEoSkuYk2zZNP1nXdPi0v6QWhv2+f6lpSlJdTQzZH1NrAzJxnP3Nfma/z4lAakfqu5nXrgQvy8h+ap+omqUkhPlOpbnN66WZz/6QTuvWhd+ZeNH7TSKTExTHtNTUJOGrJKXR2KxYUZixSDOO4XnOenIfSILiIJSzkxTODozpXFjVqdbFQSDtzB6TTqoOUJSRiaNy9pYEpJqUFIw52zb6xZBUBzBt90l4tA97bWe+SdjSZJDmhZyd5zPwO53kqrYntVWekwM4qPusQ7ZzzqQ9x+tah9SMSFicdSbR9Dxn34DtrsnirDIFZRLRnA37HLLPpA9SChifb/ajFGp8Z4homiO8D8/JZ5Gmi9T41fb0GpnRVAFTCY3COEltmvAU4tYh/2fytrxuDe3NZ5nJ5/RxyncuyYXfaguTFKSJqSZqBBK51FLV/mffSo1VJVlVq5aauNQU5SQp29nyqjkxSUKel/0myVCaxCrBTLONGpnM62Jos88aZKRWItu1nWAbWw0r0qAYxZKZKX350rEM+CI7c3DQyMEn1akO4M5KnSHnDCztxTmbyOuBJAg64vHfSJA628yZS14rNSXeQ6ryM3omByQFp2aLbBe/kxylaQYoMJKEVVOFA2z+TgFe26jep4I0zQ3ZVg7CmQskyYlCLH0anM2nqj81XpZpErOcvdu+Js2q4bOpidBx2vaxX0mEQFXxp2ZHeD/ZJpLE2h9EzmQ9Ro2U59suqRVUiCexsx9kX/fYXK8pBXrV6tmn+W8dqsOkbZQarLym29N8mpMJ+3Jq9CTXSaKyjZPopLYwna2zT1qvqnkyjUASj3yHJETZRqn98n9q5myTJIKpDU0Nq88jyxS+L1n/RJJVywI65mf7WB+zDVte1fw0OWlsJazIB4WXAxsvAqLOwhUiU7Ny/2dZdVZWj89j62wrtQD12MRUHXK2NkvzUElQ1VxM3VfWb169pvaDvFbWOwVI1YLkNXNwrNfIe5pqp3n1q+dkOXn+1H3lQF/rMnX9qbas9a7Pfqp+U/VY7lqzjs3jps7xt+/EvGvNa4N5davl5v58F+fd1xSm3o98D5ary7w+P4VFjq/lG0U0q/1rH1npdabGq1nnTT2fef1lqo7LPZdFjmk0tgpWpEGRpEx5jK+nF/laXWtX9XzfVeu9Ftiodvd5BGmlAme5Mmb9Xum15p27kvtZi/tbrh7L1WU17b6S6yxy3mrqOK/sRmOro9fcbjQajUajseHQBKXRaDQajcaGw/8DkbFJRXNf2B8AAAAASUVORK5CYII="
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The width of the sheet was $p_b = 100$ mm, the attached bond length is also $L_b = 100$ mm.\n",
"The properties of the tested sheets are summarized in the table. The dimensions of the concrete block were $200 \\times 400 \\times 200$ mm."
]
},
{
"attachments": {
"fb43c5d7-b9f6-4d4d-8406-9d7610039506.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmwAAAEyCAYAAABH+Yw/AAAACXBIWXMAABlvAAAZbwEQE52hAACcD0lEQVR4nO2dB7gURbaAaxVdc1oTomJ2VzFjTqiroq4BMWEAxJxQMaCYJYhgzhET5owoKAbMrmsAcw4YMee0q++9/+x37qvbt7un08z0zD3/9813Yaanp7uquurUiR3+5/9whmEYhmEYRmnpUO8LMAzDMAzDMOIxgc0wDMMwDKPkmMBmGIZhGIZRckxgMwzDMAzDKDkmsBmGYRiGYZSczALbI4884p5//vnEx6+00kpuvfXWS/07V155pfv3v//t9tprr1TX1atXLzfvvPOm/r00/P77726aaaZxf/rTn3Kf65dffnEXX3xx6GczzjijW3LJJd2KK67o5pxzzty/ZVSXP/74w915553ujTfecJtssomM/Sh++uknd+mllyY677bbbusWWmghGXfnnXde5HGzzTabW3zxxV3Xrl3dTDPN1Oqzeo6zJ5980j399NNu++23dwsssEDh5zcMw2hmMgtst99+uzvrrLMSH3/IIYdkEtiGDh3qfvjhh8QCm17XOuusU1WB7YsvvpBF54orrnC77LJL7vP9+OOP0kZxsBCffPLJ7uCDD879e2Xj119/dR9++KGbffbZ3dxzzy3vbb755u6hhx5ygwcPdocffnidrzA5u+66q7v++utb/h8nsH3//fcV+13p0qWLCGz/+c9/En1nvvnmc2eccYbbeeedW96r5zi755573JAhQ0SQrLfAFjbeDMMwykxmgQ0B6u9//3ur926++WZ31VVXyQLhLxKw6KKLZv2pUnL++eeL5q9o5phjDjd69OhW73355ZfugQcekPdZbFm00bY0Ey+99JIs5NzfmWeeKe/RvmiE0Cg1Ct99950Ia4sssogIKGi6ksDmYtSoUbHHrLDCCq3+P/PMM7sbb7yx1Xto9z799FN39913i5avT58+bqmllpK29Wmv40wJG2+GYRhlJrPAtswyy8jLh0kQWCC22GKLfFdWQj7//HP38ssvu1tuucVddNFFVfmNGWaYIbTtevfu7ZZbbjl3xBFHiJaiWRdSHxbSb7/91nXu3Lnel5IYxgigTf7b3/6W+HuYLtM+M9NNN13kd9hQoem79tprRQscFNhsnBmGYTQWdQs6wHfnn//8p5gl8J1BA7fKKqvEfgczBv5p7777rlt++eXdX//6VzfttNOm+t0pU6a4Z599VjQR+Ook1YAAi/Brr72W6veKpG/fvrKQvvrqq3L9+M9hLsbMNc8888gx9913n2imttxyy5bvoaF6/fXX3QsvvOD+8pe/iKYmzFyMhgV/vLnmmkv658EHHxSTHSa9pZdeOtZXL0m7Rl3ruuuuKyZm4POpU6eKqQotFf/nerL+pvLee+/JhuLrr7+W866++upu+umnjzw+SJI2RLumAhtjlfuYZZZZRBNWD7beemsR2F555ZVU3wsbZ5XI0r48x//617/k+ef4KBeGtM9speO/+eab0PGGEJvnfgzDMKpJXQQ2zKYDBgxwX331Vav38dEZM2ZMqPn0rrvucrvttptoXPzjMcMiuFUCMxEaB0w+CgLIVlttJYENmIgqgaM3QgewEPLbtUQXToQH/JhYQE499VTRhCD4olUZN26caFNUYJs0aZLbaaedRNjwOeCAA9xpp53WapHq1q2bCBjHH3+8tJXfPyuvvLK79dZbZfHySdOuUdc6//zzu7Fjx8oxOODz4rtvvfWWHP/YY4+5tddeO9NvYlLt16+fu+GGG5xfhY37oA/XWmutiu2etA3x+eL3AVMlr+HDh7uBAwdW/I1qoKbkWWedNdX3wsZZFFna9+eff3bbbLONmGwVNIy4GSAsKmmf2aTHM4+EjTfMx0WMF8MwjGpQc4Ft8uTJbs899xTHZkxeaCoQgvCbuemmm+Qzf8IFdsQ77LCD22ijjcRkw0JyzTXXyILPBPr222/HRrWhLWKH/MEHH8j5mcDZWV922WWyaGy88cbuqaeeqqit4/eVZ555Jl9DZODqq6+Wv5jagosoGpGHH37Y7bjjjm799deX99ASrLnmmu63334TXx3u87PPPnMXXHCBLI4scJh3ffhOz549RZDae++9XYcOHWShYoHjXAhRqjHK2q7Ba0Xw5tzHHHOM22yzzWTh5Lz8VpC0v3nYYYeJT9mmm27q9ttvPxFIJ0yYIMIjYwotD6bFKNK0IedHo8Nx3Bf/RxNcL3ieAOEoDXHjLEiW9kUoW3DBBWVzhp8cf0888US37777ykYDDWbafk5z/JFHHhk63rLej2EYRi2oucCGIza7doQ1hC/lH//4h5gxmFSDsOvF34aJXXf/aDyIzmRyHTlypBs2bFjkb55++uliJjnllFPcUUcd1fI+AgM+OnfccYcIjEzc9QZT2r333tvqPTRdmCfxRQIWmiAIuZjrfPPPscceK22HZhBtkELbsWChMcMsrYsVIIBgorz//vtbFmvaib6ijRBSWPAga7uGXSsaFu4L0yvfjyLtbxI1jDCPwInwCQjemLtwzMdcGHTm90nThquttpoIGwhsaInj7iPIJ598Iu0exbnnnivCoA9j5fLLL2/1HmZAzLJsZtBM7rHHHm733Xdvc76s4yxIlvZFI4nA/uc//1n+z33hG4qAyYZuww03TN3PaY6nnaPGW97xYhiGUS1qLrBhsiBdAxOlD6YLNDfslMNgcvV9aTielB+YLphc4wQ2TLCYhYKpITjHcccdJ5M5C1wZBDZ8Zrp37x76GQscJkJ2+kEOOuigVgIQ5pzbbrvNdezYUTRlPiyYaLkQeDnGF9gAIcXXrNBOpNZA04aZTwW2rO0avNY0pP1NjTR9//33W/2mmsTiyNOGaUGDF6e1xZcwCKZFtElR4HOJIBPme5h1nAXJ0r4IviqsKQhBCGzcE6Tt56Ke8TzjxTAMo5rUXGDDBMILcPxlR43j8fjx40XrEgaTLj5UQdBikM8Jk2gUTMCYtfCTwqwRBE0DvPPOO1lup3BYdE444YRW73H/3CtCQVT+qqDp7eOPP5bFj0U7zISjAR5h9x3mp4MPD22ox+dp16xmwiy/yQaBvHz4OeKEj8mNHH1JBMY8bZgWImExt6UBLdEll1zS5n00ZQgoaMvQDqG1Vm2RknWcBcnSvmE+p77ZPG0/F/mM5xkvhmEY1aTmAhsatEGDBolWAn8T6NSpk1tjjTXk70cffdTmO0RwBXfkCslB+Q7nDWZ1B0xN+LzxF61BGGhL2FWXAbSM+NGkJRhJiWkTNCIzCIsbBNsbnx1eYbCIY7amrRG2s7ZrVNRnJbL0JUEBCCGYNDFf8gJSVzAOMW1GkbUNawVa0KikzWgxeaYw11JhIGhuzTrOgmRpX/xX40jbz0U+43nGi2EYRjWpucBGdOB1110nu9ajjz5adrA4IAOLStjiR9BBlEBGxCFCW9hnwGeYUlm8Hn/88WJvpkQEzV4Iv6BCRxAWN/84hQCQqLZG48Riy2d52jVrKa8sv4nmpn///vIiJQtaJyKO8d+ifBmaM4IswsjahmWBslgIbG+++Wasf1we8rRvFGn7uchnvBr3YxiGUQQ1FdjY4eJztthii7mJEye2iR6MWhiBGqFBn5sXX3xRIvbiFiM0cwsvvLA4NWMaCWrqcNAmHxg+dcHkoo0M2h+0KKSkoN399B2A1gWWWGKJNt/FhIbjtw+LPgKKmqbr0a5pf1Mz/nOPRG1i5uK1//77SyQk/kxoUKIW4DxtWAY0clpzjhVN3vaNIm0/FzUWq3U/hmEYRVBTgQ2zBY7cmNyCwhpOvZrGgWOCWhjC/vElUs0PEzNO37DPPvvE/i55l3CaJ4KM8/ig5SPSDp+fIgU2FngWECDxbJLko0WDuQwfJxzP/Yg/HM5pC64pzMRDG5H3TBc+ono10MA3wVWjXSuV+0rzm1w3Tvks1ET5+X5cas6sZJ7N2oZlgk1NNSiifaNIO7ayjkV/vFXzfgzDMPJSU4ENbQUOzWhw8LHBHIr5jd0vqQSYFNnlEpZ/4IEHtgQn8BctB0KEpgLBrEpUHRMwpoo4EDY4/0knnSQTMZo6JmMmcHI0oU0qupQWUWa6OGBmrEe2e5zKieok6pN0BNR+RdtAolCEYxanYIoCTD74qdHWLILAOdAmoRlF26AU2a6qvVINR7BObZbfxNRO6g2unXxb1LdF4MfUhY8S36skbGVpw7JAihFIW+kgKUW0bxRpx1ba48PGm+YDrMb9GIZh5KXmPmyYFkgXwATIC4jAYuLEhMNEOWLECBHsVGBjx0uiUjKQUyEB0GyQP4nEmJW0V2j0EEL4vu9IzASMTx153IJRdM0AQQLPPfecCF4IuLwAzRnaCJyogxDggQBN7iryiSn4Q5HHyjcLFtmumJ7oe1IvHHrooS0VA4Kk/U1M8AhVJD8lt5zCIn3xxReLL2UcWdqwLJAXDmhT8h+STqdo8rZvFGn7Oe3xYeMNga1a92MYhpGXQqUUSvBUKsOz5JJLysTKrpUAAyZOFcyA9zA3zT333PJ/fKcUAgxIAYLpAl+qsJI7JOTlFYQ6hZhdKW1F+hAmb347rkJCHCzWvKJAyPRL21QCbUia45NeB1oxHLHxY0LzgEmHDPZx2dox4ZJiAg0Skbyk4VBtTZA07Rp3rZjIESrUfEdkpuZ/y/Ob+DYhgHIfpH7AlM57LMBJzdRp2pDNR5p+xGE+bb8jLCb5Dm0SPC7rOIsiTfvG9X/Y3JH2mU1zfNh4S3s/hmEYtaQuaiUmvmWWWUZeQZhIVVgLQhoDv6ZkFtAgVStirszQptQKTQOLVFKH+qLaNaoAeN7f9PP/ZSVLG7YXimjfKNKOrTTHR423at6PYRhGFprPDmgYhmEYhtFkmMBmGIZhGIZRckxgM1og0OC7776r92UYhmEYhhHABDajBVIiGIZhGIZRPkxgMwzDMAzDKDkmsBmGYRiGYZQcE9gMwzAMwzBKjglshmEYhmEYJccENsMwDMMwjJJjApthGIZhGEbJMYHNMAzDMAyj5JjAZhiGYRiGUXJMYDMMwzAMwyg5JrAZhmEYhmGUHBPYDMMwDMMwSo4JbIZhGIZhGCVHBLaPPvrI3XDDDfW+FuP/mHXWWd0ff/zhfvzxx3pfilFF6Of//Oc/7ueff673pTQVM800k5t22mnd999/X+9LaSpmmWUWmZd++umnel9K0zDzzDO733//3f3yyy/1vpSGgrnzT3/6k/vuu+/qfSk1YY011nBrr722/FsEtm+//dY9/vjjdb0o478stNBC7t///rf79NNP630pRhVZcMEFZaL+4osv6n0pTcW8887rpp9+evfhhx/W+1KaCsbrr7/+6j7//PN6X0rT0LFjR5kDvv7663pfSkPBWJxmmmnclClT6n0pNWGBBRZoLbAts8wy7rbbbqvrRRmGYRiGYRjhmA+bYRiGYRhGyTGBzTAMwzAMo+SYwGYYhmEYhlFycgtsDz74oPuf//mfisdNN910br311ov8/Omnn5bIrvXXX9916GByZBreeust9/7776f6TteuXd3ss89epSsyDEP55JNP3OTJk918883nVlpppXpfTsOTdM2BFVdc0f3lL3+p8hUZRm3ILRltuummkp6gEnPPPXdLhNFxxx3n7r//fvf3v//dDR48WN474IAD3DPPPOO++eYbEyRScvnll7vhw4en+s5jjz3WEnliGEZ1uP76693uu+8uEZbdunVzDz30UL0vqeFJuubA+PHj5XjDaAYKU2Xts88+bsYZZ4z8nJwzChqhp556yi2yyCJF/Xy7BsHrkEMOafUe6SJGjx4tean23nvvNt8hVNgwjOoycOBAEdaOPfZYt9lmm9X7cpqKSmsOdO7cuUZX09igBV555ZXdWmut5W699dZ6X44RQWEC29ChQxOrnv/xj39ILhXU1UZ+aE9ePi+//LIIbLPNNps788wz63RlhtF++e2339wHH3zgllhiiRZLglEcadYcIx6SIpP786uvvqr3pRgx1MVZbJdddpFXJfBTIKNxGuK+k+V8Rjxp29T6wGgvqJ8VVQIMwzDyUheBbezYseJ3te+++7bxL8A34dRTT3UXX3yxONIvuuiibvXVV3ennHKKW3jhhUPPM2TIEPkeviI497766qtuqaWWkmP++c9/yvmeffZZUftyvp133llMiO3dV+7uu+92l112mdt6661d375923xOMuVrrrnGbbPNNq5Pnz5u0KBBkkH+qquucmeffba74IIL3DvvvOMWW2wxUaXTR2TvDmJ90DhQ7uX8888XXyvM6vPMM4/beOON5Vk1wSM5F110kbvnnnvk3++++67r0aOH69Kli2najNKB//PEiRPl3y+99JKM1TXXXNMdeeSR9b2wGoFWceTIkeLXTalA1rOddtrJbbvttvW+tDbURWB7++233R133OG6d+/e5jP8ErChU6Jp1VVXFQHsuuuuE+dRBDQGUvA8O+64ozviiCNEmPC1NxdeeKE7+OCDRZijmgM+c88995w78cQT5TcmTJggkVvtlSWXXFLaj3YME9jOOOMMKVl2+OGHy/8fffRREYb32msvEZQJJCHa9IUXXhAh7r777nPjxo1zK6ywQss5rA8ah/fee08c49ko4XPKxIWwTb+ed9558lc3QkY8BFjxXAE+bPjtzjnnnHW+KsNoC5tonn1AYGGssqluD+C2wJz34osvyoYUn28UCzfffLPbYYcd3I033ljvS2xFYQIbQQRzzDFH6Gc4huLQmITbb7/dXXLJJSIUwA8//OB23XVXd+edd7oDDzxQIkmDJjUiTP/2t7+5m266yS2//PKy2DBZIijgw4WmSFOKULetd+/eIvzxeXsues/ii3CFUPz666+7pZdeuuUzHuAnnnjCLb744q2iSb/88ksR1tAU4EgNFIRGA3fLLbdIm+puzfqgsdhjjz1EWGN3eemll8oExoR20kknuWHDhokm9vnnn3czzDCDHI/J7+GHHxYtqaWraA2R8GgoaKu//vWv0m5psLatTNyaA9NOO60UzlasTcPBWvLRRx+JXzlKkmAkczO329VXXy3CGto0IrqpQ0yKMea7rBrGarZXYQJb0OndhwkLzUwSkGpVWAMWDaRcdvtoZtjlB82of/7znyVNiC4kwCJDEXW0RH7+N3a51157rQgrnJfB2p41PLQ3AhvaLkyeClpNBh6CVRA0oyqsAbsS2vTJJ5+UgYqgh4nU+qBxQGAnvxXRw1dccUXLs8QEhnP3K6+8ItpYJjiNOj7++OPFfHrMMcc03URebVgcCLpioxmGtW1l4tYcQJjzC6tbm2ajmdsNYQ3YpDLXwWqrrSZzXVaq2V6FCWxoWKJCrNMsxvihBUEgY/ePVgfzW1BgwyTqC2uA0EAC3u22267N+dD4bLjhhjJpYvLZaqutEl9fs7H99tvLwEI75gtsCFSAdjNIWJoQBjt9hz8hWlAENuuDxgFzN2y55ZZtniXg+WYSQ9Ot/U//MmYOO+ywml5rM8AmBotBlMBmbVuZuDUHgp9Zm2ajmdtt2WWXlb9YjVBEzDrrrLnPWc32KkxgO/300wsJscYEFwZaOlC/EB9UuT5odTDpYTolYCEM7PaAY3V7Bj82dgGYbGhb2n/SpEmiUVl33XVFsxnEN52GvU8ggvVBY4FjPDAewtDn780335S/d911l/iMIpyjmUP4NpKBe8Bnn30mpieeL54zH2vbZKRZc6xNs9Hs7davXz95DnHL6dSpk8xzJ5xwgttiiy3k819++UX8s7E06QaAORCrVJgiotrtVboaUGG7e/998sUECUav/fjjj+73338XXzZyIIWh788777x5LrcpwCyKwIZZFLu9atfCzKEQtQvR96lWYX3QWOArCpWePxzoYcqUKeK7OHXqVPfxxx/X5iKbBDYyLARsWMh9FcTatnisTbPR7O3GvencR2lMNq76f2AdI0KeTAkqsOHjdtppp4UKbNVur9IJbDg9I+kGUc1alAbAB9+FueaaSxym2c1a3q94MIseffTRYhYlIhQzJQs074fBoCSKNwiaNUBrYH3QWCBcQ1TiTDRCoMI1gT6MFyatMLO5Ec2AAQPkGSO1TdgzZm1bPNam2Wj2duvfv78Ev+FmdeWVV7r5558/1/mq3V6lE9jwkcH/KQhhtkAuoyTg0E4UEarLsIoKZP9HAiaaC3+q9gxm0FVWWcX961//kkFLxBBOmFE50u69997QOqTqqKmmUeuDxoPAkTA0csxPq2MYhtHIEKwI5AnNK6zVgtIJbOTt6tWrV6sF/pxzzhFhgjxeSQv54tCLsEDaCHKDEcmoEGnKLhffLRLmGf81i5J/5tBDD5X/R5lD4dxzzxWBjv5QRo0a5R555BGJMtQAAuuDxgNhnNx7vkCORhUTwDTTTOP23HPPOl6dYRjVhDxs7QksBigoMIX6+UPRuuGyEJY8N8wtq1aUSmDDgRRTHCkgMBeQZJXoNTKGTzfddC2LRhL4PtnGESLIzUYkKRI0DvX4aBF5SjoJ479gmqFQNZnuierdZJNNIo/Flo+mBZUv1SfQyqAZBaodqK3f+qDxIJULm6L999/fLbfccjKRkTSXwBAin+hHwygD66yzjkShx0GVDiJyjXjwNQZ8mYluxOLC/N3sEHRw0EEHSYYDUnygcECZgEWPsaXBViR+VzRAqx6USmDDaZ1ySWhvKE2l4C9FXjAe0KTgM4W6Eyd6SiiRCE9BksYcF4zOas+Q2ZqqBUS3UOeVpJNRYB7DVk+7KgjbhEaTXFWxPmg8yCFEWLqv9cQfkc1SM4b11xM2RwobGDalaLqNZLz22msVj9EF14iHZ3y//fYTCxcCLj5Y7UFgYx3DP568acx9ChYG5jwsQAhuJOXH+oS1gXUO/2ylls9uboGN9A1pwUTGyweTp0KuNSR9VJLkKYoqkxF2Hh/V4IwYMcK9/PLLUi6GyESc4pvdCZ78Mlp8OikqpMWZQ4GSVAhiOKLjn4ZAjd9aWJu25z5oREiRww4T30ImMnbe+I1qUkkjOYz9qGeQtAG4BFAGiOcDTTTR7iawVSbLmmNUhk01eTSJkmwEf64iYA1CcUCpRFJZYe7Ep9u/fwLy2KySRoZnmjKYCG1KLZ/dUmnYfJBsi8oSTCMnLY3VXmGwksAWk5dvy48D+z8mhyRYHzQWmAZ4xREsYWMkhwWCiZ/nAqgQgoZDsbYtHmvTyqA58rVH0B7ajQC7qICqk08+WVxEvv32WwmkQ8jDP1up5bNbWoHNqA3kg8LRVM1d5lRuGLVB/YZg+PDhFUstGYZRH9C4RWkda/nsmsDWzsGHjOhQTDfkuPPruBqGURvw86zkQG8YRvmo5bNrM0Q7Z6ONNhKfEEyhBAVEZboHEhrjf5Y0UtdoHHAypm8tz1p9MGHNMBqTWj67Nku0c1Dn8koC9daM5qRbt27yMgzDMMqJCWyGYRiGYRglxwQ2wzCqCil6SL+DryS5Fnv27Ck5jjTBsmEYhlEZE9gMo4EhFQvpN8iFVwSEqJPDj1x7RUAEMsmUiaKiTi353XbbbTepHUtVDPwnqYSxxhprtIqarDd+u5JvkCzogB9nkmSsEydOdL///rukANhwww1bfUbYf1h5G44lDx45CvP6xTRCuwb56aefpDQalVM+/fRTN+ecc0oaBfwqK6UEsjYtbg4omvbWbtW8XxPYDKNBoSIBQSNJMr4n4Z133nEbbLCB++CDDwo5Hzz33HOSAJvs6QS0sHASiTxmzBj5nAzh5DliQSaBZRkItivl8QjKAHJDck9xvPrqq9KOgJAQTPS6+eabSzqdKGiTvffeW9olmBMrKY3Qrj5k2D/mmGPc119/Hfpd6hNTfQMBLgxr02LmgGrQSO3G5oxk1iTsZ8MQBVURXnrpJXfbbbe1+aya92sCm2E0IL/99psIPvvss4/r3LlzIee8/fbb3WqrrSZapKJg4nvqqadaRR+/+eabrRZeNG3UD6YkGuXR6kmldsW8y/WTAicK6hAmYY899hATsfLrr7/KuR988EEplUOZOBaWrFHZjdCupBMi6SilCNGGUW+YusYI9l999ZWY0akEgYDPv9GKxI1Pa9NyUvZ2Y6PAOLzxxhtbjuNzNpozzTRTq+9TAYZAvauuuiryN6p1vyawGUYDctlll7nXX39dSoQVBQJbjx49Cjsf+JnTd911V1lwMYeOGzeu5Zi11lpL6gST+b/eWdXj2pUdNxM7k/qxxx4beQ7qDpI5/fvvv4/9rZNOOilU+KBM3/rrry9tdfXVV7u+ffumvg9ohHalHBLCGkLWnXfe2aKZVNCCUJybUl7cA5pOTKZRWJuWk7K3G0Xgx44dKwnkV199dfnskksuEQ35eeed1+r7gwYNcsstt5zUPI+iWvdrApthNBhoJc4991wpC9axY8eKxyap2YopgIVw1KhRmc6V5HfQnqy44oqi6bj00kvFBKb06dNHJk1q0yYtjVY0ldoV4YE6q3ECG+ZQauZSj/e6667LdB2rrrqqVBzhWtBOxgkXldq9zO1KqZ+jjjpK/n3OOee0EdYUglPYTCy88MLSHvgTsmCmob20adzxeZ7dIs5T1nZ744033B133CHl4k444QR5Dy0v94KpHm0atUIBDS0adOaBSm1Wjfs1gc0wGgwmC3wvjjvuuNDPmZQoVHzrrbeKCQ9tD47+gwcPbvETuuKKK1p9B+0G5ks1Vd5zzz0iVOGrgQ8aE9mkSZOkPAuaCvyJmPBOPfVU0SjhzzHPPPO4nXfeWfw31ASqjuCYoLbcckt5MXmhyWP3qUXl0ZwccMABsnD7hZVrSaV25Z7wpRo9erQIZQRnBFFzKIWgswpsgEkQ3nvvvVbvo7Wjja699lr3/vvvi3kHjdLf//53EX5IfuxT5nYlCIVC4126dBEBNw7GMNqzxx9/XHyM0gps0B7aFIp6dos6j1LWdmOTBWzIfPg/2l8EOg16oaoBwh5joxLVuF8T2AyjwWA3CEwcQf7zn//IRIEAxoSJ/8QXX3whAhw+QGjS8A0KEjSHvvvuu/I7mAHx1SBSb5ttthFTAQsbk9zSSy8t3yPhLhMYEX5M4hQ0RzgE/I/QSKHVUIhA/fHHHyUqUAU2TGJEVeGrlGbHXyRx7aqgJURg455YlIIgsM0xxxyx50gCu3JYfPHFW94j6nTbbbeVPqC90BphsnnhhRdkQcDMTEDEfPPN1/KdMrfrhAkT5C/BAEl8yg455BB5ZaU9tCkU9ewWdR6lrO2m/qiPPfaYmDEVfB25Rh0vjAWivysFHSnVuF8T2AyjwWDCZBJhNxsErQXCGjvCu+++u6VgMe/hc0EkXbCI8XfffeceeOABN2TIkDbnQxPH7hkTAaCdQCPCpMWE/vTTT7doO5i4WfyInNLJmkmcXSn+IaT2QFAbOnSoTGQINj68h78HCyum01oT167KJptsItcdJrCxgKFlwNymgmgW0MzhZwX+woLjPNdIGTkWDo1iQyOEkH7XXXdJO+N471PWdtWFD81utWkvbeqT99kt+jxQxnZbZpllZExgEiWiG8GU+RDTKZpftLtYCtC2EkSQ5rqLvl8T2AyjgcA0gUkITU8QdnE6SSK4+YIZudCIekLjFQTTB8eG5briezpRwyKLLCK7UHbSTGC+aQoNHb4efloQPidJLudg143Axu+wQw+i0VTkgqv1ZB7Xrj4IYmgZaF/MQ/51+ubQJBCE4ZuNEBKIaNT243d4KWhHaXuSEPspB7imXr16iXDBPQQpa7t++eWX8jcq4pZgAzTGQcir5vs/+rT3NvXJ++wWfR4oa7uhNUc4w/yrcBxCm36OKZWNbxqKvl8T2AyjgZgyZYr8DWrJ4MMPP5TPEYjCfHyYkMIEtrjoUCKmgujCxu4xCNqnb775ptV7LIY4fLMb/8tf/hLpJK33VGQeuKTEtWsQBDIENrRsQYGNtkni3wJodMIg1QBmQjSTPuzueQVBa4r5JoqytisbDAjmqVOI5gvLrUabRwls7b1NfYp4dos8D5S13eadd143fvx4iR7VPGzq80hqGHze8EdDWFUYIwiBvBdl7iz6fk1gM4wGggzwgOAThPxAoBNNkEUXXbTNe0xG+GagSQgjmIPIJ00Wb47FjBKHVlfQe6wlce0aBIGMVCUIbORbAnbfmEOJCiNxZhJINREUXvF7Ie1JFAg5LCoEk/DCLIVgQUWJKMrarrzH52jAgo79gFlKhTpAWxasGhGkvbepT1HPblHngbK3Gz55vHxI60FEs24ScCHBlxKtG5sNTKYEZPBeUHAr+n5NYDOMBkIXkWAEFuiuNqpGZ9jkik8Hpkrf2bZe6D1hNq01ce0aBIEMjSRO6fjvkGwYHx9Iag4FBIs0SYop64V/ELnEgIWHfE+kGCHaUoXHIGVtVzTBmOMRdDfbbLM2n3NvPhxXifbepmWn0dqNOXXYsGFu4MCBLYIeUbBo4/BrJFIcM+mAAQNEWAsGxRR9vyawGUYDgeoewiI9VbOGaTSMMLU8UVOkqph22mkLvMps6D35EXm1Iq5dw8C/BYENLRsCG+ZQtG6VNEB5QHuHYIFQiHlm7bXXbum3W265JfJ7ZW3XTTfdVAQ2/ITwV6u0kKpQVSTN1qZlp9HaDYGdDbAKYmhwCeYiEvbwww+X9/r37y8pQAhCwv3D17IVfb8msBlGA6E+Eeqw7YNZicWGSYVca8FaeETE+RD5RMh5vXIiBdF7SuJHVjRx7RoGSV4xd6BZwz8P7Q9/k5pD04LzPdpQHLqJeAwK2GoOD6Os7Uo0LU7ebCQoAUQG+SgYz5rUtCiasU3LTiO1GxtfcqhhElWrBUmbgUAMH/7P/Mp3/GLyRd+vCWyG0UAglGHaDCv2jK/J7rvvLs7amHSYaHS3N3XqVElw6UMSUnKhJXWSrzZ6T/UI949r1zDI1dWzZ09JrHnooYfKe2nMoWkhTxkaKIQMfLl8szdmPTKyA58FKWu74ldGEAyCG07dtCmmJf768F3MT0X7PTVjm5adRmo3NhP4/fpVMTToAF9HP7qZtB24lgQFs6Lv1wQ2w2ggSDdAUWGi4VhogosbuYTIgUSNxldeeUXMTjjMkkaD3ENMOJqklOjQzTffvDS+MCTX5dpIwllrKrVrGAhoCGykN8C/Jaq0UhHQLvQlfdu9e3cRYNDmkVqEbPRqcsFESwknTDNKmduV8j3k9WLc4idE2TLy9TFO0aqh0SA7PXBvHFMUzdqmZaZR2g2NOcmCmSN9zSsmc/K2YT4nSpRofKwU5KojbVJQw170/TZOTxuGIZDkUTOw4z/lg8M1JlHyJjExaZoDFiTMd5SF0ig6/NdwqC0LaPzINB9MqFsr4to1DMrzsKijvcRxvdoL50UXXSQRapjxHnnkEXkPjQG5sI4++mgxyZIclhJOvnBR9nbF1EnqCO4BYYnNhoKGGL9ATKYkt8V/CO1GUTRrm5aVRmk3+p/gE/x7fdCi4dvI/MpmQyHJMvkmgxR9vyawGUaDQXJQFhMc3cMmHYIPKEOFbxA7RXwqSKmBzxo+FkTnEbXELnGLLbYI/Q0+4xXG9ddfL68wsuYboqgyedqi8mvVgqh2xfTpp5dQ2HnHmemi8ovFpYuIAw0p5ZzIE4V/1QILLCC7fdUAsMtn0fCjgcvcrj5sKHhxb2jV0K7hI7jKKqu0ivocNWpU6PetTf+fop7doueAsrebwtyItpzxGAY52hD4nnzySak9yyY4rLh7Ne7XBDbDaDBYZMjCjplz+PDhrVT2RCzh6EogAYKa7wCLdgIhAuGNBeiwww6rx+WHghYDs2JYEtNaEdeuZQJfnLC8ZRDMMdVo7Rp3b9Wkmdu0LDRKuyWZGzGvomGPoxr3awKbYTQgRxxxhCRuJAcQ5jgF8w4Rb/jcULNT/dVefvllmYSYaPbdd996XXYoXDMTKA7n9fani2rXRsTatXisTbPR3tqtWvdrApthNCCYbSizQ3QdtRFVMCMSlLp17B6vueYaUd9TL5HC5GjXOL4eIfVxnH766eILxkRab6LatRGxdi0ea9NstLd2q9b9msBmGA0KEw5h4yT+XHPNNeU9Jgl8gEhJQMAB/iT4AhGajgMtEXhlAiGS6yUVCdq/MhDWro2GtWvxWJtmo721WzXvVwQ2osp22mmnQk9sZAPnRRxo33jjjXpfilFFCAdHbY7Tal5wpI0DJ1p+h9qMfqRbmdhtt90KOc/iiy8u+eg0wWUeKrVrI1BUu+L3yDjCiTovjd6uRbUpNStp06jKJGlohDYtqt2YO/E9I6I4L9Vst6Lu98ADD2zJ9SgCGwngyCdk1B/yuBCRRp4Yo3lh50XUpvVzsZBag1QQURGaRjZsXioexipt+vvvv9f7UhoKzXXWXp5xkvcqIrCRI6Qs2c4NwzAMwzCM1pgPm2EYhmEYRskxgc0wDMMwDKPkFCqwkbCT2ltkV+ff5IJaaqmlJHR29tlnL/KnQnn66afd999/LwntGqm+WlE8+OCDoRnZg+ADQE01snundXrv2rVrq74kCnH8+PESJEH6iM6dO0sCyq233rqQPq/3mDIMwzCMMlCIVIMj6imnnCKJOn/99dc2n5NdmM8prltNKKNBOYhvvvmmXS7mFDJO4hRMmofPP/9csuGTrysNjz32mBTAxWGekhtnnXWWFMENMtdcc0mNQDLvZ6HIMXXIIYdINBYFnQ3DMAyjEcktsLFw9+7dW+qKzTrrrJIojgKrs8wyi3vvvffk/VtvvVWK6M4555ylz8jcDOyzzz5uxhlnjPxc6+IheCHM+HzxxReSBZrUCHvvvXeb71JrDwYPHizCHqU3+PdGG20k/54yZYpkkD7//PMlhQR5wXbcccdU11/kmOJ+LrnkEikubRiGYRiNSm6B7dxzz5UFdMEFF5QM6xSeVigyzWJ63nnnuYMOOsj169dPFvb2qP2qJWilgvXvwiCJajCRKiWMENhmm202d+aZZ4Z+b+rUqe7kk092f/7zn93999/vVlxxxZbPMFmus846bt111xWzKDlk0gpsRY2p119/XYTXrIWhDcMwDKMs5BLYMDMdf/zx8u+LLrqo1cLqw6JNmRx8zMaOHVuxGCp+WORSSkrc8WnPVcvvNCqYndGCoaHzhTUfsur/9a9/lWzSaMUWWWSRROcuYkwNGjRIBD7885L49BmGYRhG2cklsN1yyy2SrX355Zd3W2yxReyx+++/v9TsevPNN9t8RqDAOeecI8VSWWR/++0316lTJ8kNd9RRR4kTu8LijO/VkCFDxM9p9913d5MnT5ZaiQrvU1ORZMCcj8RzmMTweUIDFAYL/KhRo9zzzz8vCfm4JzREFG/1a43p7yNU4Lw/cOBAKQFE8kPqNvL/Zq8a8cknnyQ6Dk3ZRx99lKr4bRFjCiGNMcPr22+/lUoehmEYhtHI5BLYnn32WflbSWMGffr0kVcQBB1MXJjW8FdaddVVJcLzhRdeEMFo3Lhx7rnnnhNfKHj77bfdHXfcIWY2fJso6xHUbGEGw8dpoYUWkvMh0F133XUSzYjAFawdhq8WDumUu1h22WXFf4tFHgf7u+++291zzz0tPmH6+2iXMAvi/I5ZkZItfKdXr15ynu233z5TmzYCFM8FolIRggn2wIQaJEsy5iLGFNekUCtujTXWSH0dhmEYhlEmcglsCC8QZbZKAos+whoaFTRVOJEDWrbtttvO3XXXXSJkBaMBERLQaN10003yXXWkB9JA4Gi+1157yf9/+OEHqRmGMzymNEx6KuQhECKsodHjt1ZaaSV5/+OPPxazHteEvxTCoQ8RklzDaaed1qKBQ+tHUVmKvtZTYHvqqaekekUYCJ74geVhrbXWcptttpm0HeZHgg8QVIlS3WCDDSJ/OwlFjCnDMAzDaDYKEdiS+ieFQe4unNSJKFRhDai1iBCAEEW+sCDq8B5mbtthhx1ahDUguvDGG28UIQBt3X333SfCBZx00kny94wzzmgR1oBoyKuvvlqKHiOQEE2pNcz0nkeOHNnKXIoTPALbO++8k7k9iiAYSOCDX5lvPs4KWsYTTzxRhFNShGB+5oV2kVxtXANCdseOHVOdt4gxZRiGYRjNRi6BTYvW5nG2x/QVZv4it9cTTzwR+T1MolG+Ufi1BUHAQ4AgBQXmVgQ2fJ0mTZokAl3Pnj3bfAfT32qrrSZmNdJVLL744i2fIZAgnPgQqViGhL2YCaPSeqhpOS8I1MOGDROzMO2D8MwL7R7/58Vn+LFhok5KEWPKMAzDMJqNXNIFTt1ov9CKrLLKKpnPg+BECgYc/nmhBUNYi0vHQMqHKHzBygftEqgWB/83krIuueSSbYQvBa0cwgdaM/+8ZdYAnX766YnSehQBAir+fLxIlEsACVpRUoJget53332lfTfccEM5HnNpMBEumkw1IRc1ppJS6XoMwzAMowzkFtiAskSVIJIPbRVaMSI30dAAvmIEHSAUAYIGPlLHHnus+J75DuQ+aMWiiNK86fukpICffvpJ/sYlmdXfIdrQR6+/PfLQQw+JjyFBBUFBl8CRnXfeWSJl8UHEnxAfQBXY6GuicH0IDlGKGFNpqHQ9hmEYhlEGcglsqgG54oorJJ2F7+MVBL8xSkbhlO4vrCQ+RVjD7wwnfjQ1KgSQ4iELLN4EEQRRzRoaH0BLhg8a5s4oyCEGUVq79ghRtWjBSLKrEaNBaFeOQ2AjglYhdUocRYypNFS6HsMwDMMoA7kENsxGhx56qJgLibQkL1YYaDBwSAcWV4V8afg9ocUi7UZQW6MCVlqIBkVLF+Tmm2+WvwQSAH5taFMQ8DDF+kEHgDCAMInw4eeCa+8QlYvARjtHCWyA9hSI5k1K3jFlGIZhGM1ILoGNVBpEShKRSZQngQIkmvXBdMZ7L774okReklZDQRDCnIXgxnG+aZLF/sILL2w5Rxr4HhGmfhZ+EvOSJw0BQyNEAa3ekUce6Q4//HDxvSIHG2A2RcNDElfqWmLqM/4LQR233XabRIkijG2zzTZtjsE/kAAP2GSTTRKfO++YMsJhU8Jzga8oUb34c3br1k0CfsICPD799FMJGCGIhD6gnwkeIa9hFFm+0yg88sgjsuGjcgc+t0sttZQEPq2//vptjiXfo+YTDIMNz5Zbbpn5eKVZ2zvtWIU0/QPN2nbVuC8yJFCBhg10Nb9TT7Jeb9ZnNyu5QxopwM1DgqP7YYcdJsluSUzLA4OpccKECeKPhHM6n/mpOxDYEJ5Y/Lt37y5RnJjAiNyk4TSikZQcVChgAa8EPnAIgeutt574UmH2fPTRRyX5Lef286YBqTj4LfLBMajxaUJw5PjHH39cnNJV8DD+CxGyCG2YLXv06CFVJPAlo48QcBkPaN8QrNCY9e3bN9X584wpoy0EURD8QRAPCx7jm7FN2zG5k+eQBNAKUdTUZ/3iiy/k/7QzQUBXXnmllAujf4Jk+U6jwBgkiAZBANM7bfjAAw+IUEG76sZS4X4Z/1HwPPiTeNrjoVnbO+1YhbT906xtV4374lzkNGWOr+Z36kme683y7OahkBwUCEFkkydQ4JVXXpGXD7scHM/VFOnDDbPIYxpllwRoWShJdfTRR8sg4yEmX1oSgQ1NGNUJcHpXkxlg+sTsSs43H4Q7NG882CThJfmtf91XXXVVZDmr9gwTKMI2Jbo0jYcPPoTaf1nIM6aM/4fSYGiRiYSlTffbbz9ZBJnc+feTTz4pfeRPOmgymMTYQJGahSoWo0ePFvM0r4033th17ty51e9k+U4jwMJPjsb5559f5iENnsF/kmTczF8skgTYKATDsCmkPF6YRohqKj5pj4dmbO8sYzVL/zRj20HR94WGE+1cXLaGIr5TT/Jeb5ZnNw+FJQ3jgeDFwop2hPQO1PDEwT8ueSq7JTQmmsoBExdmS/VnQ4vDw6uVDBDaogQ3v2YkDzl+adS9RC3MtURB/jRqiZIEFjMbquQVVlghVHMT9/sQjDisJUX8NgMsScF0BicmB/qcoAJ8zmhrJk7amnQoeXPSZR1TPuya2nMB+PPPP1+irdGIoolQGN+4AKC1HDNmjPQffYY246WXXpLgDxY77UM2NDyjaD1ZGEkQrWT5TqPA/QDR6ix4CpU+SGPDXIAAoQIBY422ZGHEzaISaY+HZm3vtGMV0vZPs7ZdkfdF9RrWQ0zTSefOLN+pJ0Vcb5ZnNy+FZ3lF2IpzRI9Ci3WHkTWnGEEEwUCCOBAKre5kOhCs4/quCLKOKcPJJA5onIPwXOE6QNUK/DBYBNkgAe4EQYF7t912k4kfE4s/8Wf5TqOgVUFUc+OjEc1+CpoPPvhANnxLL710ovOnPR6atb3TjlVI2z/N2nZF3heCiM7ppLPyFSFFfqeeFHG9WZ7dvNQ/Lb9hGFWDdDRoF9BShKGmAA34QcMM5NgLwjnmnntu2VXioKta7yzfaRQwt6G5DkvUrSl//M8wkQCT+FdffSXO3zjOo+Vfbrnl2uR8THs8NGt7px2rkLZ/mrXtirwvP/cpri5JlBhZvlNPirjeLM9uXkxgM4wmBmfsKHAbwAeIiUUdbokyA0zbYfA+fjIcp7kJs3ynUQhGOGOWZ3KeOHGi+Nni5O6b73QSx9mbgCeOV3D/IFrd1yClPR6atb3TjlVI2z/N2nbNel9lJsuzmxcT2AyjHUK1CiKiSalDYIdG3unEHxV5O9dcc8nfqVOnthHY0nynEcF0QtS4gpkOIcLP+Yi/EGBi2XrrrcVUh9sAx5FEmnRDmGP4m+V4aC/trUSN1SBJ+qdZ265Z76vMZHl282ICm2G0I9hl44xNBPXvv/8u0WNE+gKmJVKxMOlEVZgg2TRoqbYs32lUuD8iD9HgoPEh16BW81A/FiLGunbtKn5D/fv3b/ku0Y9ENZNGCEf4rbbaSkxTaY9vT+0dN1bDqNQ/zdp2zXpfZSfts1sEJrAZRjuBFDVUkfj6668l2vbss89ulSOIyZ4dOp8TrRdWr5fqHzDvvPNm/k6jQlLta665Rv6NtgdhYtiwYbK7JpKZCXzEiBGR39eJnFQCkydPFs1P2uPbS3tXGqthVOqfZm27Zr2vspP22S0CE9gMo8lhEicFC8mgmdjPOussyWsVVn8VXxcmfl5hEz/vA+l38nyn0SESj4TaCBZMyjh9RznLK6TCIXKR46nDW2kSjzq+mds7zViNI6p/mrXtmvW+GpW0z3pSTGAzjCYGUwnVKEhMTSSUVg2JggmdVAm8SDbt89NPP4mZCdOLv1PP8p1GgPvp16+fTLzsloOgUUP7Q8JXFkTMdggc3GvYoqnfAaL20h6vNGt7px2rafsHmrXtmvW+ykrWZzcvhQls2MbJ80KiPrWX+6CiJvkhiQ813JoEqFQewO/ALxcFDLKkdb1wSGWQ0ohhD65C5mccLrE7a81QhXwqfmUEHyKTuFZqk/pOnfodsm83Ugi40X7gGWIBpN4rlTyifFwU/C1wmkXDEYzAo3wbY57SZJrYOut3GgESYuJQTDoEIr6CcxT1hjVSjFB+UiZQTo/5giTSVFHxwQFZ6w4S9p/2eKVZ2zvtWE3bP9Csbdes91VWsj67eSlMYKOA+pdffhlaBQCVIGUzsOUC6m2EK0KveUhJ6nfrrbe2Sr5KiCwFWZNAeSIENoTCJN+hocnfQ5JBhQ6o9F0EPkp+6D3SSUwwCKBxIem1JEvh5GYthGw4d8EFF8hfnrFKCyCweRo4cKBkRceRVhOUov2g/ArgyJ33O40AmzpSSBC2j2luwIABrT5nDiHqjglZ6x5vvvnm4uSOc3zQxwU/LDQgJIBl48jzmOZ4pVnbO+1YzdI/zdp2ae+LQAWUJ7Duuuua5i2GsLZCFsjy7OalEIHtsccec6NGjZLInCCEvhLu+tlnn0khcIQdNFzshvArIPMyuwI+o1ZcUFKlcTh3HEHfEbRdqNN92G0hmFBnlFIlffr0kVInXIsPYeHUX/NBEGX3wvsIdQiHaPWA2qOcA4EoeK5ak6VwcrMWQjb+q6XWGqya9T2KG264QWrDEv5PdNPIkSNlp84kr6XbeM5XW201mah8snynUUBzg1BALi80FWuvvbbMJdQ9pl4lggXPisLiyEaUtkD7Q3uwOX344Ydlc8fcRKFp3TylPR6asb2zjFVI2z/N2HaQ9r5oby3XxThjDTDCiWqrLM9uXgoR2CjMzsWq2tmHBR9hjd0PNUH9i1955ZVFeCI7MzfJzfnhscAuaosttkh1PTykUd/Za6+9ZDdy7bXXSjmPoJCFwBj23d69e8tO7YgjjhAhTQU2hEXMuji4+kWJa02WwsnQrIWQDSc1XhWNEosC7bRCFnCeU7QW7NoVTCpsnsLMKlm+0wggPIwfP14WQzZ7vBSEAzZCfvk7XCc4no0dkzkvhY0rFgXVfmQ5Xmm29s46VtP2DzRb2ynNel9lJeuzm4fcAhu7IqRJJPkgjz76qAhilAbRwdTmAjp0kEKsHIdZNCiwVQPCvBHYdEeXlL59+4rAhqqTXZz6TJCHBUGQ4vX1SkqYpXBysxZCNv7Lsssum6mwMRM7u0cyxT/33HOyCaCWK9m8i/xOo8CGEreOKVOmyHOBjy6uBlEJXNFmoKXmWcNdgudq+eWXb5XUNc/x0GztnXWsQtr+aba2U9LcF9q3JO2N9jJtv2T5Tj2pdL1xbZXl2c1DboHtsssukwcEISgIAhgggcaFZSONouYOOo1WC9SWMOuss6b6nl4f32eXp/eEuhQVNKZH8v7UgyyFk5u1ELJRDATYpDWVZPlOI8Czz8KXZlHnOUuzw057PDRre6clS/80a9s1632VmSzPbhZyC2z4CaChCSt0+sYbb8jfSjlIEBbIvVMriEACopHSgLYJMP36AihmRMylEyZMqJvAlqVwcrMWQjYMwzCMZiOXwEY4K6poMlKHobW28qia+Q0iM6LAR4F0Gz6ogtF2+WDCJGpy3Lhx4oSJzxbmwyB899577231HqVOcGhVjdQxxxzT5nvkDcIHj3w/UfXcqkmWwslWMNgwDMMwGoNcAhvCGuB8FwbCFkT5EiSBsORnnnkm8nPSfwRBmxQX3Yh5EHNfmE8dAlf37t1Dv4fpl4CDHXbYoc1npCRBKHzttdfcmmuuGfnbtSaucLIVDDYMwzCMxiCXwMZCDvhIhUH6Cxz0ybKcVctGhKIfQZQEIkvRdgVBU4YfF9oybPzkHQv6buHXRg06HwQ7MmajnYoq7aFtoEJQvalUONkKBhuGYRhG45BLYCM/GeDDFQaaNwQ2/KAqCWxDhw4VEypRmES25AH/MtJVhEH4N+bLf/7zn5LqImhuxVfLj7JMCpEkoPnM6kmSwslWMNgwDMMwGodcApuazMLMkoDgRSoJtFpEgkaB3xjO+mTZJzt1tSFnHAIbZUvi/OPSoG2gbVIP0hZOtoLBhmEYhtEY5BLYtNyHatqCkKB2+PDhYpY7/PDDIwv5kv6DbMIkOKyFw77+RpHaMD1XlAN/tUlbOBmsYLBhGIZhNAa5BDY1XZIwNgySIeL8T642HPkRzILVEDCDqgmSeqS1hAoMRYHZF1+3pZdeurBzpiFt4WSwgsGGYRiG0RjkEtg6deokAgrO+1FglsP0SCUDrWdGOSgc2okyJbcZggGmvLCkr9VAAwTSVjqIAxOr5i6rB2kLJ0OzFkI2DMMwjGYjd+Jcak2S8ww/NI0q9MGJn7xmFEhFeEP7o4lrAfMktS8ph1QrEByBnGxol/IW+yWx7OTJk6WiQz3IWji5WQshG4ZhGEazkVtgIwHteeed58aOHet69uwZegyCHDnAqHFGTjV8o3iP+pZodcI0QvjHpa1HxjmTfIc6c8Hj0LplrX9GUAV5zvr165fp+3nJWjgZrGCwYRiGYZSf3AIbVQZIRItZLUpga/mxDh3EIb7Z4N7RWiEI1oM8hZObtRCyYRiGYTQTuQU2oDg4pjOCD9pbRnwqG+CgP3HixHpfSi6sYLBhGIZhlJdCBDaKh/fq1Usy6V977bVFnLJhQFjFLLz22mvX+1IMwzAMw2hSChHYgIS35FuLCj5oRohuJXfcAQccUO9LMQzDMAyjiSlMYMNpf9CgQUWdriGYYYYZ2t09G4ZhGIZRewoT2AzDMAzDMIzqYAKbYRiGYRhGyTGBzTAMwzAMo+SYwGYYhmEYhlFyChfYnnjiCffzzz+76aef3q277rpFn760UEv0hx9+cN26dbPqAIZhGIZhFEqhAtsnn3wiVQ9+//13+f8777zjFl100SJ/oiaQW+3++++X/HKDBw9O9B1qoU6aNEmENuqnGoZhGIZhFEWhAhuFxVVY0/8fffTRRf5ETXjrrbfcU089ZeWZDMMwDMMoBYUKbKNHj5a/ffr0cVdddZVUPWhEgY3C5wsuuKDUSTUMwzAMw6g3hQls1NSkeDgJdM855xx36623updfftm9+OKLbrnllkt0DgqY/+lPf8r8eZrj4z7bZZdd5JXnWg3DMAzDMIqiMIFNtWs77bSTm2222dxWW23lrrvuOnf99deHCmxjx451l19+uRsyZIj7z3/+43bffXc3efJk9+qrr7qlllpKjvn+++9F+ENT9/7777vffvvNderUSXzLjjrqKLfEEku0nO+ee+5xl156qdQzxZfuhBNOEJ+y+eef362//vpu5MiRrmPHju7UU091N910k3vppZfcPPPM43beeWd38sknS9WC4LXhl7bpppu2vM/vn3TSSW78+PEijPL7+OzxW4ZhGIZhGNWiMIEN4Qx22203+bvDDjvIe7yGDh3aRhv19ttvuzvuuMPtuOOO7ogjjnAffvhhq2Pwhdt2223F+X/WWWd1q666quvQoYN74YUXRJgaN26caPTmm28+Of7dd9+V880555xijl1zzTXdNttsI99H4EMQXHrppd3tt98ukZwIfffee68IctQ+9YML9Nq6d+/e8t63337rNt54Y/evf/1LokC7dOkiAQYXXnihu++++1r57hmGYRiGYRRJIQLb448/LgLTkksu6VZffXV5D2EHTRuasSeffNKttdZaod+lcPrf/vY30Xotv/zyLRGWDz74oAhbvDdx4kQRxAAt13bbbefuuusu0YTtsccerc53xRVXyLm23357+f97770nwhXCHdf49NNPt2j8EN4QCm+77baK0aAjRowQYY1zjRkzpiX6dcKECXI93333XcbWMwzDMAzDiKcQgQ0NFqh2DdBabb311u6aa64RLVuUwMZxCGa+SRI+++wzt84667iDDz64RVgD8rv16tVLBDaiOYPwmyqsAZGenAdtGmZU3zzbo0cPN8sss7gPPvgg9v4wzZ511lmiASTy1U9VgtYNk+hhhx0Wew7DMAzDMIys5BbY/v3vf4tGC3bddddWn2HuRGDjcwQeTJpBOCYorEGU4/8vv/wiyXmjUA2fjwp8a6yxRpvP5phjDvfNN99Eng9ef/1199NPP4kv3LLLLtvm8z333NMdfvjhEohgGIZhGIZRNLkFNhzwv/zySzFl4rzv8+uvv8rfzz//3D3wwAOtHPgV0mdEgQCEsPT888/LC7OmVlKIYqaZZor8LGtCW9Xk4QMXBqZffOk+/fTTTOc3DMMwDMOII7fAptGhP/74o7vyyisjj8MsGiawYZIM4+OPPxb/Mko+AelCMKsee+yx4ux/yimn5L30xBDFCjPOOGPkMVH3YRiGYRiGkZdcAhu+XfiSAYEBfpoN5ZFHHpHUGTj4X3TRRbFCj0+/fv1EWCPalMCEtddeu6VG5y233JLnslOz2GKLyV8CGMJAE1jJD64eJKnrivaQwJA0dO3a1c0+++xFXKJhGIZhGAnIJbCRHBeBgEhO/LvCIILywAMPdF999ZW7++675f+VQKNFIAJaKzRzwWLqpN2oJQiiBBwglOLvht+bD+ZeNf+WhaR1XUmRMnz48FTnfuyxx0SATgLpVPBjJCceAv5f//pX17dv39jvY1o+99xzpTwYPotEEe+zzz6S2sVID24Lzz77bOTnPL9bbrllq/fYaN18882SEJsNCbkR8TeNes6hmfstbXukbQtr78qwsbzgggskByZWlmWWWUY29KRpSspll13mzj//fFEehPk7NzpFjYks47GI/qklXC9puXC7wm2LtYlrxXc+T1L8ao6xXAKbRoeiQYtiuummE9MmN4HwlURgm2aaaSQQAcGNNB6+Vg5TKY0MfFYL5p13Xhl4N954oxswYIAk6FUhEgGujOW3ktZ1RXA65JBDWr33xRdfiKkbf8C99967zXcWWGCBRNdwxhlnuEGDBokwyzgAhD2ERPwdMW8HIc/eRhttJNcABKqgKcTczgNAgIeRDtrtzjvvjPwcAdoX2Ih4PvPMM2WiRjvL5MWmhOeOZNL6/Pk0c7+lbY+0bWHtXRnWDlI4IYSwPjCfPPzww9I2e+21l7vkkksqngNB4qCDDpJzIFA0G0WNiSzjsYj+qSVXX3213AsKJ+4PGYP0ZKxNCLykDCOxflqqPcYyC2xocMiVxs1S3SAOPkdgoxpBmIYqCB2Ovxv50cjnxkBgAKClQVjSZLkIUAsvvLCk/qg2VDjg+snzRpWEzTffXDqFXQhJf6k7yvWVhaR1XambysuHQcf3Cabgwc3CQw89JJGzROjycJBuBUhIvP/++7vjjjvObbLJJm611VZr9T12N0w49DlCHdfAtfAdXqRR6dy5c6Zraq+8+eab8kxR5SNs5+hHPjMxI2hTIYR+23DDDeV9kkMTBc7Ez6IQ3Hg1a79laY80bWHtXRmsAyz6ZCRAAGCDgSCBFohUUqwJ+DfzfhTM1axD/G1WihgTWcZjEf1TSz766CNxs0KRcNppp7n99ttPBDYEXv5N3liE27hNbhi1GGOZBTZKTv3xxx+ioak0CFAzImRNnTpVhDD80yrBwCAZLaZROh6I8iSXGoIHDcqAQpCqhcBGhOgzzzwjamES6PICtG/45/Eqi8BWRF3XvAwcOFB2aKjI0U4qtB/Cd8+ePUVt7Ats7HAQhldZZRXpf00Dw04IX7vTTz9d+hxhz0gGfcCEyjOKAF0J2h0I6mGCVzbbbDPJN8izxkTmT9jN3G9p2yNtW1h7VwZXGtIqIRRwjwrrCgsuiyR+zXECAVoj2ow5kawGzUZRYyLLeCyif2oJ6w7aL8ph+vlTV1hhBfHJx/xLcnzmTfVfT0ItxlhmgQ3TIK8kYD4Mpryg4+MELdSRVBFgsOGzhhkOm7iaItF0MRg0VQcSM68wEC55hREWLBB1bXQk6UW4F+qeYjLERs1uAo0bO4kykLaua9FgyqZ9aBcEsyCYyNGyoiG9+OKLW/Lw0aeAiT2Ys4+dGpMO6v1mWYhqAeObHV9USpog+ByC7qx9WAzgjTfeaPV+M/db2vZI2xbW3pXR+2f+D6La4WAb+SBgsHHEvQOXGsxdzUZRYyLLeMzbP7UGoQrCLIMIW/h+YwnC7zepwFarMVZYLdFqgcN/WPQp0Lj1AHUxr7KStq5r0SDQ4l9IG4UlS4ZOnTqJ1o/BrQ8FGkCgzmsQdj9zzz237HpIIZM1p157A3MoILAR+IMzMg62OCMjvAejtjGHYNoIy4+oUdLBz5q539K2R9q2sPauDCUP4dFHH23jb6vWFz0mCOYvTIQ4lOPegYa/GSlqTGQZj3n6px4svvjioiGkXcLQPK9JM1rUcoyVXmAz0pGnrmtRoA1F+4jg9vXXX7cqLQY8EJqMGF9IFdhUCxslDPM+Phocx0NnVEYFNpyPKdNGpK6CFhuTub/TxK/Qh+MR9IiQxh0BrWmwDFsz91va9kjbFtbelcGFBlcaXlhRMGUxv2CBIXApLGk74LLDppU25di4pOqNTlFjIst4zNo/9SLOLxs/Nvz4ENaSRHjWeoyZwNZk5KnrWhQ4uKNWJp3E8ccfL1E3Cj5VRxxxREsaFAQ2RSedoICnzDXXXPIXX8hmWIhqgQrG+FwyBjB14FbApITfJXV56RP+Bvn2229bBQih0eZ7wfHTXvotSXvkaQtr73BI74TTOzWhMTvxUmaddVaJPA/TlpCuiOAnzIErrbRSLS+55lRjTCQdj1n7p2wwVnDXwaUHQTNJlGitx5gJbE1E3rquRXL22WfLQ3reeee5V155RXZuPAjY9hEeUNGz40Pzp9eOGRVhQlOABEHwBCYSIxkIzyQ6RoDv379/y/vshOkbQtDx18TPMWgqoR8YR+yw2XkSDY2PBoKe+sS1p36r1B5528LaOxw2d7QL8wauFOQCQ5PB//GVJTqSeQUNskLSdZzkmXcOPfTQ+l18DajWmEgyHiFL/5QJ1iHGCv7UpMIiohZFQyXqMcZMYGsi8tZ1TQu7r2DCYCKRtt9+ewnQwKcB9TjpX3gBO0AeXnzp2HlpTjcmBz7DhEoET1ipL1LCAJG5RjJGjBgR+ZkKbSSOZGIN7pyZdBHyAWGbyWnYsGGiqUMI13xL7aXfKrVH3raw9g6HDQVRhgQwMb/4ZifMWwS/4faBMzkbUbIL4HzP/ERKo2r77Nabao2JJOMR0vZPmWB8IGzRdiSWR9EQTCIeRr3GWLlaz8hF3rquaUF9zO7OZ6GFFmr5N5odBAGcXXnA+QxHdx5aNDvgJ+HFz4IHh1fYpMP7we8Y2WGSIfILgY0AkDhTOX02ePBgmZw4HidnNXO0x36Lao+i2sLa+7+QLmLUqFEiHBCFH/QRYrFlPiPlEj5EpJ8gwo85Z4011pDcgz6Mc8Bsx8aRY5ohEKHaYyJqPGbpnzKAYEu/k1sVYRerEznY8NFLQr3GmAlsTUI167pGwYNaCR7kYKQvkwcBEOz21LcCmEwIK+flC37AxIBKHrV/s2gOqg3qfSYm2ixsEgfdJWOipt1xIEaIQ/MWdiy7UKKidAGAZu23LO2Rpi2svSuDzxWbQvIIRvlnITggEGgUIz6ZQEQ0rzBwkAfyeTaDwFbEmMgyHrP0T73BfNyjRw/J8YowpQn401CvMVaYwIZtHK0OifPUXh7ks88+a8mHtuaaa7bJcq8wwJLmNEPLwwBlcQobZAq+UjhbovUJ7gLIU4X9OgyEGiIuqWTgD0j9Dp1RhtD5atV1zQqRRAiIBBzwUPjwgPCQYy71wY8Kcy27nmC0EiZV2pyqDMHaskY4aFpJWM0YJrhD890pTDpaYxTNJ5M+fifsHIkeVWFOISJKo05JC6I0a7+xCKVtjzRtkeX8aX+j0WEhZfyS/of5LWyTqYE16lfFvSMghEHaCVwxSJ5KFCAblWagiDGRZTxm6Z96g2yBsLbNNtuIT3eU318c9RpjhQlsRx55pPhPxSXDRaAjAz6QLwYVaRhoi4L5XKLo0qWLCGzY2JN8hwWMXDN+/VMWtkrfReDDL0zvj8WPTmfXkLV8U5FUq65rVnAwpZ1pM4RDtfGTBJn3+D+ZsX1wXGV84AeBg7ym+2BHpGrnsNqmRjiMWRI6o1HFiTboz4a/BrtqInrZzNAnTDCkAMFEEEyMTX+yo0a40/Jw0Kz9pomx07RHmrbIcv60v9HoIGCwAcU/l7QStJPvL0TCUmpWzj777C2JXYlmjMrRqVGPCA96fDOQdkywYSabP6y77rqiecsyHrP0T73RKFYiO5MIa2FtVa8xVojAhjSJeYxIkjhUqEDYQeonFDkuAS0NU8nsFgwXRtuFBseHnQG/heDAAKK+Jk7xaNt8aGj1A1MQQtm58D5CHcIhQg8MGTJEzkEUTPBctaSadV2zgmqdB2PcuHFSvozdDMItamIeejRwwfByzKP4to0cOVJ2iUwwPOhoZRljaGQRQIzkMFljIqdN2T3TrmijmUTZcPC8UJhZJ1l21kza9A9jir7j+UFbSug+E1zQP7KZ+y1te6RtC2vvyuC+gYWDtiIyDz8o1hD+jS8RYO2gDdoraccEVizdsDMPUB8UsozHRuof7ht/aqgkTN1www3i6x3VVvWgEIGNep4MEl9tH4QIEQQ6SlVgDkVoQLCK08gh8W+xxRaproUBFfUdNDrsRBAcKeURFLIYZGHf7d27t+wqyB+GkKYCG8IiuWdwxkxbKLZIql3XNQsIAjhcYjJGYCBhL5CXhwhRdmNhUMMO4YGdmmpjARU0wnszmHlqCeZ8dr9sNugHXgo52TAP+OVXmMQ4nsmfDQ4vhfGFiTss31Cz9luW9kjTFtbelWFOe/rpp8WBnfZBEFDQYmDhKIszez0pYkxkGY+N1D8klVc0cjYKrHZlI7fAhrSK1BlVq1NRzRX5oBgUaparReF2H0KSEdhUyk4KhWsR2DAhIRypfZ/7QRDE1FevJJV567oGQahWp8o80B4kFcQngsgiHN/p+7hs0FwfWiEEOgrYkzaEGnVlzeHTCLC7xsxBP6DlJOILX8co7SruCkQ6TZkyRfxP8Eml7EpcIslm7re07ZG2Lay9K8PGgw0gzu7Mwbix0EZBB/tKaGBWM5JmTKDtiprjs4zHovqn2mRZ2+LaKoxqjrHcAhuCl2bSj4KbRaBDyMHHCudmOh+pvNaCDuYgQNOTBhXQ+D6St4b/oipF/Xz55ZdLjhqjLWhwkhbRVQjwqKfquRlJ0w+Mdyb6tAJAs/ZblvZI0xbW3sngfqtdqaXRKWJM5BmP1j/VI7fAhl0brUlcigjs30jrmGBU4sasiF0bQY4yELVCKwHgU5UGnDkBs6+fqwXHbsylBFCYwGYYhmEYRjXIJbDh7I7qtFJZBg028Msl7bDDDiKw8VmUwMb5icqIAns6zo4+qIHRdvlgwiTDPw7wOGDusccebVJK6HfvvffeVu+RAgPnS3ze4JhjjmnzPdJW4LgdVujcMAzDMAwjL7kENs3oi/06CoSgm2++WTRwlK5QCAUmCvS1115zkyZNaiN4ASHJUblOgPQfQcgFg6N7FKQwIJw3rJQEAhclNMLA7EvAAYJmEJLCIhRyLwRUGIZhGIZhFEkugY1IQ4jKRwKaPmLVVVdtiRRUyKGG9orggzCBjegTP6ojCTi0o+0KgqaMEGN+D/s+2YmDdc3wa6Nemg+CHdmdCXWOKuuh91/Jmd8wDMMwDCMLuQQ2cpQBflxRaHQoOaCitFf4sRHdUkQBVfzLyIsWBqHKmC8JO0Z4DJpbSUVB/pm0aH6ZL774Iv0FG4ZhGIZhVCCXwKZ1IMNMk4BmjbwsCFFovYIaLSBVBnXOHn30UTFXVhvyxSGwUWIjzj8uDXr/fl1MwzAMwzCMosglsGl5CtW0BbnlllvEh42UH1QXCIPUHmRIxixaC4FNgwKK1IbpueKqNhiGYRiGYWQll8BGUj4gl1oYGh0aZaIEqtgjsBGYQNRnlkKsWaAQfVGQkBRzblmK2xqGYRiG0VzkEtg6deokQgoO/EEwc1KvEEd+SmNEQVTlwgsvLHnaSKkRd2wRaIBA2koHcWBipUzV3HPPXdg5DcMwDMMwlNyJczfeeGPJe4bpk9QXCiZOKhyQIDcuqS6aKVJlnHbaafKdagtslOkBcrIRwZq3SDIlOCZPniy1Gg3DMAzDMKpBboGNJLTnnXee1BHz86wdeeSR8krCyJEj5aXgG5e23hfCYpLvUN8seBxat6y1M0kVQqmqahVRNwzDMAzDyC2wkT+NYAFKN/kCW3uB+950001FEDQMwzAMw6gGuQU2OO6448S0WOtC7vWGygYk4p04cWK9L8UwDMMwjCamEIHt73//u+vVq5c7/vjjWyJD2wMIqpiE11577XpfimEYhmEYTUwhAhucccYZUsw9GHzQrPzyyy9upZVWcgcccEC9L8UwDMMwjCanMIENx/1BgwYVdbrSM8MMM7Sr+zUMwzAMo34UJrAZhmEYhmEY1cEENsMwDMMwjJJjApthGIZhGEbJKVRg++mnn6S81JNPPuk+/fRTKbS+1FJLSfmplVdeOfJ77733nqQEoTZpx44di7ykdgUpRpIkAKZeK7nz3nrrLff++++n+o2uXbu62WefveX/H3zwgRs/frx74403pD5r586d3RJLLOG23nrrVsdlJeuYStoWQC5BLVlmGIZhGGWkMIHtwgsvdMccc4z7+uuvQz/faqutpJoBi20QUoEce+yx7sorr3R9+vQp6pLaHSTwpepCJah5+vnnn0tJseHDh6f6jccee0zSmPzxxx/S32eddZZEzAaZa6653AknnOD69++f6vw+ecZU0rYABE6ONwzDMIyykltgQ4ux3377SUoP6oLuuOOObvvtt3eLLbaY++qrr9yzzz7rzj77bDdmzBj5N4XSKRpvVI999tkntn7rzDPPLH8RvII1UL/44gs3evRoN9NMM7m99967zXcXWGAB+Tt48GAR9tBM8e+NNtpI/j1lyhR35513uvPPP98dfPDBUmaMMZGGIsdUpbYAtIKGYRiGUWZyC2wXXHCBLKyzzjqrLNQbbLBBq89ZyA866CC3xRZbuIceeshtt912Yt4yqsfQoUMTmfj+8Y9/yMvn5ZdfFoFtttlmc2eeeWbo96ZOnepOPvlkybd3//33i0lRWXjhhd0666zj1l13XTGLHnjggakFtiLHVNK2MAzDMIwyk0tg+/bbb91RRx0l/z7nnHPaLKwKGo7bb79dFvOnnnrKvfjii2655ZZL/XtoXtC41PNYw7lnnnlGTKJo6HxhzQdzJfVVKd+Fj+IiiyyS6Ny1HlOGYRiG0QjkEtjwOfvhhx9cly5dXO/evWOPxQH9pJNOco8//rg4uydZXL///ntZtPFxwzn+t99+E9MXpbBY1HFu92HRHjJkiGhbPvroIzf//PO7NdZYw5144oltfi/NsUZrPvnkk0THnXvuudK2JBlOSrXHlGEYhmE0IrkEtgkTJshffJ2mmWaaisfjLxX0mYri999/d9tuu62Y3DCNrbrqqq5Dhw7uhRdeEGf5cePGueeee058pOBf//qXRD7iAI9mZ+ONN3Zvvvmmu+222+Q6n3/++ZbC9GmONdpCNC8QiXnKKadIeS5MqEEQrNNSzTFlGIZhGI1KLoENgQn+9re/FXIxPggDCGvLL7+8mzhxoqRzALRs+CzdddddbuzYsVJ8HYgmRAC76KKLxNEcMHUiTBBtiLaHiMa0xzYimAjnmGOO0M8wJcalw0jCWmut5TbbbDMRminPRfBBr169JNISE2bUbyeh6DEV1xYw7bTTimbVMAzDMMpMLoHtyy+/lL9LLrlk6Oc4hoelVlhwwQVFaIqDnF44rxNpqMIaTD/99CIcILBhBlMwccJuu+3W8h5+aYcddpg4x/sCQJpjG5FgIIEPGsVXX30192/ccccdYj6+7LLLJEUIQQK8EIDI1cY1IEynzatX9JiKawtAmItKG2IYhmEYZSGXwKaJSf/973+Hfs5iHpajC0f1SgLbLrvsIq8gnO+JJ55o8/5CCy0kiVXRkpHTTU2a/A1GO6Y5thEhl11UKgs1IecFwXnYsGESLUpaDbShvNBo8X9efIa2UrWYSSh6TMW1BVRK+WEYhmEYZSCXwEa6BAQf/L+CAQDwwAMPtMo2jzlzww03THx+vvv666+LTxkvzGUIaz///HObY0eMGOG23HJLcVq/6qqr3CqrrCKpJUj9sP7664v/W5ZjG5HTTz+9ZqksaCuiRXmRKJdAEbSfCL5Ek+67776iLdN+R6P166+/tjrH1VdfLXnWoOgxlbYtKl2fYRiGYdSDXJIJvlD33HOPe+mll8SnKQi+Tj4cl5SPP/5Ygg7Q1ACLLudDI0YUIc7uPt26dRNTH35p5O5CWOCF4EBKiWuuuUZMrGmPNdpC7jMEJYIKMIH6ECCy8847u5122kl8DUm9cd5557UIVfRpUHuGxlOp5phKQqXrMwzDMIx6kEtgw8mcxRWzF75FldI3qPCVhH79+snxO+ywg5gu0eCocHDLLbeEfgc/JlJ18CL1BCa6Sy+91D366KOuZ8+ekhpErzHNsUZriODEf5AkuxoxGoQIT45DYHv33Xdb3h81alTsuas5ppJQ6foMwzAMox7kEtj69u3rjj/+eCkAfsYZZ0jEYBQ4dmMySwJO5QhQs8wyi7vuuuvaaHEoFO+DNo6akghhBA4Azu4EFeAHh0nunXfekQLl1NFMeiwRqkZbaBcENrSTUQIb0C+QJoijWmPKMAzDMBqZXAIbubeo6cgie9xxx4k/04ABA9r4gJHtnohBfJOSgHYGzQqCG6Y33zEcIYDUG8BnQAJVEuzyu2jkfBMW/m6YuIgCJSv+dNNNl/hYI5zdd99dctYRJYowts0227Q55sMPP5Qao7DJJpskPne1xlR755FHHnE333yztBs+gEsttZSUDMNnMwzaFS0nQSQEedDPBI+QDzGKLN9pRMj79+OPP4pGPozx48dLjdso2PDgQ+tj7R0NaYPIy1kJAo/wQ46DoCXqHOMOs/rqqxd1iaWhGmOi0nhXsEqxNuN3TuYAMhLgfoQipIyVhKpxvUnbKiu5veuJwqP0EIv3wIED5WEglQK+YGhASKFx3333ybE33nijHFMJBDZMYwgF3bt3l4UZQWvSpEnSEBrpyPkQrEj9gRmTBQnfMxZ7KheQGuT6668XbQ2pQDQfV5pjjbbQvwhtV1xxhevRo4dMfKuttpr0xXfffSdCAdo3BGqc9WnjNBQ5pujjSkEkJE5Gm9esoEnGPxNBjeheJiOCN5isCArRDZBCcmrqtX7xxRfyf9qPYB+CdFjo9txzzza/keU7jQj3d8kll8Qu9uobGwXPgy+wWXvHQzWTsMjwINxznMCGCwduFpwLP+hmoxpjIsl4BwKzmEtQejC/oGShAg1J7hEgyZk6zzzzZLqvalCN603aVnkoJBwSsxQXefTRR4tQRfFuhcbA4ZwFkZ3l3XffLRGflWCAsfhjGkU7ADPPPLOUpOJ3GHw0Og8zApvmALvpppsknYQy00wzuf79+7tTTz215b00xxrhMLARqjFfahoPH0qIaT9loagxhfBYCXZWzQqCGe3EpoTnRYM/EHh33XVXec6Y5AkQUdhhMvmwUeL5QOs5evRot//++8sLAbdz586tfifLdxoNduJoK8Ki1H2IcGbTyTwStlNfdtllW/3f2jseAsziNGxs2qheg3YkCoQ0AqGSCH6NStFjIul4p/wgfuZE15922mluv/32EwEIAZJ/U/6RdSBuE1NLqnG9SdsqL4Xlr0ATxgvfJjQgaELwFyNlBou3EubUTf6sYA4tpFvKFHE+fNYWWGAB8ZdSfza0OzQ2QhyQXBcNGRUK8EEjASvfwSeNyEWfNMc2ElG5y9LAYuKnzYiChQiTGgs9QQW0I8EbCAaLLrqoW2yxxXKnR8kzpopoi2YAgQxY9JiwFSJwEYrZ7DAxqcDGLpPIW9qY72ofshulH0iTguCHuVrJ8p1GAj9K5gtMKJWeDT7nWWBhPPzwwyue29q7MnGl59jM0T9o5cPydipomWkzsg1ocu5mosgxkWa8AxYQNJZYXdQvHFZYYQVJ8YT7xZgxY+S5YF2oN0Veb9q2ykvhCcfInRWWP6sa5wvLr4W5NGly2DTHGuEgQBfd50Gqff5mRqtahOWqY3IHAmwUNkJAapagwE1gDhM/JhZ/4s/ynUaCiVjH4LfffivanChwqUCLs/TSSyc6t7V3dtBmIKSxQWQRjoINCRp6otbxgcbc1WwUOSbSjHfQ1EpoMIOwRlO3m8o4+HWWQWAr8nrTtlVeGjtDrGEYsWAORdtIVHQQ/ATB/0zLtpFjLwg7UDSc7DxxrFXtdpbvNBJ+zkdM/3G1ZzGHAgLbV199Jc7fODTj/L3ccsu1qaxh7Z0d3GPYkNAnUfeJ+QsTIW4P+HFiFWhGihwTacY7UCEIDT2/E4aaCctSVabI603bVnkxgc0wmphghC6VKBAkJk6cKAseQQi+WUCjbjFth8H7+MlwnJZ0y/KdZkUFNpy9CZKhvRXcPIhQ93f21t7ZwDcVrRkBYlERkH/88Ydol+gD3GvwUW5W6jkm4so54heGHy3CT1michvten1MYDOMdgIqez/6GfU/k5NfPUInfvw8w5hrrrnk79SpU9sIEGm+06zgLwSYRrbeemsxReM2QDuTRBoBAzMKf8HaOxtEhtOuQ4cOjTyGdCBUZcEcuNJKK9Xw6mpPGccEbU/lGNJzUaGoTFGiYTTC9ZrAZhjtBFLjEBmKho2dJLnytBoFJjxMp6RiYSHk2DD+/Oc/y1+EP8jynWaG6NCuXbuKZoeIc4WoNEq0kVaCQI+tttpKtJvW3umhGg1O4QQjoMUMA/MUQTVomA899NDaXmCNKduYQJNH25ONgeheIlTJJlBWGul6TWAzjHYCJiHq5AK7SCapYcOGiSbolVdekcmeHTrRuERRUWkkyDfffCN/5513Xvmb5TvNzIgRIyI/U6GNFACTJ08Wzaa1d3o0XQrtGQbpoHC+R5t81VVXlTJpa5GUaUzQ3gjIXAvBICRBDyaJLhONdr0msBlGO4RIMipRMGEhQOC0jBMuvi5MXrzCJn7eB9LgKFm+0x5BcCAyl/YmiSsCm7V3OgiUGTdunFToiIocJ8IPB3scwIM5NWl3wP+NaFGOaYZAhHqPCQRF2pE60AiPpMwipxla5DLSaNerFCawoWolbJi8L6p+DfLggw+K+YU0AjiCEjKLKYZ8KGFRbD/99FPiEg/YnikzhUqTXWwUJBPEho/ZIuiESjg+atEwcEIkTxvlT3w/Af0OifaaOSLLaDyIoOvXr58ICWHPBOY7dpVE0vkTOt/j5ZdtA55HzKiYXvydepbvNCPMPSwE3GvYogm0ORC1B9be6WCuJZiAyM8oNB8WEbq8wqCKDjBvN4PAVs8xgTmWijckuUcA1gpEZaXRrtenMIHtyCOPlISE+GcEIakciQ0ffvjhlveoFUpGYcBxFH8EQmR99TVCXVzSRJ8uXbrIQMXUk+Q75F8j5QGqc4WQ50rfReAji7TeJ/dBx7Pzi4s+MYxaQ/JWnN/RNhCdqMKCwsKnUY2knQB8q3CQZ+cZjDBlw8UGhTJhmsA663eaEeYP5hU2dySRZm7wQZDQGqOk+ABr7+QwXsk3hhaEDXoU3PszzzwT+hnz+2OPPSZ524gCVMG50annmECpwhpITWmqB0X50ZWFRrten0IENh4Ass3jyBxkypQpbt1115WEkpQRopQUD0rHjh1lUrvhhhtEYEN1HRX1w64gLJu9TzCnCtouJGcfHniiaShlRDJFhEiyGqNt88H3gZIePgijPBC8z0OPcKiTxpAhQ+QcJHEMnqvWpC3yDe2liHR7Aw0yzxopJlD5DxgwoNXnbFiIGkN40ATSBCUQgUdWdJzmNXEku1I1LxGo4JPlO80Im7nNN99crAg4LQf92fCPQQNCYk6N1LP2Tg5CGON17bXXjk3RQfRzWFJ10ChpLDuaOLoZSDsmCFQgcANYn/No3rRsING4jSD8pL3eItsqL4UIbAhhSPW6S/fp3bu3CGsIDeyO/GR0CG04/JHsj4bAAZpi4ZgdfXg444r6hkFHRH1nr732kgF+7bXXyjUFhSx2xmHf5V5Y3I444ggR0lRgQ1ikyDg+QfWsl5a2yDe0pyLS7RE0awhtjA122ix2bFwQ7KknynNCXyuE/xPJOHLkSHmmmeRnn312Kb/Cxmy11VYTocQny3eaFRZHctzRFmg3aQ9MpVgX2NWzkaRAtFoSrL2Tg+8asFYYrUk7JjCTajk6xiVrQBY4DwFLUEkARjlD/el6kuV6i2qrIsgtsHHz3AQDIwjvM1EhkV522WWRmYMRgjAxYmpEiAoKbNWAyDh+SzsvKX379hWBjZ0yC5+amQjjRxCk7mk9ch9lKfIN7amIdHuESWn8+PEymaNZ5qUgvKFZDeaoUtcEtHLs2hVMKmi6w8wqWb7TjODnSnujhUdw46XwTGKOCZa7sfZOBu0KJrCFU48xQR1pRSNRo8Bdqd402vUGyS2wIYgRZIAAFIQINKCwe5QTroKmjQkNgaEWsOuFtMXeVUDj+3SoRpUgCLGrufzyy0VTWGvSFvmG9lZEur2CBpvoONwT6FeeV0r1RCWGZGJHU0QlhOeee879+uuvbplllonMeZX1O40I2spKRZ7RZqClxncQ31aeK9xB/KTFPtbeyVCf5zxQ3LtZSTMm0L4lKVZeabwvu+yyNSl6XhRZrreotiqC3AIbGhwW/DDtGapYCCs8HYTJLM7PqmhwNgQcD9OAAAOYf/0QYARNNIWUQKmHwJa2yDdYEen2AxsNJu40CzrR0GnV/1m+06ygSUtT7Nra2ygCGxPNSy6BjaABdu5hmaSRNNnRo6INMxGijsSBNAwcQoO/E6cGx6wTNKOyu0Db5YMJk0LM+EIgTGIGJKVIEL577733tnqP7PD4AKmQg9YwCCHC+KeQIiGqREi1SFvkG6yItGEYhmE0BrkENk1CiN9GEBz1EJAwOYZp3/AfO/DAA0PPi6nRt7cT6RIVpg1+gWXl559/jnWYJ1ILDVJYFmwEru7du4d+D3MSAQc77LBDm89I5Mg9E6G55pprRv52NUhb5BusiLRhGIZhNAa5BDbVkIWFUKORIQJNBQctPqtgPgwKbITOopULgtO77yyYBCJL0XYF4VrIhI22DLUxqSyC5kCETPy+fBDsSDKKnToqW7S2gwpC9SJJkW8oY8FgwzAMwzDakktgIzcZRAUKsMijbcJ3CnOhDxouXj4U9Q0T2LKARokIyDCImON6KBCMI2vQ3IqwGdRGJQHnRNAUGfWiUpFvKFvBYMMwDMMwosklsKkGJswkCTjAI7DhuB4U2ILgN5Y2xUYeMCEisJHpvagwcW2HoDax1lQq8o0DepkKBhuGYRiGEU8ugU2zo6umLQjZ8skqjPM/eYlIJRAF4chofWqFmgGL1IbpuaJ8wupBVJFvqHfBYMMwDMMwkpFLYCPHC5AsNgxyDyG0UbB3gw02kECDYNoJoklJ6odQUQ8+++yzws5FRCW+bsEo12qTpcg3tOci0oZhGIbRSOQS2Dp16iTCCY77UZB1mdJUFKUloSuCG4IF+YkQ9HD+pyByjx49xAfML5NTTTRAoEgzLCZWTYdRS7IU+Yb2WkTaMAzDMBqN3IlzEcIweeKDpk7qPtTlJMM+udIweyIg8FIwq/IZZZCo3VUrgY1s5EBONgSWvLX3yFU2efJkMf3WmixFvqG9FpE2DMMwjEYjt8BG8lnMcGPHjnU9e/YM/5EOHSS5LuWRKJnx/vvviyl04YUXlsLrqhEi4z4vBeEibakHhMYk38GfLngcWrespSVIFYKDP6bJepC2yDe01yLShmEYhtFo5BbYqDBAeg60NFECm4JghoDGq9ng/jfddNPYwIpqkqXIN7THItKGYRiG0WjkFtiAWpNoYvBJa48JVkldglaLqgL1JG2Rb2iPRaQNwzAMo9EoRGBDUOjVq5c7/vjjJRK0vYHAimkYTVa9yVLkG6xgsGEYhmGUl0IENsCxnfQdUcEHzQqRlJgaDzjggHpfimEYhmEYTUphAhsO+4MGDSrqdA0DUbDt8b4NwzAMw6gdHYjKpDSRUV+o8vD888+7jh07tkliazQPRCGTM4+kxQsuuGC9L6dp+PTTT93nn38urgCzzjprvS+naSDS/JlnnrF5qWCYA8iCQKYEIxnUxsY/m3GoeVTbAzvuuGNLXfQO66+/vpj1jPpC7rMZZ5xRFvH2GLjRXkBgI8UKAtuSSy5Z78tpGqjKwYvE0KSmMYoBgW366ae38VowzAEIbLWuitPIUPrxjTfekPXRzyfa7Gh+VOhA6SjDMGpHPZIrG0ZWyKFpFAs5SQ0jLYX5sBmGYRiGYRjVwQQ2wzAMwzCMklMqgQ2nYXwm5p13Xsm+b9QfgiE+/vhj6RN87MLA/+7rr7+WdC5zzDFHbS+wQD777DPxMbPxl50k48WoDjp+25N/T9mo5Rr2008/ue+//z7x8QTjUHe6UbHxXSKB7eeffxbHVgbUN998U+/LafdQFxXflUsuuUQEsksvvdTtueeeEt1EGS4YPny4m3nmmeX/e+21lzvwwAOlBFYj8uOPP8r4m2222dyXX35Z78uJJawP6k3UeDGKJ6z/2TDNP//8sph98skndb7C9kmt1zAS1Z9++umJj7/zzjvdVlttVcUrqh5lHN/1mIdLI7BRFolJf9VVVzXtRgmgVNV5550nESrdu3eXahZw2223yfs8OCqc/fOf/5S/FItvVEhd8Pvvv8s9lH38hfUBu/revXtLpYurrrqq5vcQNV4agXq3XVrC+v/pp58W7cPqq69e56v7fxqtXZMSdV+1XsN03iWzQBLLRiPPz/Uc31H9HfYcVpvSCGx0CDTyoGoWqFaBhoQ6ow888ECrMleo/KlPut5667W81wx910j3ENYHr776qpSFW2WVVWq+MMaNl0agnm2XhbhnsEwCW6O1a1Ki7quWcwibSwREuPHGG91aa61V9d+sJ/Uc31H9HfYcVpvSCGy6WyjThNNeIYHvd99958jRF1x8L7vsslb/x5RIwXlyXy211FI1vMpiaSQtYbAPoJ4TWtx4aQTKKOzEEdb/ZRy/jdauSYm6r1quYS+++KL4sJHPjdKIzU49x3dUf4c9h9Uml8BGokoWa6Dw+SyzzNLy2Xvvvedef/11+feKK67YylGQgfboo4+KinHjjTeW97RRUCfjQ3T//fe7yZMny0KwxhprOCoycHwY7777rrvjjjvcW2+9JdfAAO7Zs6cM5iD33XefOF+uueaa7rXXXnPXXHON/N6FF17YSnpOc86kkKV50qRJ4jzJwoZkTlLKsoDw9dhjj7mxY8fK/ykIf++994ogtuiii8p7tB9ssskm8vfZZ5+V3Z6aASZMmODGjx8v1TNWWGEFt91224kDbpB69AMO8Xfffbd78sknJWv2Ekss4XbffXe5vrgJIc01MG5xtud5wNeC9kSgoT14b4cddgjVNuCoP27cOEkMyZgnOSRjHp+YsLYD+oAM/zwnY8aMkffQctFnJJBlZwiYJ3k/CPfz9ttvS7Z1jk9LkvFSZqLabrnllmvV7mXuf4X5k/PyHIZR1HOU5DqTtGuS578W7Q6PPPKIzFtcN3NCv3793DzzzOMmTpwon3fr1i3RfeVZw9Kiv7X88ss3bHBPmv6NG998hjzx/vvvi0matZV1x08465P0WavU32HPIWC6ZT3hc2QkfO/WXXfdFlknD7kENh6KXr16yb9feuklt+yyy7Z81qdPH3kQ4JZbbpGOUC644AJ3xBFHyHe5CVSLdB62eNS8OCtPnTq15fjzzz9fGu2mm25q9fs4dg4YMMBdccUVba5tmWWWERuzn0kagWnTTTd122+/vXQa5R4w5zDo9WFOe84kIBwcdNBBorpGuFEosYHTok4I9ebhhx92W2yxRcv/eZh40e4swNp+3D+TLKigw8NGMshzzjmn1TlPPvlk6f911lmn5b169MPjjz8uYxIBxQcfBM7Fg8WD7guXaa8BQZzx/I9//EPa8fDDDxehRsHPAeGGxcnnxBNPdCNHjpSNjM8xxxwjv+H3SbAPRo0aJcf5v8GLvtx6662lXZnIgiVwEF4575tvvtnSh2mpNF7KTlTbMW8xITdC/wNzJ3MoQjdBMz5FPkdJr7NSu1Z6/mvV7u+8847bddddZQPnw5zAwsxGh3lLBbe4+0LIyLKGZaWRLVJp+zdqfCNQMYaQQ4IcffTR7qyzzpJ11yfNsxbX3wiGwecQ2CTvsccebcYU9OjRw918882hm+ek5BLYoup5MZhUWAtCGSwiW9hpEOUCulug9AQdQGOz2Mw999zuzDPPlOO5UR4wlZqRjHmg0PCwOCAAosljMjjppJPcK6+8IufCmVy1WPo7NDA7LgbHhhtu2CIhZzlnJRhomIroSM617777ivnwrrvuctddd53bfPPNpb2Q2utNly5dRDvGJEZfIGByreyCIcxHQ99DPUx0IG1GezJhnnLKKXJvnI/7151grfvhoYceknZm7PF7PFBcC1FTjK9tttmmzX1luQadRNlZs2PnYWcczzXXXDKGmUBGjx7tBg8e3GI6ZPLgfDz4Rx55pGx6mKCYzNihURXBn0SCfUDUFxPZtttuK5OZLghM5J07d5Zd5AcffNBGYGPi4TM0jFFamUpUGi9lJ6rtaNtG6X//veDiXeRzlOY649rVv96w579W7c7GDWGMRX+jjTaSCHesQPfcc4/MW9yLBiElGS/8NqRZw/LQSD63PnnWbX98I+AzXjANc74DDjhANgNYsAgMeOKJJ2Sckr1ghhlmkO+kfdbi+pv1W/+toI1jHKOgwXrWv39/mXe510GDBrnbb79dxuJhhx2Wuf1yCWwMxjBOPfVU+UvtOXbwPkitPCTsqnDYA33geEDYzfgOlDQygg1qbhYeHezDhg2ThqCB2D2pMMBiQWNhlqEz6Xg9n3Y87/N9Os2XdrOcsxL777+/CCsIDHSYDsKddtpJInvQNh533HGimag3DC5Ck5l0GPxMpj5hk4T2HTtjJi1U/wq7XkwMaHi4d9TO/nlq0Q+Eg/O7CGtM5EOGDGn5DDU1133aaafJ//0JIc/4YhyjffIFlzPOOEN2cExMtAcLB8ehgSR/HSp9zDB6HSwmaGDRQMT1AULTt99+K/9G8GLXpzAhqsDmQ/+yeGGS4j6zUmm8lJ24tjvhhBMaov8hypxf1HOU9jrj2tW/h7Dnn2jjWrQ7QgHr0G677SYLtv4+32WziZCl95jkvrKsYVnBzItgA6TRwYIRB2vQZpttlus3iyLLmAwb37i2cBxzOJtG7T+O0bWVOZ8XAluWZy2uv4PPISldmP8Q1vhLkEKHDh1avss6g7IGU2zdBLYwDRt+a2gu0CrRCL7AhhpxxIgR0rgIKYrePA9rcOLgRlVCVjMLjYKgg8/Mrbfe2saG37FjRxkA7La4nuCDzUPKDsgn6znjYGDyMDF4MH0Gd7FMVPwm58TuHfSx4AEnp09UMWsmInaDSWBQR2lEfcgtA2Gq9uAgZcJTYQCVvy+sAdeOGph75OEKnqcW/cDOluvkYfOFNYWHWwU2va+844txHNQy0bfqv6LjGA0Dky+CUxB+A98OfeiVuAU72Gf6O5h7fXj2MEvwLOJfkYe48ZKGeox1CGu7Ruv/MA1Ekc9RluuMM9lFPf+1aneUBvi3de3a1V155ZVt/Mq23HLLFoEtKARH3VfaNSwPCDOkmgA0SZU49thjQ9+v9TOXt3/9Nqcdb7jhBrfyyiu3MTFi7mQ9RTDWdCdZxjBU6m8dHwjObI5RQiGcB6+JtZHPwvy501C4ho3dBIOJgYuU6YNaml0OD6raqGlYvXmcPYMg4RLAgLpazTqYc8jwzIOFUBQG5jmgM4Br0mODQkLWc1YC1Sygbg8bzNwPg0QzVqt9nt9B0MGPAidc1Lq1IkrVru2H0EkwAehgxqQRpV3RYBOdFGvZD4ytyy+/XP7t+yL46BjmAePhz3oN/JYKL2HjmMkqOI75bXxf+C3alO+hhid8nOvBGdYnrA+gksDma9gQnEnBgeaziALUcaYZtJvsWn3f1iD1HOsQ1naN1P9sgvGZQiDw3SqKfI7SXidEjcm4579W7c7mUn8/LAhAN9ZsZlA6VLqvLGtYHnyNU9BnOAz6yadez1yW/o0a3/hMB6Nj0fQjzF588cXyf39OyjKGIay/w55D5lQIWosUjtMgsDzkEtiQzmlI1I6AxI5jJxdH8kxfYOMmyQYc1K4h2TKx43AalhKAhzGYMO/BBx+Uv9iR1ZYchT4gqJCRsFk8wiLispyzEqhtIUqYYfAwINmB+VmS0cqhttUIkyiwrfMqkqgFWNsP9S5qZf9YzAtR0U/4bICav2vZD+yq0K4xUaI6D0ODEFB/a9mWLNeAJrnSOAZ/HHNdmGNwjOXZGTp0qLzY8eL/ws4YtwIlrA8gyiQWJrDhp4F5AA1CERHKcQIbztuYPeKCGuo51iGs7Rqp/xHAMcegjfCj64p8jtJeJ0SNybjnvxbtzm/ja4TmRX1Xg+icEKYdDLuvLGtYHvSZ22CDDTKds17PXJb+jRrfBE2hAcTVRqPdtbqEWqr8PsoyhiGsv4PPIUEvZMtA+aJuP9Uidx42JFc1ueBQh4Q8cODANscxSFBzEqnnN4w2SNCcFvzcH5h0Io3D71VC/QV0kEct3FnOGQeLJMIKi2KUhkEjSZDufakcJ3kcKvOaq7Kg4dPBXVmcKS4uykx9LVRgq2U/ELkMcfnhNC1N3vFVaRxHOYbjy8mkyG4XswKTGosQJnQmI65Pd/lhfUAkGlprAgyC4yUosOEnyfkxDxNRVwRR4wVok0pO0fUc61Ft10j9HyUYFT2fpbnOuDEZ9/zXot011RRzQtQmU+esYF9F3VeWNSwPec9Xr2cuT//645s+xD+aeQ2rFJ/tt99+MgdhJSEAAV+x4DORZgxDVH8Hn0NdZzjO30hXg9wCG6Y+BDbUvhdddJEsEkGNErsLnA3prKA9vVK0S7DDPvroI9nNICjSMUmJS+KY9ZxxkEYC0JxFTQzY4MHPz0L7MUiASY2dUBS0TdJgBUyCfp68MFDba/h00K8h2E++KSIqWSqqbFTU3BORQP55atEPWhM0LJcVcA/4HkBR4yvpOPbBl4Pdvu748eFgcqEv+LeaWdIs2OALbGykSHfALjXJhJmEqPHCb6HBYGfM2Oe4sB11Pce6nhP8tmu0/g97nqoxn6W5zrh7jXr+a9XumoIhas4i+hC/trBzRt1Xnr5PCy4GtBVkEdjq9cwVtW6jHUOziFYLDT7m3KClgDUHWSMsoXDSMQxJ+xuzOyCwhYFFQ68pbGObhkI0bIAtnJBdNXv6YBZBDU0KAXxnfCoN5mDCPJwG+T+LMWrJ4CBhEd57771lkaBDVfsT91BlPWccTz31lPxlkCLMBgUgdnH49PG7RPEoCDlEsGBOJZImDkKYae8kYAqrtIjFtVHwMyY++hvCivHSZvgx8pf0LarOrmU/aJvrBBUE51DdHen1VGN86ef+OCYKkTBx+j6YKwgBngebXaC/40sTcABsprgfJjcitzEbUKBdtZ15ibpnJlB8PPBt5LmP+r16jnUIa7tG7X//vSKfoyzXmSTgINhOtWp3zgMs0GHg84pmhe8QlOATdV9p17A86G/R3lEb0Tjq9cxl7d9g2yJMs94gqIUJfqRloW8R1tTFJcsY9n+7UsAB6WPAz7vnwzpDLdIdd9yxRUmTlUI0bMCFEAHRt2/fNsdoiGtQu8ZOnEGBForJPQgLLY3AhK+LLypQTIwstESwYIdW8JNj4JATjIdDO52dPupYBk3Y4pHlnJXw/XZYLP30CeR+wSSF/xoDCP8pBbUsg5domUpZyBGAiXJMQjChZhhRk5+2H+cITpTAA4YDp0bZcDwDlB0L7U2eLv88teoHHVP0BTtJ3wxDJDP52MAff1muodI4Vk2UP455D6GXiTM4iZCagNQATDh+2HiwD4CdG0Tt3NAk8D3SeDBRM3mFQR4izAMckzQ9R9xiSXsQDUZbRmWYr+dYh7C2a6T+xweWc7Bp9s2aRT5Haa8zql39ewh7/mvV7uq4TrJVovp8dwl8ovgd8L8Td19Z1jDI8rxB3nJf9XrmsvRv2PhW96uwaEtyv3LNoAFkkGUMQ1h/hz2HjCmUVLQt/epXPkAxo2k8gr+dhcI0bAgfRJ2FlcngMxbHoK8EA50Bz+AJi6yIknDPPvtsSXaIEMQxlB4hdw6LMA6IqCavv/76luMJ4eYaGAxR5sm054yDe+I3AedJBiiaBgQGhDUCM+h4Ev4RVevDAxmWsTwMNBlFlraKWoD99tPFV/uGXQMJU/kOueZ4oBDUUN0T6YMpTAW5WvcDwS/soLge/qL65pp4QPEfZFzxl520P/7SXkOlcRw2ydL3+E7gT0EeIH5Po494j3/zGzrJh/UBaJ4gBDEWH/JO+aHrmECYYHDSVSfbMNCG8hsI10UIbOq/Flf0u55jHaLarlH6H5cEjgtr/6Keo7TXGdeulZ7/WrQ7cwLzFJoYTW7K4o8Ah2KB5wVBCrNbkLD7IvIvyxqW5Xnzz4fVSnOJxUHUIslplXo+c2n7N2x8E9gBuHUQZICrDUI5OUDxSdM2Yc7H6odvW5YxDGH9zVwafA75TQROUkihiGGdQdbB145kyYwPEudyv3kpTGDjgfRNe61+5P8W7LC0CknU2WGfo8pFEECF+sADD8gLcPhDVUr5CV9dnGRXkvaccTCR4AuBihVfNoRVJghewMOCaYqBEHwgkjhqVwPs7Axg7lcfCiXKd4ZdJZE39C+TnQqp/B9BjpBzfydU634AVOg8QAhp5F8C2p9IZYRpBLaixleacUxqG4R3csAxRtTnEdjRkTOOSOtKv0HKGMYbu0uCXDS8XFE/NkwEqlEMortGiHKcDhI3XvR6mSjjqNdYV6LarlH6P+55Kuo5SnudENWulZ7/WrQ7MGdhCcIxXdcl1jFcVPhNBDaEuiBh95XlGrI8b4BgoVofTQpbiaAms57PXBHrNnMY5kt86zQ9C3CfBA7gT8YxJErGLQmBLcsYhjT9zWYYzSWCpPpAAgoChGbV3OYlt8BGqQdeYaBJCtZv86FBeEVBA2tS0yBIsqibUXXygHXq1ClUjQ00VpIGS3POONR/jV0XteWQ4tE84UOEkIMJVBMpBmFAsPuqNewO/fp7PmHtpxMHMNEx8aH+RRhiFxumsq51PwATADsvzsULfwMmAG3/sLxJaa8h6zjGtw/BnckbvwwWDSKGGTNBotqOHTrmaK02EOSFF16Qv+xuo7SaaMXZYPD9qOjdIHHjBW0ewntU7julXmNdiWu7Ruh/2i6u/Yp6jtJcJ0S1a5LnvxbtztzE5pnzoyHDrxqtEwuuWonC/LvC7ivLNWR53oDnV/2Gs1LvZy5N/4aNb5QBCGasNWiwWG/QZuH6oRovAgoYp342irRjGML6O2oMI3SiYSO3H3MufnpoDBlXRWopcwts9QQbPPbjIutwFnHOsDBvBkbc4ACcw7G3N1p9OGBghuVVy0qRfcuDnOX6qjG+gqCZTlrmLAomrTATBxpFQvjxQ6m0MLCLRJgN05alhUWQ3T+TKOYAJiz8eNjJ9uzZ03Xr1q00Yz2q7aBR+j+Oou4h7XXGtWslqtXuavbENMVizILuL+r4UDFOGaNhrj2Q5758inzeklKWZ66I/sVfMMxnEGhXDQTwyfKspe1vBMFKwRx5aGiBrayohi2NuhvY/TBRlKEQvNHY4DOpkVuUoIoDDSnHkJanCNjx4g6AJhmTM88BQR8Ep5CkEmysG7UGzQpjHEdz8nFpFCFgHiXtDZp3AnSqSdHPW1LsmWt8TGArGNSnmjDXj1RJAupiylQZRlb22WcfqS+IyQE/M8qjBcPVg7BwjRkzJjI3VVoQEjF74LSrtfy222470WporUcb60atwdkcE5yaQdGEYGbk/7h4ENWM83mRloIwin7ekmLPXONjAlvBoFLH4b4WWY8NIwjRUmwY0HIRnZwkAq0aJZ8wQ6uwBmjX2MD4JdgMo5ZgJsNFgPRSRFliHmVjjVmUlAv4OYXVxy6aajxvRvvABLaCIddM3uR4hpEVckuRv8gXlsrAZpttFllg2TBqBcIZaYiAiEKc3cPScRhGGTGBzTCaCBafsglrYMKaUTbCHNMNo8yYwGYYhmEYhlFyTGAzDMMwDMMoOe1KYCMPDckRSZwYVzIn6Xnmm2++Aq/OAMqMkNE7bx+lhXIjFCYmR5CZSto3JP6ltBpjMCofF/nlvv76awksKqMJ2ifJ/RiGUX7ajcBGVnayFZMEj4U5K0zS888/vwhr5PUxioOSLfQRYe/UiUsKNeeoFQfDhw/PFIlIuZMtt9zSbb/99u6mm25K/X2j8UFoJxv6JZdcIgIZpWj23HPP0PHF/ymnQ5b7c889t85XHk7U/bQ3ipgf2hvWZuWk3Qhs5NkhL1WlgtSVIPkg2rW4ephlAU1V7969JdcQ+bhqqbGKI+q6nnvuudAC55W47bbbJG0EQnTWxVOrU9Q7C7hRPyiDwzgiJQq1BbUWatj4aoTxEnU/ZaCWc1MR80MZsDYz2o3AVqlIb9rzNILARkJIcg1R4LYswhpEXVfWPsKMSj269dZbL/M1FTU+jMaE2o5ooIiypSi1n9Q0bHyVfbzE3U8ZqOXcVMT8UAaszYx2I7AVtSNuhJ21UlbhMuq6tG3TXi81APOAxhQTAIsbk6HR/qBYPYW1119//TbCTXB84V7x8ssvSw6vpZZaqoZXmZy4+ykDtZyb8s4PZcHazChEYGMHh/PtOuusI1nW+T+1DPFF2mWXXdwKK6wgx1EF4MEHH5SFmfI1lKtZccUVI8/LpEgJD8rckIGaxZRahKiEw8C59u6775b6hSRFpPzI7rvvLs62QUEL8yhZ4XEyDyvWiq8aD4j+rsJ77G4w2+U5D+AITA07kp0yuZKraueddxY/rjx8+umn0v60HSCI3HvvvVJDLu+5q3ldOiHRtvgZ0q4cT9tQj5K2Cev7++67T/5usskmrd5HEKPf+fzDDz8U30OKoG+88catjnvzzTelnyjEHPTVIAktpZ6Accw5uC6ctykijR8jRaVZIH/44Qd5j+oCUTvgd999191xxx3urbfekmdgpZVWkmLTjJ8w0o6Rao0pH54z6jFyL/iEUlC5UvmrsoLwRf+R+R4oT8SYRBBbdNFF5b3g+Hr22WfluVfT/YQJE8QHkv5njDCvMecE4TwUoKY8F6XDrrnmGhnnF154YavxknaMZLmfJNfB80gNWOZfXBUQ/Lg3TKxhJHne4uYAzG9Z5tJK9xM2P+R5hincTp9zL6wx/fr1c/PMM4+bOHGifN6tW7dK3dRCkue10rxZjf4sus2MYsgtsDEw8I3YdNNNxWmbArq//PJLy+fYvxGgGEj77ruv1BdUTj31VBmsQd8K1LHURLz99tvb/B6D8tZbb3UdO3Zs9f7jjz/u+vTp495+++1W72OHxx7PBMIA1YkUYRC/DnYrWqzdh9/eY4893AEHHNAyOTCRcm3UmmOhynoeOPHEE93IkSPb1HY75phj5Hq32GKLNudKyqhRo+Q8Cn3Ai4mmngJb3HUxSdO+Cy64oPiy4RyNgK+cf/75MmEFAwKmTJkiY2/ppZeWMaZgPqDdGXtBevTo4W6++eaWDOdRmj0WTDYIr7zyioxrxikRwixA1OWjj3ifRdK/JxZLJk0fgigGDBjgrrjiijbXs8wyy0ifcw8+acdINceUwoRPTVDa3adXr16yQKB1aiQQPP12QVDixThDwAkbXzpeEKQOPvhgd84557Q658knn+xuueUW2cAqeh6CWlik2chitmSToItcljGS9X7irgMBgc9ZkIMcffTR7qyzzpJSTj5Jn7e4OYA6zGnn0kr3E9Z/WZ9hlBGM/eA9ssYgQDE/0OcquFUi6fMa12YIXkX3Z5FtZhRLboENUxIwUbz00ksyuFDDs9gxeBCUeAgZlAxQFkAilhCu+C6DxRfYEIiwmzNQmBAPO+wwKSfChECtNx6W/fbbTyYhhfpwm2++uQiKSPk81OwE7rzzTnfmmWe6bbbZRo7zzZiVfFD0vsK+4y/sWc7DQ3rSSSfJA3HkkUdKOSuEFSZqdjaHHHJIrsV1q622EqGSmnUIlirk1NuMG3dd7N6ASZvJhYmEscJumj48/fTTZdLXOplKWPuzG2WHjpaVsdS/f3+38MILi2Zk0KBBMvEz7hhbUeegH3baaSeJXGUSYqIGXay5XnbZTKRcJ6lAuEbOO3r0aDd48OAWUxQ7Z8Y4v8+iecQRR4hmmYmRcYBAyD0TGENtQ0g7Rqo9poC212cZAY2FGCGDyZoFhv6lzRqJLl26iHaM/mXsUbYIoVOL1IeNDX0PsxFzGf2JJoIFjPqtjBHOx5ylaTT0O8xrzFEIYIxR1WBkGSN57ifqOljs+feLL74o14NwxCZv0qRJ4uiOtpnxRYTsDDPMIN9J87zFzQG62GeZk6PuJ6z/sjzDKAIQxhB+KCJPdDAawXvuuUf6nGdLg9qSkOZ5jWuzu+66q/D+LKrNjOLJLbBp5zKQ2BWhIQEGxd577y1CFpM6Ap0v6DBImIB8bRygXmbwMch40DGrAoOna9euYnJAEGM3wW+gJkeFzHkYREOGDGk5F+p4dhmnnXaa/N///Ur+UnGDNuy9pOfhoWYHjgkZbQWqdP0+EwKmJe4tD0zaqsnEbMNuqQzEXZe2I+3DDhUzm8Lkdt1114ka/oMPPogV2BCwmLhYPPiLk26HDh1afpPxgKYXza4KbME+ZAIaOHCgmHSYPBl3wd/jOhnTuhDCGWecIYILiyxmB524hg0bJosXEym7UF3E+S4LHOYqJlQWY+477RipxZgC2hJhjbqg9IeCcMDGjI1Vo4FggRkc4Yb5hDHjEzcPMJZYwDDXK2ghMJPR/8xfzE3+eehnxgPzn1/DMu0YyXs/UdeBSwmfMXci+Oln3D/CODnnmGt5scCnfd6SzAFp5uRK9xP3naTPMMexViGs7bbbbiJU6W/wXQR1NpVx1+6T9nmNa7Oi+7OoNjOqQ2ECG9ozFdYU/H8A81ZwIOtnfo1BJHcmKxZKNGjBJI/sQtiRsNtEm8eExOLKg8Qg9oU1hUGpAlslbZnC4GWQI4T6Jog4DVvS8yCMYvPH5yAIZl40kzrh5SGJAz8CEAJxlBmLh5DdYxKYDP7yl79kvi5tR1IRBBckJn2dTNQPJ/g97VtyTuEPQoQTQkWwsDOLK5+paZwdKBoCFjnOjfDBosOExP0zFqOu05+09DrVx06vk4XsggsuEF8iTPnBMU2fcx7G/uuvvy73nnaM1GpMqemG9vPhnooS1uoxJlVzE/asBMcXcw2bBsBM7wtrwLWjeaTPefaD52HBR3vsk2WM5L2fsOsAxu0NN9zgVl555TbPDv2PnxobJk0WnPZ5g0pzQJY5Oep+4oSPpM8wViN8tdi4XXnllW38aHEFUoEtiYYty/Naqc2K6k//nHnazKgOhQhsdFhwJwf4IsGOO+4Y+Zk/KHj4gZ1YVEZuHeQMEAbb5ZdfLv/3bfw+mNSAwcqgBY3yQp3LbjgIDyeO1exs1Q8AXwGuGcEBZ8+s5+F68NdCYEVbiEYRlTc+GVxjUUWy4wQ2zDgsKvhd4HeEOrxWhF0X/agTAu0RhN3le++9JyYINAgKeYnQSmAi0sAWUhlAcKepcBymKgXTAO3RuXNnt8EGG4gGA+izoLCm0aRR18nCG7xOzIX0NZM61xoGvw/ql5l2jNRqTGGSwe8UUyDmOvxZiqoKUc8xGeXWEDa+dPxiegqb80AroOgipueBsEU1yxjJcz9R1wG4ofDyQVvHc3HxxRe3OW/a5w3C5oAsc2ml+wnrvyzPMIK5/kZY0JOaqJkvkgTfZHlew9qsGv1ZVJsZ1SGXwEYn4XPGjie4k9VOZqfgm5SUsElFHU3xfYuC3QfwcLBTYcfLQEHlG4YGIaBWVvOqRnlF7YbCro3dHep/drcarZXlPFwrKnWcPNEmDB06VF5oFPAJOPbYYwvRVsSlH8EhGlW8RnJFwQLNq0jCros+1SjNMHU64ygsWTGaVnaqmAkwL+AYy6TPmFNTVCW0j4gURcuGppgXu2rMFr6/kB9NGnWd4F8nUdGAr4n6m0Shk13aMVKrMcWCwsKCSwI+qIAJpIhJup5jMkrACY4v/1hMZFHR6vj6gWoi9TxYCPBFCpJljOS5n6jrAIQitJiYc3kumT+16ogKSnreLM8bhM0BWebSSvcT1n9pn2G+jwYeDZT6QgfRNSZpuo0sz2tYmxXdn/4587SZUT1yCWxxDvcIUzjSIt0HtWXsFtUMxU4VUM9+9NFHEsYetYtkgiAqFS0bA5SBCHG5kJhQIE2ggKZxqOS/luU8gEDKooM2AbMNEzYPBaVAeLC45jxpEoiuZCFFaxS2+BGkgY9g3MJYDaKuS9s2aF4Kfh5lDtD2xUwOnF8nm0roufkOggi7SszxaN4wT+Fcn/Q6w0w6CPosaDjlVsL3zUs7Rqo9phCk0ADRLvjcEFiEC0RRO+p6jUlQK0Ew7U6c/1pctCaLHqjApueJ2lRmHSNRVLqfqOvA3IoPHiZfTI/cNwFenAfrBA7r+KLled6i5oAsc2ml+4nrv6TPMG0CrDFRArr2dxqBJc3zWqnNiupP/5x52syoHlUT2OI+Q1jDd4gOVjU60j9alLgFAFMJEBHK97QmaFSqCs6nZtak/muo5nHUTPKdLOdREGLZsemuDf8UHmI0lvw7TPWclDjtGj4GPPzAg45WI+48fjRuHJikEbazXFelyTrp91DNAxNbGOzgMQWwOOpipufAeVxNMZjjmMwuuuiiVgJb2utkA8LOFBMI50tL2jFSzTGFRglhDTMg2seo2oIsXgi9mqIF2Gh16tRJduJheRfrOSbVSsAGMOg3F+xv3zQU5ViN2wRjjHvSe42bJ/KOkSz3E3YdaHpwCaCvSFPBMxCMRtVnR01sWZ63Ss9y3jk57JxpNtnB69O0FlH9zTqGX1vcOaNI+rxmabMs/emfM0+bGdWjEIEtbMDE+VCFDQAmQ2Cg8e9gAj4GseY7IvcR6ISkk30QnGB1Fxg2ADGTBsGfRAvF+4JgnIYt6XlOOOEECcnef//92+QxYifEpMZuK28S0ri2Z0FBQ8IEGJac0ocFmsK/SSAMPanAFlXhIM4c4icr9t/3v6f+VH7+Nh/GA7X48KnEEZcFh10tGl3fbwbzDnmGyHOEAKJa4EoTV/A60QTzfzYWmBmC7cM4J5KaRZZJFa1N2jFSizHF84W7AhoGhNi4QtCa2NQPQKJ/cSMIe06gnmMyzaZTrQbAPBWE/sQpm79Ex6vrRNxvZBkjRd2PD0IH96SblSCkr2AOZnFX15K0zxtU0panmZOTPI/Bz9M+w7ouce9h4EPN/fOdMNefIFme16QWBp8s/Rl1zrRtZlSPzAIbu6egc6JP2omDHSFqdXab7ODJpaYQLoy5hAWWiFONUtGFlAHNrtxXDWPe0nP4pld2RCrgMQn6Gj0GMRMt+A8HzqFM1ixEapLIch6O4zwsTMGHlVBp0lnw8ATzgSFUsKBFOTkHUcf5sDJLqNqZhGjDSpnTqRKRNK+WJhJOe12Yx1mE/T7yoY2ZEDEv+RoD/AmDUWMEg6B55R5pNz9LN4KXpvHQto/yvcBfhQzg5IVCQGGjUOk6VbPhXyfXhn8JmwYiG/FTUXDuRaDAgZ+JTu8h7RipxZjCD0bRBUzhueN59lOkhC0smGCiIlXrOSaj5qmw8aXHAsIT/nx6TxyPcIJmhDGgefv0PAhmwehavca0YyTP/URdByZvCKvQwMaFdgcN3IK0zxuEzQFZ5tJK9xPWf1meYQ0wI+ks0bC++w0uOfQPBOenKLI8r2FtVo3+LKrNFJ1n8NljPjXyk1lg4yHF74yHKKhqJQT7hRdeaPE1CxI2qXAOnC2PO+442RXQ2ey2ENZImEqkIPmfmCgVBEV2JUyS/EWdjLaEQU+CXa6Nv+x81PSKUMggRlWMJoUHjgeEh4WdD6pvBqF/bSzsTJ7+e1nOQ+JCfBTwWyDfDgkYNSqH9/j39ddf32rgs2MnQooFIKnApjl72M0xwZAnR6NraXu/UkMc9Elcks60hF0XEWRMCizWYVFmUbtL2oTIXc31BAgg9AOpXohgZDwgYOPLwRjid0jkSRkV/9xhmwo2Bghs9BcaHRbUuOuM0jafffbZ0s/kSOL3+G20BWwocAPAnESfK2nHSC3GFNpH2oh7JHEuVUgQsNAEsGjR/pTjYUHhGMooBfswzlxSzzEZJeCEjS8dL2iMSEjLd3DPYHFkDiJ3FvMPgQMqyPnnifKBSjtG8t5P2HXgUA740eGUjjmXhRhXAfyrNFcY94lrCr5QaZ83iJqb0s6lle4nrP80IjzNM8waQx8jOGpSYK4VAY70P5i+EUowPyYhy/Ma1mYIVkX3Z1Ftpug8w0bGBLZiyCywxWnQ6GR25QzI4GDCpMADzYAJ+j7QwQwOUgfwoGpGZxwt2WVhCg0OGlS/TBQIaWjmgIkfwY+dGgJb8BoJ02aHgf8IGcWBiZbfY4Cx003iK5H2POTKwbeHvHCU0uKlsNiRR44FUdEdD0Q5fIZBFm76gJ0UEWsaeg+VFs9qEnZdWcwace+joUCYYKJS3xKgX0g9oDti/xxhk40mK2VXzQRKX2S5Tkx8LOCYtaixywsQ+NmYEJHqm3nSjpFajSkcodEIIKCpZpJJncWYNue3ODcbtREjRrR8j3mAtonzn6vXmFQrAX2hC5wSZRpC00CEHwIZCzbPOfB/BDm0sb5WI4lDdtoxkud+oq4DawQCOP6BmsYC0JzQ91g3OIYNNOZxFnhI87xB1NxU1Jwc/DytaS/sc/q7b9++4qCv6aOwtpDZn75CYEOoS0La5xXi5s0i+7PINvPnGQtGKI7MAhsaCF5hsBAETScKwhS7iNCL+b9Jj1QKhx56qHQ2+WKw5Ycl/VOYyNgxoGbmhV8FA0QTrYYtFEj7TJKomllQUHurGh7nana6PgiSvPKeBxA89f7wMeDBJ+9OMOkw4JSKuYB7jIoECgPNCeYazXbuwwMWdi+1IOy6mIx4RcHEpomPfVgIgosBsFix4ycvEcIDfkFsDNDgBDUzWiA7Co0QU7JcJ6B9wOTD+GRyxwE/zoSSZoykPT7rmOJ4ombpO1IDsLFCoNWcY6A7dN/MwuKAhqCShq0eY5I5xa+H6BM2vtQ0BSzWLN6Y/pjT0MSEmZ+ixmmQtGOkiPvxYe6lr7gfxj33hLYM7ZZqW3COZ3z5KSfSPG8QNTelnUsr3U/Y51nnGvoVDRv9gkUAjTP3xxqHEoFnqpLvpU/a5zuszarRn0W2GW3iu1IYxZA//XkVIOM3Go6kMAB5gKJy0YSBYOf7XGQly3kwAVTKVq6wq+I3gjvmSvCABk1MmByCpoVaE3Zd1YBJMM0kWm3wzWIRUp+YSqQZI2mPzzqmgHbVZNRB0BwAGjO0BGgP0MqRo1F9P/FHRIuA2RQzahnGZFbSzjmVSDtGqgF+SmG+SsCYiUqUnOZ5i5oDipqTi0LNnmiREZoQbHxhFd9CxjNjOSrRexRpn++s82bW/jTKSSkFNuO/sIvHvITjexGgyWBiqeeCYNSXoseUj1aHwNcUzRCLG4KbH2FHkAJ+qCQIBRuTRllB+8Rzgi8dOdP8aErMo0SSY8mh4Llh1AIT2EoME8SYMWMKK6aL2UXrQRrtk6LHlA/uC/jYYNbDdOObSxVMX2grNNLbxqRRVggIwDStZlA0iPhk839Mt1iC8G8tUstqGHGYwFZiii7BYxjVHlNoy4K1C33QruHjFpfLzTDKAOZCKnCQvQB/V8yj+OWhOcbUjy9alHuAYVQDE9gMw6gZmEuLKkZvGNUG4YwULkBkJab+qAA4w6g2JrAZhlEzTFgzGhVz0DfqjQlshmEYhmEYJccENsMwDMMwjJLzvwHRVPXXU+F6AAAAAElFTkSuQmCC"
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The pull-out curves measured for different adhesives used to realize the bond to the matrix were evaluated as the strain in the FRP sheet at the loaded end versus slip displacement. "
]
},
{
"attachments": {
"0e4f48fa-0996-4c4a-be4c-7a2f893ba91d.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAi4AAAFqCAYAAAA9a9E4AAAACXBIWXMAABZIAAAWRwGq8zFRAAEpI0lEQVR4nOzdCbi2V1Uf/NPWznNrZ4dqrdValVqV0YFRJiFAgISEkJCEISFhCIMBkkATIIECgTBDyAQhAwSCzHMtQhUQJ6zaWovVWq2tdrTz932/7fd/3e+d+36Gc84znHPW/7qe6z3vOfdz3/vee+21/nuttdf+iv/n/8NOoVAoFAqFwgHAV2y6AYVCoVAoFAqLoohLoVAoFAqFA4MiLoVCoVAoFA4MirgUCoVCoVA4MCjiUigUCoVC4cCgiEuhUCgUCoUDgyIuhUKhUCgUDgyKuKwA/+f//J+d//E//kf7FAqFQqFw1PCH//Af3vmjf/SP7nzFV3zFzh/4A39gX+9dxGUF+N3f/d2df/Nv/s3Or/3ar226KYVCoVAorB1/4S/8hZ2/8Tf+Rvu3iMsBwK//+q/vvOtd79q56aabNt2UQqFQKBTWjrvf/e47J5988s6d73znnT/yR/7Ivt67iMsK8Mf/+B/f+Zt/82/ufMd3fEfzvHzxi1/c+d//+3/v/K2/9bd2vvVbv3XfB7FQKBQKhU3jv/yX/7LzMz/zMzu//Mu/vPPX/tpf2/nP//k/76ziVKEiLivAV37lV+7c61732vmGb/iGnc997nM7//bf/tud//bf/tvOXe96153TTz9950/+yT+56SYWCoVCobCvYOuuv/76nd/+7d9e6XOKuKwAf+yP/bH2kZgkz8XPEnYRmr/9t//2zp/+0396000sFAqFQmFfYVEup0Vi7ipRxKVQKBQKhcKBQRGXQqFQKBQKBwZrJy4Sdf7v//2/O7/yK7+y81u/9VvHap38mT/zZ1oo5S/+xb/YklfnbZ9yD3E097H92P+FZP7cn/tzO3/lr/yVnT/xJ/7Ezh/6Q39o9Hu/8Ru/0Z4NX/d1X9eSaXOt9v3P//k/W6zO53/9r//Vfi/s8+f//J9v1//BP/gH9317V6FQKBQKhfnYCHFBVq6++uqd2267bedf/+t/3X5/l7vcZedhD3vYzgknnLDzl//yX25Fa2YBufjsZz+7c+mll+78y3/5L3f++3//7ztf8zVfs3Of+9xn57TTTtv5xm/8xtFcErkm73vf+9p2ZWTlRS96UUui/VN/6k8du+bf//t/v3PdddftvPWtb935D//hP7Q2y5C+3/3ut3P55Zc3UlTEpVAoFAqF9WOtxAVpkKx61VVX7Xz4wx9u3hIeDSTAlmEeE4k9D37wg48jEj2QCN+55ZZbdm688cadn//5nz/mtUGCPvCBDzSS4V7f8i3fctyzf/VXf3Xnox/9aMt6/rmf+7nmPfnFX/zFna/6qq9qz3Nv133mM5/Z+fznP7/zn/7Tf9r563/9r+/8zu/8TvPQfPrTn9655pprdh760IfufPVXf3WRl0KhUCgU1oy1EhfEAAn4yEc+svPlL3+57bCxRRhZ+MQnPtH2f3/yk5/c+e7v/u4WLhqrd+IethYjOl/4whea1+TEE09sYSbEBbn4kR/5keZx+fqv//oWBoKf+qmfamTpQx/6UPvZ/nIEBzlRYwV4bYSHXOeaP/tn/+zOSSed1AiPbc32pr/jHe/Y+a7v+q5Gdoq4FAqFQqGwXqyVuMgvEeJRlA0BQVAuuOCCRiKQg0996lONIKg8i4iMERckg6cG8fE9XpOzzjpr55u+6Zt2fvRHf7R5YBCgf/7P//nOPe5xj2PERVjp5ptvbh4fYSg5K0MgLu794z/+460NSJXKf8iMtvPSuI/cmlUU1SkUCoVCoTAbG9tVhDhIxHWWgRwVJEUI6Dd/8zdbXgmCMwbkgkeE9wMBkcfiHhJyk9yLfMhT+a//9b8e+577SuL9/u///lbdD8GZBYm4cmaErlTB5d3xrFUX1ikUCoVCoTCNjW6HFmpBWBCEb/7mb975yZ/8yUnCEmRXkn/7UI2f88l1Pe52t7vt/NW/+ld3vvM7v7PlwSAys05vlvOCDNntpJhOhYUKhUKhUNg8Nl7HxdZiJME2ZlX35hGX3eLbvu3bWt6LvBahIIRpFnFBViT4+lcb50Fo6Zd+6Zd2/t2/+3fHSBOPz5e+9KXmQRoLTRUKhUKhUFgOGycuyXuRcDuLSOwVCAt41iLeE9cJKWnTIqQDYRFOklsj2Rh8Vz6PBOC/9Jf+0t5eoFAoFAqFwuaJi2TbeCsUhtuWc3yEkpAQbRJimge1ZyQbOwEaGYN4XOTjFAqFQqFQ2Ds2RlwQFh4NngrJuQiC5Fw5JX3VW54PfxeykTDrb4rV/eN//I9bDRbJuv/xP/7H5tVwPx87iYSdxnYlzYJn+p7QFa8J8uLZvCb+1WYEhQdm6LXRNqGlVNoF7fJ/91ulN6lQKBQKhaOCtRIXuSKIh/ot/+Jf/ItWK+Xaa69t9VcQA3VTFI0T1kE+kBFej1tvvbXljdz5znfe+cEf/MGdv/N3/s7O3/27f7d5MxCfd77zne07rkU2eD1sk0aClgFCouCc+9tujbAodIcA/cRP/ERr0z3vec+2c2lIXHx3GFJCtrTB7qciLoVCoVAo7B1rJS48GjwT973vfVsNFkXkfuEXfqGFVBj3O93pTu1virvxXiAlP/3TP92IC6Lgmoc85CFt27MicLY0f/zjH2/kB2lIiOb7vu/7dr71W791NOzkPjnTKOcP5XgB/0eAfJ8HSM0WBedc7xq1Yh75yEe2a2qXUaFQKBQK68faQ0Xqopx66qnNo6GwG4LAm6LY28Mf/vBWqTbl/pEFHgvl9ZGGu9/97scOOPye7/meVqsFsUmYybbq+9///u2sIl6XMfiuui/CTTwp3/u939s8PT2cmQTCTv/kn/yTRrI8z30f8IAHNCJTKBQKhUJh/VgrcUEahE8Qhyc96UmNZKRIHC9LDjuMN4M3BKHhHUF4+jL7wjUOPVRrBbGQk4KAKPOP6HjOGBCf7/iO72jX+dl3hqdIy3NRqE7YSDE7cE8hJKSlvC2FQqFQKGwGa/e4JM9FWEieSpJZ5Y/wgPQkAkmwowdp4X3pT4wW1lHRFnGRNCtMhKy4j+umyIXn25o8tT3Z97QBuXLNP/gH/6B5hLTFvfsid4VCoVAoFNaLje0qQgQWCbkgGlPXpeT/KhCihGQVCoVCoVDYDmy8jkuhUCgUCoXCoijiUigUCoVC4cCgiEuhUCgUChuA3EwbS3zkaA43ihTGUcRlBVDt124pBexs2V7VwZGFQqFQOJhAWhzAqwCrs/psCFGZPTtXN70JxKaUHBi8De3pUcRlBfit3/qtVrzuE5/4RBNK9Wps3y4UCoVCARxX88lPfnLn5S9/ebMTZ5xxRqtlpmbZNpTdQKyyY3e443fTKOKyAuRcJQyacC57ZlKhUCgUDid4VxROVdzU4vbnfu7ndn73d3935+abb26V5BVFPfHEE1s5jr4EyDqBsGjjj/3Yj7XIwb3uda+dv/f3/t5kGZF1o4jLCqCAnQJ33GxIzD/9p/90000qFAqFwj5APoqz5xh0i9Kpg3en4PDdd73rXe2gYOfrKaAKzu/jrZde4Mw+XhcL4HWCzeJh+dmf/dmd973vfTsf+chH2tE73tVROIqwCm85b9DRN2zdJlDEZQVQ+0VxPBV/CaVqwKkQXCgUCoXNgoHmVfABng2hEHXDZgFpcfjvL/7iL7Z0AHXEnJv3jd/4jY3EzPs+8K5YzDprL6Ql8H8HDqvY7p7rJi7yMZGn9773vTu33XZbOwgZfv3Xf721S9FYBOuBD3xgqy4vrOW91x3WKuJSKBQKhSMHngPeDeRFhXYLzXlhfaTjZ37mZ3Ze+MIX7vyzf/bPWjV1oZ2LL764eSAWKaqK7DzoQQ/a+e3f/u2dL33pS8f9TRuQAx4XP68bvCsIi4ONEavAuX2f+cxndn78x3+89ZeQltzNs88+uy3Si7gUCoVCobAPYIjlGcrNiEdEmIdX4Q1veEPL4xAacSjv6aef3kIhyMgYeFrkpLzjHe/Y+cmf/Mn2f/f7kR/5kZ0rrriiHcL77d/+7XPDJw4OfsQjHtGee/vttzcyAI6vuec973nskOBNHOarTXJwfOKNAh4q3pjskOWBEUryf+cOyudcZ5X5jREXLjdusd/5nd9pbjrnES374jpZxxFOnWygsVTxxjGXnXORMEfPJcSY75SQua/Bw4qBsLl3TqcuFAqFwnaCfRFu+fSnP908A9/6rd/aQjpIyS//8i/vfOADH2ikQY4J8KI4cFcI5Nu+7dtGd/UgOR/+8IfbTiB2IVuF7QhixB3KKy3A92eBfZIjwusC7iPv5S53ucvOgx/84J173OMezS4tEnbab3iu9vtIb/iN3/iN0evYR33HprKjJ598cgttrQtrJy7IBgasQ7y4eBnCwj0moRU5EGucRw6wZqSH0BAoJMOWYy4293HPfuCRFQLseb/6q7/aiAgXV56Z06QJEXKDURLwCLaTqw0mlyIUeSkUCoXtA6PKNnz0ox9t3hE6/Lu/+7vbYpXet5vnla98ZfO65JDfL3/5yzs33HBDIzwIDM/LEMIj7sXTEtICviPsZHfQd3zHd8wlLoHrkBj2hx27//3v3w71RX42BTk197nPfY6F0BA//amf/L9/b7+TtHvLLbfsfM/3fE8jY+vC2okL0mKAr7766sZcERgChbg87GEP2zn11FOb4MzbM26gP/ShD+1ce+21jVnr3K/8yq9srPo5z3nOHVx+kqHe+c53HmPLGLXEIsJy0kknNVdXIOnq3e9+d7sW2QGESPue8pSnbCQZqVAoFArz8Zu/+ZttN4xQELLB5vg/+FliLbtjEd2DHeGFYXsuueSSO+j4H/zBH2xeCDZBfku+z86wD49+9KN37n73uy/VViGhr/7qr27kB4nJAnpT8M7a8JCHPKS1B9GzgLfYR2Y4CAKeFnaW58g7rNMmrpW4GGikASmQ6MM9ltgYIvLDP/zDrbO4nXTYGDA+gywu+MEPfrB5UGxHcw/k5Ud/9Ecby37Uox7V2KtnpiDcxz/+8cYQCZl7eObb3/725uKz1UsclGcGU8fKsWjuL4NF0CUt8eIoEvS1X/u1RV4KhUJhi8Ae0N/XX3/9zi/90i+1ZFo2gw5nc5KiMCQtIGWBB/5Od7rTqG7njbjf/e7XbABS9K/+1b9qi1heFnkeFs2M+aIISdg0WemR9/Yed7vb3Zp95mGyo0iYjA3Vl/rivve9b6s3o74LG7pOrJ24ICs8GUIx3/zN39zYms5CZmQxv//9729uJwI0lpyUJCH7zMUlXXPCCSe0juPGe8973rPzsY99rHlTkA5smIBhyEiTZz7ykY9srFlSlTDTF77whebm4ulBUCReYZmSpdw7CViK8dx4440tFvk1X/M1RVwKhUJhjQjpyMJ2qIOlEPC40Pe8Iwlt+Jdu/7qv+7pmaHlVPv/5zzd7ZLEszUAeTMI1Y0AweEiQFcabXfFd32PEhXi2qbrsXsDm2SXFBuo77ygPFZHx7n5mpxWmYzcP9a6iZCwjGH6+853vvHPuuec2YUQUfBAJAqHDxohLPCiu4bpCUB73uMe1HBReki9+8YstFMUdyGMiJ8U9eVd0MAETGrI/HYt0fbZ2EUpC76OdQk/cgwbLQGLsSA5h72N9hUKhUFgdeEroe3pdboVFKU/70Fvhd8IXPqmTEl2NnMjfQE6Qj1e/+tWN4EhIZYssUnlNvuqrvmqyHZ7H2y5lQNiJXWCnlilAd1CAhIWI6ROpEvpOrov+y3tvAhvbVWTAueZ4RHSAjknBNkI6RQy4/mSEcwMSFB2rE30IlXv6fs5YIOTim8iJ+3tWn7TrOQScB2gK7u2+m8jyLhQKhaMOGybe9KY3tXCFRaVcErmMfW4i8ATYUiyU8YIXvODYxg224TGPeUzztv/9v//3m+1AbqQQSOT1e16cRQzxkKwcNsIyhT4HZ9PvvdE6Ll48ZCCVC+d5MvwdueES7DsuHTnszOwScj0MyUdCT4gO5k2YhZPkwiBHF154YfPqCEul+i3PC6LFfVYoFAqFxZCS8v7td4/m99CXnPA7HnqVXKUTyGFJnorQjBwLOSnR6+6JvAj3nH/++Tuf+9znWrkMnnceFbo9JTB4TuRGsg08NYuWuti00d4U4ijYBhy4AnS9gC+KTJR5wCYJ8A/8wA80Fo6Ny5cRekJaUnxH2Mlk6CF/Rrip3ypncnFtIk5HUdALhUIBorctBulE+vKud71ry6Pg0RbWt7ECqZCHIvRPZ7qWh/2mm25qelh4BoT5nfcTTzjyEtDjyItEWvcR2rfxws+ISnSx5w49NoWDgQNHXHovzaLXc+stcspmBFoRICGp1AMAP2Ob2ec/LFyHtPDEmFCuAUzeFjuT1EQqFAqFowghe+F4my94ThCYZz/72S3nhOdEruGLXvSiRjBs2BDWpzPlFCp7IScxehX8jNQo/EYf98QF2Ag5LT6Fw4cDR1xArG3R476RDVnkSepaBCaMejKSkeLdefOb37xz5ZVXNvZu6/SwyBByZJIgPPmOn3lbtmm7W6FQKKwbNjwgJk5EVuwN8bj88svbTh/6XChIrqFkWYtFoftTTjml7d5U40uo3qaMvgw9ID1TpTMKhxcbIy4p1y8Ew8DLKUEKkmQb7wcBJ8hJiPKxDcuWakJOkHk2fHKWAlLjHr7jo0IuMiJWaqtzf1Kzv8tQT0VcUKwue/Rlm2P0koiRIJ4Wk2V4GJeVwnd+53e2SdaHiuyHV3OmXy0UCoXCYQC9Rn/TwwjEmDccOVFKQihImD35hsiMcA+9yjOdmisIjNAQPa5GirpZQkrXXHNNIz3CRfQvfSupVjJuYf+hnyU2Z7yMnRwji3E7buULsZ2bOAZnrcTFCxI4NVcQlbj6CL34pUmgngoSgKDotF/7tV9rRW8AKZBN7hp1XpACsVEHXyElarvIPSHknuHvnim2aXs10iLL3LZpk8l3PQc5EVcFE8d16rYk1GOQ3BsZ4r3hxhwOFDIzLNWMcKk46Bk9WSoUCoWDDHrSh961gJTb55RkC8DhIYWMnRARw5ccFbB4ZQOGsIClp4WU5KBYqNLpfi/nkO2g3xUZTR5LYXmIQGTRDxbabGLSI/wsBSJbytkyIT62jE2U7CzBeepQylVi7cSF90JSFgHk2UAMvLh/czomUsKzodMIsHMlkBqCqpof16LdPwRWbFQVQ6QBE9TZD33oQ9spnbwsJgdWiJggECYP5m7QXKtUcQreBQZGrgoyZaWgzUiU9qnqa9LU1uhCoXAUQacydgxaDiu0YOQxufe9792MWe+R5r22EMzmhh7Ro8MNF/Q9HWyBaZFIf59zzjlt0cgjo/q57c0WuYVp6NeUBgE/s2X+H6KSjSZsMBKKnICcJB6uHDQ8BFIpH3TsQMpVY63ExcshE850QA4+9alPtY6KYD7gAQ9ouSXxXCAviAVPi4mAqMQthcAoSCTuiYwgInJMkCIF6bJV2bV2CjlxE2MUYxUvRZbcT3IYYpNnuh55ci1mb+J4jjY4v0HeixoBhUKhcBRhgYhUqI918803twUevOxlL2tGUdHO/sA9hT0VLpNkS6ciOAGvuNU8j00gRMRzg6jIJ6Rv6X2/O/vssxsByoGJhdnQ16IWxgUZ1P8iFOwvwuL/7CcgNTlQEVy/aF7ourF24oIwSGwlgMgHNg6EW2Eg3owk3mJyfv+0pz2txUG5C8PssHpEQv4KBs4FiRQJ5fjkzAjXu5/TQXlOeFd4chAVZAlz50npPSgmneq6YnhpH5KjqiJytC172QuFQmGdoA8tOJGWL33pS63aOd1LzzKATgrmjZGXQnfTvdGn9LMCcharDKK/WzgiIbzvCJDredN5bh74wAe25NzoW3+rRePvgx3jDem9VcJpSKX8IX2MEBojZBMxQVgsyv0tOSyz0hiMTc4CHNo9RLKvxbNOrD05l/Ax/kgLYhA3ld8hFn3lQjklfo91D4GYKAyHfCAUmKLOTX7MsJMRInE5pEYMzzWeN2TtBoE7UgEjEy7tM+l8f1MDVSgUCusGo2dVzvAhDUI+SIsQeu8l4TVhDOUCCrtbICZvkA6nT3nQ6Vseb0ZT4i3vNj3P661YHL3c5zJuqqT8NkB/IhXp5+RlZmeVkI6x6Td+uNbv2S02kcfFz/p7Vv0zdlNfp6I9wsiepq6OcRvujuVoOHIl/3WOztpLjBKJ0LmLJmdhj4s+04DstX2FQqFwEJFcCCct2xzBQCIXSIsV+xiy6LPIY/D6BR5PO0PHQ85LwKjyuMQYWlBKtEVcLEo3kfC5CeR4Gv/miJokMCMtwjySm8HuVF4pJBL8TarEIsVV2b5+0R0PSqoA26CCmMamGgsRDuMhl8V4LlqCZB3YnpYUCoVCYStglW7H57XXXtuMJaKRc3/GkFIRchSFiXjTxwydlXuKd/Z/93NSAY7SxgcJspJikRCERNqDQqYg5JadPYDQGIc+0XYR0qI/hd+EfBKNQEwcW5Mkat6t5Hm6HnkxJkm12LYxKeJSKBQKhWOwxZmX5brrrmuGVN4E9Em1PRg2RlBNFYm5jCQDOYb+xOEeDORhLdSJYOhDOUCICk/K5z//+fav/8tHsQEEKUFUeLcgtc76LeRjSOKy6ADyoX8REb/zf3+XE8obhqjoa/9PuRD/d91B6v8iLoVCoVBoq3dhHCt+heHknMwrnMlYCiHJSZGAK/xzVHf7ICj6D/kAOSkIC4Li95Jm5Vf6vxyhnH+HEPKuTHlPsqlFKIe3CtnQx0JyCfkgjvI4/d7/kUceLIQkxET6wyo3lvDSSdgW2lp13bIiLoVCoXCEgZxY1TOqknEV6HTA7CzSklwIuzWVt+Bpmaqce9iQasGIBrIiL8VHGM2OKecqAXKSAyURFH8fHlkwBK9HEl5TRT47e5T4kG/CwyUB2v+RlRAbXq5Nek3Izgc/+MG266xP3F4FirgUCoXCEYYET/WtXvKSl+z8wA/8QFvZp0joGJATq3mFPk888cRW3kLY4ajsthTWsa2bl0SiMrLCy4C8yFMR/oEc1Cvkk9OxZwFhEeK5y13u0v6viCrPCa8W8qKPE4Lz//7Mvm3IDUJchaf0w7x33SuKuKwAEq2cyyEj389qH9TupEKhsCnEcKqESidZ+ctzYGR5BqyUufkZWgaT8bTTRMjI9tqEI3hYkBa1r5SpYGiVldi00dwv5CgDfSXMk/4CnhT5KDxT+oTnRf8hMrwqvpfdQWPQR8gH4253Fe+IAqsplqqPbR3Xz8Bm+D9vCmLi7+vqZ94h75g6ZkMoDUJ+eHwCckFuHP0gzLhKFHFZAVIS2+DP2z9fKBQKqwY9JOdCeX4EBXERbmCcGWQfK2U7iBhIoQk7TxhmtVlAHgujlNwJRvcgEpbkkmRXDl2NfHhXXhJhDgmyCIq8lFSW/cIXvtD6sN/Z0yOH+iaPBPHIAb1yU/wfaWHssxWc8b/Tne507B4hKJuGdyQnCG22XwfekRyQgZ648Lh4LzvKJHWvEkVcVgAT+rGPfWyL+4r3ccHWIYuFQmETQEicOyP089rXvvbYWTRTUCCOEbeqFg5CYBCfBz3oQS1EcdDISh+mYZBDPCTR+pm35Cd+4idajoYEU14WhfZmIX2QkA3I+RHKyRZjHiuJy7xTDLyCe4jLphBv0qwk4HyQJyFEu59ypANk27u6O8PQYL67jtOii7gUCoXCIQZ3/w//8A+3w2qFOhYBr4My/FbW3P9yKbKV9qAhpe+RFYaYdwkRE8pnnJNsi8T4eewwyB76gieFERdWQ1BAPgovFsIHiIw+cz3vytQW8XWBhymRgDFoqzb6aLt3M/68JyF+3vv7v//721ENmzyVu4hLoVAoHGLIt3vnO985WfF2iJToP+WUU5ohVv9jG8IXU2BUEQ7kRFiDd+kXfuEXjv2dR0UCLaMtX0W4hxFH6MZq06TomlAIQ81LIpcnpE1IRHiHoedNsdMHbE/WV4z+NoI3Se7Ju9/97tFQF48QUuLdjLewjyTt97///Y3wel+eFocY649NErEiLjOQI8FNCgPZH9VeKBQKBwFyNXLm2hiS9MkzYUeRBFwhogc/+MGjh+ttGvGK8JqoKis/xc/yUYR/ELTk5YD3R2TGaqXEk8QjkrPxeEzkpTivJ2Ee5yeFuEiwlVDr+lWGzXI681QBurR9Ubvk3fXXe97znkbw+u3uSIh37s8F1BeIinMFkV/E7B73uEc7hyqHGG8KaycuERxCZFDSeQQge9gTK5t3n7i+3MP/E5tLWeP+HjkHomfY/TMjgIkBmhjyUiSv+Q6WTaAT4z2ILtNCoXD0IM/COUFyW4aGm65EVuhAngmrbXVZlO1P8bJNIluJ6fic68PoIiuM8Cc/+ckW+pGTI09lmEjaIzYhBwn60OsMNE8JY/yd3/md7eNn27z9flNg23iH5NyMwbghVovmzfAMISIIGZLX513aycTLRk4CMuHaRz3qUa1f5W7Kd0qRu01iIx4XAviJT3yixRtzDgOXHKavY7L9axYItNLUsp5lfSMaJiF2rLaAQeqL8YjrEfCbbrrp2GQgsNxj4nh+DhAVRZjEQA0wFyTXGDcaxonAbDpeWSgUCosAARkaYPrVIuwhD3lI03/0phALw0bXbUu4gy5GqLRNaEfIh94X8vHxt+zcnDqSALwvw5u+8I5yUpx8zGgjAIwx2+OD3Gz6oEekhXfkNa95zejf2aKHPexhOyeccMLC97RbzKaRG2+8sfWXfvOu55xzTstbGUJf3fve9272VN/ZBbUNydlrJy5YHmasPgDiQugQDIKFWSIUyEsOfBoiGeLu8YEPfGDnve99byMlMp3dJ2Gd+9///m1bluuxcUTJVkDZ4u6N6LhexjRWmZLIgMWLAyp97TptE+PjgjSBrEZ8Z9OrkUKhUJgC78RP/uRP7nzoQx9qibbxttCVWWFbTQt78DBYVfdl5NeJnMsjWZY3RchH1Vn/Z8DpXiTF//1NW32GuRq8KN6FgbYYZmiREsaWPWCIvb/3tAB1jetz8OM2QZsskNnMJBFDSvinJswy0BeIjkW8aEJOhpaA3W9tDpKI/C3f8i3HiN02YK3EhZCJN8pw59EwIBKAdIYteH5nFZDEp6nYnZCPmBsigoFbJWDPCMynP/3pdn8MUZEf9+CRsRXQBMYyDQLh5zq1X/8BD3hAE3SM3OR2fLiS18iK5CRCj+UjPb7nd64t4lIoFLYRjDoPhQWY5Mo+54O+tSOEZ1ptluyCWWeRTEaYvu7DPv6vzUiKnBxtpm/ZjJz/MwQdjGhpe87q8bP3E0rhWfF7Otxi02K131mTQnM5SJJxtoBlrPeq3y1yvRfCNQZEKqRqDNogzIdUsD36gX3yDnJuhLSW3dmTxGIL+2wNTxL2rCjClCNhU1grcSGshNREwqIl+Zx++ultIl155ZWNdKjiaD89oRsjLgSN0FlJIDuE9LTTTmvuLN/jtSHwCI1J6e+u839EiSA/9alPbaSFuwxZUu7awCEjQNA8A/nhQtNmHiLbwrQvAlQoFArbCEbTTqK3v/3tbeE21FeMPV24jhU0nZ2dPwwlT5B/kRSheDqVHraotJAMiRgixd2STOx6/1p0SipljHkghP0tWr3b0HNEl7MR7MEYGO9UCN4reDVEBSyC+/5Pns1FF13UjliYIi4IFHLDK2bhzCYhXdroe4hLSOcy4EVBVhAj/S10FEK3DPqk7iBbyldtH9ceKsoJmjrKxLnXve7VficRimsQuRA+mjrgy+91tvBPtqPJeharRIYIq+8b5JyZYBLLUyHQBJz70OTgatPBwk7aMURIUtpCkEwMglPelkKhsK2w0rdAFGIYhlPoX8b0sssu27nkkkuacVwl6HTtQRh4vpEVBo5HO+XyeV6yKWIMDCRdj1TQ9Qz2zTff3L7LFiAicl7YFYteXnWLYlV+e8QD/4IXvGC0PD8SZBH8Xd/1XXvW8RbD2vIrv/IrrQ9izBEHdoTdm/cMC28kyjvrQ+TCO/hdtmHvBmyfgoLuOSRWi4IHS39xDBg39yBv3ndWvtF+YK3EJTt2MmBYv4ElQGKOSAchnFUiHxn56Z/+6eZKzK4g7q+wa58cz64TDbzSxQYI4RDjzCmaudakyZYz7RIKMrk8521ve1u7Bqnicjz33HMbmy/iUigUtgmpTWJRZhFn44FFXpIwAzpQaP2e97znnnfN8JYwXBaHU2C0ERTX8BwI+ySZNiv0HtHpDCOCQu9abFp4Ii90Op2sJokcRTbDIYcBg+663hMQ0P3uw7tuwTr07rBD7IL3GtPx7stm8djnyIApsCsWvu7Tj4E2CL0IieVMH/dCvozb2H1EE2Kj3Ou2225reUt7LdHh/T13N8fSIF/6Qt+nL7QxMrhKbLyOS4r9ENacdDkLOghjnndstkmC4ZugBER4Z9FEJhPG5DAhhK8kSfnZ9zHfsYz7xGz7FY42EsRlXXCFQqGwDBg3+s6pxTkUkMG3vVXIwu8YluzetJvIjpS9Ehf3ZkT9OwU6m7GlH2cZejZAzoaFobZ/0zd9U/OYIC3JhQTGkU73N0bSIrbXsd4RnC0kvO/5PXx3aktvPPRCbGPQFl6GnO00z1MRgtMjBl54TPv8372++MUvjhYJTB5OvFH60m6jbGrZC9wTkeSBQaaW2S3LIaAtSOm6Uyc2TlyWRWq1zBswwsdlBYtcD/EGEbZMfq5JJAZZQkKuvvrq9jvMvCdaJo7Vjd1LEVQTFRvl/dl0wZ5CoXC40Nec4smQiHvNNdc0PWQljLTIhaCn6CAGUAjlMY95zM4jHvGIhfJbEm7vDVPyVfzLaAn5pKzFbsF7boFox4vCd7wmdOaQXNDDvN+8BNrQl7wI/N5C9eUvf3lr17C2S0r8j4Uz3DcehDFYtEoZWDbPMTteY4fYmHlnRg2/n12voH1TbVwWiJ4FvtSNZXYp8XYhh0hg+iKHVu5X26Zw4IiLSYh9m5izIHNaci7BF2vsD4qaAgEntGq92FnEnfj85z+/sWyJbm9605vabiaJwSZWH2MMi0Zu4qL0fwpjzGVZKBQKe0FKPdBXvB50HBKR3Zt0GI8ELzHvCsOnuJwzaHojOAvyH3gB+tyTlNQXTs8OoL1Cm4WU3vGOd+x85CMfORbKHy44sxPJx/Vj5+5onx2n9G8qn489byw8wr7Q67YIjy12U3x0KgdzFiykvdOyuSm8IGwZUrGqZOpsr17G4yKiEEIckIVbb7117iGVe8XGiEtO5bQ6MBiYO2EcCkt/sqe/EWjJZOKUhJLwmqxci/3Jl1gkrwhBs6WMe88kM9kw7VzrngQpuTbagKUbFIOI9Phkq2C2zg3DP2KNXJf3ve99j7XXvbj/FiFNhUKhMAv9qjbVZLn5LaTkZNBZuSZn92QnCj2nbotr1aeaF2oPeAWQoN5Q+y4D5dl08Kz8iOjzMb0+3GnjPuwB/cvAC2MltyWg1+Px6dvDQ+5vvsMWCDnxBMxLPxDaR3S8ow0icmrcYxV5jPqLPVo2POcdtAexGPMw7QeyY2uZ4nJjpJCNFQJblBjvFmslLslnQRIIJ9au5gqBY9xNMMY/W6H9H7mRJOu7QjRISJKvUqZaITtEiAuRcBAMRCOuRt/BVv1dbNLExX55R1I3hnclbSO8XIIhHu7pegNlYMeYKYFCjnwCk8E7uL4vr1woFAo94gGIMafP6J+eNGQRZ6Fm8eRnelRy7FQyZHIC/cuQy4PxsVBcBPM8C/Sr+4YkIAJ+Z9GYXZ/0X08gvAdCJUfC+7lWqEKoKIbTPehhv3ePWaCfJa+mqBwjr6geXT6PuGS3k/5QLwVJynbl/SYuIXjbUHl2P5BjE3qwyX636s0rayUuBoxLSsE4LFnYBZEg9AQH2bC1WVKW32H1SMnTn/709t2TTjqp7X03ISTQYtY8KGqsqMViQvu/0vzcoQTexOMqdb3JYJK/9KUvbYTHMwmq7HoTRNtS2AdzNOFdq10EnOvRJBSqmjeZCoXC0cXQo5DfTSV0IiopvZBdkfJW6L/kYiSfha6bqkMyhdR12Q9kdZ4TlOlrRAHxECLwr1AL3arMBN3ab2jwjnTrxRdf3HIkEIYLL7yweVdW5VGYggVr6netGoeFsGwD1k5cCPMjH/nIYzFYKwUTFjmwf/6MM844lshqYggjhTn7fcJFhB1TNiF5ZPzd5DCBHv/4xzcvSp5JMBWp44l54xvf2CaNycNzowie0FMy0d0fQbJCMdG5ID3Dfdz7rLPOahO1hLBQKEwhtaRCUqy2eQbkb4yd9kvPKJxJH+ZAQdcNy9q736JhnoBupK+maqQsCwTDVmt600LT/+lez3jc4x53bIGaQwyHYQN/5wH/oR/6oRbiot950zd9cF/h4GDtoSJsPEmztuVJHkNOZLtj6UhBWLffC/M87WlPa9eLW4YwmDQSzXhShJlMaEREJr3JlIqCnuk+7ps8FPv3s/XOBERseqbv98iV3wsVUSC+59ocslh1XAqFo4WEapCJPuFeHghvb58oKleD9ze7K3xXuFh4fCxZH2GJV3e/t5bmHLf92LZK/yrOdvbZZ7ewuLAMcrIM6E5kxi4WBIdur0NrC8tg7cm5CfNg3EIyYpMpPz0sX0yYkQfb94bgocHUhYSEf0xI93SfMeSYcgSJe1I7EJ0+JwVCrpAqLk5t5KpNxcb92DtfKBS2CzwcSEafdO//du3wcGRbcIq8+X1A//Di9ttueVDsUPS9qTpVOVhwXiGzvYK+mqWzkntI39LBdCMS5h2GibeIi4Xd2EnCy7ZJn7AFhcKy2NiuIpMjO3Z2i5xcyQuyCDJBeXYWgXvz3hQKhYONPmQT9FtieTqEr/vKpcgJb65QdLZ9IhpC3PLvQgjG8ll6WDTlJOIeSE3O5tmvMM4YvNcYkBAfupjXxOJMuF6SK2+Rs9z6I08g1ckLhU3iwNVxKRQKhWWBdCAiqUwqbGOnoLLpwFuCtPRFwVKozLVJms0RIcgIA887K0zEKzNFPiSoOshOqLmHnJcbbrihnd8jX29dQLaEaOSm8ELzLAvJ80YjVxZ3qS5r4wMPUwieRaLNFYXCJlHEpVAoHArwYCAZPAzCL7wF8kYk1/tZjoccExASQhwYZcj2Y56VIRhwxtqOw8AmA6Fmhl5SraNBhKB78pIkVTl9di4OwyLIjjbwbvC8aLNwTUJSuylyNoXsAELetN37IFTIVI446cPmiJlNCjY0ZDs1eA/h80JhkyjiUigUDgRi0BnfGHW/UzsknhHkhKEV+nEdYiKPLqfOD4lJPCgIx1QhNR6Jhz70oa24ZICwCP8w8LYmy9fw3JwJlFomwtKSWYfVUj3PR2kFZR14brRDmQVEyc+9p2MZJNlV7qD7uh8ShSQhcEJDfq/tOXF5GMbyN6TGOyBY6W+h/WWTcQuF/UYRl0KhsJXoq2YznDwqjKjaT9nBg4x89KMfbaEWpIS3hZcFKci5ZuBfRpr3Y/gMHpN4ZXrk+877ecADHtDKIfTfA+2zw1EIRZJuDvxDDFyvVokwTJ8cm63RwlJIV4paarPNBUo08MA4d8jvFkncTb6N9iIhyJB7SaQVDtI3V1xxRbtWGAjBEqKyO+jkk09umxHGSjzYNVQobBuKuBQKha0EAqK6KsKi3ofK18gFD0p2/+RcHv9P5WuhDF4FngShjRRME/bg4ejh+5/61Kd2br755jucr6IEQg79G24i0CZJtfJk3FM5fSSA50cJBTsQER7bfr2D8AzPDWi/iuHO5eEVQl7cC/FAMJAoxGZ4uOEUeFeQMiUfeHiQFe+OvPgbT5A2yMXJVuwchudgRiEk/Zb2FQrbjiIuK4JYOoVoBwJFVO7VQuGO6M8H8y8PCiMrtON3yIpr5IEwvEJFKXffIzWfHvKQhzQiwWCnlHxKuCMRw5CI+/gbD0TOMoOUaFAryn39P6Eqc9tOIzuOfE+SK9IgTwTJcS3i5B2uu+66lvSrrIMditr0yU9+cufDH/5wOzeoz4lBrhAh5AIBmspxQTLcx4dHRBhKnor3RpiEsOgbXh8IKRp6b7wPDxHiVwfBFg4SirisCFZMP//zP9/cwRRYEZfCUQdSItTDyyAXhXFGBMwVNU/8zlyR6MrY9smyCfUgEYytxUBfS4XRvv/9798qb0syRRwWAYPO2PPMaAcPhHYhLbYGC6G4Vww/8vTBD36wfZAXbTS3Vep2/fd93/e1d0RueImU7PcuvB+Ijn8dQqec/3AXEqLi/j49eIqQFc/hHUmZeveSZIs4eechKQt8F7HhhUGi8lweKoSLh2bqu4XCNqKIy4qgMJ6VDyV11VVX1YqmcKSQrcMJd/jI21C1Wi6I/ArJpwlZICyz8jnkgAi9KBOPNLz97W9vpMD1PCb3u9/9dk455ZRmnJdBqrgiHDwYSAavy8Me9rCdM888s/0t+SnaKAx00003tX8DoR5eFIQKAfId7+Yw17wPT4rPMu3KQX+qgX/v935vI0e2LGcb9qLVZpEcOTi8UbfffnsjL4igPhXeeuADH7i283oKhf1AEZcVgfKyUrJKsuOgiEvhKIGRlsvB48jzKHlW6IcHhUdCeCJn9iA3SXy1QweRGRIYO3OQC8QEqWB8eUiEahAaB6suS1p6MOS+LzQkZCShdeiFSFhrLIST5GH/8h55/91Ww5UPwwukDd6Ll4m3ibcFYeEpWbYIHK/MU5/61J1HPOIRrd9TjFMoTYirUDhIKOKyIlAsKfNdRwQUDiPiSfGRi8LLwKvC8CfkgWAI6/BK8Fi4FqmX7Cocw6AyxkI9iIgdQpJks8PH/BHmEIaRIyKXBcGwNRmJcFKyHT88EclDSdsgu23mzUHeDURFaMguIeGV4UnF2q0t2jAG7X/Pe95zzKOxDNybh5Z3hWcFWdE3OQB2eNRI3/eLJvDqc32XPnK/hMFm1Yzp+690WWEbUMSlUCgsBAaPgRPSYaQRBwSDF0UFWjkfcjtykOCYUUUQGGFGWm6FkKoEU4Y6uWC2J/MKeB4vg9wVxdKQmxhRNUb8y6jbPuycsuSV8djEOCMQOQdtinDk3VzL++ATY+7f3CsHs7pftjL38Pxbb721kZ5l4T3dm4fFrig7mvSV0JXPEPo1OTdp56pIhTFJvZdCYRuwduLSK7KhUusn3rxJmO8ueo+x64fXzmrb2DNq9VE4rBibCyn+JuQjR8XuH0mm8rgWrfKa7ctyQnwYbPkXcleEgnhSrr766kYCEBAk4hnPeMax7chpC2Pqeh/w/E984hM7T3nKU5qHJwmovDAveclL2m6fWTVJUhCuJzw+5ngOWASeC1ukhbve+9733uEevE6pxrsMkB0eFm2XwzMPniWn5v3vf38jfDwnY3VY9gNI4oknnrjzxCc+8Q4HRRYKm8DapZACMOm5g/sJLlGMW1QsexE3q9Weld2P/uiPHvsdpULRSWSTwNYTC8+S1S/+DHFBU5Rxl1KUVlHcz8PVVA9VNH23iEvhsMJc4E0R9rGtH2Hws5CQcBAvS6rRMpgIgvlrlwrja6svwzoPQiS8LvI6wLx99rOfvfPqV7+6zW+7ZjybzkjZ+TEgT+985zsbqerzybTvta99bUsInnXGDr3g3XLCs3bQJXSDXJ38PnpCH+wVdBBPhvAUL07y4RbRK/pEn2kjwoPYafMqgFzyWNXhioVtwVqJS8pz33LLLU0ZUjIUA4VkwqpqaYJYGQ3jy4EJ63qK6gMf+EDbWYCwmFQ5G4T7WKzYRPZMivRDH/rQzkc+8pH2s2us0CgNClj83M8UXrY7WkkOETe3Ik91HHvhsMCcQkLIP28ITwrDbK5IqkX4XcMLIn+j34Zs7kkkFeIwL8xd93jpS1/a5no8JIysOTc8qdh8UocEOVAozVZkzzHHGXDEQ94IpOjcGISIUhdlWKtEAq95HfIxhoSdslMHaRP68r6phpuEVu+7SM6Ma/07dpyA5wi98GToN6Gh3cJWaASGXisUjgLWTlwoEKWsxYi5R8V1raZSDVOWu3j1FHGh/CgT5EI8mcLlyrRyQ4RsQZSohwDZ1UMB2oL5vve9r7mmcwYHwmKVRVkiLRIEKRn3d89eOVO2iTNb2cxa+RUK247kR+R8H/KNoJB5hMU84aHkYTFPLAqywBjujvM3ngJzztw1p81fJKAPv/q9nz2zJwHmrd8hHvSAn4EHhyeBgUecPHfevGPAtTk7fzzD9+3OkTci6XVev/gewva5z33uWFG6HnSEXJlZuwRdg4ik/d6Nzko4TV8iP/J2Tj/99JkJv+C99Y06N641ZvopOxcrfFM4alg7caG0kAVKwjbG888/v7lxuYYpT7sK1GRAMMZA4SrsJIEPmbDCe+ELX9hWdMjJJZdc0kiNk1y5rU16/7eKpEzFxF0jxPSGN7yh3QvZUcyJ4qUYnvCEJxy3MuQd4uGhLFIrYlXx5EJh1TD3eEPUK+FVELY1BxD/ITlATBhVZASxYYB7MKK8nuY0Us9YQ7w0YK7k/B6LBITAfZEZHwXn7BjqT19WQh+SEOu+85JezdNnPetZ7dk8Jr7reX4ngddiZhaQEe/4lre8pemLhJX7fvMezkqaBf3FA0WP0EuXXnpp00HIB2iHnVBPf/rTW7/OIx70jgrcPMzCaNpm7Ogh+qyKWxaOGtZKXLh9EQIKgFIx4RAGE5qb0788MZQgJZeS1T0oVoqPgqH8XMNNGhevVY0wD6VDOSMrVlDubXVCAVrNUYKpX4AAUQ4560TM2XOs3LSHkqCM7nOf++w8/OEPP+7490Jh22G+Mcpqi1gk8CbwAuRMnHgUp+qTmBvm3Njfk99iLvs7wsBo827koENznUfG/HOfG2+8sXkkeD5dZ+72YRrInPVdi4lFwiAWKhdddFGb/9qhXYy7vLl5lWEREn1y7bXXNgJkzs/z8GQ7sQWPZ+lH7VYLhp7g6aFTnvSkJ7V3f9e73tXeUXVfeXKL5o189rOfbfk72qVNdBuSiShmW/milYILhcOAtRIXqzUrPErURPNBCFJUiYIUSqJMKb0x4hJ3swmcw9O4TKMA/B2p8Um82/WeGaIT17fv+XvOHEl57yQKIlrCTGLcFK/Kk1y85ZotbDOyDVmYh4ET7mBQyXk8CeYib8mUcUbOGfMQmoRwhpBHxkOqgBzSb35Jgk3Ce04sRlTMdW3KwsEioq/Yao6a+7ygKtNqc5J35YEw0rNCKuYtzwrPTXQMwpI6KFN95ZkI3cc//vF2+CFdkOJ4Y+ANztlA3gtB8U5COb7LmyLHDlkBBE179JX28zRLZNYm/ZGFER3TI2RTu2wY4JHmdUGQjJ3naS8S5H6FwlHBWi0wD4jKmJTl2ArB77NTYdHtlXuF8JXdCxR8D22gNGw3pNysDO9617tOFpSj4L0fL01c5MiTXIEU0yoUVgEyTO7MH7JGDnMwIaKCsPiZPPNiMLLz5hhZt4gQBpqVz8EYSzCVWL+IJ5KX4Qd/8AdH/+YdtNV2aOTF8xEXRll7QximgAgk/DQPqT/jGYicrdRye3hYp4CA6Tv5MgiShY5QtTZ5tvbr3+TMBbxR+tN70B8IDc+LNtCHDlwUMnIvBCZhaGQRYRGm1i56BXkJLKh4cTw/nuRC4SigXAcTsCIVy7by4/q2upqlGBgI7lzXxyDkJFuhr9qFVFgVyBkDaCXuXwcF+h0jx2sRIo0EMJBCKggCoz21U0d4Qx4ZwjPMa+nBYLvnoufmzIL2CIvIt0k5AoTFbiG/V6Ruv+aRvlGLxg5H78jrMsvLAkiFvrvgggta7RlEql/E6N94a4cYC30jOnY7ys3jJXLOET2TRR1i42wh27TH6kohlPSO/uHV0bZC4ShgrcRFnJqS26bEVm2xGpIA2IMStcqhzCiNeZUpraS8n9VUiEt2QlT9g8JewKNi9c17x6AjGzwhCEU8J6lB4kN2yay/MbaMPQ8BwybUKTzDu3Dbbbc1QjCG173udW2bsqRZ25GnCjIi5hLq5YvtNUl0qoT9MqXtA7sU9Zn8k+wW1C9f+MIXGjFC8FyDwCSUPAsIiVwZ5/3wvmYX4izwHiMW+tz3++uNnWrD+s64er7cH4ceCj9Z7AgL+X6/w3EIsiBnydgWcSkcFayVuFBu4rhT8eYYf8p2L8aeZ8QnxZy4s3tvSVzr3Lr+TpEPizfJC7AqpfCQGknEs0DJWzF5v9RsiCvYaq5QWATZucKokh/GlkcgxAUZYQQZtiRpul7YI8Y3Mk9mfXJgn0RVv2dAeQtmeUkYd9dPzdVAe7SDkd4rkH6JpnQA71EWANpgji5Scl4f8HrKC9EnOQ4AweJBEhIyJ4VZ9O+ih5/qMyGou9zlLq198/LcEEz5fO94xzvazh+hNOMASbC108i/9BCdoc1yeYyLdvkkRD0rOdkY0z+FwlHBWokLhcvdS2lSdAw6pZzKlFZs4rzi4Nyu2YVEOVvh+D43KgKEiCRpkBKnrCkjhMcK06olibhWItk+zXWuVgUjkOQ/12bXAcNBoWmT3BdARuYd+05xDJWHtmcr9X4o9sLhBENGVuIxIcdW4ymeyBBnzjDi8bL4v2sT4jA3GFfybx4x2OYJYiNp1L2AjPs/g2nOuc8w30Xip4/5gTCYX7POzdkPmN8MtURf81a7/Esf5EyjWTBveVDUdxJ+QVzsFLLw0E8ScPutzNkV5Ll0hXGgS8Zyf/xdO7KRoEfOZUptGpsC6A6eKl4U3hXjEOJCn/GYISr6M9XEtVVOCz0iXwjZ9M50z6wTnD1zbCNDoXBYsVbikoJQEskQCas6kxZ54eqmIHkt/J3XBblQ7fbNb35zU2aOZHfgmjL94tOUO0VlCyMlZyWVCryuT9hGlj+lQJFIZqOsGQP3pyAk2/XExCooO42A0tmPGH6hMAYGV+hGGEO+AtlDZKy+5T6QX2ftIC/IBAMsn4phzpk8wLA+8IEPbLU+EHFyLN/lqquuusMzGVrJona/eGaKtg2B/CiSxuOg3gtj28O8QAz2w3AywLwHT37yk1vdEgsM95e/IRF23hy02JDYe/PNNzdyQLdIrk8hvCHBymGPti6rG8NLctlll92hL3zf351RNOYJRj6MA5KHOLpPjiBAKo2txZPngMWMdiXhNqDDeGG8L8+T3Lo8v44XKRR+H2slLlk9qXNACSErJjCvCa+HiYq4IC0mamqpUEJWIa6jQN2DEjHpxeitUigI9+Qatt3QSiVbMXl51GBJZd1U3KUcxJRts+xd4tyyyA3ik+qUVSehsB9AUqzAkQ/GORVr7fixIreVmKwi0j5kMUXeEBs1ShjGeEz6UvLIjrnAs4IE+B6Dal7Jg0gBNGBgzTU5LP5mHrk3YhSYa2QfuUHwfcecknfBsMsfsRWaQd5LyfrAvc19JMW9cw4SEqYds4y39iNpPvon/TIstQ8WIt7JmWYWOXSFd0ME9ZvFkoVNdhqeeuqpbecUb1DfhlS0fetb39p0kzCSargWVD760vONOb1jAfaYxzym9RVSOgz/pCaO981p1YVC4Y5Yu8fFpKSYKQorjrieubd5SZCMkAjKyurjzDPPbEoc0YjXRtw3ZxLlbBPXW/1RfMnuzzMpKN/jXUF4KAnPtJpFhPrEOd9NGxEXbSriUlgUWUUjDYwfOc9WZGEbRom85twb15Mx8m1XiTwUoQ2eF0bY99QT4lHMIYJj4RmGPqX6wf0YU/PBHOF19F2eG7U/eGcSjjD33F9bPcO8MT983zXmlnlkqy8PqXfwdyEcz9mv2kZZ3Myrcpuiesga7616Jkl0HYM+9Z6IIS+S8K+2I0g5Wdl81y88vwig/vK7Rz7ykY1o9HlwqZPDQ5LaKsZYm2xv1qZ4w/SVe0mGpp/oF3pH346hCsoVCrOx9u3QiABlYQKb0P0x8pTHkEDwoCAdFKm/ZcWDyPDCWOHEDZzv99cFnkkhCDcFOTSxh+9R0rw2yEu8Ntu0E6qwnSDLyAMPiqRahg0Z4C3JLhchFbJr9c7bgajwMuT8IETete9973ubIUYSyF7ytZDvPjw0fL5Pii16Bu8mYy3nwu95e8y9xz72sY3EIzEMuR0z/ia8xMj6PsJiYZDaRYy4kEfCKCkAuS5knqdQHYLmvRAHHo2+xkmgfSFmtjALNev/9GcP45C6LMaFBwqJkV+S3CJeFAQG8dRP119/ffOeaQ/i4u/ZjTjMiyMTvFUPetCD5p6btJt+GSOz0VsVaiocJmysjsuQpIwhpGFKOSYZblEkGW+/2lco9OBNYTwZ0be//e2NBDCyjB8iLDQhr4QhjNH3b0485y1AVuRhMYZCPWRW+AB5ZzDdX47ELPgOw4yYeKb/qz3iPnIvhI6Ql5wHFjkXwuBR4c3MQmE4B5adc/sN/YRgIXZqnDjnyO+mjiPwjnJ+LEKMwyKLEH9H2hA+P0uw1S/6TChKBW2kVBuceZbkaL+TFIz0IEnDarZCQ+6732cLhcwNCa2xslCsSt+Fw4aNSfQiK4B51yy7iljm+lqhFOYBsbCKRiaszhkxYRZeEStqCbXZbSZHhAeRIQ15Zmx8n9fANl15Fe7jHgyxxFweDwSEp0PICLGZR1x4B4SBhEMYLYYN6UGeGE4f7RnKeMjKLKx7XsSTwBPFe6Wf5I/wROmnYdE4xIRnFYnkSTr55JNbLo+k30UWLXk/9+EhMx6S+hEAnhhkideEZ8u/Q7Jg3Hh3VAcehoJykvYi5y4tA7lPY3LBg/S85z2vEbCqqls4TCgqXigsCCt7hko+g3CAPAbhCoSCAfWvVT3DJX8i21j7FXaSNZPDotZHKjS7V/JeGMnUM0JsEBzGO1v0p4B4eJ4cCuFRyEGHPAC8BrO21m4TUp9GP/f9JKl/quKv/tP3vB7yhniXEJicS4ZYCOmkvMLQGxHvRbaiIyp2XXmeHB/9b5xDbBDRhGjiOYs8GIeEoj3HzznDaT9BFpEW5KUHguSE6nUdn1IorAtFXAqFGYgxym4gBEJIx6qfQfM3HhWrfOEc3hEr3DEkmZSHRt6LLf129DCkAYPLy6IkAK+C1TTDvShSL0TOyrCuUA7922aEXMgZUVMFuZPDIiSUpOMpJDTC0ySXjceqvy+igYzYNYRU2uKchNuE7HjRPDfeFqEhY253Y8oj2KaNuCAynsXD5vvGF9FCJGwbRxyyhTsHSxqD/Q5BC0mmRk8P5IvMktdltqsjYzmYsjzPhW1EEZdCYQYQE0YUeVCXI4f/MULqCUn2RBIYqFn5WIC0qIWizgjSIol3uBpmbHhjhCemaqvMgpCIEFUKKh40pKo1wqC/hd+MwdQp1j30PaMrV2cYjnFfhES+ytve9rYWykNG7bgC1/OqIIr+7lokJtWzh+BBQX6c6ZQDDnlaENLrrruutd0YxvDz7iCUrt3vhGZeoDHiwjt40003tToyy+S5qPQrrMhTVShsI4q4rAAUYA5XtDqbd3hbYbtA4Vs5M0J2jvCQWO0zfpIuhYKEXCh2uSJCAmM72YDBtdPECpwR5qXhSbE6t1pHMJK/ke3TDCYjuBsXP49DdsFsOxAUfeO9eTvMF33OA4VACAnxfCwKxtmHd8bOLKG2wDgYQyEVc9KzPYdXyrNtv/ZdRIXHJNWEp8bA+HnGlVde2cKDPCkJLyG2KdnfX29MeXE8h8xMHci4LHJ+1RDeS3sQtCFZIndCaYjusLCfnVXD3yUEhsCT9f4kcN4c74+8lYemsA4UcVkBKGM7SxgrypK7dl5disJmkSTQhCckXnKxU/qUOJJByecwO6RlSkm7T9z0jKAaLE4Bdk9GhqJXuI3hICt2+iRPgqFexlgzFjwM7sVQI1RqH60iGVNfMPghGvOQAx95rMYKwXl35MF93U9/5Rwh35nVDzltuSdo2amlsF/CManXlBBdwk3JSfIs44lMGnufYZ2cHEHSv5c2p76O93CN/p/ybLhnjkzQbvlHEqj3A8iJvtOuHvrCc5CUIXHRBt4f7R4mLQuf9aQP3Bvp5kXyDn1NGyE5ZSuES6toXmEdKOKyAggBMFKS5ShfE72Iy/bCatIKG6mwWhfOYeSQEwmtKTnfJ1vOupcxdy95MHbBKGbGMFq9MxKUPne8sAbSgtwsetjfEDn4T70WMubeKdQ41T6rc23pjTPDjpCMEYygr9jru/qCQZ/K2WBMeU2SY5EEWc9BGNwLkdBfy5x35LnIBpLWh4SQnZz6HC8nIsFwM+7DHBntZqAl8wq3ICFjNXLkLfX5QraqG7NUGdaX+lWf80QgujlmYAypDvz0pz994XeeheRejREXskBulyUU+s8cSKKyZyDfCv0Ni/wJTab2TRGXwjpQxGUFsDJXbVOSJiUnzlzYXjDEQhPyHyQ6cv1fdNFFx1arjB+FvIgbHGllPNX4oOTdj1HrCQEiKwciyaK7JS2gfbY3SzTNFudZ7UTQhCu8c/JGGFhtZaimdusAQ629IS6InbACUjL2zHixkLV73/vezbC5P6+GM4X0zSyiNAbjoKbKGWec0crw98SFl/MFL3hBu3+AVHgOD8kQCc15d6HB/kiEHs5OsqU6BO3Vr371zi233HKMuOQAS4RK+AeBIDN7GddlIDQ4FXaaCmHOA0/YP/pH/+jYlnPjljBYobBpFHFZAayorECsvFItdZZBKKwfDCZvAK9IzqVhiB/1qEc1wokMMIrzPCyMlJW83UFW4X6WQ+HeFP1wBZ+ToOUKxPsxBgbaVl6r/Vnbl3OwXzwb4Jm8PMOTnBGIeEgQGM8nqzw1PIQMvLDTWWed1Qzv0JPivoyY7yEk2oWkzwpL9RWvtQc5Sgh1WdISeHYKyeWYg5xD5h36PnUtT8xYrorfJddlFsmQF6Otyeswvn0YKzuhcjp3zlmbuqffe3/t3S3IprHyvLGx2isQPTKRUJ7316+lxwrbgCIuKwBFQrFQXv71/5rw2wGGjuGxO0jMXviDERR64LUQGhIWWCRHROKu2iJCDDw2VvqMJEU/tsKHRQxAKjzbXq0eS7bpMpZW+dmWCzktGklOgiS587ucL+Qa388W3nhmyKVrraIZfuEbhhCBy/k9s+BZwl09ucs24mEejD5nrJEMfaafdgP9x6slxOZZCAPCmG3q3nVIUqaOSMhW93k7luwA84zkdSCd5GYIz+W10a6xe+p//YvwkUPvsFsgjPpd/6+iMq72I5o8UWSnB+9OT6Z5KPfjdPBCYVHMlPiUkTbJfEzIrCIoLas3CtOqzSSqEvmFbUTO7xGn90E0hIV4PpS3V+XUv2SYUcyZN2Q8lU4ZB3OAIo8nQzhI3N/9psIM85DdJcmFykq+J7+IQJJc/ex5geu9BzIibBOD4vvIGBLGC5FqvN7JnM2uEQQLofBsc937I2EMkXltTiNZ8dS4h+9ol/5KkbyAQVf2Xj/1hMF9GcDdEPj+mIHszhHe4bFAJhA5fTB1b22PrvL+Y6QsOm7MM+NdvHMIWnbp9Amqaaf2IYxjXjJtEC4zJgjHbmUGyM3UYZurhHcUQuUNDPxf+K70f2FdmElcUiFUzJ7b0G6LxI+tTilGyV+SF63ShpnohcI2ILkMV1xxRdtxwjjxrJx33nlNdrncGTMJmmp4MIoggdLuH+f9kG9Jn+94xzvazgpAghifqRX9IuBVUd2U90ftEqt5RIuRl0vxpje96Rih8Xtt70MQMVyMq7/13hieDb/L9/08LOufHVDxkCS3wS4lRhZ5klisBgljSycgNogUA2xrOEOdPIp4dng+XNs/Z7dGFmHQ/9n1BUI8xlCui1CfcI5w2RDeVdu9S7xq/j/0qPGe0W9jZEIScLa/Q7bJD/M9ECPeB3IzVgOlL/m/1+3q7uUe606G9Twye+GFF96hLUVcCuvCHYiLVQeXsUPilNk2OSkhys+kjgvc6o+7nevZJOW6VPHTypVCmZpQWf1SqoxJYDIr6IQILQL3oKQpUcQqSuPrv/7r29bVoevSSpDSY3zU0/AsW/gosjFYdSNrrqeAKT4Kyaq2JujBAQNjl9CHP/zh5iWQZKn4GENkLBldK2FyqaKq3BBkHZAB3gi5KkgOOefqT1JtdufsBYjK6173ujYXyGfyPrKTIxVZ/V97yW2Ky5mT2pddNOaOOjM5Td0nbX3ta1/brs022FNOOaXNCX1jDgU5ksD8VVjPylo/eG/EwZzg8fE890L8EDseEXPGriz6I0RrL2Dk9XnCQz5Bdif520knndS2FmvnEPpP23lHvFNOle5DOb6XXKcxEioH6LTTTmt9C+5lJ9fQw+NZCBEP2rAOCsRzdBBOmydrl112WSOIfV9ptxyw/T5vqVBYBscRF4oHWbEq5QanOE1EEzWfISg5BMZkTIIfRSapcHiQG2XjegqCO5nbO6AEkZ64zqfitlm1eY5V1gc/+MFmaBifnOB65plnNiXunrmecma8UleDQoyLnPJlDLKFkeJ17/e///3NmCBslL3VqJ0MVujlXdpORMYYa6SFQfIhm+TSWNuKbPz7HRe+ZyXN65JwDWLMg2A1ea973asZOHOEAZ3KYVkGlD9PT2rFkF2yz2gECI02aS/ibFGQU53JMTlFXBAoCeHeUdXThHXkfcgvCbJwyN+nwivIuucgLwyX+eg+vBIxZimUp83617z2r/mzGy+UOaVPkAv/GiuLC7kgCN6wzy2qhIu00ZbmqUMUjZ/xzfEBCFvfPjqAPjHXx7xCxpznLV6ao3BgIbLnncfI5yKHVRYKq8Rx7ABpueGGG9oqjHBSpIoLTZ29Aia9HRVZ+ZnkFC2SY6XSe14oBcpfyXMKxM+us3qjKClpblzKd9b2U0qT10SeAtLE28OYxJui3ZQu74tnUq4S7K655pr2XUaAUbKlkWJ/znOe096R8XA9bxDihrhQypS767wb42DVXsRlu5BQhLFmhBg7u1fINNlKES5/Z4CN9bAuC0M4DBX4rkRX25fJQMIke0FW5sIsvJQ5DBH8TP6BoUZMhK9cx6vgO9qMNCAIPczZFGbzDO+CqPOeZusuUib0456uYcB5KIeI69/Hfc0BRJBHSv8hPeaDeYXIm4uI1DCRc1Y9kyGMkQUHnSIM9aAHPWjnhBNOOHb0QV+tNffWBkTEXJ/lBaAftP/1r3/90p4gz96r9+igwVw5CgStcDBxHHGhkCmehz/84W07KK8JRTIraz2nqfLOxCWPFFg1UXa98FMAlC1SgLRQTI9//OObcaFcEZ53vetdTUkjBmPEhQKhkBEWKzwK7sUvfnFTyJ4tT8D9ESAfREW7UqraqvWSSy7Z+exnP7tz7bXXtuRKKzvK3mpWG3lx5BwIPTmLhKJ3vXeyorTC490pbA9yiB6ygmQ4n4UckQ/yydiSDWSUoTauzhnqjSHCK+w4LFTm/694xSuOFRrbK8i2UIMCZMIPPbk31xAF70MGFbAj1wgTw+59rIYtFsipfwO5Oe7Fo4SYkVveJvOqb7f38Dv5IbY+M/pj6Oeu+S2UhuwnPIYMeL65NbaTRluW2VGX0JO6KZJbk1Brvk4lotIRy+SMHDUCUigcRhzHSHgSUmkxceG4peeBMs4qEvnhqRm6FJMISMlRNDwlXLwUFKUouY6CtmLOjo4heGcYJ9e6H2Uu6c7PQk+UJ48Jt/Cd73zndg+KleGi4BgthIQ73vN9hwKmXLU72zWtdhk+hbP0i58ZMDtQZtXVKKwfvAkIJW+AcA+C+kM/9ENtnG677bZGAMhddo6Qr9tvv7152eS4ZJfJ3e52t7YqHxKXJMvuFZ5D7sms55pb7mvBwNNiHjDESagVTkVOzBfEAQlBXMg7z6j36hN1yTAy/7KXvawtCMwR82DoHfQM89sc4EGcVdU5niyeH3OzP3cri5a+DcnjEOKRa2OuyXvhAROKmZUT5B15TIWMfT81Ucb0wG4wy/NjXKa2gCN2w5O2C4XC5nAccTFBh6uvfispMhEl5/dJ3KWEhVQoQZ9FYDVGoSJHEl99j9Fxz+FWyh6IiZAQxR43drarMgSUkzb5IB/+hpxwJ6f9vpMaFK63+hSmosh9z7VRxoxYtpDKc9HWcqFuDgyf8UmZ/OyE4VUzhsY7hDP5GMNDLsmOPC7GmAcwybmu73fC7Dd4MRFnCba8gd5DGApZVmnZTh5GWnt5FBEVsg7mA+LAmJs7+sH17tODbHon8wQxl1xrEdEDGUCeEIt5pCDkRN8MCd0YUqsE8XjoQx/a5pQ5Qz8gL+ZaatkMSYyxQioRnezi2a9D+7Kjxxzmsc38dn99hsTqp7GkWuSLTBUKhe3A3MpF2UpKmVCSFFBivlZ0FGx26FCUyyoa5IMSRShSm2A/kRNbKasxwuHvDMJ973vf5r4Pktdi+2s8RVZdFFjOSOnf1ap4WKeCgRRe2st22aOCrIb1VfqSsUk9kYQrcwaQLcmp6Ck0yUvGG/aQhzykGXRkhseCB2UIz+CBE1JCeJK8yWMzVlhsN8jOkV5GhCnt5iFn2m67s+MgtAV5Ql6EK8kqj1B2NwUIuOvklCTPaugh8DzvY0FgEWJe7gYpzpZcGguXRbxOIQg5BsD/tVVo1fzhQcrcGibxarc5isC4Zj9rlLg3AiJPiOcnCdjayDMnl0bocL+8O4VCYXWYS1x4IOSM+DhMi/IVWqGQGAyK3yqVYqIAls04pxwZmeQWbEvuCCWd7anIlHdGVvx8zjnnNHd9j+xyYlyykqR89RHDVOGl+UgdEt4QIQOePPkati/H0yekKLEUkY5hS7l1hJLhEUKxxZi3ot9C2yOEtScX+1Xd2NzQ9uwaCrybNgmPCul4T3ko5gCiQqaQf8RFjs6Yh4PBd+2LXvSidp8xQ+t9+tOMd4N4LvWl3BmhuEVOrQ4pkXfm/YSs7MgSCuPtOPXUU9v7SZKlU7x/wMPCU/bMZz6zLZL2c8sw4svbpd+GuTg5bHHM21IoFLYPc4lLyo9LSE3Gv4RBcWjJuwz8m9/85kY+rHSXjQXnnA+EYK81MfYT2mVle/755zel56RnH8mdtkRTxP1qOmeeIGBRjDmXZhGFf9Shj4QK5aRIhBYyJHc8eve5z32awUP+kECGcbg1FhFh0IUjyCRv4LxaIqvyhCFZTmtWI6jPH0FkeBclo7/mNa9pxCknIyM0119/fWsTr4D3HatLkrL9vJxCnfsdtjQPybI22jGEjCPw5n3vcUEseDDMASSzn7uRe7/XXvMoO/14YniD1F7xDq5BiugWOUaIqvBSTljeL0SP1VbeQuHgYy5xsRIRo+bClodiBcstn2PlkRfbm2edz7IorHysFLl1p5RWtpIuej6H6ylIK+AxeA4FTJkmZyZJer7D1S48xlVudwcD4z2HbmwGyo4I/0aJy1VIAbvCNJALhtEWeZ++vg+Soj/JILKIHI6dc8NYSsKeh4ztMO9lEfBuMKrkZQrkiaEW9rHCl+/RQ+hKuCRhqRArZEEIjMdFKEnYaypUEjKwX0bYc3hKhG7Iq3wWu4UQSEQ8MDe1Tx9YuBgT3hNbkoWThx6rJPb2pQ0yx+T7mFd0CJIprCXHxL+z5n+hUCjMtf6UDCWJLFAmDIkVmCQ75IHiGuYhTCHVPHPkOwJgVZk8EPewqk59DddYkSY0FcLCq5My4zm7xM9ZEaY9vuMjL4VRS4l2RiJJm/4uFIHcuHd2fFjxube2+T+Fm9LWY0rVinFY9RdhSSny/diVcljBuMVwG6Me5EI4QbhCOM7qfC9nvORcrd0QF+RW2AOpmNp+m+25kj3H5gNyQB6GhxMG8dzZJr2Og+tShM68RlaEqHyMQ09EQsiQKrkgiAuSHqIjZCwUlhw174fIP+xhD2vkZLizyf9TSr9QKBSWwVziwvgKDYnJZ6cOd72VGCPPwCMWyXGZhSQOuo5y5o7mrUGCKE6rOR6OnJFiFZdETEaDG5nRUKALIeD50RbhG+1yrftTrrZlW9EhG1bq4ucUrBwJ//c+dnRYRVKe6nnEu+STs0gkT1phUuopXrffbuyjDn0ZQ4akDIkJOTBuQhfkcVPJzkgsDwmSmzDJGEJyx+AdH/e4x7UdN2NhrGxTXldIA1EyL66++uoWtrEoGTts0KJB/okaK0LC5oD35Il9/vOf3843UhPJvAbXSkR2unXljhQKhf3EXOKCQIjVW/EiGgy3AnV26lB4/qWcKPJ5CoqiQ0Bcj4wgDsgQQ+WDcNjdY7XmWt4WqzikgbGizBEXhEmSMPJkpYf8IBXu4f4K2yEuIRh+tgJW2dMK0cF1KZAn5CXJMSXgER/5PO4tuVB4yMpXOz3X7oP93KZ5FGFcGUjJmcYMETA+5II88cIxqAEDb1z8nceFHO7W64Lg7jbpk2yRAXKY05J3cw/yOFXIjpeG3K7y8Lzew8W7IgHXXOZl6T1R5oVPijjqewsGIeO00b/GT04OD4zwkoWJUBmvzDq8RoVC4WjhOOKS4+r7nQoUD6NCCVkNUlLcvwwMBUbZSZ7kRqZ0fZ8HxveGq8YceGZ3EuKAGFCgfi9cww3v33wvOS+IjPsmXEVhIlOebQXOiFkhIk+MAo+Mdkb586ZwvVu5yy1gGP2NUnauixVkyoW7v3vz5GQrNUNLKctZ8O68S0Vcdg/kEWnhzZLbYqx402xldj6KcUcyja9xTY0enjDjMtb3KVSWgonkItule8zbbo9YDPNSAt5A8jncCr8MyPNed/zsBTlENeeF8WIhkSFS+tr7yTUxJvpcgrS/80JawOgj9WGEbM1V5EWum/nJm5l8r23ZIVgoFA4XjiMujDSl1q+oUpfhiU98YlN6XPpICoPCQxKS4jrfZTAYJmSH4hquHCk3JIgHhZLzTOBBofx6ZUeBcq2LqQv7+HtWuchG8l64p90PcUFauK+Huy38PkZJ263g5aTYITRcFfLCeH/PQK4A+UGKEKBFE4MLdwQZsnvoLW95S0vqZBD96yM5k0G0Ykc6Qj6S3Mkr4LreGxMYTwmfjKl8Il4EMrFMWImcy4dCaMeAcCep9CAhdYj0PZLCK3LrrbceI4cBEqLvjQPPp75MfpF5bt7wfob4W2jQBdlOjPBPnbZeKBQK+4XjLDCFZjuqVSuSkIMSFZDKmS5ZaaZCJqUl5IO0+NfqjHG5+OKLG+EYW736LvJCyWWlhygMV6Ke7zqrXM/pQ1H+LxfgMY95TLsH5YxQJPlyCPdGPHLwYvJtxlbPFLjrECGx+rTZ74u07A1CcAxmv8o3HvKJrrjiipYvgXT2Z9MgKhJaydVYxVUgs87+8XfhPcZ1mXOFyADSJORB3scw5kU8KEgOGBLizCb9M0xQ5l2xFVsODi8mXcAr5ud4rngfeV7UyUFmzL+pHXuFQqGwChxnhZEMRoOCE8+O25iiG1YBDSg/7nvGxUrXd9RjiNdmiNzDc+bVoMixAFMnMS9TlyHEZ14eTnY+5d6zTpwtLA4hIXkStjv7d+gJ8X/EhLE0VhK2cw0CM897QvbUQWFYVZydV8OlB8+bpFOeBp9ZZ/ccNCAdvCZyWRTt44lKGBTiZZGTwuvJW8nLmdOkeWT6fsxYKI4n9OrnLAQKhUJhHTiOuAiNyFfJkfV2+qTE+pRiotQoL8pPiEX4iAuZMdhkLL+wPUBqERHHJ9i5wnAOkYMMFZAjfzwwU0AmhSiEdnhuXItA87TwsixybARyJGfFfeQuPfaxj21E+qB6VHokNCSxXS6LhFqkxXbyvqaQUJB35/lEXMzZlOrn7ZSkLmQkPIR46tssAITT6IscDFkoFArrwnHEheKiyMX55SE4hZnSYniQk+EKNieq8rIgLHbzID7yVPazXHfh4CJHOthSb9v6rN1ACMciB/kJTZBRXj2ehJCcqQrFqR3U79Yht+edd17LWbJTKCT7IBvhVKEWLkNQzF/nMdmmnLkbLybyJyQmx8u/viP0k4NJ9Y9kaeHSSy65pBEgxBJZlEytlL/QWoWJCoXCunGHhA2rTp4T+SPi3VzGVssSI626eij7LW/Eys33rNay86dQAB47pOWaa67ZVWXlJIjnlGIQohByQkYWOU4BYSGjPCw8CeC7iLrcmMPgZQHkxHxV3whhkbMmTNQvOCwq7BZCWCQam7M8Ma4XYhMme8QjHtHyypASc1x5fuOIhPou74zk+yIthUJhE7gDcckWZB+rKzsoJOZKVh2Wuvd3ISLKP6vZIi0FSLjC+U5IBq/LMsmyAQ+ecAZPDePKk+A+YzuLpsBDIOH07ne/+zFjS855bHZbj2WboK8ROFv9bW+Wx4KMSJj3+9RPEt5BPCScy2MxPq5961vf2ipLK1HAG2OhYheh/jL/jYHaRZ6DAKZA5CprzRQKhcIUZm6RYSy44a3inB8z5uZPzDsJuVOJtEcJCJ6kRsbDbhhG9qgROt4RhpMxdZjgbkrsA6LBeAplLNuHvAmqMQsHqQ/Dk3jYkq3JWipMC8XJEZL3E1hUWHTwkPCeyEvhaUI6bPVHBn3P+MQzI7cN0fFdOwN9z6dQKBS2ATOJC9exHALbV8XLh+fItBv8/+f7XH755a3ORRGX3yt+JkfI6leCJOJ3mHaqzIM8C33AmKpyOyvRdh54BHgAGONFq+VmNxzPAO+CHA65GoclJJTDC3lTkAzk8BWveMWxAynBggJxs0tItWmhnxyeaI4iJYoA2sU1FsKT6KyIHOJSKBQK24SZxEWM/PWvf30zPFP5CVZp/sarMDwd9qgip+jaWsuI2lp+lBDiduWVVzaP014gR4MR5sFZZHtzTvt2PICPMJO8DmNyWEIbSAsPidyh22+/vRFkXpeQFn2gtIH3Rzx4Qq+66qo2JhJshe+Ez9xDqFdNlyHufOc73+HQ0EKhUNgGzCQuCAlvgd0GdnGIiw+rhjIGVnYUXRIfjzqs9il9K1urfFtRx4qmHUYwjLY8X3vttY2wLZOLMgYyJVGcgXVfCeKzCIyQCGMtgfRrv/ZrW6jpsHhaclq5ECRvlrCQ3T62lyd/SD/xlOSgUb83FgpDqlJNDs1nPyOE+sZ1vDXGiveUd8b2cEUoC4VCYdswtwys/BUrNlsjFagahjxy0Jprck7MUYfVvYRmRkFSqv5h0A8zckaV0I5kXKFF/++TuZdBToyWOyWhlNfEvYQ6xkJPjDAvglwWh4CqQXJYkBo3vE/69zOf+UwjIsgGIqevEDSeJqTF+VtIByLiVG0HmgqzhdwIMWU3FqLie5JvE1pSuyUJuYVCobBtmElc1Gmx4uVpUaPFSmysnH7haCP5Fsr533DDDS2EsdvTmxFhxC95GPJT5GiAZF95Vj1xYbRdT04VPnzoQx/avA2HAalSm+q3CKGPkA/k2AqEw44hoSGkwzz1Nx4quUF94u0Qxs29fR9ZkRNkm3TtECwUCtuKmcTFbgR5GlZ5EnS5obntC4UeDCxCgbQo5z9WGXdR2G4r7Mj42vHCW8AAe4bwBg9WD1vyEZXTTjutyauE3MMCHhLnf+kH4UYelpTiBzWTLCrUp3FmkPfXHyEcyAji4zvyWoSZhkj4Sb/rcx6Xw5ILVCgUDidmEheufkaIwbjuuusaeRES6kHJyemwUrNlct5ZQKnuyQDZtSSpUCKhir1c1v3p0LNAqUsqpMxt1dZW+TdycdxneNyAv1PQVuvc7P4uD0VOBHf50JOk4JZrxxKOhwbiqMNYMI4hLYuU3B9CErPQhNwU4R4/C//wMNg1E+9DQm6uR6J5WVwvpLTI+VcHAfrPvFCqX+KtfBb9yjti7pA7XhbelYSFnLTu3fuaNK6Rv3L22We3v6fGS59ob/6Sf2TRVunaFVgoFLYdM4kLQ49gMBZ2GAkFDE97ZkC49Hlj5L/MIy6IgORC26zlK9gujHDIT3BmSs6PmTqFOYXNkB71QSh1p9Vyp8sr4fam0K28kYvAVlDv8Mu//Mtt9Yq4IC1qfMih8Ew5Ke4vb0CNC9eP7aY666yz2jsXcfk9pKotcribInOILxLyvd/7vTsnnHBCk4MYYLJiO3QfHjKuSCeyLBEXWT0sVVyFw8wzBEN9FWGheErMCXOFd0Tisf6S06LvzDtymxAd+URcXE/Gfcf8FFKTNI0IIesWIu4hJ2jRRUOhUChsEjOJCyNkhZdVGNJhJTgEIyOWznAhMFNg4GyVddq0A/eQjNyb4WOwPFOewiyPhmu4vuMFYvi0ATmRuIhoSdC02nQPK3VJirZ286S43u+44XkJPMvvsmMKWROisBtDuxAa908isqMQrGALv7eLyEd/Mo6M5zIeF+OvL9UAUt2WcSUnxhiZFQbiVZPsC8aTx0to6FGPelQjq4eh8q15ph95A1WyRch5sXIiNpJBPuWfIGy8I5JvkRCeRyQcwfMBxF2Y15gg6Yrv5RwyoSfzgaeFx+qUU045Rn4KhUJh2zGTuFB+3PCzdsRQqLwwyoPP24VAOVtRIi4IkJWgc1EASVDzQ1EsbmtKdOx0aUoegUJSeFoQpXPOOacZPCTm+uuvb+EFbfdxjxRCk6Qohn/uuee2Fa1nISlWuIxniAtj4doYYLF/78aQWuEzHuVt+T3ccsstzXtmPPTjshVyJX0LD/F68RAYpxy0aKwRzV4OeFYQUuTRz4dhHHK4pPOceFl4E3n6soUecUZCvLM5471f97rXNRnmYfF/BE/IFHHRJ7wnz3zmM3dOPvnkY89BzuW9CKXqc6QR8TN3DsuW8UKhcPgxk7gw2FzLs1bQ8UKEJMxC8hTiteHuR4x4ahg/ihcZ8XdEYex+lDklL3RgVY5scJlTvowm5cyTg5BQ6nGN+w7DKB8AMdJuRlL+jtCRFStSA9zoVrGUue9brTIMlL6fj/K2bwSFJ8BqX9/deuutrR/11yIHHga8XHax8JogvQio8RP+413hmQP37Cs2CyXaZcSTYHwOOnHxbmqxfPCDH2xzQGgs/Sg0hGQoQ4AwI9f65eabb25hTGFWJN49eLp80m/CS7wqCiEihZB8NITFfHF/C49Kxi0UCgcJxxEXBl8OCILBSPO0MEiziEu2oyIaDPosJZhS5e7nuhQXo3AZIgrV8xCOqWf6Pc8MxUzxIiO+G48IA/jlL3+53ZNSlw/DE4AMIVhyA3JwZMIS7hcy5f/6IcZSO5PUq22Mq2cedIO5LPSlPuAR0F/GCBlEZGIsF4ExNgaMMW+bf1OjRcjH342dhNwexlryN6KL6BzkJFLkm0dF/8nzQjAkzpKzzA0yquqv/uFl8c5CZkrxC/WQz+QTGRsy3wP5sRsrcywLAXKbIxEKhULhIOI44mKlK75Oeb7sZS9rIZbXvOY1Mw1TQkWXXXZZ2+Gw7Jk8ITDi7+4zVn68h7Zxhw+3diJNDCAF3W/HZSR4coQcxkJZ8QL1SaWICyPtWQxEDIu8gmc961ktx8C9evIyVmhtt8XXthFkQH0WeUV7OcJAMuhJJ53UwnvGO/0Pxkrf6ntVYfsS9jw08pYWCUluK0LckRYyLGTK08LjEiBv3vWud71r6yPeRHOEhwuZy7bmRSox8zpKMkeO5LLM84gWCoXCQcBxxIXxtpKWaEs5UrA8DD5TRthqz+pO2EDI5zAcJshQIGQMCFe7d/J+PA3Pe97zGsni2el3PvHsMCZ9oS8GedEzdrYdyMTb3/72pWq0pH+8vw8CcuKJJzZPC9Kin4VG5D2RNT/7l9dPiEQohEza5svbohgd4nNQvV3ZsSYp/MUvfnHzViHUAdKClAlLXnjhhS2USqb0x8tf/vLWF5JrEWj5WT3J990QI9D3PDWPfvSjGxk8yuHNQqFwuHAccWEceE2QETkrlKaEwFnJuTmriELdzVlF2d48NPr7CUp80Z0njCLDaocTwkbhM5wMxY033thWsVzwyIuEyUBujlwZxjfvoR+RQCGB4RlPBwneR18Ip8U7Mg+p5iqkg+z4LuLhQ85Cangb1CtJcTVywLuQM4mMhyJrCqzp74O4Dd176DfvSnZ4TnhCLBLiOdEfcn70D9mTb0VuXM/j518eE6RFCIknxv2QFySPJ4p3EBnS13KBHvawhzXScli2ihcKhQIcR1ySeMrYIC5+5nWYl5wrXp5CbsuCUmekrOj9Ow+exwOijVlhUv4MK4Pn07vRXc9QUujJr+m9R4wgUuEdQqKSK4OwyJ9xDULCcMQzwBj3xCV1THo3PmOlPbupbbJN4G0SHjI+i75LDvDThwwreXJwHzlBaoJ4FD70oQ8d932GXB6SfyWJOytLKPCgHTlBBnhV1GMRikXSJDMH5Jis2eLNO4K8eG/yhbC8613vOi7fh5xnfpJtcpfziXxHWIhnEGnhcSH7hUKhcJhwHHGRxNeX9EdcKNQpT0gMPWOW4m2LrIZdk+/x5tj+KYGWgWTk4h3J/XkuklTIcNkOS7knP4JBtdoUWvDxnZy14jt2VfCIUOhWqMiH7zGanmV1KySUZ8kjcB8ERkE0Sb0x2LnnMAmZcfXpIS+EoXrJS15yYA9Z1EeMrm3PPABTspAzhjK2+pHBRVzkVzz+8Y9vxnWYVKvirXHR5733gffOuLmnXWC8LgcFIcb6AWlRW+gFL3hBy53qd16ZMxKVeUfsrrLNHonmidEfjlBARHqQSyTP9d///d/fvFq8nfrZGCA+vHyIzUFOYC4UCoUpzD0dOtstxwwWJcxTYgVptwdlOWtFzKghClbcPBMUOcPOG4K0IEqIExJBESML7m/ViTxQ7LYzW0WmyqcQg5oWjBuFjSzk+IB4gNyLkeBCv+2225qxsAuDwWQkud/dL2EKSclc876jNoznekdkRxv93z2OAoyLeiE+U6RF/xp7q3x9hhzqW9t7U6eFkR1LDpXTYZuvfA4ElgdB3ypId/rpp7dcmINYxp8skUe7sBAQXqXUuMlOPHPGe+b0a/MJ0UFyb7rpptaHU/cm98JAvKR9qX+ew0VKExQKhcJBxUziku2aP/zDPzy6i4GRYegRAitFsfRZOz4oVwr6jDPO2Ln99ttbkiLSIbcB4eD5sGJ0DwbQ7372Z3+25ZdYxQrFIC4ICe+GnRmUu9wSO4dcox1W+MI4CJJVqJ+taiWBug4RsqrVdkbTPYWEXMsIMAapKaOYHfLCS8Og8vZwzfP4HDbov5ScRxh5OX7qp36q1VbpD/frob94TZAWO2EY3hyVICzkxGLJplN5FnI9kMTktwC58n9jL5djVjXmbQOirw+0XWhIZWZhNqQk+WDkW1/pG94S4ViybOeaMfA77424I/Xk1H3NH0TOuPAEui5JzoGfy9NSKBQOM2YSFwrXyk/diKnVNo8Fo4RkzCv1nvwU1TwpZZ4NYR73QB58kA7K2O+Sw2IVmfoWVqu8Ooyhv/EEyDmxmmUAHBeQYl2pBsqL4/wi3/NMRlkoIqSFByVnMDEsEiRDsqyaPUfITFKkM10QrMNWByMJpLYhy62QhIx4IG8I5lRSrmt4DXwYZ/2FyOrf1FxBCqeex7h7HsIU8NjwcLmHvh4e7LmtQIbJIrKPTPM4Ce0A2eVV8j76jIyRPwRPSA3ZszWafOsL/UZ+vbsFhP4wd4SG5K4gLgjQQcv5KRQKhb1iJnGhLK0Ck7+AbCAQcXUzPlZ3FDGlvMiuopzK/IQnPKEZu9SISYioJwRW2kIMSIXvIRJZXfJ6IBxWo1a3DIDrcrji8JBGOzV4UhCbnGDs/u7Rw7vlWsaBIQLeFiEqhuKg7WqZhxyjICT4lre8pRld/TpMmB2DXWe8ZMZFWMQZVMZRTgsCyfiO7RjT/8YB8RQi6pGqvGThIIQ8QsKQPFVt9QHylpyvbK0nT8JmPCWAoCA3V111VfNyhfgj1uQX8RNqE2Z65Stf2YrRxbNVKBQKRxVzc1x4U3gZKEtJmlaFvBK2p1K8XP3xhCwDoRb3TniAgRpbPTJ8PB08IEMykh1NVqGMh7+7z1T1Xnkycl9SqXXqBOpcy1OQbczaMev6gwx9Z1Vvu7cQ2diJ2FOwJRepk1ckpIf08W4JdRjPlOwfHs4px4mBF4YahiERUMad4TZe2w5hLSFFCczCiv6fBF2ERQ4VAuLj50C4NH3e79bihXzb297W+hbZ4aHUJ+R2zHtVKBQKRwlzLTEDztMgR8SKkEuboeOp4G1BYqzQE1rot7rOAiKwyMFuCMtUWCY7fBYtroXQ5GylRa89CCv+vYLXSzhI7g+CsUw9HYaat0YojVGWt4HoJvQmL8mJx/KkXBeDjhzJnxnmzuhz93Iekfttc0jOu0nyRt4V5+M96is6C+XkbCU5WQhePz9ci/wPz3jKYaRkG3HmyeRhXHTOFAqFwmHGXOJiJZj8FQrUFmHhE0SFIraiTF4DF3/h4CDbzSWAyjNBXpaFsTfu5OP8889vuUd94jJyyTDbBcOw+3lYhTneBOEhRBEBFn4ib9vo5UIskDAeSKRdAq7coIR6kAt9kCJwwmlIPhLu/ZE2hEx4lIfKGAiXuSek0Jw8GAuEWeS9UCgUjhpmWgUKU8JhTpmVHMioyH154xvf2FaPlLgPA3XYcj8OM0IebL11cB+PwW6Rkvy25w49bgy40BHZeOELX9iSVfskbr8nU7wSQk28YcJEcoy2EckHQtjkA6m30icWC48hYfJ7Hve4x7V3yS4f7+39lQGQmCsRXbKuPJdXvOIVx8oO6LOzzjqrhZbkbBUKhULh9zGTuDAeclu4+XldrA6RFzuNEBpGL4fCWR0fxHobRxkIJ8JiV8syeS1DyLsQCpnKLWKI5SEhv0JDPXFh5O3skjMlL4Y8bfNWczKPuCMaQmDDQ0El0J5yyimNxMn7QcT0s7CSbd9yxISWbNFXp0a/IG3eW+gMcbHl3u98v1AoFArHYyZxkRRr5UhRM05c29zYSpMLDeUsHytmMfjdlPwvbAbGzq4eu8bsaNnLOVGMs1BG73Fzf+EhiaZ23PA0jB3WSb5ipJMIvY3hIbC7B+nQZ0JDSItQKi+LHWo8SxKKkX3bmEPkks/znve859gWaX2v3/SNrc/6gXdG/yQJt/JZCoVC4Y6YaSEoZatFRkkIwL9yXGx1tQuFQkZcKFyKetHE3MMOoQQeKX0UgrdtsOVWaMbOlanicotAAqowEW9Kf5ClvBceBoXV9AUC0x/SiJww0Ay9qse+u0jS9CZg/OTf2B7uk1pAgFx4dzk5PCg8T/08SDE6XktVooWJAHHhfQFzyPckJS96GGihUCgcVcwkLu973/t2Xvayl7UYvoRc4SLJgmLzhWkw0jkJ2Crd7pFt8kYho7wsl1xyyZ5CRMgHWci5OSkayHvjnXkmGOvhVmjQH3YgqemzrZVec4An0nLrrbfuvPWtb22VmuM18r6Im5L9l112WQuXDrf0S0hWHVoe0bCv5ckgNIjdFVdccQfyVygUCoU7Yq7HxWrTv/G+FOYjxjuJy8PwyKYhbPGJT3yi5WvsNkQk10keBy+DHJWEReya4WGQ0G2nzBgxsotIvpSjHxCXbQVCIY8Fgeedkjzbj+WJJ57YiijKa0m15yGQGQm2Y4REaC1VnRG5Ii2FQqEwHzOJSwywfxP2GDNEFK6V5lRy5lGDkJrtrPpFGMCqextgLBlfXhDekL3ktRjvHGapkGDyWxAXOVEMPW/TsEYJA2+bsARWOVT6Z5t2o5H1nMElJ0U/KeGvXguQce9rNxCPkXcRPoW8R04+9y+PjFOxQ4L0iZ/JhhCZSs7uweu0Tf1QKBQK24qFsyCFiiQkDleVFLCEXTshKOmjULBtHuQ4WGVLNmW4GWfejU2DIVWrRe2R3dRs6YG48LoYb2RWoiqD7F9nXKkNM3xnsmIbMEMuIdd3t8XLEE+KcCiSgmxef/31LeTnvSDbvuV0IRuScOXp9ISDh02oEHlDfuyQQnJ4ppA8ZzPpH6RPjRcem232OhUKhcK2YWHiYofI61//+vY57gb//yGLYvTqTlDkhe0Eo4q0SJjtS8zvBshZdpJJNHVfngn3lbtBJpC2eHUYd8m3DL4idduY15LcH9v9nR/UQ/sVXBTe8uE5GnpIkB8kDil8znOe0+aMLd7nnHNOS75FZnlnVCg2VxA4RKhQKBQKi2PP+04ZJspanYpU/ixsL3hBpk56XhS8LTldG4HhWUBY7JJBVsgBmehDUcJnTjWWzNuf17MtQDokUzs7SMJskHCfHT8OBpXXM3XEhL616+jqq69uBy7qC9uf7Sw6++yz27Zn4SU5MfoPuSsUCoXCcphJXLi4H/GIRzQjNJVgKubPhW63kUJ085C8Ge50uzWs1hm6rEYXLW3uHgyDrbxWtoyG1b+ieWOnQ3uG6xEsYQDbWD3PKponYFZ+jgRlfSD3gafA+25rrZEpCHfwtPj05+ksCx4CYUEERBhEPzLAtsPrfzvQhiEiv/edk046qdX82bby9WRR+AZpkdNCLiGhrbvd7W5t15R/1Vfpdw4hgd7ZFml5YMr/y2UhZ2SdfDrPyYGS+gF5U3yuUCgUCrvDTOsrDi+Oz1DL1xjmr1hlM+hWlBT6Iu5/hINSp+iFFpyMy9A5mM+KNARoXqIvg2BrKqPANS83QZiKa969/Ny3B7mRd6H4lzwDZMWzvJ+chVnbla2e5fggPt/wDd/QCN1BWi0LgXhvu2MYaIZ6txDmkVDKiJML/arvjaEibMJEPXEhM3I4hEXsnpEXs03Qdrugbr755tY/iDQkNMTD8shHPrIRjmE+DiLrzK7PfOYzjZjIjZHA7p49eKQQmpw9tE1b4wuFQuGg4TjiEq9K/lUsy0Fytq7KTVBnogcFLXnR7gtEQNgAgZmC+1qhuu+VV17ZVrcMhN8784VhO++8847lQIztskjbeE2uu+66VrI+5yRZCd9+++07F110UbsXwxMIY7z2ta9tBIQBch9bduVpKN/OEzCWs+Dztre9befd735389rwGggZHCTignAhbUIYvAN72dYeAiLUAfpGNVlkBYkZ7iIKmVTrBbHZFk9VxhZpQTrkbkW2yAdP0kMe8pCdk08+ue3+GX4XeLHUZ1GnBbmdtUsrNWGqpEChUCjsDcdZESERYYSsOnlExOh5NBATuQm9cect8ffPfvazzTjNqxBLsXOnv/jFL26GVMIikmLVqraInRi33HJLCxshScNiXpBD7nhsGEwE4oQTTmjJkkgJMvTOd76zrex5jHhutN/9vZd7Spa0LVW7GS6kKSfy9uDVcY1+sI34IJGVHowqrwDS0p8TtAx4VxBB/dx7wxBVnjcE1vjn/jlsEBF1OrKw3DZtlyeLzmhCWpDakBHyra1CpDwtY2Ed78tr6JBFRBlhmyIt3pksO4tJeM3Ou0KhUCjsHscRF6QFGbDrAZALpELM/4Ybbmgr5h4MIe+JUBGjNa8uiL9zmwvvCDHxcqjnwb1u6ynvjo+wxlgV0oDh0CbP1yZbaxkHyZVf+MIXGhlBqoREkA2ERYl2q2i5FhIkXeM5yJLQkRBQT1yQI65/IYSEiQ4qcUlIbS9JufqZ8dVPfWl+xecQO56HHvJYeOmE/3xnm87d4SlEZo2tmjYh6iCnhUeJZ83PfSIuWUcCkV73eP/7399Cb2O1jRAWxDnbpx/+8Iffoe8KhUKhsDyOIy4MG6KCuPg5RITRFlYZvcFXfEXzbjDq85Ry3OVWqxS7la0cE89CIBAlhISnA3EY273h+4iOaxAYz0VGeAMYE8bCltYkicqXQUCQMj/b0cEgeaa6GiE6SEwP99cm3hjvv03egkWhv/U1Eoe87BbGQV6PSrGScI0BIuj+xn6Yt0IOVIRFEF2/baSF982WZ8SDvMXbQoacnSSsJU8qICs5wsA88H1kJXI6hDAnr6EQk/vwLPpsUz8UCoXCQcVxxIXRV82U94JC7/MVpqp6Ig52XFhV2mWyLHK4nvyYFDObBZ4dq+RUMg0YBeEM90kSJYOE3Cicp/y8pEhGdlaeRYwYY682CQLEoO3lTJ9NAcFAWHy8x26B6DlEENEzRjxQPBYMuv71/x7CR7wtEluHXrpNoN8Rh4wKDzl3SNvzN8RUaEhOi7yn/nuK6iEtb37zmxtpmRVuI3vm0VOe8pRjxK1QKBQK+4fjLHhCKa985SubMfrABz7QtnYiJI973OPaKnJIYKwueU78bSq0s5+IF2Fe2EP4imeG4Vy2xgyiI4zASAllydUQwhoa6G0HA8tDIJyx24Jz8Zyo8mqsGWYhOOEhuSGe0W+vjgwpsIbUboOnShuRD+MqJ0VuS0iLNgoR2vEjnNNXsUWS5XBJPve+QkWz+hFhQXqEmvTZboh8oVAoFGbjOOLCKNn27LTbeF7kKEjIpIwp5iFx8R0GjRdjHeXbc5bMvHwaBjOelZwbMw8MlRCIHUQOIUTEJJYKn3lvZIknynXa0fcFjwwvEKKQFTmPFU+P7yxS42Y/oQ3CIkjL8HDAZcBLhZjyHBhfxtuWZztqeKWGCdlCIjxw/uVJ23RJf4QV4bTVmQcNGRUWDGmRMItk2DknB6WvMWO89Z3aNyF/w35UmA7ZQY7NFcnmiBuv0xRp4wnTf+SCfMiZ8Sx5XZJ3ebZ4uYblBxBxnrNZ3j9z1Xtkp90QcsyyZZ330fP6EG/q/YD5P2uXYA9kVtuEz8C7WDTsNi8M0XQv7dQXlRt0sEAv0BVk3FjSv+TaXGFjer1gXpFL1095M11PpiwGpgpAAv3tQ/dadNFffYg2Z+5pj/D3rHsFZFDbhnmcFjz9OW2Lwn14wdlNfZEdmoXFcYeYCWPPyBpsq1D1K3Ss/xvAvgZIwjyuX9cBcZ7JuMzz7rhGu1zPY7KIgBIoSl3NDYKVXBg/m4AMhvwZOTGUMiIXmHAUtwThGHO/o3wZtXUTF6RF/o4J5/m7BXnQ1yGBdicx/iY/ZDs76Gs5Sz6b9jYkTIgYSBwW5qG0EJnIEJIhPMQ75P++g3y6Dukwxow7Ek8uQloDhh3xQep5nRA2ybizzuvSJoqcJ9OWfsnwxsl93Q/pEHZ1thFSYd6l2KJref6GdWJ6+L46O2Pnhnl3JInXSRu8v0VKTwoQNd5GfeG95hEXJMx9vYOdZQnhIrvIoJwyIdxlCSyyyctFzuQc6Vdh4MJ2g75EHCSx25GJBJs35ARRQO4taoTfE9b3HeN82223HTsXbAj6x/xgj8aKWGa+W2B4rvkoJ09B0p64CHFblLr20Y9+dGvTrLpK5ol34V1OhfCAF/rbv/3blyIe5q4+kV/nHcwPeqOwHCaTPaxKsxOH8soBfQxzQCEllLCu+hyeIyxlZTkLjK22u17CJa8JgzQLEX6TzM88CnIVGJUILOX8mte8pv3/tNNOO/ZdxIghUGAsQPKs8tWJWfdxCBS/83bGDjvcC+R68F4Mq++GxJKHbTivyvhRNJThNddc0whckOTZCy64oI1ZDCIFqjbQq1/96ibbl19+eSMmiAsSo2ZNfx8EwU4rRG3KwzGEsaBcL7nkkkaItTHQp8YLCaAQFfnzXLJGfj3f+8zyHtq+jTCfeuqpdxgHxFp+2Atf+MIm4zlDqSeZdli94Q1vaM+wmrz//e8/8330GVKnRpLdeTE85h9SiPgxDssSF3rGTkNESL8iL8ahsN1gmG3uMIfIRe+ltCA0pubNs571rDaedHQ2hZinqVo9Brr83HPPbfPX/OiRFAKh3WuvvbbNJfdHoHuvHzL8pje9qS1CtU0qAB0wBYsL95PMP/QGed5jH/vYpiMWhUUf+4EIee8zzzyziMsucBzboKyyq4iCM+CSMq2cDDaDFTcyUEZYMOViS3Jf8G0WfM8KMm54ShQhQJSEJHLqcIyPthBWqy5/p5yj0JEDdTQIFaFArpCIuBQpPZPDChoZI4CKqPnZu/o9YoPFu46y9y4UetpqwvWrdauGoRL1HBOrXwlon3avO88ju7e0d7chokCCrXcQPtPXCNFYvR5jZoWjbzZNXMiCHCcKQp5Wv93Z6gjROP/885vy824pjMhgUyiML7l71ate1Yw9eUBSjb1zjKwO1Q5iTMlNjPI84uI5tqV7DgLEC0eJM/DagZTYxUZ5v+xlL9t5/vOff4w49AXsyLX2I8kIPCWM1FhpmguOLhDizDj4jrnhHCUrvZDwFOEbtrH/zIO+dcAqskUXUML6B+k3bxEYOXOLhIwYPWROuFU73cOcWiQ0PGy/6/Md45NP0P/d/IzncOx7uV4/us71GY9833Xr8jpvM8g3b2KqqTPqPNc5y4z3Qo6Z/rOwojf6wqf0J69hvwA0H5EghJ/HV3i2n3eehWCwT2SOHZmlc41lv0idBXORl921FhKIEMJiAYeo8+jMIy6RK+1TY8z7s39pw6LQVvfJIimyPianQa6NjA/7oZf3XJtnuOc25CiO4TjiQlFQnHZdUCCEg3KnDA0SxcgYIig6nsAQEsrJACITVqpT0AmUtdofiAq3twq6OsrPVr5cZ3Fzc9PZBUIRGyAC8vjHP76REsSBsvR8jJjACwtY0bpH8hU8E9HRZqs4hhcJyzlJrjFJTLKeuPQrYW0mqIiOPuGu5FnokUHvlWPyftat0Kw2jJnPbj09+t942s7LqEpstVrRx8PEaO+p/xRt23StkuS0vPe9722KIkRLG7WNcY38UrLkI7lAUaxRJmQvYQ5u5ewScr1VGpnnZl50fJEgBILyJWtIiT4Tks2uOLKtn8lXb+x7EmG+kUM7t1xP5ilX85dMW0hk3FN+ABnwfsKc+4mEsZApCxzVhs0dRskiQn8uWi1Y+3m8zFPEzn30waLkG4FDmvQx2Ue0s8vLeNEDUcTaxtgZS4szMqEfjQ0ZR3DpBe+UU9UtYPR9rk0JBf83HuSBPjmKBEYfGS/hTDJGli1k9C3vpjlIL9DZ7MZUeoHfC5XyhAQ5A8xcJiNkKjJBzs1dOt18ptf9bpYdCkJgZsHCgK0xzx/84Ac3HcIOkFEL70XOfdMe8mjhQI9KHwhZWES29S059V3zwrvpS8+mpy2yyWrqUxmDgLxqu3Ggu3zXM+kiOkNfxsvlOvdjU/2MqA2rhm8LGnEJczPhxb8JlwmIQHgBCjwF3bw8ZetnguJv/tWhBngeccGw7d4wGJ5jWypQfFbryAmDSZFTiDqVIqYoknSoc3UoFs442fXB2Pi99rkHJZKzirQLmTGoYvyImQH1HIPOlZ2CdwTVtT0808TzfcJLSCRVbRuGRzUMt4wvA33BKPrXiofSsJoZW/kyDPrMmGwqDyGrF+9OQbzxjW9ssoNkaZOVUlyyJjzPW0ABUYxDA5vcDXJl4keOdgvKi7KguK1CyRLSEjlFiBEriwVJjFNbqY0B5UKBmhdkMwnjUVQx0N7JNeZpFhn7CYbGfGO8GRzeS/1mZcmgLBMiinLvV3zLwPv5PtLKk2vhY/x5ap3OnWraYC4jScYD4SG7rmcAjblx9m6Ii/aQ/UsvvbTpJX/jBSJrDADSwgPHmPTk6CghXk5yhjwiK8Ko5JgtIRP6jq5lO8jomK0gnzm0NfBdC4/o4b5Mh/8jmkg5nexZi3rnFoEEXPYO+ScjZIhuXWZRmsWUD3mki5CxRQm96yxIVJW3gCaXPvqZviDbFjoWPDyvbHjyUuNt0U8WXt5Hu5FLkRULGjYxeaDa5/8SqX1vq4kLEDydkxg+wy9p0apOmMDkJlQE8bnPfW57QZ1k4hoQ//ZeiikQSlVJdRKSwG0GVkQUOeWdFbtB8Tsdzfh4dpQZNmjw3I+ionQIBAMjFOTnHt7F8yhUBM1AMRpWBVyPswgXxccLYxC1YV5+zSbBeGPc6dfdwviSB2dBmQDZiTOEiYEQCF1s0tOSGLfEUgYppI28GL8zzjijKUOERUhm7PtjQFooQ//udYeUecI4J9GQoh32mbZSQrMUIsUtlMJjQG4pJQnICBiFZUt25DkhTO9uvpinY++/WyC3vKB5FpLLM4tEJO9pUQ+EPjZvHR9CfhGIZcBLLJ+MrFrkIFMxGBQ00sJzBnSZdukz+Rieq73mDnm3oBEm7cEg6muLOIQGSSFPjAAZMaYMw1EkLoyrBQH5oqvJIPKShYw+pTuNSzAmF/Q4b0bvKWZIeRsQcP1LX/fhWX3v97x9ZMD3kaj9gGeZk3mWxQJSTA7I0CILgZyjp40IgTlqs8Cimyb0LTnlqdG/3s1ix4eMk1X9RScgLeYRnUymzQX2MZEN8xVpFFkRRdG3dAVyxvb73UHAMY8L1hq3kY72IkhEzgXihhIOsOrMThPsU0csU9/EvSkzuxmQoyc96Unt9zqTB6Q/C8e1Bse1nqmDI+wGx6qV0kQqEC/3ZQyGJ0ODtrqP7yBYJhIBcu085eoak4MxT5G7bYSxkjHvsx81Z/QJFq9v9dmYcaegkE4TaFNbn608xNW9N4OXHU+QLf12ACANMHwPBp0s5qTrhMLINmVo5cjo7bXyrbnFoENCi0O5WyTJ13hY9TGY+pxCotQoWHPWfIhH0FxC7iUBer4+2k/ikhUdZLUmN4hxj1dp1i6rHuRIbk+2vXo35GwRGHPPtpo3VhYk2e0lCZuHRRgoxMUixN/Mk+wcSb8bb98d7lwJGAUeFvpQ3+pPBoXRjEFbZC6YU0JQ5G4vO//WCe/F42RBOwtD+R7+O4WEPftK5oi6BRmyyKNnwZn70MX0Ov3DfvAi8PTtF3Hp38HYkkfeHbo2ZRTmgc1wncVDzshbNpzY55x5Zwf9kmFkiLwjImw42UOOJA0jiX1leH2SavIImP+7xqLT3DOHkB05eNuOYx6XkJFMuBhrLMyLe2HKnatPp8eYTW1fm0IUnfsvksSpXWMH02lnXGZ90bApICc+u0kcDbvddpjcFHTyA3YDyhjJowSs/ClVK4x+GzyYjFZUEksZy02ROeFCq7GsfE0+CoacMYCUWg557JN0e5Bz7n4kLHHf1PBhoORkTZ1Wvgz6RLgpUNLGzvMY/LEVnfmj78kz5WN83JfyTlw642GeuI854vpVnbeVXANhW6SK/DAwPKAhfHSI8dHHSI52IVj6Pvk92eHkb8skLiIfiJm+885WqJQzPeU+iB1Z9nuLI4RW/hbvDm8MQumZlL7QFz037Psk+guJkRXypf+FkRAgO8KyE3MRfZGaVPpu3gG12wJ9O29ceAiMb5KqexJHj+jHqfIQ+oScGiPzlX1xH9cjk4hLbBDEPsRG+N5+H63hHbwP0i85n37gbePF73c3IQ70UfJezEFkBTkg5/Sqe/Hq7UWXkFPznOyaZ+YVuQv51V8Ikt9rqz6kVxJepj8Qbb/TLrl2yA/db34eGOKiExl0jafYhIWsHgiBgRCP0xmUvwFLYTWGwt9DRjZdbOyoIyvvvRxPQBmn4BzjSJEMtygyMgyhXKUcHrhuUI6phnvrrbc2hRKQxbhRGXGGZhYoPxMYUSH3VkSUp1WLYnKL1ABaBOaXeUapMLAUTZIWwRwT4rJKooh5N8dIu+uFQxnZbKmmcLwHZWkMx8IV/q5fEl7aD/T1criqrXg9g/HXn/ovIJu8t0gmpYowWgzpE0Si98wgGfppUZD59Kf2yFmipLXP7+gyz6PEGUHP8jtGkNcDGDz9rS1jY65P9Z1+Jy8xmu7lvvQkIjPm8R2D55k72rHucgm7BV0/lXuVXSjeJSGNJJLmRHWybe4mh2tYRsP15J78yJfh4WBjXGc+54T6dYFORbbMM7mRSEdCK9rYb9JAyHl8cy4cUuEa7zm2q2e30M/uPbZYTDK+eaadyAq59yHT0TvGyLslr9O/ZHa/dN2qcUxqki+SrGN5AuJllGncnyZZdhldffXVLa5uwhJM36tD5A4+kFErx37L3TCJjBxwxatxsylBN/HUbFD7YZjPQxYpOAqDgaT4+mKBQySxkMERVnK8Bex3NWjuWCsgYS3KTT8znImhUyiSSy+++OIWZnnBC17QVnVDmIsWELxJCIu+kNvD08GQWo2leF0P4dgQUkRjP8Ag0QH0BW8LMilUJTSVkgIBd7UxM17GhcE3Nq5HtnriguQklr8Mspont1n5IuIIktV6ji2xgvaMeJNBPyLp2mRcxgwDedCvxqAPOfqd65epFu07xnmvJQvWjTEDnArq5h55QDrsHKUfzD2LXXIvFMiTIsxy0UUX3YGEJPfwmc98Zhsf9YEkpZId9si8TuLoOkAmeDRf/OIXNzLAK0H3qScz1H3IM/nvz4VDenZ73MpuoF+0K1u3+xCTfB2fJED71zwwz8jtsMDsNuOYxwUoQ+4nKxWTXrw/L02YuHStKiSzWaX42crDqptS3oYD9Y4qKAuGkMLYy4GKY0Slh/i21YYQCha/ie3elJgVtR1pVmQpDKUdDBTFRllIwpZrYZWkdovvjeX+kHXhAu8iv2GZglLLwErejjReCG2zzR+B8H9jpn3GTzsY/VnzKatbREQejjCND2PBo6HuzNBbk9o+w9LlY3CtsCNjQQFmjJNwq48ZasTJIkb/MfiUIf3hd8gIRa8KcJLr/WxFrR3uo42M9zA5ftE6MkFWiyk6SY8ZczoMWdKXjGJIBd3FsybMQ3kLUcWFbmeRZ6vT0xOnHNWAeCFHdJ/+0QfGAenVV96LzCGhjJnNCMZ4aGwXLVp4EKDf9YFcDqFqMqCOEkNusYuU28yBsKdo4ZhBj/c+5RiEGoX3bBLQp3I5hFwWyS2ZBePLYNMPPUElOznmRFs807OT58l7izylxlC8hSDvhw1NmF6faGufm7kK5KiezKGEh72jfqZrjA0C6Rpy7HrvTf8873nPazJq3GzEGQOCL9/R/JC0bi6vuxp8j+P8dBJ9rPAoci+BgaXzsUyDRuFgwl4+7mxFtDC5Ok9kMzAWFLFia8NqrPuFGB5ykJXrOklLdnQwpkgzY8TDkBUCg0lBaiclSYatnpEahoWX0PcpwSHItFUgRdZvtdxvUBqIC+KXYo8MPsVCKSYxGCkQCopLPrkV5lfyrfxMwVOy3tup1gwD8ipkY6FhVdXPSX2kf1LfaBa0DwnSNwxIxjnhErlNFLjVKLmjAPUdWfQ7/9dmix1k0HOtrhEyZMZ1SbinRIftcb3PouQF8SCTDI6xp7B9P7ktXPrxJpOJFDMjP/qKh8W8QSaTyGus+jBjvkv2jBVihsQgMzk+gTL3XsJcwpeus/qlJw/zbiPvRq6QfmRFmQpy7ff6khwhiv6PdEhwnmUvIvPkh76h35AHcz9b7/dC/IwlGTDf+mrwmU/CxPSBUh/IrZ99RztEGshAipfSiYAYzPLsgndCsJeRBe+YkJuP72dXHJA3bSavdAqZ00Z6AtEg//IQU88KkrhubGyxNj45m20M9ApdZXGVTS1bQ1wwRyuVFAoigCY/UmKADIqBk6yo8Sm9nJoHhd8HQUgF1lW7Cq3qGItUdZ06qGy3yHlPvCxW9wzEOpUwI5pzooRErGR5TrxnqhUj0ZQhDwzZ7ckb4+WT1RQ5TsKae1ud+J1kzUWrP+8W5hLiAvJz5LQgWvqTAdc+Csg8TKIqBUVZ8UxkrvlbkncRC94B8WyLDQrI+/X5MxAPh8RS3x3mlYD5btXoHvrGylKfuheyEQPFcFDCyevoE4kTevF/7xbyke9O7dbpgYAgysYtlbRnwTW8GmSAoUE+rBLJgedR/HHtexfEghLW14iVXChK24LN73OIaE9c4g3wNytx8pddTL5PL8YwJJ+or0FyFEA+yY73zonqqefDZiCuwkQWyL2HIOELc6BPICfnPFk5A8kHKSabYzqIjJtDCT0Ow3b+hjgz6PkE7ofgkhMya2zJr7FLSMv/kZmUGeDhXQbuTQeQVcRhkUNMc26aZyEl5K2v1aQd7oc05ow6BC+JzkkMjmfJ9xAX89ScTrFSCyUEeyyMTNZDJqMLNok7HDBkwL1U7y7vS//qQBM9iYCUwrrOKTpIMMEIOAVK0S26JXQ34C0QYvDZz+JLAQUjr4U7kUFZ98qRErSSePnLX96MfU53hdQtQawRxOzKGSK5D9yc3oFxk29i8vq/7YVWTlOJh/uFbFcUI0cELQ56ohkPRH9wm/6mwM8666zWRv9HsCJT3o0iEx6yQ4DCQlDGdiTJp5E/4L09Z3gYJnL0+te//lhVUYqQZwtRpLTjgaXg0k7ehmE1ZaAXElNfFowV5UiJGlt9Ng8U+4UXXtjahxDqV33FWNJpvCreiYzoO0TDvRnbbMGWg4Egk6FhDkO2lhs7YJjdzz2ECfR5CIr/62sy2dcdOexgKI0d8svjaZVunvm9lAIelBS2DMiJ/s9RKv7tgWAjO1b9xpXsTxFBRt24WmiN5XmRVWPLmzgE/ZAiqO7v+xLMjTkiYE7QNa5JCY15HpYhvHs81vTaIoVMU/X7vPPOa/l3dIQ+6fuQfCHtoib6iMfLnPR/Os/8CflKwrrreWJSYZq8s1fqvgyROmYWkDkgc5O4A+MIk5wiI8m8D5k5zO7PvQCbpgBzDMEqiEsEkKDZWbMK0gIEluuU8HuPda4e9Z3VrcPZuDWt7rPFMiSaq9/vFHWySh7CBKcYJYyaxOSXIUthRcqUFyRyvUrEvW0eUXr9WS1gPmlvP6/yHddSovn+sDYGpRjlNFUcixcAOUMKxq6hFPuEUcaf58M4MMJZHZMF/5INimxM9uLi3k0pAW0wvlGUi8yf9Klig77nHUJY9V3OGNKHDJLQjmcgfd5LW5EM/ehdh0avX2Vb4ZIhSP2pXnY8I+dg7cdW+oOC1OnSJ/rdvMsWdWMzDHOAsUXynvrUp7a/D09b9l1jZFyRTvedmqdIqoUIvUhGh+STXJEF4z9ECFSe7z0YfvLAA2os483J85fdkJIkZsTFnFlk0Z/5rx2ITubgcP7rF23Wz/rT/TkW4rHMs8i2TQ289Cn6SO6NEzI+BkQlhy0vk4C+KiztKklyXmE2KDKTxIparHcVYHx4H7jEswVvUZjQ3KKI1azt0yYZwyUu7ed1CawJkri43SqptRGDYhLLrdI2rn3uaP0stNDDBDeJeSKEuay6TWbvTo4ZZhM91WrXaWASs14U3nuWolzkfslRmQLlNlT2s1aFZGIVh2oyED7LIEaBsZlCjgwZ86zNC2XlGAL9k51gU5g3VocZ2XmVfI55IHOMrgXEFFJ5dh4YaZ8pIJSL1jLK2Xo+++mJTSX4ZTGPvGch4t6z+iALCl5sISK6lAcHcUmCPa8VMhOkxMS2oGI8K0JKrBPSbP/cbzDiXPhi88vmtfAuCDvkYEEhgTFYGVAYfYLmqpGD+3isbIXsT3hOuXwJj1ZNVgj+Lkw2PA2b4kx+1pOf/OS2cs/kM3GtuAuFRYDMIGg5A6ZQOKhIUrGogDQGC79UKqYf5fpJvp9X/2qTKOJygIGs8LakjPwy4B4855xzmnC+5S1vGY1rAgEm5EP37SrhvTD/K664omX89yX8tUO4Rw2ZFJ4T+x4miyGMyJkjJYS5Eg4oFJYFuZF7YS5YzQ7zggqFgwQLUJ7nZz3rWe1IDkUjLYItCnmeHY8iYrDNkZUiLgcUqSlh21sOxlwGOfiLe3Yss52HRYKhBC7eo3UZfbFp2x7FYIWJsg0xmfVyWuSjCO+kJslUhntc0H0GfqGwLMi+UCmPXTx+hcJBRXK1hPEQcqGz5IPl6I1tr4S/duISVz6G1xscneSz6A6lFErrtxonBj22/VD4wfVjz+zLMafw1SLXbhJyOSStjp0jtAhSIAp4LHpwixNoxcKSE7Jq5DwQu4YcWoeQIS3GQGyX90SOip04trD6vQJjdrr4u7BSxkt75SDI/peNX6SlsBeY9/05SoXCYUCfw3PQsBHiwkBJCk1Jbshp0zLBxZDnsT05I3I7+oPzkpzHaGGTPQmyX1/IoT8U0nO4xIRN+sQjxjAFyQLG0QAzoNzFu9niuZ/wLnJndlNsTtvFNF/ykpccq2USZAsrT4taC+tg3clpyXkgclZSCMk4kglbVs8+++zmdfHuxsY4C2MZD/cwxiaj9tvxof2LJPQVCoVC4eBg7cSFh4RR+of/8B+2QmIBdxVD44hthmdeApxdJEqbK/seIB9IyAtf+MK2TbPfDSEJVRlySZxBihs997nPPc7A2csu76Mvf8xgchefcsopbaW/6eMNeBcWKd0+Bm3n7kZS9GNOFQXk0TjIC1mXZymnmTqbx3kmydlBQiSK2T0kEdd4KfVvXFR79B7yXYyH2gvyXeTASNz1++G24kKhUCgcfKyVuDC2ihK94hWvaLtBeDBsZ7VlmAdAIiayIfEydReGiMeGgWPEGG/GzfVW4ZJVle3mIbFrhPGVA6IYnJAID4W9/sIrrvdMbclhYO4vXGFrLVKgfUIPVvNyL7yDnI/sp98EvLN3skV4Nx4Xni4eDn3Tl7jX35K1kIBlCyvtFp4vl0VOi3HQNmOAdNjRJFFM8SmJYnYYKWfvOuQm52lJ5JX3ojgT4tKf27GNSFiM19CuMGTamPLmSY6TS+E9hmFT19u6PqsSc049hjHi6dmIIs9jDgbsnyNvKJ7QnCi7CHxP23LqdI4nWDbBL0c7uFeqdaYWzKa9nIXFQUbNTf9alNh2a4ttTukeykVONTYvxnLWUh9m3mG+nkd+6MWcAt7bEc8wj+gYemKRHWLao13DKujeZZm6VuYIfdfr3JzKvM5SE4cBayUulBJhtlpGGrj/bcmlpBxWpniYMyBygN/YXvecF8Jwmww8NQwbhc97IOdDoTL3VuXQfeRz+KSSoPLo/q96aghAf86Ee8qjUP0RKcpBbaotIlhRzpsCQ42gef9Fz3JJ0SKTWP8hiz0YKCRN6EVxrVXv2U+dFsRRTosxyBlYlAnDzYD3O6fsIjIGCeH5G2ViXCkpnrNVV77dK7wf0oys5YRo/+qLhEoVOFOl2P97UsETiIAj/1OQaJ3cnuEYenYqOpsrtveaI8Y7ECK94YYb2s+SsxX3m4UQIe/jntkBxijwnJpD5uYiuWv6hUwbb0cJGNt++zv5rK3I2w+kmF79xCc+0YgCXUtvqsBMPi1Icio6nUR+LAwtSnjjzYUh6C06wWYC82OYIJ28xBxRYU7ZMWmR2usEbaBzEBDngbnX8ITqHq7TNjZFekPvnTbP2Il5ydqZIxZc5nCf3pCaQGzYOnIJDwvWSlxCOihPLBWJEAagYAkspYWdG9ipssIhP4QJ4Uk+hmJvBl64wCqWcXcdhu55JhPjpuQzssRgmEz+RWD8PqWeeWooXJOFAZAoSnDdK8mqm0jQzeS0Qmd8ljk917voT31t8g3rvjA0irSlXPYqkbOHKBknrwoZJjzEUCGOFJyfkVwrJEQLKR1Tar7LS7aKwyX3G+TQ+Alb8uBps/dFLNXT0S8INLkehiQpvoQ7c9xGToFl9H2XEkQeHv/4x7c+TLVYH54UiluFYSXMJWALCfbERblw29ATgpxHXJBGRAqpFI5FOIxbDlQUdhRepaDnrSjNWWFABixGgmFjeMire9aOnu0GeaB/lVdwdEROAScTcvLIes4rOvXUU9v/XUP3X3XVVU0nuIdxj7xEzyEuOdQwi0x6OHoxRwzwzJorvLXmSU9c6AnHOsTjzCbMIi70jnu99rWvbfMuZxdpswWw+ZNdOFM2QdssyhTStED3rt7P780LKQjO/EPwi5gvho1thzZwtqka9BxiRRFPFUILEiZCblIFlHIn1O5nIvSuwZy3QlBT7nyecCBUCAsjw5iYDAiOthLURQ7GWgVC2qworEqXQSoemyhD45+zbiiUdbB+z6fcLr300rZS7+vQIFDylMiDlVFKt2dX2Bh4Kew4WrbS6iZgxfWmN72prUa9F0+CM1zIsXoKFKv+QB6e//znNwU/hLnDU4JUkFUeQIQdKUH83V+JcnMi42neMBxOkEbEEQGytJsaQD0QJvPDWFlMZPcNAmRB4BkWBAjWvLARYsrbY0FhrvI4GXfvhMAyVoxRYXuBPCCeSAvPqFxDsmjs5CMy2uTQQpX8GmdeDYsTxp0sIxMIasIn9EVk9aMf/eixRVaIDRlBKCT2v/Od72z60dzSln4zxhDaMG9HJluD6Fu4kt9sHkGwzDnvZdFrrk0RF7ZHmxAgbWKvLA61zXuRe4uYlNUvzMfGiEu2Lodk+Nnvwk6nwjH+jrSE+eaT7cq5T04lpURtG+auZBzmbWfOHndwLYVPkWLelK/cF6vhRctG7ydMAArcZOqLsi2CnGxrsg6r+OZ4AkZ01VvjeBiQFXlI3sNY56RXhgppoXSyupl3CilXbVb1ixTJo0x5BazuKQyKiEtZGGLVJf8pXu+FYHgOsuUjrEnmKDOEmcHnEp9aCVLoCA1CoP36iIfw1a9+dQu75fRiyp8rnGH4+Mc/3lZ8+j4HIur3YXJ3DlEchhKnQJYoZeOITD360Y9ufXnZZZc1MkNRU8oI8zylnJO+EVDhYvfjJXrlK1/Z+s3cm0VcvBdD4Fpja6zpAytZ/SlEEfl2L+NgbjM8/s4w5WBU7eWJMjb6CKGUU0cHuJbBy7lYPFc+OUZiG8olbAqMsw+ywWPIq0KvkFlG/lWvelVbtOTcmxzmmQ/QRfLVjBd5pPcQHoes5oToXJuDOJElxN+459T4Mfnu4buLbG7IMRL3uc99mq4wvkiSOebZZAYJm/Iouj4bR9gj13o3+g/pJ0ds2rzq6vSCULnrLMDNUe9pwclj4xlZMNDz5kPC7ggkb2y/uFNCQtuNB8QRgBiSb3JO/hGqbZPprStAl4MDpxIQE2aYlaAIFFiMYpj3sgmblJQJRoERLPdz6qbYJiHsB9NEJSyOFI+xJWDIE+W7H4cs6he5NibnrPOFhqCstddkoYCHJ/n6PSWzSrafLc9WLsIBVv0UUF+nxRZmBJN3K9uhh2CMQxq9k7AeAy6EN2tykStjxFjxdpisVvKe62enn+qHVXqcyGGOaNB2CsxqNPVBUiwPMWYEp/J1csKxj3fSt8MdVP2hav5ODj3f7634pogJw+v5w9o+UzCnKLiQJ8nd5OiNb3xj+7t5OhaaHIN3FgbQNitqBoxS1yZzry9PMAbfQ5KEKSxczD/GJDlrQso5XE9fkEXkyjOEIPQL44fUeDbiSHF7N2QG2WYIyJo+jU5ANhk1ZPKo1g1KHge5YczJhTEk34y+ual/k++CACSHa6iPQnLIA3klP8l3Iu+9x5h8MdZKKBh/hFP/97koewFjTzfI9yILSDm9ZRGQmmHzdDuZkfogLcK1QkMWKeQ5pRzM5Xk2jQx6Ls+m/mHT9Kl7apfFGN3G6+ReCaP5iBxY4CHpxob8W8zwGiGFOdk8OYb6jzzTU2R627B1xCWHoE1N/pwUOk9YCH9yUXJq5iIIcYoXIMm8GOjNN9/cBpvBGxZm8x0TSKw/E8uEJJyU237E5t2P8BLcZUBxM8pYOWLVGy39Qoms8twefUnxpE6LVUYSTPvkS0ZPLJlHZIiMo+v0PTnwM6NJCczLn0iOB+JnB1NvBBFBE9Yqb5WriySJ6w+KjELoi5qRJ8rRZxbIWnaUUazaTvnwNJBZXhi5Sr3M6WfEIkSt39nQAwFisBctBMn48HYx3BRidvdpYyoXI2CLLBqQBUc0MIBk1pxjJPTXIocukimkRR6Bd/BcY4msmjfup529sWFkKXxzipKmyM3f3jsD5jA5AW2iF6xMyTSSpD/1rfFYlLgwLu67iNHaFug34zD0zJJBi0U6UF8aP8Y+ZRfA7+hSc5WMBsNFWJJh3Ys8MtBkVl+Zn72323PJi/5jlI2xa/eLuMSbFiDDyY30XPPYwnbWmOszi4EcWqitdLA5a66wVfp0XgqD9ydrnk9mfYcMmh/uKW+NfuVFsRDNXORlRcZz4CxCaD4Iu/HO0DtsAx2JxOdQYO9GF5sL5XGZg2SPTxENv8fihUxmrQoxUEbNpLnHPe7RhGRR97fBS9IkI8mQGHxKDXngIiSEjENA+CheW7njcXEPbvTs0tgUCC/3Ldbdn55MGCkQrsZ+cu43UlxOwTsr4j7MZXJh9owfg0NZjUH/8qycdtppjbCYhCZ6n8Q3Cya3ye7+feFDYPDkflghmqyrAnlNeGEvIIMIKOVDvpOcyOAyqBJzkaLMIX0k9KIPGF8u96k+M0cos7Ek6DGk+mYWCbxJ5J2CpViRJQZl1gnTAQWfLc/uRQHzgDAWVr3zEoXJOYPnerloZAouuuiipox5SMgeomte0wuIDmPnnb0LwmW+88DwrI5BjSCeIZ4l+USSy8mWMRH6WzTBkqG/9tpr2/f2mmu0LtAT3tGOnB4JqVvU0TFToXREZp4RNEfe8IY3HAvrJ7+NHuExQz4jv/QCIy1MitTw5ubAwFXA4kA4lh5JPSzvuoxhN+68d7wniAH9a+G4aAkK8iX0Y06YW+TZ3NE2Hzr92c9+dpt7ZMt4IHPk3/MQen1sLrC1PN3qp5nHPOF+3nZsjLgw6sgE5aTzdCSD4meCkMlPgVLQBsbqNMeWW8FRMhSlvyfW6UNhU5QGgkD5mVAznggPJU54EgOnqMKGGQHXMPTawVASDMowhMS1QyHLbhjCElCIDEHauhdYhVg5avPQtToPCb155/673p0SwLZXlc1unBkTExVp0X6KSH+Z+GLgjC1Xr8+Y0rGSZUQcQcDNajW9bM2D1AMhB961H48ccbCbo+aXQVaGe4V3ycrTPdNnyDryxSXd95Hryat/s6NvStFmm/qihQ37HDPETK6BwpAUpPAMUhr3fRKCk4cA5qrxN1f7cJcETi5v81DbkQxyOgUrbHPE/c1T8453y3z2Mzn07nSF8dY/Fh6qMSOtiEfeB0GWXzO1eKKjUnMHwaHD6B1Gw3sPK3FPgTx6L/pkmdDvJqGfp+ZJjkmZJTtjnjz9gACYg5mX/p9cRnPGnDX3GWsLl8ivf8kXrwDZWeWOT+QWabF7TjstoMlJ5pmxZ4+SEKyfyC55CNg536cP2SOLXXlbyMSiUQHzRF95NgJOxi2skRNyxI6KDMjJkseCoND77K05iuxEVvUrWU79q1XvKN0vrJW4GGBCpuN4LeyMsR2WEpF0RPDi+kdUCICBpgjB9wwy4TRghFXnWzVRHlZ5Bo2Cs3J2nXtS6FagBo3iInwGkbIycBRs77qk6LQt7kbtoUC1n6C533AF6W/uNSQASQjeKyheLN+/8xJWh0jBsx4EleAzdPpxvxEDmJwWbkkTKEpNvyRXyBjKHTKRh+0kL8bz5JNPbgorW4eXBWWG+CKWElbj6jWOFCIyu4hXYC/wrhQyg0q2UmStL6xG+ZgbZI5yolSGMDcoTXOArFrx8xrlMMoQhf7dY0gXDQEtC9487TC35NNom5Ucw9wvQsw57uzMLX2OkJJB/WBVTamSGflY3hURs8KcVa3aqpKhy/xwD7KkTzwzZCy/c19GxWqdp6+H58w6TTzzXJ/SM/71XPJtPIzZIsRFG4QZ6JTdVMDeBMjZWNI4uYrhI38Jgw09d8IZCKY+ppPdy7ib1+YGQ0s30UtIgARWpDC5Sgx88jH6Z0euV1HEjaySb94/i1o2hu7SRnIe0CkIhPaC/hAu8y95MLd5NKQTkE+E1cKRJ3GZg2BzOC7ijPDTIzxd2kX2ySJ7SEbZUHKuv330D/k3Bt5L2xCm5OsclO3YayUuBoZgn3HGGW2ixu2WLW+MCmVHgHWmzkU0MNRUO2Rg/M1gmxiYKybsHu7JOFkxGVgTyHcQE644BhIB4cr2PIOcYki8OGBCUCSEioeAUos73u8STlj3ABNOinGRJMd58D6UhrAWw7LfBts4pCosYoq0DIumGUPjYnwZ6sRVexhT48M1b6Vlwu52NeVeZM/7WpX7vz419sY0RQ9XGctFkCg3cm8sKTjjELc6o0qxqTOBpJ977rmjxIUSROAlm1Lu+htpYLj1JaWF5O1me7g5amysKJEIfeX/U8cnJL4ehcwrqB/NY3PUfIwxSWzfNQnbmuv63t+igK+77rr2PlnVpm4HmZpa7fubtiY/DTmktI2nezOGQjti/N4nobWxnWuIDs9gcmSG8D3zMEnSyYczrxLe8EzjqT3x8g3vlTDbQcLUQZPeDzG3KDCXeZvJYYyrvqGvbYn2e+ERdgBxS5Xo5DYaJ/lu5JwOJxe8ZWQ9583Nqr2yn4inQkjP4ooeo5PsnrOg6kNi2kaf5ViZEDnkxRzgBVFjxmLOfCLbdJs+JS/efRHyoq/YqF5v6/98l5z5v2vSf2Tc4tzv+rxPcozwIDu+36cS9EhFYvchz5s+bHjtoSIdKT6q03hZUkWQAFDsBjJJrwYdCUE4rND9PdudCb7fGQxKijJJNjpF2HtQTAiGD+EgOMm0NmHcM4lMgRguoUB+UleGcPk/Zewd1j1ovC1ybPYj6cy7Ig3eZRWl8Y0F74nzqBjSsfi9CSIu7dqxMFqSsI0FJbZf5d7JDY+ZRFwGxyQ0idex5Q9JIc+MM8PsPCxKLgXg/D7htCS4jiHlz0P+nvOc5xwLcaaoHwOyG+JCHiwg4p2krD0DaR/bcZXcBitpq2Xz2HiZI/K7LD7sZkgNIZ4T7QtZMK7mVvSBAnti/+TDOwgjubfx8TNlPwbGRJI5nUHehHiFISn55LF4Lx+/Q3R4VZ2Q3lcy1Y92ZiC05vvYJgD6xjOQIO9sTiKYPJj6SR8iZjnOAcFMKOMwIwe0Ih5I+ete97o2xx75yEe2/rnyyivbLi66zLxHvqdCp+SCkT3rrLOa3ChOJ8QonEw30wvrANm2MOYlRJg82/sZc4n+xtwiAdgYC+TMW+8Q3ZJdbGTO77P7zBzTH7yr9NIiJR2GIKNClkJDFuZIHWJlkWae0SnmoWeksCo7S46Nh00nOQbHXBkDcqPt7sNu9Okcm8BaiUti4Sa2+LLJnNhu9pv3pCBKzYor1Tjzt2RqEwpsMase9yZY6dRc7769Fyb3YMSHResoaO2z4krogmL1/CRirZO4MEZWKQzbfnlcco7MfrtWjSdDwzhx8xL4MTe4CTX1N+NO0VmRMXpTK9/dIAmgkYPUElrHeGYVxBtBwVAc+kA/AWVIeVCOZ5555syE6chgimI94QlPaMaYYqcgESMLhORuzbpHj8whkNhHUSVfTL+l74TuzCcEy04wpCNbVilD3/WzhUR2gJnL7t1v8059If3AyDMSjD6DZsGCxCT8JTFzirjoW/dHOBgYJC67+VICIOFc4PXh+kc8UhdHP1LijJXVsbb7/bBCtXfTJnk47q2dDJFnp2ia+yNh5iySQ44Rq8OKyJHx0X/Z/cKjjsDqF+PLgPPMmAOMKLkyNsaMxyK73dwv55UJFepTuwHNFfJoHmW79LAdff7L2LxOwi/ikSTbwHxy79SFEvbkTTQvfUc7/c680CYLNPIhTzJJ6pGX2DuLX/Ik3GSOZyt9Cjd6T33y1Kc+dVK+Z8EzvAMShQh5DtmTb+ZZPFXmXTxbrkewyHG8n5LMjUNyvYZwLzrFPM3ZcIj7prB2j0sEKRU2511LkKy8xkBIFq27YbAQj3kuxgh7YoKbRDxDBIwx2q+S9n2hvv1CQgYmoqRKQm5yzzqWYEhatIlSSl0Zk8PP+500m/dfNzyTzFsJyevgUqdkKD99R3k5G8uHYh/Lo4oCYsgTOqO8EW1xd4aY0bDad58hcUmBxSjLYY0G9/L7JPVRVL0BYPjNC+/AA0ImkTDKL+FarvU8y9/9LQcmxo09BALke/F+aB8ipn8A2ZmVwJpQoNVgts8iFIhLjkLoEw89hwL2d/1k9W/Bo51WqAwsMmYlm0Jm6TtGmEfBCtQ93JvBEd7LmCT0kXyYVeUWbRv0hT5DQJAMss0T4P0RDQSWl1t4lpwlXBGiEo+GsUpfI8j+xsjqdzKJlCKaQ+JC3s0D15PR3vMOSIm8EqTKMxGSvroue5IDdFMHhf4hI0NdFlnWzhDwMa9atopP7ajSVv0wzyOnX3hG9Jd29jpMP5A/c819+vIInmuuJndUG8wnCxtzI1XY2UbtyEKqn/fa2Mvzpg+EPBqz6YAiRdN4WyjRRREvgn+TjBgQxFQnzf/3o505jIynxaq/rzWT5DnvMkZkTArKQZsoKUabK5jSOWwnAue8q0suuaQZSPlbQhMUvVh4v+13ODYUqu/GHZ9dCFEwVn0piz6VIOp3jIvnWXXFzR0YA6TRKq0PnwbGA3Gyukw+TFZew8qfqVprZT3vlGnudQpxqtgVuZi3Zd87C1MxFIwl4qJ9VqKMqf7t39M9ha7IGsWuvfK+KHXEJytzxiDF7Iwfw0eWEU/vxiuTrakB74o+YhSQmlmer8MEfcbI609jIPQg7Mjo6SdhUTLclx2ITDHKSLHv96t5+koYRb+TD3phaLgD3zVPPAeBGRKXHD8QQjxEPII5isZzLaAQnKHu8nzPIUOz4N29s3cbKzNARsn2PBkhx9pHJsl6n9MC+i/H6Fjs8vZ5tjlOxvUdPRu74vfGwWLTPYwBDxTiYkyyCxNCNOl1emPTx6sUcdliEFCriyQdLgpGAnsmeFbf/XcJpNV5CnHtF3KCNkU9TPBiAE00ymKMvFgRmAza5GfKxuewr1IpGivAJz7xia1PKLBZOUeMstg0UBzD/pEsSNEq4pYDNYdgUJTjt2pLkcYelJ4iYZ41ln8Q93eS+7RXXRjXjoX9tHGR4loUO5KjBs0YsotnFrwz7ywFq/1Wk4wQ5a2d/XZTuUbZVutvIcgMpi3SKRvvuQwwufbe2uDejFXCyH43HDchZePhvY7iMQB0EFlFgvVT389jsqC/zjvvvCZHY3lF5FQ4NOPiXmP6ITKABIx5MZCHHAA6huyuCdyHLuqPJAimvIdjfWExglCPLdw8U7/M03eINn0BY++mLdpLh8orSvXczNO+knbK/dPH9C6yl2RyoLORKfltOUswx1+sIsVgWRxuy3DAkYqzy1bWJKSEjtJw2FnqfBB0q0KTyEpxv7wt3JJyE+wY4ModGrCsMrgmESm5HTncjKEV/5czES8CQ3DYPC1jSILtojsk5oVGKXyfWffLWURToNwo2nkekiDx9b0ibd/LGWB9SQKfJF+P5TqYI2MkMUnhPXK0Qkibe85754QN9uOoj4OIeKcWTf7XV7PGfmxcpq6LLI0h3t9Fa6aMlbhYFumLvWLWe0GI1Lz25iw44Xz6WP5NiDgyAwgSb0yeZ3wW2eK/LhRx2VJkSzEBE49fpugcZh+2HaSWh1UQj8t+bYFGQoQ6bIUV+hgjWFa+vDBWAxi8Z9shwAAgLfIL5pW5LxSWwX7mRfEWCi/wRsXdXigcZFiYIFOShSWZpzAoz7nwFw/4Kup77ReKuKwAKVGdeg+7KS7F2GPDtkCPFWabhWS+J8wEhJQbnEDuR7w9ZebtqrATQ17FFPSDZEe7jWTrU/4SxbhgeVqm3LaFwjZAuIenkszLoZi3qaBQ2GbwngiT+pcssxVBjoCxwN3GwxWDIi4rAEONwUqOkiA4daDdLIhBqvOBECx7qGKIgu+F8BDCCy64oMV/F3WTzgJCJmnRdkfJXfPAE6NPbC20vf3FL35xY/1yJTYdLy0UZkEI0y6wk046qbnOy+NSOOgQ6rQJQsL68BiY5JNtcxXdIi4rAIOu8JoQCuIiTLJsaCaZ8bwU8kGWIT/xhqTIl1ilDHufWaXMF4W2qC1z/fXXt91Oi5yzkjivkJDcGwmU2UZYKGwz5Fstcjp1oXAQkO36PgeVhBdxWQGS4IjViiHuJtEU4/X97LvfDXzPatEOCtvZ/LzXpFekhWvRlmf1WvqTnqeQE78RFjktXJFHIfm2UCgUCvuPIi4rgLihuhG8C3bbSEQd1riYhdSO4NUQ7hnb+78IkB5eFlvj7CTayw6HeHHs81ebwXkyim/NKjAHCIpdLraGqpGhFsGqDzMsFAqFwuFFEZctRKoZOiFXXsiyp0EDwmDbq5oTdvLsNV4pDirk9cY3vrF5W+x0mkdaQJiKx8f5URIbF91mWygUCoXCGIq4bCGU91dRlcdlmd1EPRTekgSrvDYCs5e8FuEhXqOc9GwLdLY9C2fxLNmx5CRtlVt5iHJYnzaoVqleC9Jy2A+aWwRq8+RE7OEBlHJ/1FRQhydJ1DxwxkAhNOe+9CXKe+TwTDsCps5pyZlAqmNK1OaR6+u62MnmJFyk1OGAKXg3D2RVvpMwIpkld6rHLrOlMiegq/qpHdogqZz38qCdonyUoYgZuVYThN7IzkYQJuZ1pQ+CJO47D0fNqWE+H11iS7rdkGS2rxo7hA0R5NDcUs1YwcVedtQssRPSYtABjn0F3ymYM5/97GfbYjKnpdser6wEvTevDpP3k6do3qkiLO8RvId54miCwnIo4rJFMJkYNRNLUu5uT4KWH2PCqo/CEO61CBYjgkip1cKw9KErRo/xU32RV8euIdeo3uhQPDktihlVTsvvgRJ0EJrTZpEXIUGKMEfPGy/K1+mulLuEUMSF4lOZ2KGDs4iLbY7Gn4EYFqtjHJACJ6Qjx7xgEsB74mLsbrjhhkYaKOR5xEW7lcc37sKi3g1x8S+Cy9uGhC0y/q7nzXOfHF6H/Oof3rr+rKHCdgJpUSFbbRDj6GcyHiCzxplcqQRLZ5AXHlxlFRDgIXGRQGrsQ2Lpm+EBf+aOnZSIiRPNkQTb2G3v7YkL4v+2t72tPVMZ/HnEBQFzFpc5gQxlvtJvjsWQO0g2Z8EOTGH1yHYOMkRchN5zHtNRLVa4G6yduFDCBpLCIzxZuRu8fBaBe5gkqSpLyeVgs5Q37r0MrnF9r/RNGkLdX+s+Kf4WYwIYvuvde1WHTHkngmzSMV67BS8Ihb8fSbD6wHZnhpbCGYaHUs3RRD7//PNbfzE6yArFwPOzbaQldXZyovi6jhZI3yCAPmSSQpYTRQkiFlaLqg+rIpozpZLz5PcUO09KjpWPHLoXgokYIb/K+oe4GDOyT2lLqKa4yZq5MCwYaE5S1qnaPA/ajAgxOlaSOR2ZZ867IkLPf/7z58oAMuzdnTTNADEO2u2e+s33eYAWVe7ul1Lz2rTfnj79pg+1UZvKk/h7IMcqsjptmPcE6dA/5MlCzInIZNjfLr744pa0n/IRPBrkxXjxzka2kXbERoFL988ZWGB8jYV7IwU33XRTI03mBtswDLPT6/EKG7954CExV4XtU5XWXKIL/Wv+ziMunoXc85jS7TlvyL0zB/XFIrLdFxeN3ctxAfrF38l9jheI3fLvmAfWPUIUPd99fF/7cuTFNmLtxMVgGzBuQSvO7EpRGK0/YG4eCA7PBE+An3U29x02zmAS7H6rlyRXbPxVr3rVMZIjYfTpT396M659SWbKn7A69j5uTsbF9Y5YRwpWsTXSO6jfstu8lgCJsCLJSbV7wcc+9rGmbEy8sZwW7X31q1/dxlJfOk8kB3RRStso+CYqxYkM6CtejnWAkuKJ0KcIoUPneD0UN6PchGgUHNQu82RKBij1Zz3rWc3NrI9dh+j6PqXNW9eTDn/nYbF93bzbbfhxDJ7j3vKftMcc1iZHTSAuPDyLHFdBjpz+y6gYD3Kkvy699NLmaTKfkbV5B9oFDISwFWWun/f7pHeEKt4BoVKr58JOCxcnZKxPzj333Lab0FgipbwXSAh9MSaHOePozDPPbJ5ABpenQ5haeBN5IQvO0wpZ9Cyk4Kqrrmq2hbztl97hHfF897TJQZiLTXA+F/lme+bBXCbf+kAolxca0TIXc6jhomfRuYfvsF/mPL3Bu847i/DRHXQM+fQ3ci+k5d+xPtF3vKXsBG8YD5Tvs4E8XPMONt0U1kpccmigVZ8aJ8iEzmREDAg2rAMppynPS04iFnNU/Ewc1QShQAit1RovCpeiwfRM5AhjtjI0KEChIQj+VZgtsXj3ZzzsnKFIExaxmjXhtPGcc85pz9jPGiTYv/5I7ZfdAmFAsBiR3XqF9IFxolwoDMpiqo6M/jF+FIe+ftzjHtcUuZ1DU3kWm4R3M1m5k40vV688nP04S2QeyCdDbpx5pITSKGmEW9899rGPbUab0c3vx0BpcYFTWAi1+ZCzXpAUMppqzcbH+954441tjPp8g/2AfqPw5B7w8PGK8JaYb5Q1grZIErd3FW7MOVUKYzEYOcnW7+YVTvQshoZ+MbbmPflDfJAXuVYhGGRafzhni2FFHvUhckf2lQ4gx96HcXIP8yFeWit/hsO8FZJQzEtYbL/1wkFBil7qV+EhBMSBmfQwA+jv+s5CU/8KUY7NOQtC1xsTshAdgoQmVNN7zY05T+LrXve69txldm8uAmPrdOgc3Il4GHeyiLQv4rUhE85p817J12G/cvihOTzLY2dO6zN9Z5FArul2c9l3tYu8mucWLuY6YkQv5LRr8imMnBCbe1jIW0TpN/fTLm11H/o+B/HSM9sm02slLgaA4DHOiADlTZlQ6BSNkIQBIBxTJ6omlkmJMAL+b3Jg7+5h4ri/RC4DRiAIGiWF5FgNUrQGh9KyOiBUDK1BMxEwYO3D+F0bV5/fGVDMW9v3czATooqbbjcgfBQGQfPZTRuAYdWX4romAiUNmVza1xsjE0R/8szwnDFg21oNNysS404RglWGBDltXuUElahISRhjxCMnGeeZZI18WuUgnlMHKpJHMkqBk1njYU4w2ty9FFAfmslYeZ531Q6KcD8gDwYBM1+9EwKij9OXi8qBFSFjZQFhjlG85hxjZ64lKXMK5q33suhIDoO+cB9EUJ8hdrkHxU3fCGtYOes/1zsolDFCHC0AgDeJd9d8cI255V+Gw2KGUTUH9C3dtWjoMSUGFiF22wRjOjS03p/esIjRL4w03a5PyDHvd4gdckE3jy1OjZsFpXmSU4jp3XihU227v568GQdE03UJ4+wHjDXjj8CYk4iV+ydcO+vQ08B78nrw1gh7eTekXj+xU+bPrIWT9/Z+PCMW1GTd88myeaNNWcwj7Tyu2uq5xoS+o5/pBNd7FrJncYG4GBs625wg5+SdTLpWBIMD4EgTF8LECBJEHWE1c9FFFzXF8UM/9EONWOhkyia5J0NQKq5JfJBAnXHGGe1aeRg63gDq8Gy/JSQmlIH0O+XmXcedTekwAiaYEBDBMln8X8LUc5/73DYZxGxtBaZMTbz9Vjapd0KAxPp343XRpwwfgfbvMsj7eDfuXKxdvBhS9RaRM4mMj37q+4CBIegm8jbG+9NWsmayIrJgJZ1kVhN4Kha8H6B8QgL16ZAo+b8V0TDxcAhjxO0+BGMaEhaFmvyjs88+u8kYuRLaQ/r3A5RmEnizOwQhoCgZHnLY549BT8yzonYNQ5ATgi+//PJGQoyNlaK5OEumPRfJ5sIHK0yEx3hbyNAtjASdE4+Vv5MFMkBH6DP9E8+RT5DcPP9aXLlGu62CESb5GeYN0rkocTGXGAmGaJnT3zeJGOxZJ4znul6+/WtuzQv1mR/GhG5PqMjCk77WR4ghPR2Z8i/5lh7Ac0r2eNbZh/0AO+R5PkiS8CCjz5bxGpGFIHLd68W+H/yLSJBTBMTPZPvhD39406++N7VYN59cz8uTk7LJp5CZhbd+I4vIjcXDM57xjGZPeGiuvvrqlv9jUaD//KsN7Kj5hVA+5znPaQSfjdPXeY9tJdVrJS4GXeca9DG2TfkQCsoG4RhTVJSH+/SZ6j0IjwH2oeApT54AyiVCSEFxsVFeFA6lZcVlhSXZSqJUVmwGn9AkHut3q/AmJORiBZis82XBMFGcu919YYJQ8sJDJkBAgXDdC6npU0zdNcgL6BMr4gsvvLCtmucptU2B4mOwGaqAzJmwJjaye1CK4xnreOmiMLWf8pZn0h8ESPlTWJTibosZLgIrNvJzxRVXtDi8fDV5T1lNaq/5S/lqc85FQRiHCttqNImLdlJZoZPrqQNC6QNz2DzVD1axjCRiYHGiPcgLg2YFaZ7INfA7MmGO80JpD9LD+5WcgCRyZnEhHGo+uDfZV4zRz5Knl8lN02bnkVk4DbfFbyuMh/c/77zzVvYM40hnhwDqe89FFJ74xCe20EjkhezwtFjA0u9JBVgF2B16j+eNVxABYEMCcsK2hYRqP/vT2zo2DelFFpAHY28hLWfNgnMR0st+6X8y7r09j77WPnMqyc0WMfSbZ5qb7Arbag7Fi+X7L3jBCxr5s/DU/hCXbcZaiYuBpYymWJxJb/Wh86bCJYl5z1IQBtInIQ3PdE8rhewwoISi/IWMku/ik9yChG76uC2lyCjsN3lJ7s6icdMhCDylKlSTjPtlnu39hYdMTKuWkBJ9ZaIJx3ln5Mr7U/oIgDZzgdp6baXP8K9rl84yIC+UBJKij3uC4l15lxi0VRIXhjAyR66Ms3bFQ0WuKRREmjJGAMfyOvzOeFA0VlrkkxG0CqNIKaGeCPg55GFVY2MOId2S2skIpSlvpN/ZxpvBG4rcUPw5sfwxj3lMIyV98qAkePONcvd+PJ1c9FPEJXNev7qWt4YRSx/rG/2WvqYHkCHeIoQj9Tl4YayCzaHMcUpf/+aMF4bAHPBeCCGDifQsSwoZXatmz9zv3IxVAcGy+BtDduiN6Ua6NIY9Mj92bpoxN8aeoc8tLMkTWeF1E7pJ/lyeqR+zEWMVi0pjg/jKf7LwZk/INU8HAhw7YTMHEozEgrlofM3VgKykVIHFtflAxpFsurv34EyB3LkH4qS/tE+bQrDphCuvvLLZO3pd2/1Nf/pb9I/5Eo+sf93roCzcts/CrBkG0YAOFUcSoniAKGRufpPp5JNPvoNhANdScH0IhYHk6fHvvPBDVqI+u3EbEzrsWSx12R0OlAllb2IiIzmNmlKgVMWrtc/ExNgZGJPCqhTJM+EkcjE+25rbAvoVORnbdpjV/yrBmMtpYSjJE4JCSfudtvk9NznvjzGxqh/b8aT9FKIVKMVkLFI/xz0ptSERWBWyrVq7eeLkDfG6RRH3XlPXkTOhUDLmPcw9yY/mD/Jg/kSWEQmKFqFG6PRPH74ZQxLLPYtyNq4WG5S9+YsM+rnfEp/5Gne+segXRtqV8LDrQ5LMD23dLRlkjLXtIMF4jMmVPmD0GF4LKH2PaDKujDV55vmiD425a5HT4SF/rpWf4SRuBABRENYlL/24Llo2Y68QFufJENqRF6cNyKrQlLFjCxJS8TckITtlyRDZ8e5klwx5P4TGIo/u9DfETL+Yt4sQFzJqXo31QRb2+h7JND/1NaJNl9ML5DxbpDkKtI0eyhb/MVho+FtfXmCTeS9HgrjMSrr0++xfhwghgUVaxMwpY0aHl4EbfmziEpRkaEfpmWCEmADNC9+YkARorHLkIu9nAiEPw23gsxBFTBlJdk5OS+6pXxgfQip/SLw0St4EO+2009pq2SpoG7c99zC+w7yFdYMXBfGLB48ipATsbKLUkA9hEV4hq9GQmiGMh/FGXKzchOl4PBACSotC5Ebe6+qJUh2GZJOroN36lOLTXgmxVo/aqyIpUsuAkWsG2ncobatm8omImB/eEZmguJFm74AoCwdQpN6HzJkXs/K++lwZc80CQ/zfd92bfCL0IfUWCEgUspUQURL8FQrTdz7xwvok1MWI6hc/Z76mhlSg3X7vO953P0oTbAOm9Fjyq+QQknF9a9dKVvPZTWonaPKIhEuGuoqsIDvCdcDg6ls5d8gD+eHl4C2DvfQpHT+Ub+NsrMi3sUtRRGU0XO/Z9KwCkdqetAcfcw6pyT2RWvoYeTGvySF5Z0O0P+kHPZHYLWLDtJ3c0svmFfKXejp0OS8ouCZeH/2qLIPvJwdvCAst12qrd6CfNqnzDz1x0dFxE0/93STKRADCSIlSxoy1v1OCkqgM1thkISSuoxgT5qLUGShGZR5MECvtZUkLJG6KWC1bX4ZgU95qgPSIByIl5iXI9SE+ZEzSl8mZ2jaF2UD2ECeKW0iOoafQrSj9m9UoAyD0NhUW6UFhup6hR37EsZFMCmovxAVpYHiGVXopSMSIl0SYR7vJDxlnyLVfuEiOQq495ZRTmsEzN7y/UAylTZ7IGBlC8MlaKvCSS4oVyUMCeHFmeSfM7yRX6wOeJ/1Lbs1jXil99KQnPaldz6Wv3XJeyLr8NvPIs8X4kSfeOYYX4dLP+oQRuuaaa5oiF6qTJO0Z2TWSBRACJFxlTOSEIHLbmLS+3zBG5FiYjkE0rnQrnSokQm+QG8Rk3vZ2QPYZTGFeZIg88Byceuqpu25jwvI2XBijHiHXiK82ex6yhbSkgCR5ImNkQqiR0QeknYxn4RodyovoXdkCO36E4s1tJF1byDkv025rDSErCKO2ap92m18Ii2d4pnlI/7iOHApz8Q6xc695zWva4oPd4l0ag4Rnc9Mcl0dHPy2bkrCfWCtxwZ6TdW9wGWmDmvgwxWPwKTkDrfOtjChDSpBQEQQrTd6NnOUTN26KbiUhynN8KI1sAfXxHaQiIRyuu96lLQZPqSEtBNZEocC01Xf8PEwo9H0C35/NQukTXspwVvhHPyAuhGw3xcGsuBkDk2FRFpytmNpGeCmFHhkfE8HY6K8eBDiZ7sO/FcZhbBhEKy59yrgy0PqfDOd8JyEiK7fssMmKjEwPxzdb4BllBlRiI6Mh6dR8WTZROwmoQlCpWkt2tc+/5J5Bp7BDlOymMUfjqaSYKUcfpMr8y660Kfkku+YZ0mDVp/Kua7WDgmQQzfspUMzIGhe+/vR9oQnt0s+25iJy2kiuGRGeVP1npWwVrb2UPWOLeNBV5rp36PvRnKAH6Bb3ptcQF4uHkBP9og2ez0gjRkeBuBhHfZn8jewAJcPkxRjK+chOGtAv9DvZGobdYtQVpOP10N/61TwRTtxt/SVGmn4fkidjSUaEqtgKhJyBDxlJ1VzEnHz2oZ1UER/CdfqFjeBpNF+iV3mrhY38O7W1OjlqfY5WD31Gr9Ab5o4FgOJ2dLT54zlItWeksjUCg6yQ09TgseidOhMs3sykCWy6GvpaiQtGGe+GjmIs5Y8YTB2e8smUkEFCFLJyIhCUOQWGIFCeJgXFgMkbJBMkFXEJSrbmYu0YO0Us2YtypNRSWpxipNSSZ0IoKd/EKlOMLRnr3HAISk9cCNZwElmdMSbaPou4uI4AmSDLJuZqg/YjL4vUFAi8p9AUNyhBH5KPxEqnEg6T3OjZq6gifFhBzsg4uSOv5Jv8G3fKh5GnZKzcYuSz/TFVO8l0kkOBzDOyXO/GFRnKERdDIDnmYM6zGsqs9jHk5oo2ei4ZyOLC98xPMp1y41bQ7juUXbLJ8C8SJjFfubKR4YSR4pZmuJCSWSQM2dI/2qht5nYO+9TfyQkCRstciUeFkXJ//WW+0hGelfdJSDU7NlJITF8jLPSN+yM4yfHSH+aH/hvbNXVYwajp72xyMJbILBml/40lEkkGA/JBnu1C08+99xssZhFS84WO1J/mwdgGDuOZg2XNoSGRMEYM/JRnG7mIpzLySzbGFmfecd4Bi2AeIVkInf5JOMZzctBpP9+HMN/9Xb9GpvvE5uS8uI8+0SbzlQ7wsw+vUA5uJc+enbBW8lay+4h9TMgsbaKXsqPWz+R7k1grcaEsGHwKituJCyu7PAyIjlfhMjtTdD73lwxpA8J9h51GOFM74RWveMUxLwrByHUGzPcoLMqGdwEh4eblDTGhMGZEiGBQXBi2+6aqL6iy2oMgL+LGn4eEXihZLH43hyomprlM3RZ9gigJDyFpnr8MUgdDCICR24++OCogU4yiD0VmRWQsGEkkcOwk7xAVhNnqnay7dqg8uH/NC/OGkRgLFSUHxerXs4bXICGXXHJJk39KzjM8j6Hwb/JbGBfzmdFW62jsiAIKkZFBkOat0FwnHMTrQnnmPBbK0u8WCSvoU54nxoBO6V32ceODdlv1Ix3mAmPGGHi/pz71qW0+eM/0DR1FL5B7K1L9R6ckoT8e2z5ZMgsw40rnbXPS+n6DTjUWdLC+jHcqu7GGeS36TR+p5cUODBdCZMD4Pe1pT2s6niyQ3THvhn43N1xnXIceBHOOAZ/alUpO2RCy5z2ERdilMaKTInDzoL1kkt0SYjHngX3yHvN0tzbpH/XKyDe7kSNdengv7+4dLfrNIf1O3vuCf76fCvNssXa5vz7hzQLzQfvSF3SLz7ZgrcQlBdIYPJ0n3INB5/RXORoUbwRSRxNYYRCdaKdCEm1NCoqDsuH2DVPHpn2ypTk5LlajJgWvCW8LpYT5U15ITU7oJQzYcbatjkFb9msFRbEhcDw6y4JQElQMmHJfFIRaP4hbZhItA0pbjoMS9RTRUVlNrgIUQ4pPTeVPBWSWLOfaoduYgiLHZJ9sjLmVzSlKL4eoDV3zWf2ap0nE9TyGKAWyshoDz6P0xopV5dpFd92Y955tfuVey+720l5zYrhbaKjkPSPEL/dPmEw/5t3HwNh456z4x8ZC/7lPDmE8anMkydhkm0FMf04RWL9HFHIw4Njf0+fZlj4mV/rduGaODAkjQt/L1xDDcY88TJXnWCZkkgMnQ3aWPeA18xKm6onFZma3Ux/iCYyH3B7hJB5GfSJniCfIQhZ4I7PlehuxduISt5nVo9VakpwYXoyxr7RJaBALCts1BDsKwCrH6pNCletikAgE7wkPQFZoEfIk32XLqJ8RFkrewGUXjf/z2AyTEntQjPuhiJIklrj6sjBpvJeVxSLbA7P1m3A6zZegLnK8QHYMWKWafMYKwTQ5Nr0t7qBjSgGPIbWHppC8klmYd0120AyfM0UeEj7ZD0w9exlEx8zDWL9PGUQ6hfwLWee78955mXE9jJhFLqaun3U68l7GtUdOeF4U+zmOmXuLnnA+xCJtjx2bdw1Skq3bPIpKYfCMCdWSdTlsFqiL9PkmsPaZlcPghFvE2BL/xM6HncRIYnxjrC8GFEnhxmaUKZOpfAukJqtGLmnPGuaEJOzCm7MupC7Ebk6D9g68UYuebpxTgmXJS0BehLTkrBikxe4Iqxl9nGPni7QUDjtyppoQHNk/KEW6CoUxJDk3OToIOVvALpN1C3MpG9vqbYGNLQlSvGkvST5hl4vunEith20pSZ+6EH0S1KJA9gjaVJGyIZAWISKHyMn1meVRChLDtQtGVn+ffFgoHBXQUQ5WVW8niZCFwkFFknEt0BGYPl2AXbagT5G5bcXR9WVuARAJ1WjV8RAuWgbJtE+BpnmQXCg8lEMs5wGZsrp88pOf3HKPxqoFFwpHBTy8ObF+mxV6obAMcmJ0kJyYbV+gFnHZEOSa2IasmqQaM8vWb8n5GBG0MSQBzS4ppbMl48omX+RIgVQalcsiHLfbuGyhcNARslKEpXDYsI6jTlaBIi4bgkQoNQ4UChM7XxaEjUdkSpmmwJyscaSFZ0fBrUUg3whZ4UoUHlr0CIFCoVAoFFaNIi4rQDwdiyS/LnLNELwftqupCTCVjOy+yJHy6zwti5IWq0tJWcr42yInRFTYX/TykYP+gn5XzTA0lxPP890evofE9t63fD/PC5n1ySm+yfsK0qb+nsu8U7/NdHjvwtFAtsZHlrLDKLIwlIkx2Rli2e8Or++vG56cvsi7LNqewnpQxGUFMFnVjLHbaeq05/4AuWWhno2EWWWvp0I4QlHKljsvRHnpRSHxkKcFcbH9/CC6Ebcd2QYv78jW/H58lAqwFXGs9kdKdDMCqh6nqnFK69sR4N+xCsqMiCQ8YUlFG+3qs3vAroK+eq68KyFMbfT3RYsLSjLXnv7guJRxLxwtkAFyJG/PgskmAtXLJTnnKJYeqfJMhsb0Yeq/+O4YccmxL0FqB+Vwz4Au9gx/W3RTCJkeFldMUbdtzwM5zCjisgIwEArK2b2jIq68kuFOBJNIBd9lt0EjEoiL7ZlTJf5NYnkt1113Xatxs8jBjSYj741TTyX98rocxcJZq4bdXOonqAiNIBgfVWoD/U7h86aRGeOCdEioVqjQOTwUqbL+KUmfbY0StXMWjEqdSEMUO7IiCZxcIj8qSCOm6jnYMUPJe5ZS/w4O9Ey/n0dcKHa1H2yzV9jRz0Bu1BjSFoUhj3JNk6MEeseCiWyrEUKWEQ5Hu/Dekgf1ukIcyLJwuaNHLLbG9KHvy7dT+oFcSyaNJ8T8cZwL+QuQHHPHwbiKLZJtc0WtEtf7nU0HvRdoDDkA1acv+W9Xqhpi5tp+FiMtLI7SJiuAFQQDxSDxugzPcDHhkBsVfxc9mygHbZks6tAonjdEJjPDZG++YxUW2fZsoiu8p7S1c1sYnE2fRXEYQSkjLSpW3n777Y3Q5hwiQGSNHYXPc6L4IiWJRJAjHhcnNiO9VrH+hpzkvsiJjzF/ylOe0v4WWXRsBe+b69Qhce6LcafI1VNiEIw5QiQnyjP782SmoC3I0E033dROXM45ST48d+6ZSr6FwwvjTRYQa7LN05KSDcgJckHOkQGknA4jf/7mWic1Iy59qXkLrhB0JS/MC8VBU0cHmUBYnNZskWjXV4iPa+y8tLgzl/yeXCMhvI1PeMIT5oZBeULNG7KNoCNDFgEWdHS7k8bJ914PHIzejrdyXtE3c1O/6d9FzgE7jChtsgKo6is/xLkSJtRLXvKS41yZJhGjZVWyKHFJ9VrndZh4UyEcE4wB8VyKYAqJO/cHdF166aVtVbRflVALx4Nisrp0RpSk6Rw458gGkI/kgDOkAslATEJcyI/x5HkhC8ilYyycA8RoOLCUknV/RoDnjEfFM1VIprSFpoR/HAioejLvipCTozesaHdDVrVJ+XDkhSzz0DBgnikshaQ542SqRHmQ/Bvv0pfqT1l0Pw8VfF8yPfk/CRO4PsUdUyYekhuU/J0Yr6Oo/PcLOXFbqQWeFUQEaRYeQlAQcvJM/q666qoWRlKNGDkhM/5vIZdzqegic4O3BhEi0zYyKJyJTOekbeRBIU1zJufxmCfu5ePwXQs8enM34BXlQdJGZMpcpbf93hzjAUq4dQzJ8UmeTx8Gy/EekXt625zJ4ZSRzX7O5F6u5cnXfz65Jt85CrvfirhsAFbVJrFJtmhyronOvWlST1XupKQZC5PdCmcWrGAcsMXwMTb+rZyW1YIitoqzchQSctaTA9Gi+KwQ5bggGakZAv41LlajlDtiadWKgORMkihV4Zoe2e5IwRpjZIebm7vcVnxt4oUZO0l6EVCkyJRneBfVlRGXyy+/fOeLX/xiI2FkUXhzVuFHhg+R5yXUFvOCnMvjcmowUkVhM4KSzZEXc0LowfszUkgY46Vf9Kn+MBeQulTmRhhB/zOC7rHtxba2HWTAuFxzzTVN/siZMA15sChCbvUzY4+k+B3d128syMGtDhJUtRXxMcbGiZyqQWXe8B6GoJIZ90IgkCT1ppBxBN53cpjubpGTlulcOX9ImJAWgua+yLpNEp4/BkTENT70rfZ6b+9mnpBv95HnZs6T/5y+7H2cdt5vjqDbLUqF4swtBIfOjuzyxisoR4ccdhRx2QAoUYaEgAkBJMlyFij9HNc+Ri5MCCzcBBcmoiDGwPgJDVDujJiVtsk/duTCYQLlKtRi5Ta2/ZzCcNK1/ljV6pvi8bGCk49iNYhAxGug/yk1ckEpUeRAMRl3RpkCZAgoZfkkVprezerTmLu23yafAlMqH+cUXgQpxIhyplB3s7sNyA6lTslSnGRU+7RBu7wrsjVFDPJ8BIN3Rh5PDi30L0XtHZEMfeN6IVYE0Fj6HWNl5W0uMZbxyJgPvFsMnvcl+0mKZ0yspnmmzIep3XmrgH5hsGZ5RLcZVvl9zp6Qjb6WN8VY84gwvoy6MYx+MVbGmhzr76EHLl7g5HSBPjKuOSgzcuS75PqEE05ouoxXRbiTrJAZMM6LerTHoCo5Pe1ZiBcSgYSnDfOOavEOdA5PEeKd5GNzXv6YecF7g/AhL+TWO+pDsqn9IeHIvP59z3ve03SIuU6u/Rxvvmv0bRGXwkpgIjOQY5N3DCYjQ8do9bkCJjilYdVstWkl8O53v7t5c4bwHMpb3gRDo3w5t+xROW9IX+knK3qu595Q51Riq5xFjqnfLaz2edv0eSqx9uNpnCl9nx7Gx99y8i2FxdBTjBQV5cl4U2KuYeSzU8j9KT4J10C58UTwhMgfcD/32G2BQfe2w43y9Ezv5h39nxJm5BClqfAj5e99rDitZr2TVaO54T7eE7FA5Kzk9YN5gJzLV9A3ZN8H0bOKTZ96P9d4hvfTDp4fxNX76zPjHkO6LjBIDJUQx0GD8c3mgCDJ4uaXn8m1/oxe0ffG5sQTT5y8r/mIzDHO/cICUUg+FmJivBIOQVx44/J9xpz3UDs827V7ydUjhz4BORWC8izyjNR4xhSMswWFean95IyHBAFC6MxDMiCM5ndSAMg3Ui7U73eutxiwSEG2yb35rl3mnjal1IX79SkJhxlrJy6J86V+RR/P7utGLLK/PjHEYe2IxLj7e+T6fmtynjdVbyL3zXdSCnmvht79TDBCuIi3xQQxaQlqiE5i/VadN9xwQzPIVuFWJ2OrABOF8j/nnHMai1/0fKfDAv3G2+BfikQ4I6Ag7HRYdZiMYp133ELktJez5BD4PsVk3LmLrSxzPfDKcGdLYBw7TydboilFSY3uFxf7bs/fCTFCUNyfXMvVQToYDSthsjblzSP/PChIt7ZZLV5wwQVtVSp35uKLL27hBzLrb54jlJBq0An9MJRW+MJgVvdDMHK8Mc9//vMbyXnNa17T8nx4apA6RmVdBN4YGoOLLrpoLc/bTxjvZz/72ccRl/0AncXTYOdP0NsGMkZO6cHhPI0u5N0gewgwsoQI7Da/pb935hgSnEUPIub+ZG4ecrDwYx7zmCafZM0CKaQM4VcC4ayzzmo6mkw+97nPbUTF4tJCRhK9uWW+8NQ+/elPb33hWnN5tx7Tg4qNEBeGm1LiJsv2ScqGIEhopfDmKRHfI6hcyxg2NxzlSCAkxg5XkQw6RX/jjTceK8BFKFxrlTa24nRP7B8x8DPmS/ntNR7+0Y9+tClNbtBFBM4Kxw6NPoPc++s/bTOZTHqTd8p1SbFz31L+U8lkhxmIACXG02R1KAYO5M6K/vTTT1+ptwXImb5n1KdgHCkoyirGPkodSbWqIqvi7tpuxSXenXwABj45IUMw8pIn5RogCZJmkRykra/lshuQZQSDbJvb5Jonxu6NWfemCxDu5Hv5Vzu9j3elqBH8hz/84e16c0B79Y/n6SvgypdroI/H5qe5bh4lr0CbPItB8OGNWdepz1l977fxXwdSM2hV4GHI7h3y7t8U23zEIx7RFnFDkD1eh1e96lXN2PNaGGtzZK8FNC0YUj7gHe94R8uX4tG0SUL+1SJk1zx2rTbRNQmdmrcIu2cgH3Q6T45/yahFznCho2/YoeQk0gFHwWM+xFqJS7Z12tLJcFAYDIrVb+KaVlri5VMrtGRhp7gapeZaygC58CHoBAArjgvRzgnxQSsdyaieZdVGeYk3Uvq9O5tix4Yl/Ym9U2pWtLspGDeE+y6zFVo4yCfeFpOUCx350Q8m7qzzh/QPJi8HgeAfxQTcbCendCgGCkNcngJg6PWN8M0qlQAZo/Ql4aVAFzlL0qq5QZ7NDXNAzg2iSeYYcArOv5SVxGrKEKGxmqNYETLGfljIy3wRPsyWaETBveUHcDnvxZ1O7swl9zW3hECQZH3KM4JkzNouqq36oZdvc8N7kGuK3riF/Bgf8jwMszEGrpmSbWOrn3ISO8Oh7Z7hs0ito/0CPSNku1eyuAkYo6GXIcXeyCX5NJbkOjKob40xve9v5poF4PC+CWmSfTIlNwQ5ZR/MVWM8HF+hGAs4pAIRcA8EQTjc3N5LH7MNvCLIvmdoBw+lhHD5L+RpEX3h3ZAp1/feQHpI+/WTeWD+I2quN7cRk2FCe+yfPtcXR7XMwFrfOvVL3v72t7d6E+KDFKdYM6+B32HUVj9Wv1MKzyAz2MgIpWNlRyAQIcpT2IR7GtlwD4zZSpBbjdLAWLmLCboibQTctf6mjYyBtrgPtyMl6prEN4dlo5dF2PSiYORSE4aR0W4kDKmaB8JttWmimXRTReuOCqzAhFMYbYrUz1a+68hx4OJlyHkJyZj4NgPMOFPuVnMIgDwl5IKCR1xCurSRAY630JgyFBS6OUTOyS1ly/NCUVJyFK654r7mjXtQiuTYPEB4eAB6Je9v5HToHUqSpHt7rnYjK+7NlY4QcOkjVuayZ89Kzs2W5+ycMo/TjuyG0gfaC0lEpvQZQffWVp5R5MzvGa+h7vD3eHbMPf3GQIQU5frcyzw3NubLfpNZbebm9zkMiKebLke8kRSG3u/0H6+g37/1rW9tuuyUU065A3FJAjq55XUneyGXFmrmTBK1LcKMCVmwCEBw1I7Rr0gPT4t5lq3DQ/IiD8d8IV99jmEq6kZHJukbKfKziACvtWeQ+z5XbTfwnNRh8u7ubWFpPpp35jj5D1nPfDNnvbd3c+0U2Avzga7RZ2ziYanPtVbikhWO1aHBEte78MILm+J74Qtf2LwIQh+MiQEdi7tTLASPO9mEQCjExJEOK1VeCNslKWIDb/K4v8E2+FyOinNR4Ngt42WFx0gYXEAIEBrKPnUlTLisZudVXJwF7x2BXRQInmcKjfEYUNx9tdUeyRVK+8T2JcXZertKF+9BAWXFEJI7BBmZGCbDrgqMr9Ugbw/vx1ve8pamlMW9rSi5uSOnxjnHzRt732XoyDVFFCBiiAKlbmVIloVDhU6QAHOFEvQsyi61UhgRc41sIUDnnXde8wgFDLd5wyD0SFVS3zG3zGceSd5LilJ73EcIB1Fwf54XxmNszpi3DJ55SAnzktoqas4JOSFiYv/eO7kM3tXzzEn3z2Gi7qHfkCbEqod+1m66RfIjcmIekgV6wsIluQyeqd/MF/fb60LlsMPYks2nPvWpbQwR5yy0yAiviXwkv9OPY1uUQ4jJPplgpI07GSJLvkuGGV7hXqQGKbaAQyzIRbw+jDs7QDaMXy/X4F7m31CPu7fr2QK/ZyO8C9ICdH/CRsD2ZE7uBuTefEXK2B7hUPPHItsiAJExH7KDKiE07RIWsxANyR6DeztcF7FDFt1/kaKSBwFrJS5WlLwYmCIDQlAZcINl4CgSA0NApgaDUFLQ4p9JxCXkBJby8aHQ3CPbMQkCZZWzU+Jm83/PofAwdCtfSgpByCqUwAjtEGo/74W0mLDa7nn6YlGYhJR1Qh2MLcOhXT30J8NIcVudU9Z+pqyPWjLuLFB65MBEzkpmHYinBHlm8BEJsoa0mBMUsXZRWAlfQg7MTAG64btQaOeff37zQFBSFCvPjZUrWaW8kJ0ksptjFF68He45zI3yTKtkyq+H9pE/H0aJB4MiZaSAV5KByTwxtz0vNWeG0P9WsMIPiBKFzWB5PgOjX8wb8xjhcn9zyPvIaZGbZAHjvekEixd9PPQsaqd+UQtJX1qE0DlyfLRLP+hfnl9HHvDeMCwKpmlj1XmZDbrJAgCJpqMRS4SCTkqom/cAKRXGmYecdeV+9LmkXZ5mshYPHDnINmJyTQYRJEQAjNvjH//4lhTbE1lEyLjmOQGZ1TZb5C1qyKJE/sDPvEnx4AhrIVm7JS50MztjscJD5d7anNIG7k2OtcszzBMkkIzqCzakL9g4BDKfoxf0G6JTxGUXoCBzPk88A6kzQXmkkuKsPJIUO3Kv7AZyH8SFcaaMKKb+BN4ULornIt+Jm5ASTN0Tf0NgEq81CSm5FABbZPvy1ImlnkHBIhz92RfzoP1cfp7t3bH8YUweUREXlWyMvDAwBJ2B0b+HuUbLsgjhjYdtXTB+XMJczp6PWKYgHVjBpbaLsYzxjauYcZekzQgb0yRrk01/49lIKCXjnXAIWRg7dwjR98zkdyEjVmdWlmN5H+5lnoXs+dd9GfahTGsbA+MztR06xEvowHxJjYpsq2UM9UdquHg/P1PA3kktIgbL9TwlvpOdIJ7JADEI/qX80x/aZLHi+zlvRj96tyT2573K2zIf2TnDG6I/GUqGM4SYPkVeeRfJeWAsjAMyT96TIB3dbh7wzGeLvTGNnJlD5H5skeu7dCJ5JhPGnSclJSTG4DoeDu0nCyELU+d1aessvRqSb87GA9qDPdInZFe0ge3T7hSLlAeVnaT6CdHRLnNCf5Bpsi9MO2YzeQwtWv0NyU+49TBg7Tkuw5UdgefNoLwI7ryiTNmVNBwoAm2QfcZOH53y4OR+/d8JU854wWytXvtS4mOKzKSicCl7q9mUaLei9nv3T+7MWAG0WfDdtI/AxnUZ6D+T0irdisGEGEuiK2weWaFlO6VVE08BWBFRkim0FTmL4nI9ZUm2KLeQgRAxCpKiTtJxlB4iS2mNbb13D4uGKFXXOYNFu8ZqQuT8mSQNeoZE33g5e2iX9vJcTBGXtF2ekXYg9WSccWF4KPyco5RwAG8j6Cvvi2xoAyNh3qaGiO8wfOabvzGAMYwZB3Mki5EU/7N7xbNSSbqIy3zEe8eokk2GEjHPpgHyJWHbv71+Dqk2HnRnii4G7AID7j7+brHR53mZK+bFWHuMNVJEHuhPJJU8TG1k0BbylpC668nHVG0U8jdr15K5YU57BzI6rPniHci2vyEhIVRIs8Uz+STD2m7uprqwf8kpUsJbI1yWPLg+n8e7sKlk3xz0jMOCjack996JvezYyfd3c59eMfk5YZUhAerbOlRmlK0tbYyQBGEudsQl7aHoGQOeolk7gBbB8P0YKWEP4YLC9iNKPt4IK6lFQOn6TIFSGyp+WGbbLUXJkPgsghSg2ysYJJ+QkjEgEYgKgt5Dfwqv5cynwLuYG1b/jAEjNCtMERLFYBV2h+wO8mF856H3yk0BkRjLz7NY81m0Xbw9ywAx8Nkt9AFSNUasAvLGeyo8NQWLfV5ZeS3SHpAlnvUQ9Mit3/fkJKUeFhmHg4a1EpeU8e5hULi7uHOtjOaFYhL7HMaceUeEdIRShiu/bH+cuh/WPm9bmVCNXUuYr9XBkLj4fra8MUQYLqbuveSnzCoNPYZ4eOaFzgAR2ktp60LhMIKylzhMv+Qk3ULhoIHtQth5ToXfEPErr7yyJdjzQiW/yGLjMIWDZmGtxMWKSufa9ZDdQciK0AcDj3zwTPRu8hSlSgzaxz0wT/HwnPvhXy7yFLTLPSgs8XAuNc8z0Dwhnkexucagz3OjDU+uHYJbEvu3Msg1cm0kUkn00zYKdNY9AqSFG9K2bWTMe3qvqe/x4kydTVQoHFVYyaq5IUTL69TnVhQKBwXsgcWybd7sEE9OEpKRFoUk2UT2Yioke9iwVuKCNYpXIjB2ByATdhkxzpikTqdcxAStjng3EBvG3+CJ+YkJcgmL22U3g3oYqUSInCT26H6Ii3irXBP3Ea4RyvFd4R3xUq68qQSswL36w+uGiHu0h7YhLzwxPCJimPM8L4iU/qFoTzrppBZ6uummm44lLPZIsqfrj2I13EJhFuRa2EVEv0jw9SkUDirktbCNdhuyjRb1wqHCwxbe69oduQ1YK3FhaBl/Rtm2NTUiUicCUfH7Jz7xiceSiigcW9Ke85znNINv6+KLX/zi5nUR6zeAtmw6twGQCgbcljvxTLkqvmfAER05KLZLptw7tkqZ+fusw7JACIgbTjsX2Vk0hOxz94jATXlP3F/bbeGTzJa6E7b9DYmLe0o4lJE/dbR6oXBUkTotR+G03MLRAJtWpS02QFx0ugJwCAZPSQqpyQmxlU5+SNxd/kUWeGEY9FQR9LOtn6lsmbwWzNOOoBya1j8T6fFMVXtTMpn3BsnhZhurKMsbI7GJh0coyHW7IS3A84J4zKpR4728LwInYx5ZUYRLQbzU3UgeDS+LjPkzzzyzJR2u83TbQqFQKBQ2hbUSl9SjQBh4CeSEpIoi7wmCkmqhgLgI4SgihGjkdF9g4JGUbKGWO8KNZnXlO/1W0TyTK839EQfeGcZf3JC7bSw51/e44JAeJAaZ2EvF3EXCRMiLnB9F54S+eJSEt3KIJIIntOV9EDX5OUe9jH+hUCgUjg7Wvh06CbP2t/vMAqIhV0WuxxA5pXTRMvaIhxCUz6LQTp4M1RvXgSQaIy2Sr1RJlBeTYlo8Traeak/VaDm4yKFqPHDGO6eE8wiStxwmN/TuuV6ocYoAp4r0MNadUvb5/qxrtYt3UEJ8vHuLwPfcm9xCEumP4oGeRx2pWG4jBDnKmT7kqT+OJMhcmNq44DvkKIXkhvC9eLOziWN4PpH7kmvXZgcozFuIehcy3RdjzPenanoVVo+N13Ep/D6yXz+VVHvw/KjV4tyhdVd8LewvUgJAQrry5A5yo+CFSnkAhTkR9qGStjsmu+/GwOM4VRODYpfo7fupKor0D2XJDjXb952nJEQqz2oRSB7nKYzsSsTXjt6DWjgaQGClACgfYfHFi8y7Tp4swMZKWSjDr/z9GClHQuQgykccS0A1d+zctOEjnnTe8R6Iu1xBiwSyv2jYH2Ex73i9Q6ry/VSuLqwfRVwOCBgznpZUQy0cTCAQlPSb3/zmdo6IbfLylyhsht/hb5SuA+uERvvDOCWXS2bvz0/pQaH6jkRthdbsOHNfil1uF4JEAVO27ivcKNzqpOycx4PcXHzxxY3APOEJT5hLXKxykZarr766JdLLNwPPlocmyRx5qbN+jgZUy1W+Xl6eXZs5mgWpJteqEqtHEkLr7+Ty9a9//bEK40OkFP+5557bcg7dK1XY7RBVGsOOUYuBlPYnd3awpiI0OXXeEVKewnXzqiJrm3vnmJYQl2yzt5BEpoq8rB9FXA4IchhlsfyDC6TF4XOKovlYIQrFWL1ZSSINKi4z/nbNWZ32IUHX+7t7kIWUPg+QEiUGeFUkeCMPXOOIEQUsX4rb24rUMxAlf0deUj+JO13pAAYkByfOgnsjU95H23xPm6yArbzdk4K3Yj5K2zWPGhCDnBSOfJNFuYPG3N/IAw9jjkbhXST75BHBIZvkBSmxOMsZQELl5Jn3hudFviOvJB3Iu4e4OJKFVwSh4CHJ8RNkm5fH75EOc4Nsu88iFdYdymlzBCKW88H8a56Se8TfvBmeQVRYPYq4HACYzCZNnZuyP7BSQyJ4O5ADymcdCc4UqlNgeT8oY4nkStzb8o6E/NiP/VgLHfHIcGtPnWlFDnxHzlPvkZEb9eM//uNN2ed8FUQiOQR21/mOhG4GhjHwHK763dYBQm4+8IEPNGWuHxEuhsGKW60khoSC97t5xMUKNweeajcPUg5otJL2uxg692UYETgGKN/L4XgMX4pXut6z/c4zfFe/2SlYoaz9AZnj9ciJzcbF0QnICdlDXHjkyIV+Rz5yhpAxRVqMkSJqvCEhA8g1zyRZcso5b43cSOSY7CEv7k/GeBrJtE0NyLTwOpkfjjFCg6Br2yxPoGd6Nn3h3uYrcs5DxHODBPEiTREX8074y4KDrGZnqbaT63zP/COj2pXK8Nqsff0hjvopxVMTUnOvnPPkO+bgUThQt4jLAYBJo7aLCT/vaILCfESRXnrppS20Im9oeM7NKkCJMfCICQ/EGWec0UI6yTNBYoy1FavdY1O1hSgq4R1elb6mA6NMafdIgrudcSkBQNnyuIzlUi2LnLXiGcJKDmhEAq2M1WryHG3SzzngcApCYNddd10zbgyh93vGM57RajBRxhS72k4vfelL2+qdp0pIjRK/5ppr2vcYhOc+97nHDseTq3P55Zc3IyanB7Gz8pakrw8f9ahH7bkPCjvNoAqpmFfCJ87eUaqBcTZuCMVFF13UZI5cW4z1IW9yZIxOP/30NieS1G28brjhhnY4rfFMxVjfdR8kJrtDkZpbbrmlyRwi61nmxBBki0dIOYlZx0AgDuaXfK3LLrus7VYln7xDdAiC5n2nNkp4tjlw6623trAVomP+65MLLrjgWO0tIWAySj/08xXxs9AIEDUFW5X7R4KQPnNKu/SvTSzkOaVADjPKCq4IJpkVPda+7GnQkK3YJjIBZ2yKtOwdxkPY5OMf/3hLHLRyYgyf9rSnNQWwSs8Lb4tVqXGk3D2vz//gBUBYKCvKbcoLQnnHm5FVq5Upj42/9SuulAO4z33u05Qto/3MZz6zrX4ZcnlTOQV5N6DU1WWiVL0LI5IzyTwbyfKc3jM0Bu54K2pu/+T8fOxjH2urUQUmU5QyO0uy6swOPH2rD/RdikSaf/IakBe5F76bE9wlj+aYDIRrnZ4XpCvJqLsBefXu/YGaPBbuZ+WeE4QZfe9KPowLLx1yt9vngv5FFpAEz9HP+pHnjkzxLvDokWPjlXPgyPrznve8Y54/HrjeexxSajzpzsg+g6y/hvBcxMKp4N6dfBlnpEIfeIaFQG/4+2dp87zyFOZGDhtFTuL5C+aFm/QzgmRe8tTE20ev84wge2qZvelNb2r9Zy55hn646qqrGjlRk8z1+pWnFjlEfpA2/euahLIQKX1VxKWwKxAihsXKuS+ytwxMbJNdgqP6NsNJU1gOlJQVDxeycZFsx5XrDCiGj6F97GMf2wzkqor5WQVSQMaR65ji6cMnDL4V1DzPBEVNWTHGvs8wua/VH+XHO5dtzDmJmuFCAnyH8WL4XetZY1tUFwU5tXLVBvehSMm8Va93JMPCR1PudH2PcFiZ+p5xsNp0PWWurVbnZ511VjOGIXfeg6J2HAZDxFvDGCQEkdASQ2mF7d15fRSc9DNjgkQmodnz1pWDk3ADGdwNGMScOB/oR4aRrkm+kj7xe/2gDz3XHBjzQiwKhMB9GVfeNePlGYir3+XQP3KV8+JSOBMJiLdkuAjze3pTqJTxDdF1X/JhbIytsfLdbHtGnrJLT76L0A4ZZOx5LvaSf4IAIPXa5lm8PsiR/nRvZ+DNKsdB9nKOnHvc4x73OEY4tA95tXCygDIX5f24H7JDrsmI90tOGptC5pE6ddC0wXff8pa3tPt7jnc/CijisgIwLAwDoSJMFOuyMOGsypOEWdgbjIEVKGVAuQUmvBWaUIPYOoWyKuJC4c1b5aXmShT+GKH4f9u7k5fLrqoN4O9U/wInTnQiKCjqQCciIpRdsCFGScpeo2JKRDEDFbEBWyLYpDQSY4NGo8aKHYlJVIxiB4IDG+wGDhyoYDNwLr8tT33nO5xz77n37nvrvVXrgctbdZtz9tl77bWevdbaa+dAUUQocW/vIQqUu91AQ6MWMBjkyupRf/itFS1DhBz7/aZIXSbt1g5k4JZbbmlGjJfQkRTj3VFDUO5+IxES8UJyJAszkIyF/BlHdAgbWekj8D73fUnKvGfAWCrMiLQZv3h7coYLjwrPyjvf+c7Wd8JNDntFlux0mdtquw8kGdUz7ANW5GMgbwjArkAqkleCTBqjyOw62UZkfHeOJPscAdFW149XhKE29rzPvDnj8I5707nZVYQYkG3G3jXGck1eXXOdB1t7XE9bPDc5pEMsClR4F8oh2+ugvQiIhRGy4/mQEV5fZDIkNEVYM6eQFOTW4tXCxMtn5sjZs2dbCFXysB196xKNLzcUcdkDTIrnP//5TbC5Tz/4wQ82trwUhBYzt/qvAl6XDyjBdV6zFLwiA1lZjsHAMsLc4JQz486LQClynYunTyUdIg8ULiOAqFnV3XHHHY1wOA9sG+ISMB4M8c0339xWvhIZeU6sylflETAKVrG8CJ6BYZAf47ljCP2NYk6YTU6S3BmeF6DEeWISvhjDal+4TLhI/+kf/Yz8eVmp8koU1mMJSRnD+CEX/hrDsV7LOXPGyGKNN0LYiEwIldOhvBFTiaeuh+jeeOONzaiTaZ46Bh2JGdc18h5SveQkZe1FdIVukAT/txX6ve99b2vvkm3+SRj3XCE65Nt8EeLULzwvFlTxFPIGJww8RBYeZDUlDK7EDRtFXPaAMOa5CqhzSKhAkhW3oUlY5fz7IOdbUQjGJdsvvU+JWcHsO9eBAubd4FmgDFNMLu5s7/MgUJDaRA7sshhD+8XvERDExTUQZB4+qzi/kYSLqOSEdZ4Fz0amyJiVnVWeleRcxdIliBETe7citUIUOnJYKu/HKtICmSsJV8WoRRl7Vtcbj8s4v2BdvsHQk7XqOoeAsVEB+xgPfySjCJ8xiV5DAIxPwh/CVTwJZNj4kw/vv+td72qfIdaSd4dJrclZ4U3jXeNdYJzNBzJ1/vz5lkuFrJMJY5YdZuRXSBKRQGiFGM0Dv9MO9xyGjBDVu+66q+mDVQcWuq4FJ9kWXubV85vrrrvu4o6kpaQh3tOhLch7nieHBg8rVVu8JscmIMO7zNfLBUVc9oRNy0HHy5LquCZgkZZ+oDCsehJKYLh5BihCXgqJeFZES1Zh24KhooiQDO52W0cTjwcKl6IWzqKg5irk5uBQnge/RU54LnggrNpsdeaKRlyQFvezs8F35SAIqfBwcFknV2BMrt1frN3K1bUYBd+jrOOx8BvX0273tIL0f7KbSqWeU9GwuRwtcu/62S5tdcw48P74LUOJoGWHFSPI8MRAJvzg30iYv4jZmDD5Ptd7tt7moFXPlbohMQoIoO9lx0bv0u45FHVufE8zhAD1DflLqMW4ZWcPeUYmzC3zSf+RNXIdz2C27w69CTHgroPYyXfhCUTMLTJ4XxAhCzoGPgnq7iOPJNukXdf4uh6Z8hrLgjYiNDx0Qw8O+cxiE4TWyD/ZttDwfdfTB4iV0DLCto6cz4GXUP+QcfJgXnrPs5t7Pktysb4m656Vh1J4lQybw3PwXXPIvEilbLk0lwMuKXHJwYMEZluXF6VF2SQ5cJUQhaUSevdbF+NMjYG0b5/VP60ITARuchN0fNZGoQ/0LQLD+2EyM7JWv4fII2J8hXPs7rCtUUKqZMkk+FEylGXO1VqXpAsMvZ0H2SXDo2N1SMFbsVJsch6sPilDBMdLci8D417uP87vIPuSERNT12dkMnkjXv6PGCFgkl0pdHLs+p4t9SoQcEp4qo8ZCcqaAXBtz2w8kAlhINcS/nGNhBuQM8qbAXLdJCd7D3nTv+M8Jc/O63TmzJlmhHw/1YNzfXNdsvaFCxfacyFcnnsuZLctGOfL6dgOY5jk0pT5Z/DpTfOLnNktxpDqz4Q6VulT8oiIkAGG3fjZdWYOefmtHCdkyGdkwpiZP36TYwbMd/canjXk364pTDPMBfMbRMGCwDMJ3yD9SaJmZ8iX5wOJ3vTIXNmCdeAZdS1tQdK0i0cYudOP+gqB14/mAyLoubWLF4jHFiGf87743DggfRZq5lURlw6glCgfCstrG+ZKaRl0Cg17Xufq930rNopqXUzbNRkTQkwh75IDsAoE02Sx0jRx9rnqL/xvq7l+fsc73tEUwbYrpm0guVAYhVJBWihZBhcoIG3jhn/Vq141uZVzCpQ82bEKcz3kBemI+/7FL35xM9ZWvbfddlvbIkxBenarZB6+cTJvPCa2Tw93h1DSDNS5c+ca4bAiZlBS6p/S5TEKEJecszWVyGhueR8B0R+8Isq/W3VSyiEYVrvaxPgJpVlF8mAJ8Zmn3vOMPEsM43iuJglYHgQDp//1D09b5hzSYleLMII+ZJSE6xC02tG3GvrbrhlyZ8yQ5ciOcfPSjxJsyRuyvIoM+p3xIdc8NjwkxsbYIprCTbyXDDOZFxpCMtzHPCIziE+8mUMYZ4YfmRq2QfvMFUnH2ueamZuQHJRAWMdzS0DfBp6FDPPoIDCeMR5E9yGXvDDmCBKmvg17qe1f/OIXWy5PQqBTMJ/IMq+UMTGHLhccnLjkjAkrNCsgrBmbxC4xUMpiSV5I4qYEl4uaMqJUU6yN0A89KnFpW41yMVrxSFSkhIel07Oqw6wJLlbuc6tOeQVevVdg3K45Xyanjhb2h2wRvhQEMbLEgFrJJcGUzJF/q3wKLavKIawe5QCQY4o1XjnfQxCQEF4PRjmeFbKKlCgGZp6RaYYAaU/CanbegO8y5u4xtbUSgTeXcgKwVWjmb06eDvSzdnqmuZ1aMVAICEPAmFhBm//eNy8YEytGHhHzPErYXNRWilu7KOjsJNG2IfQpoqXPeKG0V7voCn2R0AIPjJfrGY9NctSuZBhH/aioIsKQMI6dPuYZYmq85JENE6h9hrj6zL8j0yHKxo2XDNlgiP0OqSXXZCJyw6sQ0O3yZHgYQv79jiwZewR3CkiIeacN5o728FDMbZCwCJkiRgH5RUyQD/N27JlxbfLrfmwhMu6+vI5sE9Kmr6KvXIf+0F/61mfmLbLIazMGcmcu6C+kclVbjw0HJS7Zq4+5WqXpfOTDYBhk/wau3jmjkmS6JGDlACxKlnI0+D438ITWvylauxW4r7kWfYewU3JWcJRXzgECgkCBKoBFIAiNlSDvC4VmwvQ4n8J1XQdjl6m+dIVdOF4kr4IiQUQoP25hRpnB5HmjuKZChZQgGaXEyUri8zG6qWHCo2iFlgM5s2Jj4BnvJAQzCmR5GMKhTBEF5Gcqfu5a2ofgeBbzxoF25t942797M2bCXnPeSt/xHEhEQg7mpedB6Bk8BEsb9ZHnk5OkDQhgwmzmEIMlLKFtY7JByevz5Fwk5ymFxSCeOImj9JTP62ywZYickWFjyLiSb/pVv5ITcsB4D3V7xh6xJp/kfwhyKrxqDHhwXJsBdj+ygCRFlgOyQd6Hsk1WkXRjOldXK23JbiEy5brDMNMQyNGqkB8bw5b5a+6OowH6QRs9h3lp0YH8+39qxFjIWiQg62we0mVuIHpk2bPwRE2Fi8g8oui5jMeqmjPHhoMSF4JJaXBxcY/p9FRI5JrFzgkogR8mf41hNcXLoryzxC2KKvF8ZMjvCK9VKAGnyJEW7jVK37UpWV4fghBD4RoYL3LDM0N5Z/L5t/fdS2yTIt5VoREok1kxIYJYuDIQwupFoSDOS5Dckjkw5F5jJPGRkvdaBfL9rGc9a1F7gKEZG5ttwMDwcCBydIT/U+xDrxPDaE7LAxtDP66qqaGvheB4NeeApNAB6roUtgdDzfB6rQNdTcd6zQFZmcvNIK8IqdcqkKMl8j8EgrwL6Pd1/cDurJtDiAtbyavkeABQagOQfDaM7LJJw0VI8se8LjccnLhgjrwklBMhokh0uvMohI24zNRAwTSn3MsJ5SAdKQYkborJc7mL3wvvWH1ShEgJD4/PuJkxbuXdkRkxf4lOBMLvKU2xWdfm/cFo1bfQZqRFQqOiVZg7Qds1WVfbxdAlsNUJo4XC/4WOystRKPwPqXyNCFl4y4WxYE+tI38RenZkauFyOeKgxIUbF2Pkhk0SIm9DtiDyavC6+Hyu2izSwtuCWGRbqBhoTttEfJASXpKUu8ZKXZd3h+uM+054SUiI98ZfREd7/I4rPaeVIjoIjWx1yV+uxSuzK7BjbkieFquJUtSFwuZlBFYBAbLIsBgR7ze/C4VjQ44Iye5HaQxsUOoS8do4XFF6xLAOzOWMgxIXHg9KBCnhBuaW5blAHhCPHP29qsCOz1zDTiJM1KD5revIR+E6lIuSLdJewlCYKrLkuxQakpNy1dxwCEu2VmuP3yWBE9vNmS45qE6IZ1yRcRNwjfIs1S6iQmE/oE/kOqjgK94vz6JQODak1hKbkZ2zWZSD9yyAc0zGlYCDEheEADEZkpIMis5fsi3VYLnGeNdAKtXm9NiAK01SE3LSaw+76/HADIkL4oOY8RYFPDe+N5XcFddePEeFQmE/SOLm1M6LQuHYwG6MwSaehgMWOQ2kgSBW+0RVzt0Ccm/GxbTUiJD8K+yUMBfShMjw9owhpMVzVCGiQqFQKFwO4FCQE2ob9j5Ds5c9ceHNsBOjZ+zPFrbx7g7JxNzRcmlyAJlB5OnhedEOrmqhoRygt6tbT9hKcrE8nJ579HO+TU7r7Xlastwi/SFMKPl5XfXipdBmydoIpXHYtprlGKmLYixtaewpR7bYm+AJmfYqhJe8rchbL6Syr9UUuejZFxIOk4dGLnr0hUWDsZOXph969oU8Ojl7+oJcZHfkLqA3zDsv4WPzuhfoIYsrc4O3t9fYmXc5MTpVanucsq0vpAMIy9MRjKDr9ljoMazqzKQveowd6Auypt22VffSbWTMxhV9IkzUU455R+gK/eC160GjqfG06iiCHjgocckhb8MB5Z2gvCkYE3adYFJohFgui5AN403h8WowMgRnGEaSp4JoMPAE1neGn7ufa606F0j7hILiSTG44+8zEooMeb6EwihOScfaRqi5+Gw17ZHT4h76i/FT52Lb6o1TMPFcl1DbqsuQ9IJTiREiSk5f9Ci1ry/IgJ1jCEt2lPWA7H1FDo1/6jr0wmc/+9nmdXNNiXc9zqbSF1zGxk9SuSJWvWC3nZ11iKftmOZVL9hVqJ6NrZuOMOhRpZouMHbmn1wXxb56AUmmpPWFhH/1S3YFHYHYGzs6SW2nXlDo0PghQ5I4e40dHWTHJWJklyjd3IMU6Qv9kNIBtqj3KgZIT5jX+kItlh5jB/SmjSNIuErRvY5tYX/IMAKDEO26TXsIhEibLXzJxa4Hf7IZSp1o8z5xUOKic1Iky6RnbBgxq7gYyiSrElhEwfeQDTAhJMmqgCiz2rZn1zApTRzlmbF/eS45XIugM5LyW9zLdwyW3BLGCIkyWDkHwu8YU79FiqyqkCp75RkFCmV4em0wdf6ItqWiJxKD1Nj+3UMpy/WxyrG1XJ/2rD2hv7WRcmagepEAoJgZaNfUFz28OTnG4cMf/vDFCrK9jBSZMP4hcT37wg47MkhxMtY9Vn76gtwhAqrL9pQLMk8pmxuMtUqevaBkgQUFcq8vdl35gaR8c8S1kbiefUHH0A30DkLboy/oCM9tDBnVnu2lh2699daL1YLtsuoBc4NXRFVbBx2uK8q2FFbsdC0b4HoSrHvtOKPbbrrpprYgY6zX1YBZCjqIt4HOoNt6lbhwXWSAPeotx+yeemipor2rHLPlFiBs7D5xUOKCJDBUDDgPiMq3VoeIAiJBUClbRML3KGDfe+tb39qEwdbpN77xjU1pmNjIiN+95z3vabt8KD5ERcEfEzTJuMiQjGsDzxgrIEfATIqcNcF4MKhWZn5vAHIUu1U8QkQQMWmDfRpyU/SblXrPle++YSeVyZGk7NMOMkQerCz3dVZVT+hX84w8rzu36zQhVa7phmOQCzoByUJcjqEGE32aAn+9wqj7BllGkqcWiqcRFtw8TuzIMcgw8HC+//3vbzb1mA5gPChxQSqwZ0XdPvWpTzXXJfKSbcnYOlJh5TkUVC4yyjj71sU6MVrX427nEhanY8gZcSXLKZUUiKMUFXrzOwm0OU4emUGUchJvrm1PPBKE5Vq18bYwWjk3ZZdt0L2Q/fvchr1itIcArxuCaryPYXKTJ6tgMngs22kpUIc0HouBAosHq2xe1RxlcJpB4WurkIZcidMO7bUANP+WnDp+qUE3WHyac+T5WIiLRTd7c8iDW3cBQstTFntyLDgocdE5CABXvhiYThM6QBasELntxEkpLt+NZ4WbEAnJmRVevo/IpHQ/ooExIiyUIHIRYbciynWxYWEpREiJcKt/iZFRlgyqa/DOaB+XVw4JU7jOZNrk/BL38fvehjqrkR7l1qeunXb33qqNXPbIaxlDe5OA2SPMELhWz+sNgTgbP7K6axXmIHKxpNz6ptBGMryPFfA+zunKOUh0SG9y73r7WDCkj3sbPjJs4dUb+jhtziniPWA+mx9evcFAI3JsUa95B8ZsH6RQXyCcbFxvL6px63lN19NW8mbu9ezfIQ6+qyghAqcyS0pEXAhQ2PUQBEx+Cg/NGISEW9lqhws0cWGu0ClQMjw6Jq+cE2QJGRmvlrQPYdE+3hihJcTHAVWbrqwInFWZdlqZ9TRQ+0TObLF62AfJ6I2QXPk4iMCxHCYmLMkDSYkeg/cp88B8PYbVGZmgRMlFzwTzfYFuoHt67orbN+gK5MIikM44Bk+DvrUxAFnukRC/b7BVFs303Gk/d4hekD8lUqFv2b99eMsu2XZog8ENT6FklbgpctJudtQsIQV+o8pgvAqrkCMClnx3CgYxoSgeF898DFVyPTeCl1N5jwHaKTyS1d8xgGwh3GTrGBQ+eaDsJcz33Kq7L1gICfvKZzsGmaAfeMrkSRzDAgeQlec85zlNX1igHUOYL2fQHYuuYEckrMNpl4sQF7LAbrJ3+9Btl4y4hKzs8lAJGy2dLGF+S78fV/O28HvKqEddg0Pi2NodOTiG1dMQx6Dkh9C/2owIHINsZJfgsSDe6GMwpgFdwYNhsXMsuSgWCseQUB3o42NY8IK2HkKGL/sCdIVCoQ8QgdO+4iscHsjssZHwwm6Q+gDJ9zw0YS3isiWsOg2e7dzZ9SRcYVW6ZBCFjlzDlm+JwJiq1aGXa/VOihWSyBEEqW5o1Zyte5saJIliqQhMae1rReA+dptot361Utokadhzj6/hueVppM5PLxjT3Et9FtBWfby06mfkyvbrhJFcg2ztUy7cjxynf+RabJKEHuSgUq947nrC9b3InvHUfn1j3iwpUJbf52yX4Sn08QLzHvRMQHY/czynzmcHhz5emtBqjIxP5CIy7O8+zjrTL/pHH7v3sF/W3c8z+p3X1GG5eXby3LuPzTt/ga6IXCz5vXb7fc6WMzb6ODq9t3F2L32Uc33o0U02LxgjuoYNgUQfjFPPROkpqGGkn/VxaqAtlePIBl3pd9lJuIkNKuKyJSghlXvvu+++kz/+8Y9tR5PKufJtloS/Uvn2C1/4Qquua4LZlqYYkmS33iuYnCGhkqit43Z12ZmlvRK+Ni0E51qK3yWxeh+7WEDxJQnS2k3RifXqp6X9QymYZIq9OR+K0pVzpCqpPI2eoQRjamu+qpwKJGqvvBAFvySZL5ELxkJi2yc/+clWiVPyrjwpeVn+3ZsgkgvF9dzPfRlCbb322mu3ymPJMReKGFJIvZMJ9THDcvfddzeZMA/NOzkW7rVELhgoFYDN3RS3BLLgmV/0ohe1ZNOesXlznEzoY9c1z6+++uqLRmYdGCiFvW655Zb2zHIIFFmUQL+PRQOZuP/++9ucMZ765ZWvfGVLzl4XkjXfjI3fTx22Z6zsFBVi6lUWnxG30UMVXwUHkRUJuHawLt2xpn+/853vtPkL2kdPeO0j5Khv9RP7AfQoWba7dgnIAb2mJAgy65np4Ze+9KV7T5T+0pe+1OyIvn37299+kYiuA8Ji7tkgo8yIdmoved5kl14Rly1gIhPwO++8s5EXJMBkVqQOJCepVTIHytfv1IkhAKp7GnQVgG2/VnNmbnfUNqD0VAy+/fbb2z1Uu6S8CZ7zSyjqTSrNarvn/9znPtcElhLqTVy0jyLRx4Rc1WOkw+pCf585c2alxyQrKIqBkVPWWj9bFShqaAu9YoYSIXuRRH38rW99qxkok9K9Uqn5Na95TSME62LrlO5HPvKRdpaKFQ2Fqb1eih8iMb0SphEAyv7zn/98UyZIIiNKLmzrRLg22W5PzsjGbbfd1oo3+v0NN9zQpa3DNhtPpBmhRZRU8yXXDIwjDlZ5BcgFQugZjdXw5HZz0DxGKuzs6aX4f/SjH7X2MqpkV9sUuLRwOXv2bFuorPJMkXnyy0BpN7lQqdbr1a9+dSvf0HMbrmMoyIPjOXK6vXlu/kiAt4tz1UJHJV26LeMzBiNrY4ZFUw/iok/JHfJtXpNjfWwRgTip+bWqpIE28n6oNq2umGcGeoGu95m5l4ruu8I8oRPotgceeOBiXTFyTDZtT0ac52QinvoLFy6c3HXXXU0mwDNrLw+IebDKBm0L93U/8mjOabs+nvKsjcHuIIX0g/HSr/rUIvj1r399W5wtlYciLlvApP7qV7/a2K5VsG3dJovBpIRSZG0OBpDAEjwrPqsYRtaqjGAwFoS3V8Ez99M2Qk5Y3I8BzTlKSBKWvyS51erg3nvvbZOOkWVYrWp6giLRn/qHAkQC3IcC1ef+zWtie/nc5KYcPTfi4hr+ncJ3rodkWvlR+LvWEIlbnVy4FzJg9WRCe47vfe97bTsj2VhFXChayt73GU3Ki5JyPUZDO73Xi7i4n/7Uz9nqrI+RLUaW/C0lLiHH3/zmN5ucUaC9awzFO3TPPfc0wk1p8uoguBR+PBneWxXOYPj1J3I1BFmiON2H/OwKY0cueB7MGTJoC7x2uzdZUUcqocQ5UPIMKgKfPqXseYzIBBnuQVxC6siE+U0WkSL96n4IY8pWrCIuZIhe8ZoiLsaQHlpi7NbBHKOTFBbVx/o7oSEykgNolcKYC7Vqi4WB/uUtonsRV8TQsTIIDE+I+duDuGgjGc6RHzyF+snijJ5mT9iVOZnwXaTB4pEO5hnSXnoN6fz617/edk4lnNgL5rT7JUrg/9q5ZK4YJ3JMP3jubMzRF/QdfS5qsfSspCIuW+ArX/lKU0YMIe8INxfFwqOBUSprvwoG3WARAt4Z1XgpjI9//ONN8EwggtiLuGDyVn0mJYHmomYAb7755tYWBgyBWnWAYFYlDJrnJ3wElusvMeVecE3GiCeAktMu/aSdPBGUjIPSKOtVqxLGwXVyHhAlnAnkGpSSsduVuCCdVplkwkrKBORhYaAoU33lfUUQV4VftNdqD4lgIJxJ4hof/ehH22fIFgPS6yRwfcNdTS5e+9rXtv7RxwyBNiOk3O1L4HcMm4rYyNo+4uuUnLEzx4wjLx9F5xkofQRP/yACc96S5LcYM0YICaTcU1qBN4Ey7uEJyMnJ2qtPyRmPhfeQXO+RY4RxlUfACtczmm/XXXdda7N5wGMk9IQg9ELCPCHPQoYMOYPKo8GYC3+uOpiQXmSIcjAgIpPcEbJtwaEvevQx3WNuOYdJfyOGdJv3LQ71PcJhXI3zFHGhYxI21DY1vHh0HSVDR5Ar3rEeJ1/rD6QZadXXdMIrXvGK1j88XPQIUuP+kcupZ6ZXyA5SxbvCY+6aFtSeBSFGaHoRF31rYXLHHXe0s420YRPiSY/5Pbmim3mO9ac+QDCRMPauiMsekYQ1Qo6kMKAZmKHreQ5Wpwaem8xK3KQizNynJo/rIBS9TgGNUjdpKRyTG8tnmHzGKKomvIq4UEJWYcJDrtVjRToHrl9GVZ9SdLxB586daytABI+w+7fJObfyY5SMj/5FFhQho0ytSngEEJcYsF3hOtqjXRQTxe3AMrLgPYSGC5vLehWMzQte8ILWTs+m/cit98lHbxh3coZkuJ8+ojit2Hy2CSFl2Lyswii0fRAXYycMRxb1rxAlbyHlrM3mJeKfMvFTMG8ZZgSIQXYddUiSP4R08tj0SCo2z5EOfeKa2sogMYI+M7bIHsLI2M4BwTEfyLq5wOj7DXLrb88Ty8mvOcGrSS9ZMAhxIoMWEvQTcrgKCKWFl9wFegLJYlDNAURYeAz56bFl1vVDjowdoiUERa5zmC59Sm8Y3ykiwGNK5/jLo6WP5dHpV4u+noi3XbtSD0mfuD8ywohre46wmTqwMh4XOkE/IwDkhzx43xghtOSul2wg2xatbMCmpAXIDF3oObVTiBOhdE32BAlDipeiiMsWiNGm3Cg/k5ryNDEoVYqJEp1z6fu9V3bkuA5jxxtC+VMcU0lt24KgZ8dI9ti7Z45WMGGnXLpDEFZGTbuTEJgktt4g5ITYxNaH7mVyZicQ47Nu8uhbBsxKxHf9m/GgECgG8Cw93NXZ0aAP/RtpSk0L/ZzPtXsVPJ++RVi01Sqba1W/I5uUfc9zcSIXkBPVrdKsAnlNGEyKlCGaC72QcySA0qXcyHF2vvSGPiQb2o3QUnzaq18YxZwE7f9zhNZYCMciDggn4+a6jJ75h7zNrcw3RfKsjLu2Utja7dr+et9qf44get/zGH8y5VmF9fSteWChg8T0rEnCc2b8stsj1U/NP+0mE4zvKpAj8y2ykLwTRlgeA3nqlVdmwcVYp8BnjLjrW5yRFzKur+fmOh2OPCApjD5PlnaTDbrSwkHbexAtY0r+yEV2DepjOti/s1MouSNTMA76Vj/TMf7vL3kOAaPjei52yBu9hOgj4BYKCMdS6P/oR/NL++k6bZbnuekisojLBiBIBCMCRWAM6LC+hYlCYHxvk1wEhs5g7rtOBnf4NhnynoXi5V0yMbLbZx8GysTVh3OGnpAzkib33M6EnItltQiuRekiWxSUfpCYu4+zULZFwhUUGePAU2NFbrVINry/70JUlH8SU5FwHrlVidfGgvfKePidFSuPFkLTG9naTvnpq+QsGEN9g+gyPHMkPKtzZIGMeVmZkguywtB5j9erVygjMH+0U3vT9myfn5tDPtM27TXnhBMQl+T28Jj6a3x6yLH2IEkJ9UW3pb3eo9/otlUYFiHj7TDfPAPvkPnY8zgDRIsnDlLhnH5DRBGSJbrO2PMuIVtIllANDxfDTKZ5QPVzj2TtnK+3asGUEgVz39GvPELaaKwsLryn7ULNfm/umpu9QC/xXpsjiAtilN1Qm8IYkSvXtFgwNza1e0VcNkC8DpTblFARSEyd0KSOxxQopGH9iKDH6n8VTOxt455+JxfHpLAKFOe8VNDHVlmUKFfrKgMT4+A3VgnZQouEiQ2vitVfKpANblXPp/3ICiVhdUlpWGkfAlklzSFb7HmxEAe7iChU+V6ZI5Hp01BRNZ46BIeiJ9MhgmSCl4+cILT7PFxzKYbERvsYIv2MGNAxyW+5/vrr24KiB9GKx2VXxEDLEWFYtRk50Oc9F2epGTTEkBwulbvIqlW/vk44Lx6nEInTIMe8SeYafWCRgMzyzKbP9wFzQTg56HEALznYplYUFHHZEOvCCylUtGowrBDG7lYrEoLYM0Q0hnZbGbvXpu7l4XlNl7p6Koaew/6WKGskQIxdfo4cCF6B5z73uW1VfRorfvJ6UPIf+MAH2mpVsp0thJSUZ3/Tm950kHbEDT0HqzuJ5BSnPBEr/2FuSIjPaTmHKaXehQWQE/JjtwnYKWG7sVWs5HP9zDicJmiTbbm8COQCCedBZFCyK2NXCLPw3qxaeC2BcTfv5LdY7PF+SDY/jQegZrs5D4sQI0+WsEhyoSzS7FbjHTgNx4qQY54PdXW092Mf+9jFoxcgHqjLGUVcNkDipgkBxXVNQXsx6Iwhd+gqJcLtj8EOY5CpjJkciZ7kIO5ecI91rFxbEn8NATvkSiMrprl7MjiUCCO0rp8oI+EWO76stB1sKE4r8dk49MhliFt912tJ2POy4kshQuAO1h/e39WgzIFMpKolN7CVp8Q+2f9z42DFL7dFKCu7k4yH1arr2UHwtre9rSVMMoi77nAYykVW2vFKaDt5MPdWkdGMlZ1ZXtlenDBtwsFLkuw3gT5iwLUzfb0O2ql9XOqeW/8h3P4vnKF/eVwsgixGdiUu+sa8IndkgCxqt/AbY5hKp0t0k370G781LkmS7x3qlHsinEMO4nHgKTFneAOXjCNPluRQBEbehV1F8qT0LR0tXMpba0fXrsRlnW4Dn62rROs62k0+1H2yYKDrzEPyYBwvtcdwDpH/4RzeFEVcNkDcy2KhBNjEoLi5EoVP/N/nJpPJalAYG4JkUnHn+oywUZomC2XvtxRPXLTIT8+VidUDw8Hb4h48O4TeipkyohAJOQHKdmGfpY5H3NOHAsVsm7IVDwNKoVBE2qTdDJN+TploikoGvZdn8Zkx8V1hDMRFol22SvpcfydpcpOKjVOgjLU3CYyUpbYiAfqbohpWvU1IkVJMTonPUq+DovTM+t81EATjsk0seBXIKJnkhdJP2uK+5NH9tDlbxfUxI0Sek+hsbDyrtjNSXuQ8yaa8F/reLo8eW7jdUz8z2PoXEaCgsw3a8wxPKGZ09R0DwGha9admh7+eRd/7nuul3UhMj4RX406+9I8QjFCUOcgg6qvIRfIw9Kex0IdkUjsslMgr3ZO+1efDPLu8esA4ZSeLtshjQ2B4TtzT/BkSpOwyItN+q9+01f/NMXPQe0iw5+ztrSWLZNR1jalxFFZNrqGx55UgE/rImEdX6Fd97LlSc4auoy/1uzFAHvU3OeqRt0WGs+jSN+4rnObf+ssc1C59qS3Gm3ymDlVkgfwoWaD/JZT7LJ4WekKCfa+yCZsg5NHczNiTGXMgsuFZzAd6jucw36vKuXsGt6wVicF53/ve1xSiCWMwrJTjLo8iEn80OcT/bYdEBrL9kUIgvCYHwUvlTtsQe0FeBE8D4+QesuYZeEoUWTHxTSYw+e2pZ3CsOlTVlVMxt4pNRntPMDKqoApB6FMGUB0aqwkERlsY3CjBFM3yHf1q54JEQBNDwhqCmHM8XM9qVbt9x6TflbiYdK4jHKWtjD8Coi8pPApbGCX3MdZydBAzZMcxBmSCMpXM6FkYY/2QyrCUpmfbta1DuL6QiRwE7nB/KWptZpyGyeXk2zP5zLNmBc2tnnNHINVzs/OH8uyV2MhI8ZYpNqafhNDMPVsqLQB4h4YVR42/EvnG+pprrmnbXI0NOdH/jCmFqn8ZD0bNWCE/PWoouTay7FqIc9pMbyBPSQpNsUr9qBaHPkwOFiOagpQMm5AWOfZs+hTJsMjplfDqOsaVXCIs5qD+NG8QfUUbyUxgbpFXxkcfyxkLcUEe6MDsCtzH4gcxzGLE/KHjjCG9Rq+aLznSBFGk84SFzD1F5ejanL6sP81Z3/F97c9ZWOZDjy3yxksfkjHjTPbOnz/f5gu50E/Z5k7HISZ0mAUy+RbaJE/mGDlGLPU//e156Udk3Pd2rU+1DfSX52JjPA95ULvIc9EF5JgOMd/obfLjL0/XJseDFHHZAmLfCICBSX0UA0aBqOtC2UAqwDK4BpMCt/okeKmRQPCsEBhWpMXvKeeeHhfXck3KXR0MEwG0mYBj51HUCJYJS7F7UQraPVc4zYTvfZAexUNZUywUuTwKil4fUp6ehbHPqpiyMQ4Il0mrPZSryeNZTQzPapKkbgnSY3yQ0F542cte1q4tLKV4VQ5MpFS1Rz8CAymPglxQvBQjN7TciyhduQtIb5IGUzNoaUG4JaBUEFp1JaxO9ZX2azd3OeUZMLghZpSm9ngmcuG54+7lzRN7J/cI5Jvf/Ob2vR4hAgaR4kPEU0bfziveK+POGOjjEFptsGhgkMw181a7KdLPfOYz7bnf8IY3NJknW9poXpoPmcO7tpdBYRzNPfInb8n9yGjCEtnibnVtDFIpmYGj8BWMRATkMpgLKaVAdiyEjFNka1cw9Awk45IjQsD4klNEbKibyKh+NMeQ2ITeyLj5h/Dod6/eegLiXbjxxhtbocYUnQNjar7Qub6nz8gKjyK50LdkRpvJqvd5xVLYzTP5DsJLZnqVIiDDb3nLW05uuumm1l5tibfb4la+WEJSSBSiTt4tHrTLrjd6m+fRwpe8mJfkwnxUAgIpvxT5OElwJsfaRg7U80HSzVvyLtcQAU+VaqCHzJOlKOKyBTBDiWYGwwCZDNikzjcBElukuAg75UIoTfqUOqZsXve617WYPOVAaRo43+Xh6FEzIHAtBOQlL3lJU3YUOkVIwVMolLU2ETorDavp1MRgdMdbCk08E55S9nvP3RMUDEVMYWuPFRKSaNWj33JAYvrId1IV1/OZIJ6NYcihjFP3yGq4F4wludAuyiihFoZbG+ItITeUC+Oo7RQvpe6VthoPK16f89YgGQzDVEGqbaE97odcUHzIOG+QdkkCNcYB+fY+j4W2MASUaLxfAbmi6HkHzAXEkPz0WG1TdOTx5S9/eevDlEynpBkofRoDBdqrSB1Z0OZs0yXfjJp2uYbrkhXkhjfJv3skbed+8qmMI0NjoUJGyav+ca94trTHXLLi9n5CtGToqquuat/JVnOfe49s0Ec9QjAh9MYMkeYJIoPe92+6zNgOvTvaRl8hKD5Pv/lL7ukU16Mz9uFxcU1zgkHM8QrkmGxLWqaf9HX6RzvIPCNv3vm/sfFdY4WgIwl0OuLofSQBWeulk/WNMaaP9R9PHBlMwUz3TT/qU4Urzb8UD/XMZIZc5Wwxf+lHus/CrtfxBHMgp6kLNtxhlNpkPkcIyabvaEvsZs7JMwc9l/Ewfpt4iIq4bAGCTskResaKkjYA3vM3AmPA/J9StYrNiZ0G3GSzEiBshNFgm0jIQE/SMmyz0A+FT9lrj3ZQgEma9H8TwnNQotoVBToEQ+U7lJtnGBq4XsjOGvdGunil9F/KvA/DGBkPgu9ZjAtF4Pcmz1SBL8+KHPWsKcEDlD7WppQ2p/SGdUG0nTeJ7ERGMubkwaQ3ua2wUqcjRel6rlpdS9skfDI8Ys+IC2VJSQ7zPBifhDA8oz6eAoNBOfkug7bpqeOrYF4llMogUoRWdOQCCdC2YUjKcwh1GuvE+2PoGODkGwA58XuvKNpe0JfupQ1J3GfUvYYJ5uac+QS+nwUDeckuKC/ExXUscpaeyrsJ4gU0N3JYKOKi3cMt5GDuZ1s8Gc9nnkv7yA0ZS0HGfUA/GUeeCm3k3SITDCIZGSapejbEgGySYc9F95KV5LyQBTpd28lDwo+92m+8UwXZvOalJLfJKRx6+zyPhRqdp73DeRdPmzEg1ymiGJneJyyi3M9icbgw0UfGGnlCJMlrdJtxoDvYHnMixIWHzzNv4iEq4rIlCF4U3RwolLl6EAbaQJlcUx6BfcA9U5BtFQiR19x2UO3G7HueYD2GtpoQJucwZDEF3+OBGYezsnPkkKBITESvOaT40lS+SpIJuYMPgYRfEoKZw1KFSNZ5a/aF5CNQ5l6roH8tBqYQ2egZeptDFipejPkcjMXc/EQkGK+lZ7nsCnN8nX4DZGVqpcxghYQdAnQtA75uEYVQeY1lOVWuGeTeh8bOwVwhn3MyCmQCmZo6tJeuWaIf94E5fRAv4yo5tmjz2gVFXAqFQqFQKBwNirgUCoVCoVA4GhRxKRQKhUKhcDQo4lIoFAqFQuFoUMSlUCgUCoXC0aCIS6FQKBQKhaNBEZdCoVAoFApHgyIuhULhIlK6X9G+4QnGCmSplTEsNDVEThwfn13lejk53fu7FvGaO0n2kKeXb4r0TQrNnea2FgrHgCIuhULhIhADhtbBhQ54CxQiU1pf5dEpw6vKL6iqrMhUzjxSpVn1VZVJFYTrYbRDhiCE6DTDeT5InwqyhzxlvVC4XFHEpVAoNChz7pA5hyk6tRbpCBAWJcqdWKx665gsIDoOp1Md9oYbbmhVPZ1g7FBAZ/QgPo4y2LVKtBLjTrF2fhUy4CwqVZ73cYBfLzhsDnlR2TkH6BWBKRS2RxGXQqHQ4CRaJ/p+4hOfaMREaXRGlgfGQXDOo+HhUH6c92R4ppaDQi9cuNBIhNNg/fbvf/97O0ztnnvuaWcvLTluYhV4Wf7973+3U8BdExFApObCR6cFzvJBCB3e5ywaZ4D1Os25ULgSUcSlUCg0/OpXvzr5/ve/307OzVlcyIbD0ng5HHT55S9/uXlcnMU0PBV6CrwgzmNxeJ3rCBcFSAhC5F7yZxh374WE+O0wpwZ4W5xazovj+86lCRlyrbwQqlw/cA+ky3u5T85V8X7uk/u7V05QT3u1FbTL+77re8HU9cChkL/+9a9PPv3pT5/ceeedjdTp39Me4ioUTiuKuBQKhQahouSqPOEJTzh54QtfePKUpzylGe2f/vSnLYSEwNx+++3Ns7KOuMjpcNCea+bE7sB7v//970/++te/NhLEI/GHP/yhnRgLDvh0eNzwhGonV8u7cZK1U3/l3AR//vOfT375y1+e/OY3v2n39H/XD/lwkJ0wFs+R04NdC6FyoJ6TgnNCeu7z4x//uLWJVwfB0E73BYTOSb68SA888MDFfBskzcGPnnt4Pd8VanOSNY+Wk6wRLqcSFwqFzVHEpVAoNPASxMMgJwNZYVwZYl6Wq6++uoU5hDumTjwfQ2iJFweZ+Oc//9l+k5Nsf/azn7VwDy+O/BieFMQpHgz5Mc94xjNOrrrqqpbsy7uBcNx3333tWogQ8oQ0/O1vfzv59re/fXL33Xc3QvSLX/zi5F//+le7v889109+8pNGgtxHuInHhtcD2bn++utPHvWoR7WwGPzud79r97n//vsvekZ4nRAPkF/jWkiRdsYT4/m0DeF7xCMecbEveY+QJqcoa5/wGdK17uTlQqEwjSIuhUKhASF53OMe18JFiIst0fJeGNnHP/7xzWtw5syZ9v+hJ2QOiAOvxW9/+9tGOkJaAGFBXpAaYRxhJB4cXhlkAHFAVhAAISHQFmSCV0aOiBfSkFyaH/zgB63NPCPaKmyDSPjcfRCThz70oe195MX1eHkkDXv2EJe//OUvrc28S4AgyekBpEbisnYiNQ9/+MMbcfKsvDwSmiUgu96DH/zg9hvER14Qz47v/PznPz955CMfWcSlUNgSRVwKhUKDXUO8E7YvC8kwyEgAEsHrImz07Gc/u3kn4k3YFa6DBNltI2wj/HLrrbe2HUrCOnYkuTfjz1uBCD3oQQ9qoRjEINu3k7uCUCAFz3zmMxsRQnS0nwfGdSQOe//ee+9tHhpeFC/3nQNiI3SG7Lz73e9u39Xmxz72sSfnzp1r9/jud7/b8li0Wf/95z//+X/EBSlCpjyv7yA/hUJhOxRxKRQKDcgAb8GHPvShRhKEioRYhFd4FIR0eEqQh2uvvfbkYQ972M73FEbhUUGanvSkJzWPBY+HsBHSZCeO0EtIAMOPAPBeyD+BFLbLi3cDeRGeQRB4WIS8eIrOnj3byA1iwXuCRKyDkNWTn/zkkz/96U+NXPHEyLHx/hOf+MTWNu1FXAqFwv5RxKVQuMLBa4EwCKvwTDDEDDJy4K/QDa8CQ884C+0gGsI7wy3R24CHRw6LsI9wjP/ziCA08kp4L+SjDOGevC7IiM/8JhV7PYv2eQZeDt/N537zkIc8pF1DmMf/wTMnKXgK2iORl2dGqEkYST6LnBXtTtG9QqFwGBRxKRQKzcuhUBpyArwcQiFewkYM9De+8Y2W+Mpw88jwlKzbWbQLkJAkvs4BWUFCeIuQHTkum97DLqLhtua5+yBEyBCvj3slJ6ZQKBwWRVwKhSscjLdkXNudkROQkIoMCLf4t9AQ4y6ZVQgHcZHzsStxSY6K/JS83AdhQQyEg4bbqMFn+a7PeD54QhCYTYkLQsLzsqvnqFAoHA5FXAqFKxyMtx0/QkNCLMIm58+fb7tu5HSAcIrdMMIldtLY7SN8sisQDTkz8kfkjcinQZ6Ep1xfjZeEdABZ4QGyS8h3tGVXIGhVU6VQOB4UcSkUCi2hFUmxXdc2ZbklCARSAQgGoiBMgrTIFRkSim2BiPzjH/84+drXvtbuxYvj+AD3sV34qU99aiNTyBXvj3trh+/Jy+F98W+vTb0twbjS7b6h+FwPwlUoXKko4lIoXOFACoRK1GphxIWG7Lbh/RAaCoRiHvOYxzQyka29gYJwQjbeF75J7gkvCiPt82HJ/0DeiDCPyrTqrQgTISh2AKkZ4345QNEuJlVxVe4dlu6XoMs7g9TY/eS3En0lzLq337nukCxoj6J6dhdp89DjkmfxOdKUmjXZmYR4+FyCbs50EtKyk0mfaIvnCrQRsUpVYoRMWwuFwnYo4lIoFBoQC+XplduXhJvy+AGjLXSDjAwNM3gfUWDE4yHx/WuuuaZ5RRjqYQG6ALnxHSQAAUFIch91V4b3UdRNvRfbspPnwlOCaKjqq128Ns973vPadxEe/5Z8K19GovGwve7prxotPE6B7wmXITx5ZZu1pGV/9ZMqwu6vnU972tPa9fQBAjgs0KetcoicsaRNSI/fFwqF7VDEpVAoXES8L7wCiMCwMJvQEMOMTIwPCLQ92nlAKSiX8AsypOhbfjsGLwavyqMf/eiWa8I74b3s3hmC0efNyJbkH/7wh40kaIvQlTOAVP5FIHzX/V0TqXGt1IIBbbQrCumwY2r4PDxGyAuylbbkfZ4c5xHpgyQNu08OkfRv1x5eLwnIrqMt2smrVCgUtkMRl0KhcBEp4sbgDw8KXIeps4tch+GfChEFIRe8Jut2KCELvue0ZZVq5cLIdxHaQlRyGvUQyEVqt4yvle3N4zYDT5DX+DPtHXpnAteZ2x6tCrCQm+upi4N4JfxVKBQ2RxGXQqFwcDD+QjBCMlPelSnkfCDeHfkiPBmK5k0Rk9MEYSJhMKTFcQljQlQoFDZDEZdCoXBwJA+EQReuWbodWRhLOEjeiF1EckXG+TanDUJRT3/609t2c/k7p729hcJpx38Bh8nXBsnUc6wAAAAASUVORK5CYII="
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To compare with our studies, we can transfer the results to pullout force $P$ by evaluating\n",
"\\begin{align}\n",
"P = p_\\mathrm{b} t_\\mathrm{f} E_\\mathrm{f} \\varepsilon_\\mathrm{f}\n",
"\\end{align}\n",
"yielding for the strain 0.010"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"p_b = 100 # [mm]\n",
"t_f = 0.11 # [mm]\n",
"E_f = 230000 # [MPa]\n",
"eps_f_max = 0.01 # [-]\n",
"P_max = p_b * t_f * E_f * eps_f_max / 1000 # [kN]\n",
"P_max # [kN]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The bond-slip law reported by the authors of the paper has the following shape\n",
"<a id=\"cfrp_bond_slip\"></a>"
]
},
{
"attachments": {
"766b18c8-7f58-49a7-9406-ec2022c29188.png": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAdcAAAE9CAYAAABZWyglAAAACXBIWXMAABPmAAAT5wFzERBqAACTqElEQVR4nO3dCdxtZVn//52amiNoiqAoICAKgqCMwkFNtJxwyNJKC7WslMwJBxxARdLMObMMLXFWFNAGQSVkFoVkkEkmQcgRFZHM6fd/3/6vx/uss/a8n2dP1+f12q9znmnvtdde6/7e13yzX/x/dJIkSZIkmRg3m/YBJEmSJMmikeKaJEmSJBMmxTVJkiRJJkyKa5IkSZJMmBTXJEmSJJkwKa5JkiRJMmFSXJMkSZJkwqS4JkmSJMmESXFNkiRJkgmT4pokSZIkEybFNUmSJEkmzEKK6yc+8YnOGWecMe3DSJIkSeaI+9///p0nPvGJE3muhRPXCy+8sJycn/3sZ9M+lCRJkmSOuOlNb9rZdtttOzvttNPYz7Vw4rrlllt2Xvayl3VOOeWUzje+8Y3Oueee29l+++07m2666bQPbQO+/OUvdzbeeOPO3e9+92kfSiuXX35554YbbujssMMO0z6UVk499dTOve51r84d73jHaR/KBpx55pmdH/3oR51999132oeyATfeeGO5Px760IdO+1Baueyyy8oxum9njauuuqpz0UUXdXbeeeeZvO6+//3vl2tv66237myxxRbTPpz1cD+4Z613BGzWcN15/PznP5/I8y2cuN7iFrfoHHLIIeX/H/3oRzu/93u/13nRi17UecpTnjLdA2vBTeAG3WqrraZ9KK28+tWvLgvJ+973vmkfSiv77bdf2UjNooDttddenUsuuaRz/PHHT/tQNsAi97nPfa7zqEc9atqH0sqhhx7aufTSSzvvfe97p30oG/D2t7+9rCdvectbOvvss8+0D2cDTj/99M6ee+7ZOeCAAzovfelLp3046+F+IKpPeMITOm984xunfTgb8MpXvrLzqle9amLPt3DiOk/suuuu0z6EuWYWhWseuNWtbjWzwjrrrFu3rvPBD35wJoV11rnTne5UNsKPe9zjpn0oa0KKa5IkyYDsuOOO5ZEMz0YbbdT5r//6r2kfxpqR4pp0RTzz1re+9bQPYy5505ve1LnmmmumfRhzievu9re//bQPYy4RC+YSftaznjXtQ1l6UlyTrohXJ6Ox++67T/sQ5pYnPelJ0z6EuUXOyUte8pLcnMwAKa5JkiQLxDbbbDPtQ0g6Ka5JkiRJMnFSXJMkSZJkwqS4JkmSJMmESXFNkiRJkgmT4pokSZIkEybFNUmSJEkmTIprkiRJkkyYFNckSZIkmTAprkmSJEkyYVJck7lBr95PfOIT5f9mzM7iqLkkSRKkuCZzw5/8yZ+sjJnTO/X9739/55GPfOSUjypJkmRDUlwXgG984xud6667btqHMTaajm+55ZatPzvuuOPKIOjg+9//fhlcneKaJMkskuI657zjHe/ovPOd7+yce+650z6UsbnDHe7Q+fjHP97q7v3a177Wuf7669f73vnnn18e22+//Qa//3//93+dm9zkJp2b3exm633vda97XRHkXXbZZb3f/9///d/Oc5/73PL/zTffvPPiF7+4/H2Tn/3sZ52PfvSjncc//vGdX/ziF52//uu/7hxyyCGdTTbZZL3XefOb39y5/PLLy9cm5PzxH/9x59d+7dda3/enP/3pztFHH925613v2jnooIPK9w4++ODOM5/5zM7WW2+93u96zY985CPrzcU0vejBD35w63MnSTIdZlpcP/ShD3Wuuuqqzp577tnZe++9p304M8m///u/L4Sw4rvf/W4Rvh/+8Icb/Oz5z3/+Bt9zbRDdprgec8wxncc+9rFltuW//du/dTbddNPyfeJ9ww03dN797nevCB++853vdB71qEetZxmfc845nQMPPLDzwAc+cL3n/sM//MPOhz/84fW+JxbsNeE5Hvawh623EbD58d6e97znbfAeWOS//du/vfL1y1/+8pX/n3zyyZ3TTjttvd9/z3ve03n605++3vf++Z//ufPa17628xd/8Red29zmNhu8RpIka89MiuvFF1/cecITntC55JJLOj/+8Y87t7vd7crO3MKy8cYbT/vwkjXmDW94w4rg/tM//VOxDP/qr/6q8/Of/7xYjb/zO7+z3u9feeWV5d+zzz67CJENyHnnndf56U9/Wr6/0047rfwuq/Hwww8vorjtttt27nvf+3ZOPPHEIqD/8R//UZ5ro402Wvn9ENGa+vlOOOGEIqwPetCDOne84x07X/nKVzoXXHBB56UvfWk5bhZxIDnrqU99avn/ZpttVjaRX/rSlzpXXHFF63k45ZRTOs9+9rNXvn74wx/e+e///u8SFmDx2mQ84hGPGOSUJkmyysycuFoALZaXXXZZ5zd+4zc6O+64Y7EiLGoW1COPPHLah5isIa4Hmy1CCoLFJft3f/d3xfpktROpxz3ucSt/c8ABB3Se85znlP9/73vfK/9+4AMfKBu12972tivuXxCrr371q8Vl+5d/+Zfl77h9uVp/8IMfdN7ylrd0XvnKV7Ye293udreSVLXbbrutfI97mKC/8Y1v7NzqVrcqz0lcvTYXfi2u73rXu1Y2De973/vKBvIVr3hF59WvfnXr6/3t3/5t58Ybbyz/dy/8zd/8Teezn/1s59GPfnT5ns1nimuSzAYzJ65iSoQV97rXvYoVITMUl1566TQPLVkDbnnLW673NXEkQsGPfvSjkszE0iOuxIZbtvkcBFj8lnAee+yxnU996lPlZ7vuumtrTPfmN795yUb23He+851Xvt/tmhOPfdnLXtZZt27det9/2tOe1rnnPe9ZxI+gCm0Mgr8Bt7A4smOvYfXy5AQ2nb5XH+uZZ55ZNiIs8CRJBse6Iu9iksycuCbDIV4nrrgIEAqu2Jr//M//XO/rpzzlKRv8nd951rOetfL1r//6rxcL1Pe/9a1vdfbff/++r00Ia/dvP7bYYouScNREnFT8ti1uPAiOXay4Ka7vfe97i4s5eMYznlEeNVzY3/zmN1Nck2QIbM55S3lIJ8nMiavFRYKJnTmXn0UskLSRrA+34x/8wR9M+zAmgsxe8fXg29/+ducf/uEf+v5dU4DBouSWtSMNZN52e76b3vSmreeR+3lQeFncpKxpmx4JTPe///3LNdzMdO6GmG3bdW5T8aY3vWlFYLfbbrtiheOMM84o9w2reY899hj4eJMk+eWmXijniCOOmKjAzpy4QlYnt5uyh7p+02KZrI/z5HwtIsIDp556avm/G0Aykzhn8MIXvrCIketE6YuymBo1swQ6EIvtZtWJ6RIrGcKsTglCX/jCF0rt7aCIm0ZMVLay65U41wLfPL5AwpNsX78fz1HjOGwOQlx1qGI5/8///E/ZXNgcyGyuS4+SJOmPe0YYh1G30OJqoXzyk59c3qjd+G/+5m+Wxc7OX+xNNqdEpyYWGCUWNVdfffVaHXayCvzLv/zLyv8l6jTdu+KTxJdLt+2z/tjHPtb5rd/6rRJ3RSQ51RAosVPP8fd///edO93pTmUH+5nPfKb8PDKMB6G2uv/8z/+87+8rL/rXf/3XUh4kMcqjFwRf6Y7YkPfmUWPzoaY2SZLpM3PiyoKQrYn73e9+pZxC9qQsSvV8D33oQzu///u/v8HfWRS54GokqTTrBJP5QTOHIDJia2TXPuQhD9kgThvc/e53L80b6trRJi94wQuKVWjnetFFF5WNXeBaa3pLHEdcn01k70pGUt4zCFtttVXnqKOOWq/O1fN/8pOfbP19lunb3va2zp/+6Z+u930779e85jXrxZ2TJJkuMyeu/ZDo0SauhLUprhbBftZAMrsQOglJhx12WKu3Aqw1P1er2gZ3KxFTqtPtOZTjyEhXRxpoFrHXXntt4Gb94Ac/WFy+6rCb8LTISlZuw9Ny61vfuhwblNHUIgqZyZKQiL9aVcdx73vfuwjloYce2nqsYkOet9mhiYWeJMnsMHPiqt5QXExJgQXKLt5uHbI5xaWS5UAikHrRXojB9kp6EpPul/DlmtPMIRo69KJb4lNAjDW9aMLz0kSMmOtb7S4rWfzU+43sb6Vobcdq01Fb2EmSzB4zJ64WJ24+bfAuvPDCzmMe85jyfcX/ivB1vkmSReB3f/d3SwMM+QU6QtVtFdXiStJKkmQ+mTlxBTce95oEJu40vVp11fFvkiwKNpDCHPvtt98GPxMDHqbuNkmS2WImxRU61kgQ8UiSRUVClgz5JEkWi5kV1yRJkiSZV1JckyRJkmTCpLgmSZIkyYRJcU2SJEmSCZPiusro2FP3qzRY+z73uc8Uj2j+MSBcW8IHPOABfX/3rLPO6uyyyy7rfe+kk04qvYrb6kjb0Mgi2iFq2KDWNUlWm7judKrTXGQRaLsfF5UU11VEk3VTUizk6nf1uNVOT3efJz3pSaXtnhsnGZyXvOQlpR+vNpnOrUkx3UpWdET68pe/XG7maMzwxS9+sfQo1gfYPFhNGXrxzne+s/P2t7+9bJKgmb+pNd26Pc0qasSPPPLIsqFQPzvJMh/DNZQOXXXVVWV4QT1cIRkNjVFcd9YQbTzNFZ7HoQxf+9rXStOVyIi/4oor1pt0Zg1c1Gtm/j6tOcFibBHXDEBPZBeR9nra3WnA7sbxPR162oZ3w8208cYbr/GRzy4XXHBBaWd57bXXlq+dO5YkkW3jS1/6UpmK49/gBz/4QREDj1/84hd9xfXggw/ufPe731352qQeQ8rnTVwtcqeffnp5aF5h5uyk0IrRAol//Md/LL3Ak9ExkMGQiZ/85CdlE6gOWqexecQ6V7cVhU5kgfvPps+medFIcV0F7DZNcdFo3YUT+NrDTk5PXFbXE5/4xK7Pc5e73KX0m7XAJ50yCJx1VPPv//7vXcV1kugQZlOkb/A8WhDJ/GCONWGFSV9tfaznETOJmyMfGRhGRy4iuUpMmPPOO6+4ErnduC/b0DfZ3E5WUBMXm1gL3vrWt5bneN3rXlca03On6OqzrBgK3sRwBgPjVyMmZSKTUXQw9pDl3LR0eSgcl3F1BkcYVq7DWFubzs997nPFLfYnf/In61kirhmN+9ua77MK6+uEF8Tvx8asHnPXPHaPoN+cSjHs9773vStf86Zo5NLG17/+9fUm/9SvMwzf+973SoeqwHjJaHfaxLFtsskmnYc//OHrfd+oSZuuZl/o5vtHnHdj+6655prydZMPfOADxVI0ZavG5/+Rj3xk5WvHcde73rX1WIV/3LdvectbypQj16dN9SC43uQUBK4ZgmTUJnhemqMG99lnn84222yz3vd4a4REXv/615cRhcIi22+/fetr2uiLhe62227la2uToRI2rjvuuGNp0el5hBT0dh91rKFQGKOjH3Hsm2666XobZ+/b5/f4xz9+g79xzpybdevWlRnP+tGbo6yzX/OaWStSXCcI0bTIGiPm5jIlJXCxnnjiiWUCCjej+aO3vOUty40B7jpDsrkc99577/I9cSxuUILLbeIGcBOZmGLxm1dX0ShwBWuHCYu+pCLnmyhZgCYtroZGuLHNWgUXsoXX5iYa919yySWlJaeFGj4fx2hj5V/u18CCYVFwHfh9M2QhFuU5vM5nP/vZ9ZK0CKJpPkSoyTOe8Yyy+HmdO9zhDivftwGwiDkvHoNAoFgPRDsw7s9kIC7e2lInrCypto3OMOin/LSnPa1z7LHHrnyPq91ibvJQPUhejNjs25133rmcH4MO4H6ywRB/b4rr0Ucf3XnVq1613vfivHs+79mCrAOc+9Dn4GeGLjgG5zUSb3zuzoNe54Hj8xmYulRj88Tlbnxh/K3X0onLpjuOvRsGPNTnRKycuHHr+xye97znlXnDNUQvjo3AcCm7Nmw6gtgwGAzR3MRZYz7/+c8Xl34NUZIv4j4j0NYoIm1DO0qP90MOOaScW/eNdcy/2223XRHRGp+LOcuuB0L/Z3/2Z+X8mzAlZ8Umq96suFflV9iYiE8LvbnPwCXt8zZNaq1JcZ0QFh0fsEXDxVf3QXajszRcwMFmm21WFowDDjig3BDE0kVhEQ8rw83rBje/003mppXp6ka1KNh5u9ACyTbdRq/NMt4793cvdytLiUXgd7hnLRY2Js67+OmkseASNrt6izfEv8NFJ27k87Zgu+HD0nFTE0Nj44iz8XBg+cQNH2IMn3fEkP1OjZ13LazOkwXHYg1Wn6HsdW9iO/a4fggkgXc9tg2Thw2dYyWsxu65trw3c5BdYxa5OgFFnJuw2jja/LF4bSiHGSoP1zQR4QlwD1gUXbue28bUQhw4Hp+BDYrjinix+8Y5a87cbeKaYWWG1WShNRyEZek926w619Fq1T0Vwur5Q1h9/jwFzplkOMfIkou8CBsknzlhtSEW1gFhZHWZLdwv1u3vWYmBTaTPMDbS9bVT/01ATHxGuM1tblOey3l2zbjO2sTVNRjYABJlG0Xn3ftnDYLFL4fBc4wirmeeeWb5DLi9WeL+NdaxGZP1+fhMhIBYnj6rY445phwn71DTC+DaiI2kz8Z5t8F17NZjCYgprnOMhA43ESsqLkYcf/zxxdLxoQfcKgYTuGGMGnMhN3nlK19Z4rV+1jZmT+yPpeOCD+yK69eeF9w0FrduLk7YvcMu104WFg+4EcMSnBTEQ8YmVyBPg2Mj8BZN2O2Hu5a4hIuRQLBmuLV8r9tg9WFxzVigLRi1VdfEghWwAFi1rFKbuTZsaixuMYuW18SiykJ37Tm373nPe1Z+P+bMWvSEK+DzE8IYhjhOs5nDEmPFEA+u9Uni/qmPL1ys9XHYAAfuvcCkohBWZTFEl7CGiPq8QwzFScOCdC/aNHguGyIbkUFK8Lx3G/O4r5vHXsML5rjqjXx8PkTMSEMbLx4I7naWPs+G467L0CLU4Xlc1zaWEgVdu9YuFq1rvVuYYBjifDf/bcLydjw2BPHZ8E7xBPTCRihiuDbGNocEllESXsK1IsV1ArA47Q6JXS1uvrY7DmG1w+YKM+nHDtAuVqKMBY44cE1xxbAiLDRu7F133XXl+SyQnoMFBzc7d3FYqy5+i96iwZqJxYa4yEBEWKx2rgRi0LjWKLBA68+iHlZe7+JtenzmdtL174wLQRCT9OD28xrwedfu3MDCG+5iGxLWfm0RBeJTsMBG/a7/9ws51O/Z/4cRV5Z1WPH18xDaSeN+jHMViGESLZsnosH70e+zqs+Jf9vOj42XuCUPkk0Cy9Zib2PEQhOL7wdhI7BxvfeyEHm2WPwBd7rXhnshPBo2hjYFxNXGwKadt6KJ1/X6q8XWW2+9nmu9FzvssEPxBoVXB1z/97jHPXr+3YMf/OCV//OO+OwlmIq/p7jOIT48u6O6pIbLipspmg/YYYrjcCtyd3C/iGewjOqaQ9aRi0LiiptAprBYQzwHMbVwsyYsqmISmEd38KCI84j5gKAeeOCB6/2cuLJsV1NcB6Vfac+42KjZzAXhsm7SXPz7HZdYP2uVeDvXkZVtsSY+3ZJ3RsHxRyx7tfG+2967zQdx5WEgKu5XvOhFLyqNXprwXhAr96Bjb3PPslBtfGxiPC9smE899dRiAfr+s571rAm/w19hE8XN3Rajr2G9TgMGxDgNWIbNq1jte7EfKa4TQKKC2FeN2FAIKwTVI14nlsdtRDybxfysU2JiZ/mCF7ygxE+4TD/0oQ+VzFSxA4Lqd7hLiC8RtzuV6r5oxdgWPa4qsNrrnTqIgMVOEhk3rB3vWlDHum12Ii7pcwqL2uapDe5XruNRPiuvVbswu8EzYmG3mImH2vz1gxuOKxMshpvf/OYlAaVNWOtkmWGRQes654Gpk654H1h6vDfcqG0L8aBJWv3w2Xh4H3U8Wh5Em/XGbc5SDEvSfcca9b0a51DMT5KNDYsEJW5Y9zDvgXP52Mc+diLvoYlj4+7l6VFx4DMkuNzVcU0KpUiKqqljrqtJMwO7FzYIkakfiPUKo0UeQxv19cG1LFTns5tGv4AU1zGxgLl56h0payKsTXAVSX4hFHbGLnAuHG47C19YH2JdYYFyV3FlSOJwUYkduHFdLNzIdsayIe1UiYrFWoxB4sKgbf3mgTq22bbzZ8FztcvStJDVpR2rifNt4+Pzl537yU9+sgisTZRF1f9rEZQdqRuXOKgNgfpFx93mnhsHsbKTTz65xIEjJuf/PCFtOHaxU9egjQu3GsuSd8DGr07Cg+QgizULzeaAq60uURmUEE7JJlzpzovMX4LgNZSvxO8QI/eA1/X7NpFcnCzPUfHcxM4GNhCmiTh+E4JrweedcgxEmeeortskoGKxuoCJ+/lsNZJxj/IG+Ln7dzWJcxYZ0ZKBfD6R5MRN3vTwrJWF5zrkOm9zzxLA+jhcl9ZV3/Mz95Rr0abLOtfNArbZcd/JLHfNCCNxx7tmAl6HtkYnEq4mSYrrmPigfXjN7GAB9IBVS0Sl+bNyQ1gJgSxii2E3LCDcVgRTTEq8FlzMrIonP/nJ5Ub2fQKjHrAW9nmnziRsc/vW31MyQLhkya42PnNCL9bovNdJMrA41LWHLDXu/tgcSHSpE2cGxUKtHMUC3kZ9PiJbtReEgutXfoBrKK6vwKJWW3K8JoRPzJQVMSqeh5ixTiJJLPD+6u+5/i2mxNVGq/n7oyKGzuNj0yv3wQapiXuMxcUSdO96BE0rmhDEsbWdS5sV2a6ribXFRp7rV3yzmfzWVku9VrAkPdqwWQnL1toZuQA8KRLeeDPEoW1KfV7dEgUZKM2EuOZ7ZsXH5yi3JWqrJ3VdBSmuY8JaarqGmoumGI6do5vNv0TSLs7vWZy5EttgmbI4LHwWAhcEV12Ip59JEmDRsYo8p9cg5JHJOe+w+i3AkkLaiuCJnF26DYqFsHbFcj9yz9Wudz+P+tNBduw+LxuWNreSz8cu2ENcDW5WiRfci014H7wmzwNLUWZuLYBNt5nQQRxrHXcn0NEruRl/JvLqB1lMcgFgsWFlikuLqTbrCp0/13FkZMN5tykkOjXem+uRGx4sN+edJWnR6taooIkFj2uVCIS3gVuTRdwmALLx3SthSdc1xG2Losxcv9MrQ5cVJwPbBrlbO0v3nfPCI1DHWZ2XZr1pxFxtSJpWkDCCTNdB8gIcM2vNRqrpkreWsEZdS23uet4H2fQyfOvkIX/HU2Jj1MTPhLHqc2U9IWDR+9zzOv8sx2b9cC9cj+L/3XIDIJZaf4YsbufQ/RDhNteI55KQVdcBN3HtsHjD1e/+aCby2VDZdHhN5yqSQK3HcR9PghTXMbGDjziV2IUducWthrvLLpeVqtaNNcplRAijIUEbnstFSUQllXDX1Y0puIZdHFzHnsfuLmKy4hKSn+rfn0fczB7d4EK0oHk0scttIiY7THkMgfZow+LnucQzI0mEiNV1oTWsL1mqxMi1Qoh6xYJYvm3HKgzQ1l0IPm8bLgtwuCAJPlG1cFhYmnFpXxOZemEhmm0xY9cVr4kyD1jgLVRKKrjg9txzz67vp4Y17B5wfcfrOi/dyrHkK1g4IzM6Gq10wwZ2kOxjSUp1nXAbBFFJXd1jmpC2WaHuda5jXpQaG7xB8wEcNzFzrp2TGpsgiWfOezfXqM9GXkfdKtRn1C0pjfeCB6z+7LjLbT7EleE+I1Tcra6nQeGOtQHuFdflaao/d2sa97r7KzxCzgX3Nvd6r02x/BOufTkHkCXdjKF7PVaw99TtXp0EKa5jwOJ0I4X1wUqq+2SyaN2Qdl3KR8SOiCvXCBex//fCReL37NpdVP6eu8TFEtmzbiCLv++zdFhabhS7MK5JF3b2wl1dnPd+i33NWmQ1W5ybyV+xULbBuhj0PdgQNH+36RYflGFel0ANc54nyTBjIiNZahy6bVKI+iDnQMlKv7KVwDrTfD0esrbXGeX8D3u9dzv2QUZMYhDxtwFdbXLVHQMWI+vCrov10mwg76IifsSVe8mOUu2qHX6vjLcauzcJH2rmxKjsXCVF1a4O2YESbGL8GivEDSNOyyoY1JpIkiRJJsNCiqsMTvENorRaSFpijWpLCG64Os5iJy/OEjEOrmCxQyLcr11bE1mNYorcvOpgCa0EC6IdxfjisXaV3Geen4izjIluJAckSZIsGmHciI3P0nzshRVXSQpOelux9yRQoyoxRExBIkd0DQq4bX0vujNJ4xcDHKXeiiso+hBLJhF78lzcweF69nrirZKZxGwkYChjkQkq0Wk1i9eTJEmmhRis6otp9A/uxUKKq3iBdG7JIERm0sjC5Irl5hXPNC2inhJCDCWTRGKTui6ZhbWwsmIlPci8kzggIanXxAzp9bIrJUHJnOX2lbQgZqV3qEYKrFhZhJJXCLBm12KwsuFYs5Jgpt21JEmSZBlYSHFdbbhkxU3rdoc1XMVETXkCWI31WDDWpAJnrlvWZ/SK5dIl1t3qVCU0scjFXnV/8rtKLrioI+ORwEqZj3IGgkrsJTd5/l7N8ZMkSZLJkOI6ApKEWJLRyL1ZG0XYoiNKfA0uYjWTXLwSj8RQdQoxSUfdoFIbgquUhkWrprCug1TmoVaNJarez3gwKOZn0UamsjoxAh7Dj6XuS0mXXk+ckyRJktUlxXVIxHC5eCNbVzZwLaTiorJ1I7lJXaN4KFEza1OclrgSyUg3j1o7ruJoQCErmGtbMXg9LkwDArV+CuS9RoyB8nwsVD+PJuyKyLmauZAJrho1SU7mZSZJkiSrR4rrkCg+JmJRM6gJe3QD4aZlPWrmoI+oOkPWp7pT7erMWpT52w0dQ2Lyg3ixpClzGSUtyToWX/UaLFAWMKEPceV2Jrgy5iQ9KaK2AfCa6mJ1O1GcLatYh5No+TUPSNjycN4nOZ0lSZYVoa2oNGijX4MFa49Ne4aZupPiOiTctxKGwl1bt/Uifi66mEChyw0XruxlYqh7yzBwPWtkrkMRgZQNJyFJkbRErT/6oz8qDSmi5ZzSH63sogMQcfXaGlGANewY/Z04bbiVZxHn1XvRt1fCGCudsBrVB67zUbpPSSKTxe156lmZXq/beLJJE8l2Gg0MO+TdpqluP+czV27V7bgvvfTSDeaZun5dC22o3W7zbAhjKAFrm2PqWuOViTnDTbRf7NWJbBh4ckyHGnY4+zSQ0W+DXfdg5tVqDkMI/G49SADWkl49qHm11L0Pe936/Os+yU142HSFaz6vsj4beOuHGn/5Im0bdddCr8/ItVTnocC9LheF142BMu+kuA6JGyMSlRB9KWUCqzuth/XGyDm7RAvasLA2WbpitZq+W/RiIICuTbrGuCDrfq5arBHhmIJiEWf5RtcSi7lpO4SLuPQbij0NxIstSDpe1bjZLeLwL7f3sBOAnDd/q3NViKvWhc6lc70WPZnF4DWht/kaRlzF5tv67goTaNjexPuySNVt8OC9t4mrDYznb573QH4Az02zXaCFtq39ZOB8uy6brfyGxf2k16wFf9bFVVKiz1Y7vhBXQwd6bbB1IGqKq/s++jh3Q/WCzfuguG96CSs0xyek9Qa8+bXryjXp2pMwWWPzb53phuH0DIN67KKm+64VD9dgtwlF80KK6xDYVbEmoxWanpzqSqHUpTkzk2vFItDcoQVcxxYrGb+9dp5KfgioeKrF304VdrTcvnZ6Nb4f4qokyM6y7nWqwYW/M+ZLotMsQVgJQizw+rfGlBtWWz1ByHvQLGQYCIHPKtzpej6vRQ1wHDuXfFwzw+L9Bq4ZYqMEq264XyMTvSmsaGtVWJ93G8U6E96iGi5Er9WrF6/NToQ2hEIiZOLY+4lEP/QvngdssnkXeJvqyUhNZO/zwARKCHvh/g/x1d85qgrUs2u+3zYsoh8sX+GnuB8CfYtr4XOdWf8C11B8HjxBpoJ1W+f0NY4B9Oecc07ZZPhbPQLqBjdyQpQbel+ul+ZUoXkjxXUINIKwMLsJWB4EKxpSs6rqSR3Qv1JCUxPxQxcV4fWcsQv3u2GJWaDC7akFoufmutQ8W2yWpcCNRDwteGpeAy4d1moILOvWDRQzDe3+lQtxG7OGJz1qaVQkftk8OCdw03rfMZjc9x27jGp0m2TSDTtlNzZ3bDTjJ3Zxg/MwyNgepCerc2p33w2ffd2JS8x8mIEBbcfOZevak2XOrcbt6DqwSbMgsbxrV3mEJyS11a/dtCC9F9eP88v9K/muvpZZtETAea+T65p4vzqVxZgztd82dsaJxbE0cd84Np+DxdzGsdtknbie682Qa8Z96DN1Pfj83A+uE9cNUXDenC/vwca47Xp3bznOCPe4r5wPghEiI0TjGoH32JwYFLiGJRXaGEYYA3WjGTkbBLJXUxlCFC5kmynPG9eUenaTkWyQHXvcM8OiNeog4SEeLjFYHjhC6licY8dgLCRruFvvaqP84jP1e7H5al4TPpfwpAln+GzbBtfPCymuA6Ku1UWigQO4MHpl3Vpcm6ORXCwsJ4uXm0F7Ru4Ti6Q4koxfuDHdlHZx9SQNv+vitqMzEYeFqn+xmGotrnaddrmmSBAAGwFuYAumBcgCIhHLzSAmy0U4auP1SaLpRowfU0bEhVY3QLfwy9QOy6m5memHcVUW25iyI/GrdsMZvM5dpcVkL4uDG44Ho80qDJo9nb03CwVvhmtpWMTyHbsFjlDA9WJ4hIktXJBqmiPhy7Xn9yGswLpx3TiG5qbE70UnM5nvFvIaJWdx3mMCVBsWxjrhzGcoO73NAmG964Xt2q9HoxFwm0Bx4rb+2/UYMpisY2PBMiKEsVHy/llCBDFmiPLSOE/OX3OijPdnwxmTbjyPjRjXfQz3tlmIqTwSFYl9M+7vdd2bCA9TUE/Lci33SwayRoSYuw9qoXEPW2OI6zjYeDjepuUa12rgmuGu1bBGDN29FDF2v9dtQg/qe6nXfYVozm+DZNM0bihhmqS4DghhdCHX8dZeuPHiQnJDuukshNwhFpC6c1SIariIxFWJITedEppa+OwyiaVGEtyMLngZxRbY2l1nsSHeWh+yDs4666yyyHBFwcLn+SVYcLvWLp9ZgGXQbeTZqG3OYrGLYcqsgOaiYPfczz3nd4bdUTtm8Xg7+PB8DIPPdxjEu5R2gWVLPDwsoqzLbotcc9B0MMh5t2lwTcV16Oturj0bmMictwlxbnhXbFhCyNtGxrEWa8tWshsIBItIcpd7zfXuwbvD2xOxemJsU9kcsuF53N8hVl6fuFrgI6QidmoTzFslxum4a6FHfd574V6UvV+LGsGuXbE1rFyfQcz8de/7HOF66tbQph+8Fm39eG3M2+LDrg+bBOePdQnx2zA62hD6sl7x2EUv9m50u/7mkRTXEXHjdsMNEsLgZuRGsZi6YS3w/bKG7ZTdMCxTfyO2VluwFjCuNFaBRdfvu1mbsTDuQ8JKYGGBIc7hihLLdZMSfS7pfrvKaWKhY6l6P4H3M057S4ujm12pFFj7Fl9u+F5YELlKey2iTXef5x6HGI4+LhZECSjdsoWbEMDaQ0O4ei2kLH+PJs5rjWuVBel4fAaSV7hAwxvg/dbiSniJXO2haeJ+cH9x6YaFyWIPD02/hT2QRGRzy3PkX7DmxfeFcNxXYAXX4iouHZsJm9d+5W7NecMS7LqJK+JYaljAzk2dkTwuBDzyHNoQl6+9L82cjybuUZsin0HkpXifbQ1teOasS96r89trMPqsk+I6IFxYdpp2j3anYW22YfGyi3YxuRndZHbPzVjSRRddtBJ3sBjXma8WMK4xZTNckHaptQWrFSLr2DFxH1l4XMTN8XJifSxlCTWsbsfNMuBCs8C5wC0QdqLdSilmATdcM/vQe7cIDDJSz1Qi7lGuuFr46rgZS7afsAbCAt3iiLAZmuagejF3YiXuGJm8LCPXic/cuau7f3VD6UsdWya0vcS1xvvnZmWNNK0jm0fCzeIkhDaS4U5tw2fHlew9dKNtPjLR5q4mut73IMlkLHTXQh0z53L3dZ3B2syqZtGGK95775XL0Lzf0S2GG/BGiSnX8VUixCpswwbQGgR5BHIxmlgHbFJrC9px9Jpfy70eGcLi1LEJ6Xb8PrsYYALHIbktOsjV+KzivI8SPpklUlwHxEXtZuBGFJ/i4mgjWg1GTMnO2U66zqRzodmVEb2wxCSK1K4dN9Lznve8kizgQrQYKpN4+ctfvnLTsoDFKFmeFnsZipr1125NNwlXsEXSjlSs1SMWKdaBRUEdosXHojyt8hyxG7Ed54dVyNoPgXLzsjBtKKT/g6UwaCIHi0jih5hOxNBGhWvfhqfXxCWx3ElmO/q8bBAGRexTTLlGNqlEGNcct1/EnnvhmuECd677uTtlvIvJCVPA33WzNOUVuAciHMFiEXrpxjClJm1wD8/S0Apu3gjRDIKNsBAOdzovCFGDz9g93AxTWFtszGMzIf4se7t5b3PHD1ODTPBsMPyddcm9xAK3se9Wm+oaqL11ygIdz6KT4joC3WoTCW9MoBG7sTMnhrWwij+wSLlxXfyROSfeWtcq+j+XsucjKiwhC7qFUeJNwNVF+E877bQSn+XmbWb/EXkWC3eX52RFq3U0/xXc1naRFl4WbC+X0GriXFicCajEL+n44U50vHHMFspR6efCGoToTNNNXHkYWNqTpF/JlEUuEmRsTuK88VwM09Xq8MMPL5u6OMfhzSAEkWzWDeeFi3IQhDNCWB07N7DwRbhcm0i8YV0NW9c8aVjhsq+bZXfDMmwJnOQlny+R8lmwVnmznG/u5KYnjceiLt3COJsLxoQ1yudG4Fne9XuwJnYTV5v/fnkMi0iK6wSRtRtF/oSVmySEWB2hn9mxe3BTWQAjI89izLKy02T1EFc3DitTzNWFbPceO1huXhasi5wl5waTzeh17VBrWIOsFMJFfFle3NViUXayxN9u2N87rmFrRyeJBdfGxHtQgO+mDnc8NyeX9rDY5UeyWK8azUGRbMVF3c3F6DMdp4RAiZSGDTJWI3uSy9MmSWYtK5aXQ9ayz9514BqJBYwnwkZLXgBPhix310vUQTr+ukTMpkZSivCAjZ/F03XrepG8YjO3mrEvbn3Hx8vTC8c97bwAn4f7pU1chRQkVKl/Vz8tozbKkppIoOr2s364Z60XEh9ZkjZDPF2R6QzrQd2BrBuuD8fczBZmIEQuAniIvC/Y5LsnoyQOk0pEsjHsFR6YJ1JcB0DMySKvDMLFKFbaxMUYN4uFyu+zJlk33C4xpo715aJkidap7nV8h+VmIZTwwX3HzWanSozFTVm84miEyN9ZyAkytzDLlIVR19dBjNYiylXpZnIzeP6IrbiR7HRZ1Fw8Xnca2JCwYiSQWIC4Qr0f7uFoSBAoQwrruxfExoamDVaIxdLnRUSUbohB9Yu9jiOeBIIwtgkF1yur3bViExXi6v2z2vydTVdtIfpca8vANWEzxcXverDIWrQihqW8pI4HW6zFFIm6xDECHl87L83zPmmcd/cED0wbQgI+v2kLaz9YhvE5sPhtELsJqM1zLV7Dwtsk9s0tzGVvjfC59aqbbcMGkbeiievDNRMWsQQk65iNN0PBI2CxTqqzmTh2JO/16sM+D6S4DoCLVnIA4SFodXA+sHMkCISYyBEwi55G/kTW7pywETOLWz/8rTgpUeTaY7HJrLRj5WYRx+CGZi2zTGXSEgTJU16nKa4gUn7PYqleUSMFmwVC77m4mRwn17WFfdg60kkh09rri+k4j6yAQAyQePgcJEb0SwKpsWloNoiwybAwOQ82QF6T2zzGCa4GSqSEC5qt7sAKtYjZlDVbyrkeiIwEIELkc+eCri2IgKWrzMJGT8wf3La8FfUUp/p1WbuuGwscS1ITA9hIcDO6vtsS+Xwezusw7epsGgiEe8vxWbzrz6ZuF2rDIVQRrUZrWOCETLaszFmwqlh1xKcWN88vjt/WfETIxP3heoqcBkJFMH1db37lR8hxaGsQI/7pnmxLxuEZiK5GzRKeNiRAup9ZcjaBTaIxTLjuo6FNPwhnv0YpXNB1boJNA6+WHJAa5104qT4/iFCY67A2IoahV8OSSTNOI45upLgOAEsiaMYxAqUNMvMIloWBKOpjSwS4+FgRg2Rn1lgs7G4tENy4drvKHKL0hihYbCVHgMuTtcHqjZ/XiKOJORJWbj7H53iJqiQDcR2vx3KTMTktcYU4IeuLtVI3GXC8jnMYLJg+B67vtgxeixQLgJh4vdUUVlgQo1tWG46zrXQnEtLARey6cJ11QwYu0QjxJcS9Sja891j8XRNx3n0WvUqeWC6EfBiINfdzZNQ7zm7ibFFvNmQIxB+biUHuj7bjqZs4NLHJsrnQtCDE1+YnNhY2AkGUG7W5Xd1HYb1aN+pEHvfeMDF/gmrT1w2by+hfPgxcwMN+XnBuBv07WeW8Xz6LYRIkY621MVorcbXe6cM9TMLgIKS4DoAbyWLGTdnmXhSD8LBA2/X7ffEjrlsLtR13s9sM67HZE9aH23Q5i3t5Dhl5LGIuHP/3Pbt9x1O7cVlddrrRmL+5o4ySB7E1FmpMh/F/N4/vs4C5oCU3OcZptiBzDM2C/16wPupaWOfG4thm9dSIhzeb4nN9iUMHrL46rjVN+r2fwAI16O/WDHveRyWSAGeBthKjbvXJveKZ1goWW903d9mwIRvlc40aaV6BUYadjALvgI2XpM7a3T0uMyuu3C7iPtEFRIszu8dw/awVMUKOe4g12FYuwH3jQyFoMaxcWYuFg/XVFFZlIawl9WH9iPgadwxrh+XseVmrdrZcMmKPLGM7MLtuLkfxYcLIem3GYfxcghShtUj4PW404up9smy5Du3kva9169aNdxLXEOegbmIgu3HUZBzWm+Qq7lkP55twz0ov5mQ2EbKxVvAy2HC3TTJK2lGiw9rt5dmZNFzkvCfWw4UXV5l4FjPJO6wOMTexDItkNFxfK4hO7ZZsQ4yMlcplIjOTBSoOwh0s+ahG5qqd0rA9Qbn2PMR2Y0JJ3cxCTJY7SryVRUsgvTbhbLoOxXO5fCUhaCbOinbM0SRf0hUL0E7O5yDGOy8Ca3PD4go3otjhqPBG2NiEJey6HDSulSwvwhBi3TxEo7YlXFbkqCwKMyeuYjAyYyNVXczBjsJOUDnFWosrxAw8upVecMVKWnJDsZRkuUkSkrgSsGZZg35nnGbbzTT1cCPbHRPEaPPmmCTnsGwlCNUTK7h5xWVZrWJEXDBiXjwDrD6WLhG3AxcD4Vq1C4/M1VnFeeUpkOFqAzNO+Yh+vIRaYoaNhYS2JBkUHrYU1uVm5sRV1lY045aiLwmjX/H6akNUJAu1dTLhxhAMlwHMNWtRlykoYzAYZIrKuMio9Brc0eKxjsUmReq8LM+YrhFI4BAbkols4yJ7URG/zQx3PCvYeZdEw3PgeWddXCUrcZmzLgdpnt4Lm6GoF25rG5ckSdKLmRNXVmrATRnxLe45LbdmDaLEohYL1UVGjRa3ZBRVi8NKROrVh3YSaA4Rg8Sdw5jnyrLlPnYcza5BmhE4dr8vvkhcWdYyGmP6hvdlfiYrsK3R9iwh9s3C5o6H62eQsqc2lCJwtcfkEc/Fa5Lx1iRJBmHmxLWuNarjZWJ/Ske6ddhhmTUtw+jKMw6yZ8UwuxXSa0guycmCzh0pZilhiAVupidRG0ZYlcuIL7OAvbaMw2FbrbE0CbpWcuKnRN9xEP26fZxEK40klByIbxNRAmvDwKUMoiIuK4YsRismMq3ew4MgKWucoeSB9yie3WtAQ5IkSTdmTlxrxAO19hK7JJ7KUlhQba22xAbrGCcmURSsYw2Rrt28Nc30fcKqEQNhlcXbj4hrKrRWv+n/YW3pPiRL2DEQShnUMeWiF36HNcpNylolNpoOEFwtFOsZppKeZAh7fyxdbuEYGK5+UbxW7FFavfNLbMKqTZIkSdqZOXFlXUUxLxelpADJNhZ0Aksk2sTV73jUaITQnJm4mhAzAiYGO+ikCdm8BFoiTtvfEGgPqencsqxZMdxB0N1IHDYQfxXDbm5C/A7rlOXv+RXli9NyiXLFi8uycsViY/xd2yDzJEmS5JfMnLjWYiBDk7jqnNNrHFWv5xpHXCX8sB7bOvYoktaGjshoqYbo0ck67NYnFURUBip3rCYONhPNZg9taOvGeueyZUEOYsWqVa1hWYtN1lnX6je5grmOdYGKYcVqZJWhyJiNz0UzeHHNdJcmSZJ0Z+bElXs0FnctBS323KEycMXT6jZkqw1BdzxtvTFZ0cpfojxHIXLMSO013UNzB4kyRFUdqTZhw8CC9Do6QSn5UTIyDI5XklOzpIl7WPKSUh/dZZx/71+s1XESWLWzMrjFZVm2bf1OkyRJkhkUV/E/dZdiq2KNLCXoPCTuN+zUh0lAYDSTqHE8cWyQyMR17bi7NS4gwFyqSl8kGQ06+7INyUcsV80ShrXqWeQs1bqXqzis55S0pB6XO1gylbFvMY9R/Jtr2fuWjdxs35gkSZL8kpkTV0joIUKaIYgBshBZs+o2p4Es4JgsAhm44p91E3RWH7EjXG1TcwgrF60uTjKfdVIa1woXp9UQQqOIYdDSkeWq6Xed3MRVLetZ839NKIgrAdWcgfWqMYYELGLrZ0p/Bhn5liRJsmzMpLiCwBIqCz0BqEVgLeA+1bSdgDbHLDmWugel8hkPlnXd17bGdIxIGJKoxcU6CSRxceM+5CEPKRnKg+I4WeN1A3KxZT2LWajcxL4W9yagXN3eg39NTjEnlHWrWcMsl+YkSZJMg5kVV9TDh8fhta997dCNoImGshQzNFlrNSYoyMQNJAhJYFKH2wYrUbtBFmsMT/feJkHMm9TTWMmMEhqW9iCI+xLLevqJxCXPxTrlvrbJUadrSg5xJaTGtzmf+iRL4hpkAEGSJIuJnBhJjowG/c+NtEtmXFwnBREYlma7wF6oByUy3ZpFEEBWrUQi9aerMcJNwpF4KAFvG57dRJmSblKsXtnNkQ2s6biaWha7hhHi3zYnjt1YO32GubNtGCRmqY2VOZwtApNkOVHB8LnPfa7832ZdImqyJOI6CjHijpV6+eWX9/zdZlvBJpKcDCH4/Oc/XwZSryYve9nLigj2m96iU5NewcTTgHTNK6LRuKk5xJZbXmayG4ZlLoPYhB3eBK+jzEkMmTh3G2adJMliY+PNgMiJUeuT4toDg7HVeXJ7jAuLcrWFFZKOZCE3R901UcajOT3BdHOI2UpSitFyhNXQdBsH7RjFvk3+MfVH7+GYF8tlTly9P0lbSZIsF1rDanQzTM7HMpDiuopw/xItIr2WcUkxXRnLYrC9psPIcObO4daR4MTVK+FKVjY3s8Qmv6M1oq5TYrFE1LQYlq9aVztWHaOU73AxE921RP2zrOcmjo8FvtpceumlJcFLo3+f9Sgo9dKQROLYb/7mb7b+Ds+BAQyBjHV1320olZLdvvnmm5drr4mpU5qfeI42hDduuOGG0lN7mrgmu7UwFdfTbWw10Gfb8/d7/2rCebV4eVYj1DOL8FbpQgehMF6vpJ2lENdpxAPVwbrhJAVpFDHMNBXxXt2Y1KKK5w4LwVOHSlw8T7d2iQRRGY9OURayH/zgByWLmbiyRpXjeH0LCEuXuBIzVq3kBaiNfdvb3lYGABhWQIzXCglnbnBZ3U2ipni1BVYymNCB5h7c8bpaDQNXmnOpfzXPQZ29HfCcGOSgU1lg4ZdUJh5e41h4FvzNXe5yl9KEpX5O9dWxebr44otbj4m3wvNM0xLhIdGGU7OUNrx/XhPvv67XHhdeH5tSwh1Tppo4JmEQ4R6eLbOSxRlHuVfdM7xHEoLkOnQbTDIrCJUJcaEeApJsyFKI67DxQBe8loYEUZLQKLjZlKt8//vfb7351Y4SpTYsoqxDpTKsw4AIskYGXUy4aoifxTJaNNZYGGRDs1BZXaxY3aiIkmxhiUoWDMJKpMVauZItKvoM6/FsAyCBStKYBhSyqNdiLBshYik7vzYx+jrDZ8fqYumxxC3SsRhMEq9jISZC8JoywYeBd8H11Wt6E/H18xBW55Y3gitOdjqvg2z1wMIfYQz/WrBdR9FljFVqylK3jHIlZuqxvb9p4thrYZVoh/h8vX/3j+vTZmJcnGfzi13nmrLE59qGXtt1ZYBNiM/B5mpY74XrVyUBvN9ZF1ebmjaLflks92FYCnE97rjjhirFIYof+9jHipVm9z8spvl4sOZk5DYvPPFL5SxGwwVuWNYENttss+JqYvHWvZH9n/tRFu8uu+wykJXkeYkxIWpD4pbF6jnPeU4RVxYSV6K/u/baa0tWsdcRX7W7tpD5vu9ZhDWXMJZOww+Lvk0FkV1NuIHf+ta3loXJOeMdiOlEFmXnjsuOy1YyluSrScKSN+jAZzgqjs057GY9BrwYMZGJy50Ye78+N3XTvA8aknSDC9hnp4xqELw3G6Vu7ulpQLCUmNkg2BQ4794/bJzHFVf3oZaeMQe4Fza9MeOX18K9IpRiw8LSHma8pM92WE/HrOKel6+xzz77TPtQZoalEFeL0SgQ2VEGBhByzRi4i3SXgpaIGu5rnO//dsouRq5XWbpEotkoQyJRDAMg9qxGrlvPoy3hzjvvXKzKZp/gJpKbvJ6GE20WLAvAc3PpElBfc3OyXjWR4OK2SVB6Y5yerGeLCIGxAeAm5nrmWvY972sS1kQbeilzozkesFzqsX82Q8TXZgH9zg2UF3Vr/gHnuh5UIO5cNxEZBZ9tP2FFHasXI3X+PbhDfabOQy9xjecYVFzj9dQ1B8RWHJ8HQOMQr+17NlWuqbhmwG1oY+banxSeMyxv9wkRDHFtw+ffayoVD5D7JnAOBxFW2KwQUsmJ7kP3ho2ckIl7S/x90Fiwc0es+yHWLucBBDneu7K+aAfLgLDO2YCZeqWGvYnrjSvdJsDxh8XMEnVO4HhY5TbxYquu00Ea+JhrbbOX/cZ/xVKI67AQC3Wp3J+so2HRBlFSiRpQcL1afIh14AInwL16Jcv8jSEAXLcWedYld6/F3qLGjeVY3QTdsnU1fmC5KpthTbcdr2Mk4N67xVFpjsXTMUgq4Xa1AHktNyCR4xYlyBZdk324hFlJLAsCG668SWJhC2HllmYxN2F19Rqe0MT761XX7JzX4ur5xZtY9V7feR0Wz2GXTxhZoyzxbr83Lo7PgsxF3A/eGp6OOjHNwv7Zz362/D+uafjMXSc+E5szOO/OJeGZVCyUVUmsXYNeqxZC90UTG75enyfxrcXVZlECk97gNr4SzLrh/gDBIaxQrkZceYC870HElateaKMfrk0iLFYOXjBZ/KxtseEm3rd8CxtOk7tqCLBNsIe8DCEmiW8xKxvK89zb8T0eMl64ftj8pLCuT4prC+J1buZhGknUcI3K/GS9ERtWVJ216ya2QNgd1g0u3DBhqe60004lucjvuKG4nww9tztlhbgBJPLYLRJDLmM3uR1ot65WLGoCKjO1CYGNTlQWGxmTLGrPTQDsyr0vi69jU5YDizZhdgNGZxZiJBmk7vy0Gmy00UblETjHjqdeHLkNHW8vbAp6taNsJqqw4MX+uO+d6351zm2YLgTJdt0SZ8C6sDGzcNuchUU2TE2hz45r3EZsEO5zn/t0Tc4RE3SuuAFZbEIErFkCYJNgw2cRd6y1R2EcXONRItakbUPpmu3lbm0mjfGEcDfzDHgPITRt9BolOQxcybxQ7lnJg91w/9tEElfXGmvSfckj5l6E9cTzif3yHPEq2WDUXeRqbAycIzXu7tF4T6xdCXDuZ33LYTPh60VDfLvZA949NklSXFcJbjWLvYu+FlYuLguQXbgdedvuEy5y7h1uTTthLmCWpEXDLpmlwz0p/iPOSJTF5uxKLfZ2oE0sHqw+z1Fb0U3cnBZ0NzGxkkTDBQV/772Fu5vQOM6tt966HAO3mPgYS89GwHGvFV6v6d5jtfXLem3L0O3FKHH4JoNmsLNcXS/EzubLdTEoXHVi4oZMwHP0yp62qYoFuxuuLdcPrwVxhbiv3tqykInBWuJ6jGsxCNf5oDQ3aauN65EnwCQt2fq9xFWSnHUCYs/yLcADFa5cHi0lMTZcxLUfXMLhKZEsZ10BLxUBZ60uOjatPIerSYprAzcrq22c+i1JQXb/doWeC+oKuYzs5o3SsxD16/wEu1vWLbeuXasdpQWTBUpYtSl0o9mlctn6ncj8bRNYi6ASFmLYC5mThEqMmNUjButmdvP6GXGOLNXo8MQNZfHl8iL4jsMislo3q4xRVg33FrgyiRZralD8va5TGml0QwKanf60IP7hsRgmYcamjNuaq9NnJnZX18o2sej3271PI5vVAAnWcGSEey/el/inzav3WXseuEXlC3SDS3iaLfpsXLl73Vt1TofPyaalTr6Me4p1nUwOn0G4+ANGg43KpEhxbcA96qH0QWr9KEgKkSATMRWWDneT+Co3pefl1o12gz7kZiN/lqK/t3O1EEh8sstkJbgpuX08n10v4VXawzUXFibrws7MwixGU0NgXUiep5t7MXbBXteunms73IssHJsDi4DFQAyWuCr7kalL/KMBgMVPnC4WxnHhInf8YkXc29zu4cJiJZtgZDPClTYI3hvLvJeoDJJ0stqIadkwRXIJV/cgrmG/Ly7OrdjLpWmR91lhmNI1bs3VriOXn1Bblq47blziyj1vglWN66PX5zlOMppz06wtHgZJRSH8wi1hlYKXxSbBdc1j5DOX89GcJZ2Mj3u+WTI4iSExNSmuDSRMoFsN6iAQs7p2kbVKPLnl1JZKPiIIvTIq7c7F4uxYub1YwRZJu3S7eIuahUVmH7ehuBdrlkuWcHLvWZS4jsVMWJ4BobMBcCySUrpBpDQ44PZ1o/uXxcCVxcJnAXh9Ii9ZhjUcdbEWPgs28eduCnfWuIgvseJYxY7P+5BBGu0e7fS7TSdqQ9KVz6pXfL1bvG9QbARssEa9eb0fdcUSqJpJSVG+1QvnX3zN33YTZNdS1McOI5Y+j0E3TkSQt2HYLl6s9TppzHuoE6uauE65xLsx6MarjTg3Npridq6fOBb3WNPj5dgJpOvSeRIi8pnZHLg/mtUI3pvnjc/JpsK1HglNyfyQ4tqAW9UNJFGCQAwLkXNz112DuGE93IisVBbeIAuSpCguMf9y+0o44vLiBpahS+gItd2uDEguYtaqjYEHIRYHZdkS3iYaQHBV95oaxEKWRMMaAGETNybKknJsGuzEWbjeG3G1EeCSjkQdcdhJwh3tHHDV2kR4f7H4cK0NI64YJj43LFz33M6uiVG7V8nW5U0RO434aRCein6wuJyzfqVlrP/VamHJEyJ0ITEv4nyDIHmqW+20TUvz87OJEZpZDWR421CoU/a5akEZ857d03XXIiEd9wrPhw2vjaB70r0a4SJZ1rWnwL3clgGfzB8pri1IIrHbH1ZcueDccM0Fzw0nU1PsZNjB4lwX/o6lK1ZLuMRCJS9xHVmw3cDcwrL9LGB2xRKlvKafcdVKjCKktfVkYeB65kLu5jK88MILS/IDa1UihPNC5C0AdtjKbpRDsFBZVkRE3ILFHTFfYmfRtrBOChsDXgZWQ0zsaeK8t3XYsujZNDhHk5qrqwyh7pQUyKq2gMZiOgoWZi7bpqvTeW7GQC38Mrd9bk10q9Lxq607U7gebd6GsVxdP6yzXiVlECaIshnnYhhx7YYNplCIa3Kt4I53L8nO56aPUWvOezPj3OcVIQXvP2qI3QuR6Cc8FOLqfhk2ycZaJb+jRolQW75FGzL8Zb27lyK72+fPCyXrflyvzTKT4jpBWBfRvKCGC7etHm8YiLIL3iLIWtP4gFXE1WfRdGNHbSdB4YITn3QTszYJLAuPSNc7fTcmq9qi201guU1vdatbrTTsJuzcxETXQslaJHYSi7igWa9c3qxJJUThxuOinlR8jiiK/1romkMRbEhYOjwFMjJrLCJcrFzpFhWu83EIq9m/bRawjZHj6NXUwKbE+W/WJQbeqxwAXohI1uIlaLMwfQauCxuHpqXMA6JVpY1Is8kAgfKcNlFNxNBdZ8Qsmjk4FtekjVYIK7eoGKKs5mb5k4WbwESeQT9sUl1TEs7a8DxCAZOO97qeeER61bfzCvnMIvbKBe28RWJdQHBtPiX1xb3ThBDyArkeiWzbZs9mSVlf3dgjrhnXerxuHDs3sk11E7Fq60C9wXbsYtA2gNEmVFVBrDM5+Hx0UlxbEJ/SBGISqJmbVLwRUQaiwYVkHoLlxnVzuiFYs+KukqYkHhFarmoLrhuOuPpePf7OQuhm7ZVByVL1t3bKFgRWk/iZ2DBkofo5gfAzx8YytqlgdSkR4sL2/UkWmzt2731QxKvj96OudxzExHqVUoiv9fv8BykFseANatUQ3W7nROjAo0lkpbbh824m8bSdd2LbLas6BlmgueFpw4akVz7AauF16ySjNmw0bR77XXc2Irw1vTw2xNQmwqMbytrqJiZou2b6HbtckGZyI9o2dZMoN1t2Ulxb4E4cVVzFXaLFoMXEgjWpTNkaLcsik5clxjpmmbAyxXRY0RJUIrnIDpQFywVsZ6sMKKwQsP5YR22xWbD4CGwIsMVSaQ6xjOQLsVXWjwxlMWeiHhnOXJHE34I56V6/w9CvVWCyevB4SPhZy/GLSTItUlxbkKATBfLDIOYqBha9jAnZoLGPUfEaRM5ummUjZibGGVmLYj7iUmJENg2El2uIS0kziogB+5flyertNuZLLFnxdWQec4PaeYe4Ek/xN8kkjimSjGQ7S2KB8h8/m9YUDQu84/GYVLw1GYxRS9uSZB5ZSHG1qEv+iRZ9g0KcxHhG7dzBWgxh5Q5uZnauBlys4otiJ7olyQaVjSyGwkpktUreIZ6+FlfhIibKXMr+JnoAy4SU9OTYu5WmsFzrMiOvG1a+OK+4DwtWPIyFwk0t/kfUowGC55dpvNbdfGrU6aa4JkmyWiykuHKVSlbpNemkDdl9BHISry/WyJpcK1iqEom4iiGeSEDFGH2PiGqkLnYmfmdcnBgoK5brOqamsLzFEIlj1PzWSJpimUZiiriTciE1sxIrbE6IuOd0TNzHMoi9vrgu1zWLmei3JV0kSZIsAmOLq6Lobt1QuA/XYnB2E/FFDxmOsmrXGkIyjf6ckmckNMi0ZLlzgcpSZd0SW4lF4qy+L+lFXNRxciXL+IxEF4Irq7Qt8UUmKNeuDEixZNma/l5mKhGVROVvHYOsSslhMpm9vqxkVjTEiVn5vYr9VwPHvBox8CRJkpqRxVX8RAYoF2y3rDkuQou3NP9J1LWtJuKGrLlxkUXYJkprBauZpep8cwUrDWLR6qikRlbCEgsyGrj7HJXUEN76uFmYEpLaxmKJrYrPRjYnN684LytZZizRdE0QYUJrk8MaJraK702j0LVIec4gjcYnCde3Dcc4XXqSJEn6MbS4yjLlFtTovB68LUFEBiu4BhVXc/95sBRkrnabADMLEFfJPGKKJo9ccsklQz+H98mim1ayTqCGUQKRDGJuWZYjoSQsYp9cv96rpgdqZ3V/8nPWJZEMjwPXrmbu9VSfgEgTcXWyynrEbzW4J6iE3NcK5D0HF7MmF6xUoqwm1HMSZzHiXq3sVgOvG7M4kyRJVoOhxZWwaizN8lEkzVLjeuWGjQQVBdjckrJuxda011Mg7XdWe8bnuHQr9h4EVtu0hRUSdViusoNl+CqFiUkhNj1qEVmzNgJ+R00bq12Jjq5OMoJ5HHzW4e5tonGE52DZEmjlNTZbit0lNBFwlioRczwEnEtYbNfPWcyyq2Ux+5k48FqRwpokyWoztLjqaGOhtnh36yijULlu8aXZgPheW3u4RYEFx906S+hjKv4r1mlTw2olbhKbJDNJeGLhOna9lAksq9fvatjPkpWUxLKsB5AHPlcJUrKibSp07THFRwcgGcym4sTwdxnKLFgWL0ta8wnxW1m7Yrys3bqxRZIkyTwztLhq/j0s3MXhMl5UlKespfU1KBKVCKksX9m53MHEU7s2iU3aE4qR+h5xY1VqAiHhiLhq2O//3Ro/KKlhebJexXi5ilmtno/FXPecFZPViIIXQ7MJx8N1rL2b2lebgCRJkkVg7GxhSU0yRJuwYCygrKVoCD3LxGSLRYQblFUqm1jSEitRi0INJpQr8UQQ3WiAThSJI7cw9y3x1FQjGkE0YQ2LrdtA6UPLEuVa5q0QgzVoIFD7KslKjD5myvKGsGQdC2FPkiSZd8YSV4N/xd24B9sQUyO+8yCu3YRjECQKecwyPgtlOuKtYuRnnnlmETRCx2XrcxSPFYNVphOj5Yghq5zl2u0cxUQeDSjUukpcYy1zDUtgYrHGCD51xI5BPJZ7mEs5Wi6K7fr/ons5kiRZfMYSV/E8wqpZgqSVqHeV6KTDjzhccwzTIqJhRD2MfFYR8yRuXLBETVtEJTKEVHmKbF9TbdTCRicnDcN1fJKsxcUbXZaaEGstFXVrstHwXP6WUBJN2cORdcyVzNVsnJXXlqks2U2JjuPhsp5kc/8kSZK1ZiIdmrh/jTEipNx6ElpYR7r2/PznPx96huk84b3NU6KWMhifFaHV9lDCksSmo48+uoic92KKh82SOKpkJhasjG9CqDOT1optaPzveTSQYAnrq6x+lrvXFBWjrQKv7/m4olnFrhnizE1s3iq3dZIkybwyEXFlqUTXGwupbGEWC7exhbM5rmrWkNVqZNooxBDxeYKgyhhmXYqPskhZkYRTrFTj/hj4vu222xYXr9pQ1qvPuZu4soo1pBDX5b0gnp5bvNdcS40pArXQYruSqriObdAcE2uXO5nADzKaLEmSZBaZiLiKoVkcZcuqb5Uc063x+yyiZvPkk08e6W/NLJ1HdM9Sw8pSNd+Vx0FSkuQkmyHlOdFvWO0vUWWNyu7thbpXYsy9S1iJpPiqGludmpTmiOnqWyyDmeCydJX+EFYC7rW5rImvJKwkSZJ5YyxxZbXJJmWtcgFbEC2gMfhXzNX3FplZq20dBgPXZerK2uWeNQhdhyauYwLLI6HBhG5NOlddccUVRRDh+1z/LNUmLFYbLq0PWaUyjyU0KePyHCzfyCiWCCVuT7hlEGsq4V+CLMFq1ttmJkky3zAYdORTdz9JxhJXlqqkF9YGC07s7oILLihZpWJ2FmmJMYsKcZGFO6+YHCQ7l+XooWMTgT3yyCPLeyOKxx9/fPmeOC0rlHUrJkpwDR43nk8iUhPPRRx1feJituFSxyr5y/dYp2pexV4JefQ3job/EHcVh81G+0mSrBYXXnhh8dy1tXkdh7HdwhoAWHADLe5YrxbjWWyqMCm0etQwYd6TtXTZEhNlSSq7EQPlilULy5rUG5g1Cw0nCKZN1JVXXlnEMcptmnD7aoUoRCBT2PPKUCbG/k+YPW/MfLU503pRGU/UTRsKwTNiMECSJMlqoNUrg4ERME772yYjiat4qgVPfSPURh500EEljgeCu+hI2qoTdOYZZS9GwxE2SU0+R5apGlglMzKGNZoAgWXR2kTJ7DWQ4cQTTyw1rk005fe73M8ElCgTUXFe2ceEV4MJ3g/Cy0rlBg7BBa+ITONocJEkSTIPDC2ukn8IK3dhQGzF0gzNFotbBiTlLBLKqHy2RsDpM0wEtT/0PSJqalDEz7lwWaMSkMQpuHq5gWVdNxHPYKmqbVXqw2IV39CYQkKVVomsZLtHWcwSn8RrWdMs12uvvbZY1THFJ0mSZB4YWlwtqhZSaDyggQTLRlJKTDiZN2S2DoOJQDJsFwkxct4HyUYEz2fKgiWoOjmxMH3emmVwiRM81izLlBtXti+Bbou/EkpxDQlMMpC5k/0rtsv6J8pc7BKeJDj5fYLud1xffi7pyu9rcJEkSTLrDL1S6UeLiDlyH3L7cfNZEOdRXHUVGgYisqgt+tQl+0wlGhkdCG5bmyoTbFiQ4ukQn+C+ZW1yISvD0eGpjac85Skli1h8XlMK4qzDlxphmchKuWSXs4LFer0OsTVIgMva30hw6jZAIEmSZJYY2QzQVGCPPfYo/7dIRrx1GWDZLTKElOXKimShEz3uXBNyTjrppFIqE7gGeCwkRnH1asZRd2IKeDa4hjWTUOLDSpY9LHbLApY4JUOZOBvQbuCDZhTE1JB12XwsV6K/aC75JEkWj5HFVbZowNJZTcRzNafQTi8Gsk8LpSKLnrCl+X5kC/NGENZNN920NIAgvARRchJ4LcztJXp+l+WpBKstrT2GpxNSmcEad7BouXy5jGUSi+MaSSeRSmyXRcyqJfJ6HKud9fMkSZJZZmRxVZMoAQViaJD0YiGUCANxPMkx48DiEdcTsxP/k1U6SWQ8h6t7EDbaaKNiyS06+goTQclIMnhNNtKA32dNPMWpfS4yjQmvdobcxLKH/SutXbZwzU9/+tNS0+oz9fzaL7JKuZ332muvEssnsp6LZ4SVy42sU5OvlfwQcK0VueZdX0mSJLPIyOIqS7TZIIK4slw8oPj/E5/4RKl3HAVdn1hPhBXnnXfeqIfbFZnOk+7MsSiIqYt52iyxZFmoMYqOBctqVboj5kpoL7roouIyJ5JEsVtLSb8rlMA65QlQO8vy1WhCLJuFqxGJGbIaV3jNaDzh9XTFklilzWKSJMkssuqplwR3VAifebCzhMV9meC+JaLcwMpi1JuKxZoNKw6qWb9NFveu+KjyGTFUU2648dsg2H7P3xFO2caEVsMIGyhxXH/PM6J+VgZyxH8/+MEPljABcWf1qrFOkiSZNYYWV25UY+QGgdtu1PaH3IvckrOGRX6ZIJAEjtCJf3LVisEqiREaOP/88zv3ve99O0996lNLzFQsnpuXBcuFq4SnDd4NU3AkJ3lOwslCliGsPEdmMmtWFycCHHhusVfiy00syenOd77zWp2OJEmSgRhaXNcqU9PCqtm75KFwC68GRHxQxBrVXS4bD3zgA4vIsdoJmsHmkpt+8pOfFJe/Ga6aQLA+NYbgyjeQXTenbrBGxU7FWg0DMAtWPParX/1qcRsrj5JRzL0cJUEQ8+V21mLT63FXi78mSZLMEkOLK2uyrVFAG+ohJTgNU/jPzahDTwir1npaDfZDsowkGh2FAhnG/SASg0JUlrWJge5byq1YlMpklN5wDYudsjhZlASPQHLbRtlOL772ta+tTNnh5tU8gkVLXCUxsZQ9t/8HNkM6Nfme19PbmEt6WT+XJElmk6FXJItabUn047a3ve1Qw9KPO+64lYxgjSmIcyDBydQdHZKaqK2UUXrdddcN/FrJ4CihEXvlypVsFC57LmLWLNeu3sTKali5hFJTCe7iQeBO5uLVlMI1QMjFXrVjvPjii0vtaw2rlUfD564+VhepJEmSWWFVt/videJxw1BP2LnmmmtKDC5g6cgulZXahHvRYsvyrZ/LzFmJL+NiUozM1WWHADqnEot4F9SlElYWrPN96aWXlg0RUWXhyvjVXGIQlOawSrVZJOI6N+lhTahZytdff/16v+/nyn5Y1f71dZIkySwwMXE181MCS50hyo26ySabDPU8BKyuO7388stXXL0WXHWQ3Wgmtmy88cblX1ZOG2KFXJiDINbs9Zcdblrdm8Q9NXRQDuMzUbbjc1L/6lzJLOZF4NqV6GSkUz+49iO+HqPujK5TS+u6aI6DUg+rdEeSmc5O3MmENkmSZNoMLa5qES2uwXe/+91SbmNhtSDWszdlmEYnn0HRa7Zun8fVKLYH8TWlIZNCfeug8eOo3U1+2e6SK5ZL2L8EV0cmpTgSjpTiEEOlNfoCs3RZs8SzH2LgvB1isOpnuXs1D2EJc0cTbdnEXM6nnXZaueYIO+tWMpW66hyuniTJtBlaXDVP9wjEUy2aElPExmKwNix0P/zhD8c6QC5FcVbizSU8DbgkjWBLfomxglH7qkxGxjDr1Sg5FmS4z21IJKVx9+pq1a0sp8a1pO1hzHg1pm7bbbctmcq+xzol5CxnyVWsZ72KuaD9jMDbhCVJkkyTsd3CpuCIja5WQom+xRZwsdRplcEQ12Fjx4uONpAsxic84Qml1zD3MEuWS1+DCGh/GM0nxEMlRQ0yNUlnJ8Iprku4TdD51Kc+VQYGKIfShlEmup9z+es1zJJVlkPYlfNor5gkSTIthhZXWZssVNZFINHEglajPZ2+tJNgtQYDSL4ZhK222mpVXn/e4fZX/qSZhJaIYtwsWIJnLiwIrGtDLF7tq2unLq3phhIs1qnnlzjFg6G/sZpWGcSElAXNJe1rYix5iofhMY95zMx19kqSZLkYWlxZIm2lOOoM1aeuW7eufK021ciwWabeIPRCqUnSDlctYSNoEtoIriQ0yUcxGUcYQQcm1ibxtVnqNve1hqCecsop5TUkKrGKtVzkydB/mGtaspSQgfisrk3CFOpeuZTFfm9yk5us9ilIkiTZgIllC8uktXiefvrpK99T48ramGeU8Yw72WeRkRHOQ0FgiRsLluuXIEbjfu0T9RPWsUlvYpswmdr9BiZotSluL0mO+1lZ1n/9138VF308B2tYTP6GG24osVYuZBnEkqhuetOblib/SZIka83ExPV73/veBm5g1sMwDSdmEY3hN9tss2kfxkwjkUhZDGHz/4997GOlHtbXUZMsuYmrF+G6ZXX2Qx9hn4Gs4/3337+IqevMpofbWLMJ1xmh1TJTTFb83wAAmeVeK8tzkiRZa1a1iUTd0CFZXLheWYusVW0P9QRWPsV9q8+wmOuZZ55ZynEik9j/WZbvfOc7ez63zRnB5mr2nBpM+DuuZhasGlcuaFnFRFbpluQqcVrC+8IXvrAkPpk5myRJslYMLa5qDQepV4RFcN7JiSuDI6taTFV5DLetbkuaSEQ/aoLIstTtSsKbmKrm/+pmeyGmqrUlF+9uu+1WSns233zzIqTKe5QAEWAdomQSGzTAcnYc4v4saZnNSZIkkG+jNr7GOjJJhhZXFoJRcsMIpyYTxtTNo9gefPDB0z6EuYEFy2WreYTkJlYjAeSiZVXqFS02yz2s0YPSqujeRAB7zf5997vfXSxSzyeuLyFKHJZFStCV6fisxGhZsyxkiVMEWb9i7uVMbkqSBOrvm93+Bh2lOihDi6s2hywPtYWSRvqh25LMTgOx7RTamu4ni4WaVFnlHlogcv1KbiO8uipFwwfYqBFjPYrf8573dH1ObREf8pCHFNez+KryH3/jaxnEn/vc54obWNKT0hxJTqxnjUckTvmZv8vuTUmSSLzkNatR9tdssToOQ4sry0ONIUtgkGk3rBLJTsojxONmBUO+++1UvEebiWQ4JBEdc8wxnd/93d8tGzCbKxak2KfJRlomajxRD54XT2Vp9orBqkv2nOpZiaSWiNw7SqV0cPLQ25joukYlQBFUzyvuK+tY687b3e52a3EakiRZYoYWV+0NufC42nRm4urrBjechdYgbQks4myzgkW4uXNpYhGeR1f2LKDsRtYu61UsVocm1w3Bc82oQeXS3XPPPcvv697ETSOmr1l/N2Qfx8AAO01doSQ52QSxfPfbb79irZ599tnFIia45vpqZuG5NboYpMY2SZJkHEbKFmY9eCjqt1BZxH70ox+VRCe1rvrIWjj1eVUeMY9wV3ofyejsvPPOJaEpGv2bzyqDWNyeu5jg+jlvCLQsJIDRP7gN35cIpWe1ch4WMDFVU0tgxWRZsqxkzf95H5QBGVcISU86SIWoJ0mSrAZjleJoaechKYVFq7WdRSviafOMZJucDzo+sne5cZXkiI+yaMVHXSNir2pVxeLFQEB4DUtn8WoM0YayHg9xWNedOL6sYaLK/ayhCWGVIEVsCS9rF/ocs3SV9iRJkqwWE6tznVcLtRtEIJkMegmzIAnspz/96bIhY0HyfojBsjxNVdInGFpoipVqpRizfNvQZ5hoSmCSvKT7k+dgJaux1niCQBvmLmNZnB0aXmgwwevCQ5EkSTJpRhZXjdnFvPQQZp3UmPEqNqY13rzWiUrASiaDhCKtEWWM69p0/PHHFxcxUZXIpAZWEhJBJLhQnyp+yr3bDZnHrFBhCZsh7l5Jakp0fJ+w8j4Y3h7WsSxir8PbIqYu9istP0mSZJKMLK7f+ta3SlOAtnIcLjvxMD+PjjzJcsNVy+XLKhVjZbm6PmQAEz4Z5YTQz2NDxiL1fe7kbnD5SpLiXpYNzIK94x3vWMpzDFm3CZRMJ9arDpYARxMUsVsua5nFcgWSJEkmxdhuYXWssj9rC5X7b++99y61sPe5z33K10kiI1iMlNtWfFRs1eYrOqWwKo33k6wE9dSyuu90pzv1fF6bOZYul7M4rvIc4opwOWv4T3y5hg8//PCVv/X7+hUPOiEpSZJkEMYWVyUPpsY0u9/I6mSpKPyfNbgLWSzdsKinq3D1MH5up512KtcNq1ESHBcvfDZKtiQc2bCxQn1P9rma6W7Y5NnEia9KahJ75VJWBiS5iUuYBStzmBVdd97imvYa/dowJkmSDMpEEppMKGnWsFoMWQOz2BGHq5GV0w0LMss7WR3M/jUeTkISQTznnHOK2EpugrIu9almtPq+zG0dmVi7119/fdfnJbC8JZ7TtcctTDi5isV1lf0YsK4to0xj/YchTqtGVi9k4pskSTIuI4urBVIyk6kl+r5mW8NkGMRdZRFz1apVlb0rQS4gfgTVtQWxUqIr67gXhquLs8pe54L2/JKoiC53M4E2wcfXYrmRjaxsx3AAbRK32Wab1XvjSZIsBSOL6yabbFJ6yHL96sSTDe6TYXnkIx9ZGu0LHbBUm0hC+tKXvrRSFiVxSfkMS7cXXP42f4hWiBpaqIXVlpGIEnbxVrHaEFgtEh2TGLDYb5IkyaiM5RbmOpUo0it+OY8oG0nWBpuzE044oQhnEw33JSbJBDZqjrvehq5fj2qWqxiudovcz8pu3vGOd5Sf+Z4GFvoaH3XUUeX61bBi9913L+08Wb5eU9ggvTFJkozK2DFXszM9ZgkxtLB6hoVFns361xZits8++xQLswlXLjH0eRJAsXxJS2Kk5557bs/n5UrWP9qcRrFU7RW33XbbUgbE/cuqVe7DmpUAteuuu5YaWWLvNWUz+/0kSZJhmViHplmC5dmc1TcoFnDDBpK1hVgapN5W06opCfHTLIK3RPnOE5/4xGJ9KsPpRpT0yFyP5hVbbrllKQ/zOqxmg9xlER977LHlc9ea0fOK7fobXhnj8pIkSYZhIcWVC9FwbpZr2wSU6DObzA5qWSUgcQ9rDNFET2D1sWK0NkCSkkxmYmHquNQPzSq4f4mqjk0sUoMlCLVaWEJq0o6h62KxOkUZTyfZSrZxDlpPkmQYFlJcWTceG220Uau4Rk1lMluoLyZ2xvydeOKJ5XvctyxXsVACG/2JCaz2iK9//esH9lLIQJbARGBlBOs9LH7LPSyJSemPSUjmxBJxv3/ggQeWGljZxUmSJIOykOKazC9csho+iH2KebIyZaIfdNBBpTex0i+iSmSV6WjuL/tXpu8g1APXQWz1IfacXMKGtRN4FjSB9TW3MddyTklKkmRQUlyTmUMHJS0LxUTf9ra3lYQjWb2aQsgc1khC1i9XsixgliiBJJgyhfthqMQb3vCG0vbQUIHXvva1xbXMbSz26mdXXnllieuapkNo//zP/7z0Hyby6SJOkqQfKa4NchrObCBjm0tW0weDzgkowdV84otf/GL5HaLr89I+UXcmpTNcuf1gherSpL0iF7Cex6xTwygkThl3x9XMJS2swJJVzmMYBeHnTua6TpIk6UaKawOzRpPZQNcmYqbLkgQ1wseCNCYO6lKJLeGVxEYUJTgNOghdGQ4rVDcnYknMlfxoJOFfcViJTv/7v/9bBPZVr3pV+Vfzf1nG97rXvVbz7SdJMsekuCYzjZgqAWRhEk5xUJNyxFklpkl20j+YuBI7rlxJToOgjIcLWIeozTbbrLPXXnuVWlsxWZaq59W0gstZ60XTdLilxWH9HvFV1pMkSdIkxbVCeYds0WR2+LVf+7Uy1UbNKqtRrJVLl9AqkSF2p556amlvqDex3xE/Nat1EMRpCbLn1aBClrlpOqxZw9S1TNQq0aQdQyg++tGPlp9JtpJUJRZ8z3vec5XPQpIkq8V///d/l0RJeRaTJMW1gsViakoye3AF67z1kpe8pHTREg/VVIIoSkjSgEJJjQxiQ9iJsZ995zvf6fvcxFnSEsFUviWRSlkOl7N4LFc0gZXBzE3tNXR/Ug/LbcyKzU5OSTKfHHrooaUnAoGdJCmuydwgBqvGlZAac0gMNX2QjCQGGr9D7LhutVRkZQ4CFzG3r17E8LdiuUp0vI7GFixl9a5ElwVL4H1fjNbvaq+YJMl8IdQEni95FZMixTWZK2TvXnbZZcWVQ1jFRLlm9Sdmgcr4ZXmqWRWvlVk86CAG8VeWK6uUi1gMlnWqgxN3s5/b4ZoxyzUdr0tgZSrLXI4ReUmSLDcprslcoUSHJSnZiDuH8MkS1oz/2c9+drFsJTmpWRUTFXu9+OKLS/ZvP7idX/rSlxbBZplKclLmw0XM9fziF7+4tM5kORNaqIvVlpEIa5V461vfuriwCXCSJMtLimuFusdk9tE8QnyVoJ511lnFLctS/cAHPlD6A4vFirX62hB0TfjPOOOMgeKvYAH7W00mwBLefvvtO+vWrSsxV9azOCw3Mne0+luuaNat8h6WtXiveG2SJMtJiuv/j3IPyTLJfKAnsFgJC1UXJbFR1qOOTXvssUcZMQeZv2KkxI84DtLBCZr6S1LSOAI2XhpUEFf/El7lOV6X0HqYN+t4WMlivVzHjiVJkuUjxTWZWwgsF62WhEpqWJiETeLRxz/+8ZXpOoTPuDmCqBnFt7/97b7PrYuTDGIWqCzhgIATax2h9ClWI+v1vv71r3de85rXFJe1RCevz0XtdbmWkyRZLpZOXC2Kg8TfkvkgOiaJd7JgWZpisCxV4ijpSC9i8VcZxEpq9Cg2YWcQiPeNN964knXMEj3qqKPK11zCWjBKnNK4Qn0tV3HEZcV+1eOyprmub3/726/mqUiSZIZYOnHlFuTOa6L1XTJ/3OxmNyvufBaidoiyiAms7klEjuUp5qqGjQh6iIvW1mgvjJuTKKWZhTaM2HfffcvsWc0nCKZuTkbk6YMsoUnik6xhrmWC7+8kPbGaU2CTZDlYOnHtRnbZmV+0PYyOSdyzsoNZjCxUI+yIrHF1SnIi4WgYCLP6WQlKng8EVkKVUhx9icV4NbfwuqbnaPyvwYTyHAIvyeqnP/1p5z3veU/p/JQkyWKT4posBLJ5jacjfkTte9/7XrE4r7vuuiJsOm8deeSR5cFlOyy8HaxdLmfuZhjYLktZElOMvlOIrtGE+bIsWa/NWv3BD35Q4rAeRFncNkmSxSXFNVkYxDWf85znlFKZE044oQidWCy3rCQmCVCEVwx1VJT6SJ6KiTiSlaLWVVMLsV5uYlYzF7HuUSxnzf8JPbiTWbB6JidJspjMtLjKtjzssMNKr1i1jdtss820DymZYbhjNXtQ28qCZaUSN/9nLZ500knFqpTxOyqyiPWglqEcs3+1SpQ4JWGKdUvQuYLF8bmAX/GKV5REKrW5am2NsJPBLJ5rqk5mEyfJ4jGT4mrRUUZh8dLO7oEPfGDnHve4R6lrNP1kHCxyTbgMWTTJ/HOrW92qdGVyDbEeWbFvfOMbi+tW5yWfv/F13LmE94ILLiiJRsMgSUn5DSvV3xJQluzf/u3floEB4rOaUHhwVevmJCYrs5j72Pd9bXQewfc9x5oD2JNkcZhJcTWrUwF+jXFA6geV0ey4444jP/fZZ5+9wfc0BkireHGQQfzP//zPnQMOOKA8tDLU1tAGjWUr7ukaI3Cs3FEgoty9al0lU2288cbldcMlrC8xt69ynbe+9a1lIIDsYRtFbmnWrc5ORP4v/uIvSutFgp0kyWIwc+KqVtAOH8985jOL1WHxUkIhE5SlMY64JssDgVUHqzewa4j1+vKXv7xcP8plWLKnnHJK+V2uWcPXh8VgAFnKEp30Igb3sA3bW97yltJj2DHogUzQJT1JctJ/WKYxAWYBi8mqx+W2TpJk/pk5ceUa4/79xje+0dliiy2Km88CdYtb3KLEqpJkUFxLYpsPe9jDShmNVogm3rAQuYZt4gxbZznK/CV0YqniqsNgXB2LlDtYza3XZSF7PglWl1xySRFWr0uIvaaSoNve9rblGPzra6/NymYRZ2lYksw3MyeuMPnEA0og1A6qNbSASR4ZFS44brwm3HjJYiJhiNXILSt7V4xUQpMyGaJGZGP4ueziI444orhsTz/99GJJDsoVV1xRrGKvoWkFMSfYnkv/Ye5ngushq1nc1TGxYCVc+X2NKby+7GY5AITapjJJkvljJsW1hgvtoosuKv+XgBKutzYsYCxeLejAYqi5+uqrW6fNq5FMFhetCTWWkLUrtklEeUW4ZcNVKw6rycRXvvKVYoESSKI8DEIaLNVzzz23xHi33HLLkuikWxSLlVXKUiXwYrKE1f9t+LiOJTbpf8zy1bNYbFamvO5QSZLMFzMtrlrZSUiB3fyuu+7a8/dNMVG8nyQ1QgtirizGQw45pDR0kFGsZaEkOSKrfSLhE/vknlU2Q3Qf97jHDR2OEOv1ekrJtttuu2I9K9VhjaqF9VosZR4ZVrOf2TgaPOBYWLReWz0sweVx6XftJ0kyW8ysuFqYnv70p5cMTIvQq1/96r5/I25liHag1+yXvvSl1TzMZI6Q2GSzxv3KMhViYGVy1YrLioXK9uWKVbLjX+LnmorEp0H52te+VhKoWK02fWKoEqgIvFpYFqvkJfFVAs9Dw1Xs9WUYq9HlIpZpzOp1P6TAJsn8MJPiqpuOBU92sKxLbl6xVz1ht9pqq65/ZxHyCLjhdM4JauFNlg8xVuLFHWvDpovT5ptvXupQuXSJoQYRrjcCaHPH6lWrypokhMNw+eWXl9eR2CQey0XMIo06V25obRAlXRF9YnrwwQeXGl3xVhN4iKzjsRl4wAMeUISXWCdJMtvMnLha5Cw4Z5xxRvlaPeEOO+xQ/q8xuk47o+7gxd2S5UY9KqtUG0PXmYQmnZTEXoUeCKnrROyTENqsEUMNH5TriKW2TVXqhg2hjaIB62q3CaSYrziq177//e9fBNX1boydDaG5sJLsHB9hlnwlDsyKliTleLiXdaRKkmQ2mTlxhYzLNriIJ509Kekkyx6WCxasZiSnnnpqETCzXVmm3Ma6L2nuQFxl8V511VUlhkqACaRGEKbbaG84THw/mvazjiU9Sa5SmiP26/nFVcV7WaZ3vOMdy7/itkRfQhaRJ873ve99y4QfAsyd7Hcz2z1JZo+ZE1eZkhqhs1ib/Pqv/3rnDne4w0Rfj9tY0kmyfMjY1fyBxWrOr6QiXhJuWA0gCJz2hFy4Yp4SkoghC5LV+KpXvWro1yTqEphYzxKWIuTBQj3nnHOK0BJLlrUcghi+7nXFb1m22oLKiifO7hVxYy5s9eBJkvRHbXpz9OT5558/0deYOXEFy7Wb9TppRhk/liwO69atKy5fHcDE98VGCacY52677VbcsTKGiS1x83vKZrh2NTthhUpeGgZi6nmjhvvOd75zEVsC6SF5T7tPVvJPfvKTMvxdJjEB5g72OzaFhNjrE9+jjjqqPIc4Lcs8SZLu2Cy711eTmRTXJFlLCBeXrYxhu1eitssuu6yMk+MmZr3K9JXxa1yc2Ktwgr/jImZZEsJBMW9WOY4YqufkkWERE2yxV8dAxFnP2ilKwpLc5PVYzJKfxGz9q192TOSJ8p1sPpEk3ZEwKCRYY4Pq/psUSyOuMkOzfWLSDS5iMU6WpO5M3Lf3u9/9yg1I6O5973sX6/WhD31oSXSS3St+yjXLeiSMsn+HLf2SyGScotiqrGH1tbKBuaA32mijsgi4dsV8WbpqcP1fzJWga3oRry8mKyGLS9n3bBqSJNkQ4UfhoBqJjCmuI6BhQIpr0gsCq4uXZCPuV3WvBBasQpYr0WOxSngievvuu28JLfieWlW731FisQRT8hRrdu+99y7WLNevRCuC72uCToQ1+if42ipKuvKafkf9LnEVq/W152Fx2wQkSbK2LI24JskgiFcqnQGBImRcxLjlLW9ZhEw81pzYm9zkJsWalTXsX0InAYl7mfWrE9SgyED2uhKW1OLqo80dLbbLFcy61VCCdez5Can+237fhB87bnFctdzPfvazV8baEWhzZg0nSJJk7UhxTZIGmugrf+GGZbESTUlGGkoofVGyw5IksgRMzJUIsz4JnFitsjE1tdddd91Qr60fthaIki08P+vYv0RUbaykJa5ixySuatKP7GOtGwmxmCshJbjcXv6O+1jLRcfFypZAlSTJ6rIU4moBkkDSxGKTC03ShrIv1qkYqJnC//M//1MsyUB9rIfm/jvvvHMRtec///nlIS5roo6YJ3EcBWIuG5hYR1awWleJS8TXa6qN1VFKspMG/7KaCamMZtYr9zS3sLnI/o4os2w9p4SsJElWj6UQVwkobRiazRJJkm7IxmUFireyFsVVWaUBl61hADKIuW1Zr2K1ymdGFdZAc4tDDz20DLBgHXtebmdZw8F3vvOdEpf1O7KLiSnXNkHVD1mSk+Mm+jqbEV/1vJKlJGMlSbI6LIW4JsmocMXK3iVukpvUmLL+1MRC3JWFyBoUKyXCSmS+8IUvlN8jfOPC5StbWQ9kYh9lOtzB0YpR3R4xVYbDkmXdsk4JqJGNMojV9Eb7RW5vcWLuZ7Hl3GQmyWRJcU2SAdDFiwdE9yQuWsIUAou73e1uJctY030WK9HzexKLWLvcyuMgaYqwc1XrIiXGy9VLJA0IgK5m3ME2BLKabQjEjFm7YrWSsWwUJDhxd3Mjs8odH+HOgQBJMjmWWlzVOiXJIEgeIljRBlFcU4MHJTuB64lIEULlLzJ6ldZoRCEmawTiMI0mmnABi7FC0hKrk3jKCGa1yjiWoaw9Ihew39G9SWxWlrG+xKzWqNvVK/mKK64osWM/Y/GK9UrEygHtSTIeSy2uElWSZBgMPtfuUNxS4hLhajZr2HrrrUtBuuk1ak65al1r6lTVpn7xi18c+zjUu3qYFEXw9RUmjCxboxr1TvXgsjY3VlMMCU2aTtzlLncp/xeH3WKLLcqwAlaumDH3MOuXO5kAJ0kyGkstrkkyKhKXWKqsRwlEkSVcY8oNq/Azn/lMsSIJ7Pe///3ijv3Wt77VOfnkk8c+Dg38xVe5qAmsxCqua72JwTIlloYCsLIlPBF8LmXWrOPXhYpFLBvZ8fk+y1xvZd/zdxKgkiQZnBTXJBkBGcPmrHLLKsfx4BLWwrDmdre7XcnWNaeYFakDlKHpBFZ81teEdhyUmXl4LngdsVTZxvDaYekSfJa0pCslahKuxINlETt2GwXvQxtHIq2tItG2efC3SZIMRoprkozBXe9611KOI74qlqkzk76/m2666XoxfTFXcVjuV9ajqU8x5YbIKa/5+c9/PvbxSHTSMMJrcP8STW0VA65q1q6NAetbfDZqdOtjN8T9rLPOKr9/2GGHlUYWei+zvsWf12pqVZLMKymuSTImm2++eYlh6jcs2cnXEofUv9YQJB2SPPQAFuMkfn6XxcglOwnMptVUIuDyZcVKeoJ6WQ+wYpUNSbpyPI5dYhPxleTEWvXQlSpismLKkrkIbpIk7aS4JsmE0NVJW0QixiIU//Q1kWrCapRJzDJUH3uPe9yjWI/f/e53Sw3rJDGHltV88MEHF+s0hBVEUtyVgH7yk58sx66lo9aJ3MFirmp3WdkaY4gfa6noOTS4YMlycaclmyTrs7TiajHLcoNk0uhLHFnErFMNGsRjxTabAhSdlPbff/8Sl5X0pJ4WSmkuuOCCUrs6Lp5DLavm/8psali5Snw0vCC82iqyZiVCicHaADgmbma1sQTWw4Qplrk4LosW5tCyeJMkWWJxVWpw85vffNqHkSwoyliU62giQazEU7l/lc40ERtlDbIelfBA3JPAavwgRjoJJE51S55yfFG+oxZXnFWJj39Z1ixtsVbZz7e//e3LhKBwPWtS4b2yvA03YOma2MOST5JlZWnFNUlWG2LENcy9qiuSpCebOoLVbGAiMcrMYZYkoVKzSsQ0iGABryWO2WOfffYpSUyOmYXKMmXZGnmnZlfWM8SbdY9S3iPDGNzixNZ7T5JlJMU1SVYZcU0uX9Nt/umf/qmUuXCzchk34U3R9EHrRPFMpTDT4qSTTipuZAlMjklLR4KpUYUNgH7FhHePPfYo06W0fzQoQJaxch51sjYRXOJiuHe4wx2m9l6SZK1ZSHEVq9KlRuF8kswCrFjZtTJ3ZQuLZXKd+prwNPv6crtqvB/1qCxIMVHxUwlERx99dOcXv/jFqh+32KoOTuKt3L8EXyxW4hUL3CZBljPLmwWrW5VB7wbM63kcPZD1YnYOHDurNqzeJFlUFk5cxafsqM8999yuv6MBQHacSaaBmKvsXc39CZVuSNzFsorb2g0aCMAa9GD5chd/4hOfWPm5RCh1tquNOKzWiUqNCKiuTuLB3/72t8v3lRRxF/u5GllCq1Wkh/vRRpcgyzCWIb399tuv1OFqtJEki8bCiavFyy6ZuJpxKXbU9jtGhCXJtCBQHsbGuV4f/ehHl6k7XLDdstjVn4rBmnADDR/WQlib2Bh4XHbZZWUmsodsZMfFfWyjwHvkvTjGu9/97uUBlrj3oJkGLr300lKqRHRzw5ssEgsnroiFSwZmm7gmyaygL7AHcXnIQx5SsnnFKG3+lPU0YeVFuYt/o61hL0/NamFj4IHNNtusc9BBB5U6WXFjHadYtq997WvL+7nnPe9ZWkWCEIOXiatZDFps1/vZaqutOrvvvnuJ4ybJPLOQ4pok84YyHWUu+gKLUXIZ6/jE7Sue2Q2JUizB66+/viQUmdgj63itMU5P4hbrU0tHCVmaVhBS7mzj7Qit98lKZ53zIHGLi9led911Kx2rvBfP4/cNEEiS1URfblnuGqRMkqUUVzWESTJriFUec8wxpYEDUdF8X2auZCJxy24iqyWhx3vf+94iTESOa/ab3/zmGr+DXy5ULFb9jR/wgAeUmlcZ0o5LzFX/ZW5wMVcLmvcki1jZkQ0F17dBApK5ZBwTZuy1117lPIj1Jskkkfx60UUXTbzvwVKKq7hQkswqZqyedtppxZIjMkSWQBFM4tKska3R9emII44o5TCE+f3vf3/nxz/+cRmkvpYY2q5LlYfMYDWzamFj2o7GFOp3ZRYbiSeLWDZxJEHJjOY21pLRQ+mPtozaMbLm161bVxpWZJe1ZFxs9CTc8arwHE2KpRTXJJkHxCA9lOGw9rbZZptSxiKrmOD2EhalMMTVQymPmKxGFmstsmAVeLBC9Tjee++9iyvbAHfiykrfYYcdSocqAqu8B9zGLFkPcCGzxrm/DZznNmf1yv6XTZ0ks0SKa5LMOEpcWH4ERQ9gFhyx5WKVKNTWjKKGeHlwF4t9EllW8DQgqB4gihpTEE0u4y9/+ctF/F//+teXn2tYIctYNrINheOHMh+Z1TKljdPTulFZj+5R6oe591jCSTJNUlyTZA6QOUxgPcRkjZBT5sL9y1UsiUiiEBHiGm5DFyUPnZPOPvvskvikZpbgcuOuNYT07W9/e/m/mLFsaYLqPXKHyz4GgTVzlrULQzf8P74mrmeccUZ5T+K2krpsIGQdR0KU5yDASbJWpLgmyZwhJuuh+5GYJuuNi1R2LZHlVtXMoRu6P+25557lwb1sfJzn0EGKJTkNTOZROudRo/SIO1wWsQckSilVYp1KhDIgIN6Pdoynnnpq6Q5lTi2rXzYyN7mNB9GW0NicDpQkkybFNUnmGNYetFTkKpb4Q3SILZTqqEHtBUGGFozEGpo8cNNOGxZ1PX8W3OMeBFbryMggZumy2mUWe/gZS1gWNYit5BVxWiIMgivWmySTJsU1SRYEtaUycYmJ0XFf/epXi5tUlu797ne/krUrgagbIUogzsqCJFOBwF155ZVr8j6GQTZ0IHbLZRwJUZK/uIPFpqGFo17Jkrx0kILzpFeyRKpodrHvvvuu/RtJFo4U1yRZIJSnEAsPjRnEVaMd6Pnnn186l7FmoTNUN7iO1dZ6QJyXe5Ul+LOf/WylV/AsYaiB92gzAVa8siX1sZKiwGoNqx7ek/cmo1pXKSP/brjhhs5tbnObEtOGhhY2J0kyDCmuSbKgiCs+9rGPLQ8ce+yxxWLjQoamFeAi5RIW3+zW31eMF9HFRlxTUlVYiURJ84dZwjQfsOgD5T2sc9OIlARhu+22Wxn8fvXVVxdrlvUf54mrOaYW8QTc5CY3Kf8n1EQ4SdpIcU2SJeExj3lMeUQTFaLL9RtTdmQRE89u2cY14T6OfsF6ImvfKK45y2hM4f3Wk4WU+LByYQqRR13KI9lLG0ebk7pD1EMf+tCVYfCSwbJ7VFKT4pokS4o6UWUs+PCHP1y6QmlHeOONN5Z4JctWDHeQtnB3utOdyt/H8xErMVqdlnRlmmW4zaMkyIzaW9/61uX/hgc4B5tvvnlxhz/3uc8t74+72Kg9iOGaBiTeq6mHLO06U1sGs0zlZPlIcU2SJYV7M1ycMmsju1b9qfijZg9aFBIU7uJDDjmkNKzo1hmqfr7omKTEJmKzYsCm/8A0nWmV/TQxdD46V9WtUdXecv0anadFY8DC9zDsHnHOJFdxKUeTDG0nnbMo+/F8L3/5y9d7beP2iHeyeCyduCrGH8TtlSTLSLg2o8eqLGHCoSE/EVE3ak6yDNw6bgn1o+pOa2KoQKA2FyeddNKKuCr/4XKtueSSS0ri1DSxMfBwLDpC1bBoiatSKK52POlJTyqPwPGL4eLiiy/uvOMd7yjnsMZ5Jq5KjkwW6obNTTbBmC+WTlzdFJp/J0nSn6iBRWQOSwoSryW6mp0fffTR5f+a6UsOggQoblTZum2DBnRhCtyPymBqzGFm+UHjfrFgFqZymlkgXN2f/vSnuw4CkbltODyUQbXVDWsBCTFr1rxMZY0uaiSLqc91znTYMsqvG7wKmmok02fpxDVJkvFgaSn1QfxrBu1ll11W4q4nn3xy+Z7uT+KP0ehCkhAX6yAccMABK/+P12BBmqYD7Q1nHZa58xLYbDRh6SoDUl/rgdq6VSq03377FXezMiP0mtyirvc///M/S3OMZLqkuCZJMjYhgOa2EgSoO+U+1vcX4rjirjX6A0fmseYNEcdsQxvEaOpvWlAT03LqHslczbNi6XZDIllsRpoQ2wMPPHC9DluEV3azEYSvfvWrV77PY8C6PeGEE4pXwRSiZLqkuCZJMjHkM9Q5DdooBl/5yldWsmwDvYRl6IrpqrNtxmxNuYkGDp43LF/lMk3e/e53r/e1Wty2EXtcsF4zYBHbCEwDru6IyzbxfU1AasRtWbHNv2Ele182E/oqR5cpVm52nJoOMyuudnPmPwaadess02tQ9CDIiEySZO0xBL2JOC2U7Yg51nAz165U8cawcttgyRHoQBlMt8zmqM8FN6r6V4ilRi9isIQJ4KygTOrzn//8Bt83CcgjiN+RnR39opO1ZSbF1Y7zkY985HouHjMsIwV+HMb9+yRJJo+ewNERqSZKd0Bsa+Hj+vzQhz608rU1osbcVz2DuZ57xSDrulTH8Na3vnXla5OGJBQ1ed/73te59NJL+7yrZJmZOXHl1hDA5+aQ1CC7lwUr/V8WXbRfS5Jkudhqq61K3WhgrTA8vgnhMzUnXKdKhvq1ZiTC6lObPYSbmbuB2GdbPFf2cJTtsDJrt3iyXMycuCLq3+wixQsUoRNXrhsxm15JD0mSLAdKTjR5aNJMdmJhiun2QqclSVltMdo2hKii7KhGtu4zn/nM8n8uaRnTbYiFqqGFTcAsThxKxmPmxFUrsW5oxK2oPertkiRJ+hElLv1QWxvN/nuh/WGz01IbBFv/4TZYypEFXIe/Jo2EsGQ6zJy4nn322dM+hCRJlhBx2UHqQ5/4xCcO9HyGIlx44YUrX/PARSnRWsA61q4ymQ4zJ66jotl2M6uvrX2abMPof5okSbJWxFCDtUIy1uGHH76mrznPTLomeubEVQLBP/zDP7T+TLJBt52YOYtHHXXUet8TozXUeYcddih9T6eFEgOTMeoygbXEReMYdMoZt5RpVDQS0M4uSi+mwde//vVSa+k6MsVlGugxK772wAc+sLTHmwYSbZS6SRycFqecckrJrWApttWsrgU+B5+HMr9orr/WuB5dl/oGa+I/DSR/RXOPBz/4wSstGYeBazuahYzyHBLOzj333DKBaVp1uWLzMtInxcyJq4tMo2/BfslL3/zmN1emami6302gJBFEIkGgQF0a/kEHHVRGaE0LC7n0/mmVATmPjsEMy2kJvE2R3qrHHXfcVF4fss6NUFPeEc3W1xpDuT2UlMh+nQYWEM0YpvlZcI8a86bGVBLQNHAejJXTSvFBD3rQVI6BsO26664lw7nu47yWeG3r45Of/ORSzjRKb2JduaLTlF7Rw4rrBz7wgdKDwFpdd55aS/TJ7tVaclhmTlx9KOrTXvCCF5TsPaJwwQUXlJ91Kwifdbhm1PEtM7rnNCeLLCOyR4UmpiWss4JWfTZ60xJW+Axs2KeJxhrCVM7HtIjX1l5y1Kb/OmvpTTAqvAcmMk3zPEyamRNXqCEzwPiqq65aaZcm7V2D63nkGc94xlRf3wKiH+kgQ69XC275pz3taVN7/Vlimq7xWcFCPM5ivCgIDUx7tN4ssO22207UJTsLzKS4QtxVc+qA2A67y5Xqzv237MOIJXu96U1vmvZhTB3eA9ZKzsVMkl/B6nRftNXtJqMzs+I6iZ2tpBHp8EkCCTxifNxfywwvQnY6+yW8Ycs+no2w5n3xy97VkspuectbTuT5ZlZck2Q1WPYFBMIEMWN12ek1CGCZyPui03nWs55VHpMixTVJkiRJJkyKa5IkSZJMmLkUV1nE11xzTed1r3td59prr+087nGPK/2GBy13UVt24IEHFpeQusd5DuQbuxVNyRXCy7ob5Tk22mijziabbDLho1s7XAcxz1KjDKn9g6JF3bve9a7iLn30ox9dyiPqgd/zhNpVjRHUThpwMWhfXbin3Fvwd/M6IEPzfXNZAy7Ptgb/g2CtcD1Mq+HHuGjuEKWMcJ/f6173GuhvY52t2X333Sd6fGtJNLnwWQ7TsEMNb93GUhMavaH7MXfiqoXY3/3d35Xs4eD000/vHHHEEWVAcD+BcNMZlKxJhZOtePkjH/lIZ5999lntQ584p512WhmnFTeATjcKsTUpGASdenTE8v5lVDuP84gFRPJb9KVWq0csFcb3a3V50kknlUYjMZLssMMOK6MO3/GOd0wssWGtMBT7j/7ojzrf+ta3ytfqBv/gD/6gNJnvtxhosKGpg0YfsPE0+cX1NG/15e4HzSECG6YPf/jDQ9W0Wmc0+rD5Vsam0cS8YXDAs5/97M6RRx658j2DBP7t3/6tb1meDbs5tzpIBa6DtW7hOAmU+LgHrPWQHe2cuC4GQRz2/e9//8rX+++/f2ktadPVi7kTVwtHCKssN1YrsbVbdwM1x001+bM/+7Ny4Rx//PGdN7zhDZ2Pf/zj5WSZ5VjfkLPOmWeeWcqM1AETFseuBaTJHhqLm4PbD7/nRoNOWPOITZJFgLC62LVeM+PTNBCLwVOf+tSuf2sz4bPX+s251J7RPE7nUMeeXn87izhe94dNwcEHH1wWAJuFnXbaqWezeZ+9zQRhtaN3f5x66qnl4bxMq6vXKGgl+KhHPar8X8tRHo1PfvKT5X3IiB20/af7yiYLtRU8T9gYWd9Yq3oHvOIVryhZ4ieccELpotQLG+9aWOeZ5zznOZ1PfepT5f+PeMQjylrPwPK9hz3sYT3/9gtf+EK5bnQN9DzOoQoU3pB+G665E9caYrrFFluUN3/++ecXl1g/cYXd25577llOrIvP4kqs5klczzrrrLIA2GB4D3airPcrrriiCE0vcb3hhhvKjRfCOs8QV647EJcXvvCFxZK1M1Urre1itz7CzoMCfn/HcjP4wfVkQZ433vzmNxeLzSLAEyEbWD0vy4uHppe46j2tz++OO+5YNp3CBPPa6MJnp0ctdAQzB5qQEBWenr333rvvc9igDDr5ZpaJ9pbvfOc7S9iM5a7z3Yte9KK+4up3AgIzr6EzGwn6AJ4Y9wmBFFJkpPFY9vJoKN+znlhjGXK8GNqn8hD1Y+7E1UkJuLrEhZwA4toPO1jxB+0VwaWqx+k8dwbh9gwXj90Uce2HhZQ4s85sLMIVOI9ccsklK//XG9X5iBZuLNPLL7+8q7jq5WrhuOtd77ryN/M6Men//u//yuZA3kGU2YQrmDuMl6Yb3j/x0XpUrV/UwHIrT2vQwyRgwat19zmbA+08DCKuFmMhpkUhroP41z3Pwve5d4NLOdDrV/honoyPwOZZDB5aK1orhYvoCAtWPLWbuGq8c/3115f/23ASauGzXvdSzdyJazPAPgwuKu6OwC5/kMD0vCC+wvLoB7Gxq1c8b3c7zzMfuYDHIZI7CBN3MEvYDair1TIRk2l4PVg34Badx/NggyT8I3HFhkGMbVB4M4RXbNpZ9BbfRUPiH0ND7/ZB8Lvi+YwYwz/mESGiYWtYeUFijGkYZBL95DHYbPTLyZg7cU0mwyI1yJ4EQgxPf/rTy/9NxhCTWUZ23nnn4vriFmTBcbPPW2KXrPluYyv7YUPBlczKPe+880rcepkRPhOz51o++uijy+Oxj33stA9rahhLx5K36aqTattIcU2WHj2sYxdvcbUzXWYIqlABgbHbF8ufJ3gfZIKa7zzosApWqg0VK03cXT5DJDKZhSyJRfLbsvChD32otIZk8Xkoy5Gj4Vwso7i6LsSphVyM1nMe+jF34tov/bkXLgoWW2TBcY/88Ic/nNShTZ1Fye4bBlmx44yykylrV879I/lH1uwow6IXiVhQMY+lF5AJKm44qLj6XQso5C3UiZGujde85jULI66SIOUn9EJdZ73Wzls5VhOfofWxfk9cvIOGBSOX4/GPf/zK3Np+zN0qYiC6obYQG7EgRhygWeP61a9+tQSzNSoXd1FS4GSK09mR/8u//EvZkbkBuZLmCen1jlsii1iyi0edYhvi1DLeNJiY14SdbtTJSlLjuXSjqYbPu05WUK7FxVlPV+IKFmckqEo4XDOIa2ZekD/gPTh+CUky4r/xjW+UnzXvi6uvvrrEUuOav/LKK8t95W9Y7RouuF7mHe9fwtopp5xSvpYtGrhfJKloFiKxx33hWooa4SbzeN/43BkPUWYX/1o36mvbxoKhEQ1oJIcq7+PB+Mu//MuSADmvRoi4+21uc5ty/DxUsoUjZCAjvLnuu2bifjEq1O/zasS9FP8OwtyJqwVTXaN4EHH0gKxGQeZAdqCdpgQFxeAyxCAlXXDaQqr8xk3jIhoktXqW8D7sxIiJGj4WhgxAwiFDMrALV3Ikq1acYJ5qFgfBjRDZoDYXhDIWU56K6MTCrSc7XLao3/W5EyFNJGATVlsm//qv/zpXda42Ca4Fi+Thhx9eXKIStFgcL3vZy1Z+j0Xi/pH1GO/dPSIRTo3vP/7jP5aSHFace0qDjXlCtrQGGGp0uYa5iD0spHWewUc/+tFyD8mItpYQFh4Qa0LgmvEz1woPybzhczdDWYKa+8Jn67143zUqKNSHx6bURs19JUFSeEBiT7hB561EybVg0yhWLCnLBis8FHUmvHvAebJ2cH+7P1wTLHxlfc997nNLSZtziEHOw9yJK0tEMS+ifokfnBunbvVmwSWiduD1TXXQQQcVgXGStbFiwU57mPmo2BDoHBJuiq233rqck/o8uIC4M4hKm4vM4sJNNK9TMezAZTy7gaTKh7BKxODiDdwYBFRpTri8pOMvUjYoV6iGKjYGFhKo6auTs1wPLNw4T3AuxFef9KQnFcvXw31mEXIfzROsz2OPPbZk+7JMoaGIjUYN9x6ciwgDqA2v68N5tdxP++67b9nAzhveN3FkfQl9QBnJ8573vJ5/pz7aZsumXKcz8JTJwK437vOCGnafpRh61EAzrrj6A5tQumCNrEXXvcS7wdsZwio/o59bHXMnrrDzVuTOHQoLLNO/SbfdJleyXS3XmItmXiGIRCNq0iyIzR6qdmDE1wLSlvWpFIXrbN4yQmvsxi2otVC6Ieoykhe/+MVlIxW10bCbjd16k3kLE4CVbjFksdhYsmCb/bab10zAQrUB0ybOe7eL5xqfRxw/13fQ1lfY/eB32u6ZQMY0l7kN+byiFarzQVQ0TODmbbLDDjus138YhMam1UP2tF7s89p7nCXOW1W7tpvrPvdxbLab4SAb1ijFgc3HIPXfcymucDJGbabtxPQqoJ4nXDj96CcUgzzHrGNz1bbBCiwWTZc48Z3HOs5e8FLwYHB7dqPt87Zzd0+8+93vXs3DWxNstga5v/v9juvlfe9736QOayrYTPJe9MI107aR8v6FUjzmHYI5SA5F2+84h6PoxdyKa5IkSZLMKimuSZIkSTJhUlyTJEmSZMKMLa5S3mXdDhP/VG/lIZCeJEmSJIvGWOIq2K8URF/WYTCNQEGvcoF5zlJNkiRJkjZGFlf1o4r2ZaIN25hALZnmBoq2zchLkiRJkkViZHHVLk293ChF5urxdM9RS5fimiRJkiwaI4mrThdcu89//vM36Pqj6FoP1xodTpq/p8uFwn/tC3USSZKkHR2T1BoadaX5ySyg36wuT5pURE/aJEl+xUjiqn+pm0t3n3pagqbXj3jEI4rAKkrW7/ayyy4rrene9ra3dbbbbruV39W/dLfdduu8/vWvL31/B+l4kSTLxs9+9rMyoEIbO/fcrKDxvXmWOvucfvrp6w1QSJJkRHHVk1ErLG0EazQOd7OxRjU9r2ck6u+or2UTv0+EU1yTZSRGutVj3mrMFTXFw8/qHtnEzSP+Lp5n1Okt8Xz13/s6jq2JzlbmnmpyLrFRY/MkSX7FxOpcLQJ62GqqH9NEtNXi+tWLMSZw1DzoQQ8q4+LcmN3GpSXJIiKhT8a8/r+Qh2BQu2bptYiGaJl6U5eucRN//OMfL5tc4Znof2uSiaEUEg5PO+208j1CqOl6kze96U0r///IRz5SLFBDsk1NkWzo53qtev626TjuXw3N3dsprkmyPkOLK7E877zzNnADaYauOXLscsVjYjbij3/849bnktQUE26SZJkwN5X4hUWqsbppJUccccR64hrEDOPA0AGYL6kczr1kgotNKoE0ASiGEvAKcS8355m2TUch4hrW2ywbw4U//uM/Xhn1WEPgDccgwoR5jz32GOeUJMlCMbS4ivsY0N3GjTfeuDI31SQFu1677XkdtJskqwEPj7F3MBdSuCRmE9cTWszrjdFx3YYvSCiSXLjZZpt17na3u5WZvqZFsTaJocRBCYYmexDOtrGDZl6ahvM7v/M7RVAJ76GHHlpK5iRQ+V4MkW/iuKwJzSk7SbLsTMwtrONSDOU+7LDDOn/4h39YxjrZ9XILJ0nyS4x2MwqQCH7sYx8r4/EkAbI6Jf8FXLss017ojEZYazyf8Vnxf1x66aUrcdmanXbaqUzQqUdw2RArk4OZweZYSjzkcu4Ga5mbOEmSXzK0uBqs3CaWRx11VNlp//Vf/3XnhS984UQOLkkWFaLKUiR6XMH4zGc+UwaWf/CDH1yz47j73e9exLlbJjJXbwyJ7gW3cJIkv2JocVVC42Zs7qivvfbaDX5X3EezCbHX5tBmGOqMXXbZZdjDSJK5hquW63W//fbrnHDCCZ2nPe1pReDEUs8555xyn80TeQ8nyfqM5BYmlFdddVUR1BiyKxtR9qM+w9zDkphkQl599dWdrbbaqli1fl5nLUYsNrKLk2RZEBPlChZCkVjE8nvzm99cytckOhFXw98NNv/Od74z7cPtS97DSbI+I4mrbEJJFEceeeRKCYBkik996lOdRz7ykSsdlyRPSOnXSIIFK6swxFVSFAEW08ka12TZeMYznlEybcU2v/jFL3aOOeaYkqMgrOJegdinjSo3sY2okpomEVMFMV4tuj13JismSTsjievuu+9esgg//elPl123RQEPeMADWhMw7MKVCtQYVUegZUq2FaknySJDVCU12XAST3kK2ggS3TaEUN71rnetfK0VIp785CevfI9LWe3rLW5xi5Xv2exqV/rwhz985T5tQ006IT/uuOPK39RsueWWpR69iQ3BIYccUvIw/E6SJL9i5Gxh2YPcvepZ9Q4eFtavOrm/+qu/GvUQkmSu0azBppMrmFXatsmU9Ut8L7roopJdHCU5L33pSzf4Xe1Fm983tYpw8yLV4uq1rr/++pXvEVed1HiUfuM3fmPl92T9O876e8Hxxx9f/tUGtS2nIkmWmZHFlRtYRxn1c7vuuutQw9LteMVs/a2bOkmWFVZmbWk2kdPAmtU+VP5Ct3rXbgi5dHPpNr9PgJt1sO7PXvco65uAJ0myPiOLqxtOUsb+++/fueaaazpbb731wH9rd7xu3bpS75ckSXdYlkIvJ554Yslp0CZxFlABcP7555f48P3ud79pH06SzBxjNZHQpq1b55Ze6ErjkSRJf+5973tvMMZx2mh/qoQoSZJ2JtahKUmSJEmSX5LimiRJkiQTJsU1SZIkSSZMimuSJEmSTJj/B8Z+ePOXi14ZAAAAAElFTkSuQmCC"
}
},
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model for CFRP pullout test "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us construct another pullout model named `po_cfrp` with a bond slip law exhibiting strong softening. Such kind of behavior is observed in tests between FRP sheets and concrete. An example of such an experimental study \n",
"<a id=\"cfrp_trilinear_bond\"></a>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"po_cfrp = PullOutModel1D(n_e_x=300, w_max=0.8) # mm \n",
"po_cfrp.geometry.L_x=100 # mm\n",
"po_cfrp.time_line.step = 0.02\n",
"po_cfrp.cross_section.trait_set(A_m=400*200, A_f=100*0.11, P_b=100)\n",
"po_cfrp.material_model='trilinear'\n",
"po_cfrp.material_model_.trait_set(E_m=28000, E_f=230000, tau_1=5.5, tau_2=0, s_1=0.08, s_2=0.4)\n",
"po_cfrp.interact()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Conclusions:** to interactive study of CFRP sheet debonding\n",
" - The bond-slip law reported in the paper can reproduce well the pullout response measured in the test.\n",
" - The study of the debonding process shows that the adhesive is only active within an effective length of approximately 40-50 mm.\n",
" - As a consequence, in contrast to steel rebar studied above, the maximum pullout load cannot be increased by an increasing bond length.\n",
" - In the studied case there will FRP rupture is not possible because its strength is larger than $P_\\max$ of 25 kN. To verify this, we use the strength of 3550 MPa given in the above table and multiply with the cross-sectional area of the sheet, i.e. $f_t t_f p_b$ to obtain"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"f_t = 3550 # CFRP sheet strength in [MPa] - see the table above\n",
"f_t * t_f * p_b / 1000 # breaking force of the sheet 100 x 100 mm in [kN]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## **Question:** Effect of bond length on the pullout response - **bond softening**\n",
" - Similarly to the the example with bond hardening above, we ask the question what happens with the pullout curve if we reduce the bond length to a minimum. The answer is the same - we will recover a bond-slip law multiplied by the bond area.\n",
" - However, if we increase the bond length, the trend will be different as already mentioned above. Once the length exceeds the effective bond length, there will be no increase in the pullout force and the pullout curve will exhibit a plateau. Let us show this trend by running a simple parametric study. Instead of doing it step by step we now run a loop over the list of length and colors, change the parameter `geometry.L_x` within the loop, `reset`, `run`, and `plot` the pullout curve in a respective color. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/run.png\" alt=\"Run\" width=\"40\" height=\"40\">\n",
" <b>Run in a loop to see the effect of bond length</b> </div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that a list in python is defined by the brackets\n",
"```[1,2,3,4]```. Two lists can be \"zipped\" together so that we can run\n",
"a loop over the lengths and colors as shown in the third line of the cell\n",
"<a id=\"crfp_study\"></a>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, (ax, ax_bond_slip) = plt.subplots(1,2, figsize=(10,4), tight_layout=True)\n",
"fig.canvas.header_visible = False\n",
"for L, color in zip([5, 10, 50, 100, 200], ['red','green','blue','black','orange']):\n",
" print('evaluating pullout curve for L', L)\n",
" po_cfrp.geometry.L_x=L\n",
" po_cfrp.reset()\n",
" po_cfrp.run()\n",
" po_cfrp.history.plot_Pw(ax, color=color)\n",
"po_cfrp.material_model_.plot(ax_bond_slip)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# **Remark to structural ductility:** how to make the plateau useful?\n",
"\n",
"The softening bond cannot exploit the full strength of the CFRP sheet which might seem uneconomic at first sight. On the other hand it can be viewed as a mechanism that increases the deformation capacity of the structure with a constant level of load. This property can be effectively used to enhance the ductility of the structure, i.e. induce large deformation before the structural collapse required in engineering designs. This documents the importance of knowledge of the stress redistribution mechanisms available in the material. In steel reinforced structure, the ductility is provided inherently by the steel yielding property. In In case of brittle reinforcement, e.g. carbon fabrics, CFRP sheets, glass fabrics, other sources of ductility must be provided to ensure the sufficient deformation capacity between the serviceability and ultimate limit states. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/exercise.png\" alt=\"Run\" width=\"40\" height=\"40\">\n",
" <a href=\"../exercises/X0301 - Pull-out curve versus shear stress profiles.pdf\"><b>Exercise X0301:</b></a> <b>Pull-out curve versus shear stress profiles - part 1</b> \n",
"<a href=\"https://moodle.rwth-aachen.de/mod/page/view.php?id=551821\"><img src=\"../icons/bmcs_video.png\" alt=\"Run\"></a>\n",
"</div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left\"> <img src=\"../icons/exercise.png\" alt=\"Run\" width=\"40\" height=\"40\">\n",
" <a href=\"../exercises/X0302 - Pull-out curve versus shear stress profiles.pdf\"><b>Exercise X0302:</b></a> <b>Pull-out curve versus shear stress profiles - part 2</b> \n",
"<a href=\"https://moodle.rwth-aachen.de/mod/page/view.php?id=551823\"><img src=\"../icons/bmcs_video.png\" alt=\"Run\"></a>\n",
"</div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div style=\"background-color:lightgray;text-align:left;width:45%;display:inline-table;\"> <img src=\"../icons/previous.png\" alt=\"Previous trip\" width=\"50\" height=\"50\">\n",
" <a href=\"../tour2_constant_bond/fragmentation.ipynb#top\">2.3 Tensile behavior of composite</a> \n",
"</div><div style=\"background-color:lightgray;text-align:center;width:10%;display:inline-table;\"> <a href=\"#top\"><img src=\"../icons/compass.png\" alt=\"Compass\" width=\"50\" height=\"50\"></a></div><div style=\"background-color:lightgray;text-align:right;width:45%;display:inline-table;\"> \n",
" <a href=\"3_2_anchorage_length.ipynb#top\">3.2 Pullout curve versus bond length</a> <img src=\"../icons/next.png\" alt=\"Previous trip\" width=\"50\" height=\"50\"> </div> "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.8"
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": true,
"sideBar": true,
"skip_h1_title": true,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {
"height": "calc(100% - 180px)",
"left": "10px",
"top": "150px",
"width": "203.5px"
},
"toc_section_display": true,
"toc_window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 4
}